The table shows the age, in years, of employees in a company.
Age (a) in years Frequency
18 < a < 20
3
20 < a < 22
2
22 < a < 24
7
24 < a < 26
8
26
0
a) Find the modal class interval.
Isac
b) Work out an estimate of the mean age of these employees.
Answers
Answer:
a) The modal class for this case represent the class with the highest frequency
And for this case would be \( 24 <a<26\) with the highest frequency 8
b) \( \bar X = \frac{19*3 + 21*2 + 23*7 +25*8}{3+2+7+8} =23\)
Step-by-step explanation:
Part a
The modal class for this case represent the class with the highest frequency
And for this case would be \( 24 <a<26\) with the highest frequency 8
Part b
For this case we need to find the mid point of each interval:
Interval Midpoint Frequency
18-20 19 3
20-22 21 2
22-24 23 7
24-26 25 8
And we can find the sample mean with this formula:
\( \bar X = \frac{\sum_{i=1}^n f_i x_i}{n}\)
And replacing we got:
\( \bar X = \frac{19*3 + 21*2 + 23*7 +25*8}{3+2+7+8} =23\)
The class with the highest frequency represents the modal class for this case and for this case would be (24 < a < 26) with the highest frequency of 8 and an estimate of the mean age of these employees is 23.
Given :
The table shows the age, in years, of employees in a company.
A) The class with the highest frequency represents the modal class for this case and for this case would be (24 < a < 26) with the highest frequency 8.
B) To estimate the mean age of these employees, first, determine the midpoint.
Age Frequency Midpoint
18-20 3 19
20-22 2 21
22-24 7 23
24-26 8 25
The formula of the sample mean is given by:
\(\rm \bar{X} =\dfrac{\sum^{n}_{i=1}f_ix_i}{n}\)
\(\rm \bar{X} = \dfrac{19\times 3+21\times 2 +23\times 7+25\times 8}{3+2+7+8}\)
\(\rm \bar{X} = 23\)
For more information, refer to the link given below:
https://brainly.com/question/20747890
Related Questions
give an example of an infinite group that has both a subgroup isomorphic to d4 and a subgroup isomorphic to a4.
Answers
An infinite group is a group that has an infinite number of elements. An example of an infinite group with both a subgroup isomorphic to D4 and a subgroup isomorphic to A4 is the free product of the two groups. This is denoted as D4 * A4.
A group is called infinite if it is not finite. An infinite group is a group that has an infinite number of elements. An example of an infinite group with both a subgroup isomorphic to d4 and a subgroup isomorphic to a4 is the free product of the two groups. This is denoted as D4 * A4. Therefore, the free product of D4 and A4 is an infinite group with a subgroup isomorphic to D4 and a subgroup isomorphic to A4.
In algebra, a group is a mathematical object consisting of elements and an operation combining two elements to produce a third element. It satisfies axioms, including associativity, identity, and invertibility. A subgroup of a group is a subset of the group that forms a group under the same operation. Infinite groups are groups that are not finite. This means that they have an infinite number of elements.
They are often studied in algebra and topology. Infinite groups can be defined in various ways, including a limit of finite groups or a group with a countably infinite number of elements. D4 and A4 are both finite groups. D4 is the dihedral group of order 8, while A4 is the alternating group of order 12. D4 has eight elements, while A4 has twelve elements. Both groups are important in algebra and have been studied extensively.
A subgroup of a group is a subset of the group that forms a group under the same operation. A subgroup of a group isomorphic to another group is called an isomorphic subgroup. This means the two groups have the same structure, even though their elements may differ. An isomorphic subgroup of a group is often denoted using the symbol. Therefore, the free product of D4 and A4 is an infinite group with a subgroup isomorphic to D4 and a subgroup isomorphic to A4.
Therefore, an infinite group is a group that has an infinite number of elements. An example of an infinite group with both a subgroup isomorphic to D4 and a subgroup isomorphic to A4 is the free product of the two groups. This is denoted as D4 * A4.
To know more about the isomorphic subgroup, visit:
brainly.com/question/30907053
#SPJ11
Number of study sessions Total Enrollment
Morning class 25 16
Night class 20 22
If the total study sessions for the night class were proportional to the morning class, how many would you expect the night class to have? How does this compare to the actual amount of study session the night class has?
If the night class were proportional to the morning class, we would expect them to have
[ Select ]
[ Select ]
than the number of study sessions they have currently
Answers
If the total study sessions for the night class were proportional to the morning class that is 25: 20 then night class have the actual amount 80% students
we can calculate 20/25 *100
and we obtain the actual amount 80%
If the total study sessions for the night class were proportional to the morning class is 25: 20 and 16: 22
What is a proportion simple definition?
the size, number, or amount of one thing or group as compared to the size, number, or amount of another. the proportion of boys to girls in our class is three to one. : a balanced or pleasing arrangement
Initially, the number of lectures is 3 while the number of fieldwork is 12. Furthermore, the class sessions increased to 18 and the number of fieldwork remains the same (i.e. 12). Therefore, the number of lectures will be 18 - 12 = 6. The percentage of the sessions that were lectures will be:
(6/18)*100% = 33.3%
learn more about of amount here
https://brainly.com/question/13578110
#SPJ4
the gas tank in feliz car is 5/6 full
Answers
Answer:
Ok? what the question?
Step-by-step explanation:
Jughead now earns $10.50 per hour. This is 175% of what he earned last year. How much did he earn last year?
Answers
Answer:
10.5/175*100=6
Step-by-step explanation:
3
Period
Date
5. If a teacher were to distribute sheets of
paper so that each student got two
sheets, there would be 8 sheets
remaining. However, if three sheets
were given to each student, the teacher
would be 11 sheets short. Which
equation could be used to find how
many students are in the class?
Answers
If teacher is distributing sheets in a class, then the equation which is used to find number of students in class is (d) 2x+8 = 3x - 11.
A "Linear-Equation" is a mathematical equation that represents a straight line in a coordinate plane. It is of form : y = mx + b
where y is the dependent variable, x is the independent variable, m is the slope of the line, and b is the y-intercept (the point at which the line crosses the y-axis).
Let number of students in class be denotes as "x",
If each student get 2 sheets, then 8 sheets are remaining, it is mathematically represented as : 2x + 8 ,
If each student get 3 sheets each, then there would be 11 sheets less, and this is represented as : 3x - 11,
So, the equation which is used to find number of students in class is 2x+8=3x-11,
Therefore, the correct option is (d).
Learn more about Equation here
https://brainly.com/question/19626
#SPJ1
The given question is incomplete, the complete question is
If a teacher were to distribute sheets of paper so that each student got two sheets, there would be 8 sheets remaining. However, if three sheets were given to each student, the teacher would be 11 sheets short. Which equation could be used to find how many students are in the class?
(a) 2(x - 8) = 3(x + 11)
(b) 2(x + 8) = 3(x - 11)
(c) 2x-8 = 3x + 11
(d) 2x+8 = 3x - 11
Find the highest common factor of 12 and 40
Answers
To find the highest common factor (HCF) between two numbers , first to take HCF of both the numbers.
\( \purple {\Large\begin{array}{r | l}2&\underline{12}\\3& \underline{6}\\2&\underline{2}\\&\underline{1}\\\end{array}} \: \: \: \: \: \: \: \: \: \: \: \: \purple {\Large\begin{array}{r | l}2&\underline{40}\\2& \underline{20}\\5&\underline{10}\\2&\underline{2} \ \\ &\underline{1}\\\end{array}}\)
Take every common prime factor between 12 and 40\( \red {\large \implies} \large \: 12 \: = \: 2 \: \times \: 3 \: \times \: 2 \: \: \: \: \: \: \: \: \: \: \\ \\ \red {\large \implies} \large \:40 \: = \: 2 \: \times \: 2 \: \times \: 5 \: \times \: 2 \: \)
Finally, identify the factors common to each number and multiply those common factors together.
\( \rm\orange {\large \implies} \large \:Common \: factors \: = \: 2 \: \times \: 2\)
\(\rm\orange {\large \implies} \large \:HCF = 4\)
Hope this helps!
En la siguiente tabla se muestra la relación de 1100 piezas entre buenas y defectuosas elaboradas en un taller ceramista
Taza Plato jarrón total
Buena 830 85 1415
Defectuosa 10 5
Total 510 90
¿Cuál es la probabilidad de que se elija una pieza al azar y esté defectuosa dado que se sabe que es un plato?
¿Cuál es la probabilidad de que se elija una taza dado que esté defectuosa?
Answers
The probability that a piece selected at random and is defective given that it is known to be a plate is 0.0588 or 5.88%.
To calculate the probability, we need to use Bayes' theorem: P(defective|plate) = P(plate|defective) * P(defective) / P(plate).
P(plate|defective) = 5 / 25 = 0.2P(defective) = 25 / 1100 = 0.0227P(plate) = 90 / 1100 = 0.0818P(plate|defective) = 5 / 25 = 0.2P(defective) = 25 / 1100 = 0.0227P(plate) = 90 / 1100 = 0.0818Therefore, P(defective|plate) = 0.2 * 0.0227 / 0.0818 = 0.0588 or 5.88%.
The probability that a cup will be chosen given that it is defective is 0.4 or 40%.
To calculate the probability, we need to use the information given in the table:
Count the number of defective cups: 10Count the total number of defective products: 25Divide the number of defective cups by the total number of defective products: 10/25 = 0.4 or 40%.
Learn more about Probability:
https://brainly.com/question/24756209
#SPJ4
Complete Question:
The following table shows the relationship of 1100 pieces between good and defective made in a ceramic workshop
cup plate vase total
Good 830 85 1415
Defective 10 5
Overall 510 90
What is the probability that a piece is selected at random and is defective given that it is known to be a plate?
What is the probability that a cup will be chosen given that it is defective?
which of the following lines are parallel.
Lines a and b
lines a and c
Lines b and c

Answers
The lines which are parallel are none.
What is the slope?The slope is the ratio of the vertical changes to the horizontal changes between two points of the line.
m = ( y₂ - y₁ ) / ( x₂ - x₁ )
where (x₁, y₁) and (x₂, y₂) are the two points that you are trying to find the slope between.
Given;
Coordinates of three lines
a;(1,5) and (-2,-4)
b;(3,2) and (1,-4)
c;(6,1) and (-4,2)
Now, slopes of the lines
a= -4-5/-2-1
=10/3
b=-4-2/1-3
=-3
c=2-1/-4-6
=1/-10
Therefore, by slopes of the line none of them are parallel.
Learn more about slope here:
https://brainly.com/question/2503591
#SPJ1
In a right triangle , the longest side is 8 cm. One of the remaining sides is 4 root 3 cm long . find the length of the other side .
Answers
Answer:
The length of other side = 4 cm
Step-by-step explanation:
Given :
longest side = H = 8 cm
one side = P = 4√3
The other side will be H² = P² + B²
=> 8² = (4√3)² + B ²
=> 64 = 48 + B²
=> 64 - 48 = B²
=> 16 = B²
=> √16 = B
=> B = 4
Let the lengths of sides be a, b and c (hypotenuse).
Hypotenuse is the longest side , So c = 8.
\(\sf{Let \: b = 4\sqrt{3}}\)
From the pythagoras theorem :
\(a^2 + b^2= c^2\)
\(a^2 + (4\sqrt{3})^2= 8^2\)
\(a^2 + 16 (3) = 64\)
\(a^2 +48=64\)
\(a^2 = 16\)
\(a = 16 / 2\)
\(a = 4\)
The third side is 4 cm.
find the area of each figure

Answers
Answer:
9.6. 12. 25.4
Step-by-step explanation:
Find the area enclosed by the ellipse x2/a2 + y2/b2 = 1. SOLUTION Solving the equation of the ellipse for y, we get y2/b2 = 2 - x2/a2 = /a2 or y = plusmin b/a( ). Because the ellipse is symmetric with respect to both axes, the total area A is four times the area in the first quadrant (see the figure). The part of the ellipse in the first quadrant is given by this function. y = b/a( ) 0 le x le a and so 1/4A = int a 0 b/a( )dx. To evaluate this integral we substitute x = a sin theta. Then dx = d theta. To change the limits of integration we note that when x = 0, sin theta = 0, so theta = 0; when x = a, sin theta = 1, so theta = . Also since 0 le theta le pi/2. therefore We have shown that the area of an ellipse with semiaxes a and b is pi ab. In particular, taking a = b = r, we have proved the famous formula that the area of a circle with r is pi r2.
Answers
The area enclosed by the ellipse with equation x^2/a^2 + y^2/b^2 = 1 is given by the formula pi * a * b. This formula applies to ellipses with semi-axes a and b. The proof involves solving the equation for y and obtaining the equation of the ellipse in the first quadrant.
To find the area enclosed by the ellipse x²/a² + y²/b² = 1, we begin by solving the equation for y. This gives us y²/b² = 2 - x²/a² or y = ± (b/a)√(a² - x²). Since the ellipse is symmetric with respect to both axes, the total area A is four times the area in the first quadrant.
In the first quadrant, the equation of the ellipse becomes:
y = (b/a)√(a² - x²) for 0 ≤ x ≤ a.
To determine the area, we integrate this equation with respect to x over the interval [0, a]. Substituting x = a sinθ and differentiating, we find dx = a cosθ dθ.
By changing the limits of integration, we note that when x = 0, sinθ = 0, so θ = 0; and when x = a, sinθ = 1, so θ = π/2. Thus, the integral becomes 1/4A = ∫[0,π/2] (b/a)(a cosθ)(a dθ).
Simplifying, we have 1/4A = (b/a) * a² ∫[0,π/2] cosθ dθ. The integral of cosθ over [0,π/2] is sinθ evaluated at the limits, which gives:
sin(π/2) - sin(0) = 1 - 0 = 1.
Therefore, we have 1/4A = (b/a) * a² * 1, which simplifies to 1/4A = a * b. Multiplying both sides by 4, we get A = π * a * b, which proves that the area of an ellipse with semi-axes a and b is given by the formula π * a * b.
In particular, when the ellipse is a circle with radius r, we can substitute a = b = r, yielding A = π * r^2. Thus, we have proven the well-known formula for the area of a circle.
Learn more about Ellipse:
brainly.com/question/20393030
#SPJ11
consider two positive even integers less than $15$ (not necessarily distinct). when the sum of these two numbers is added to their product, how many different possible values may result?
Answers
The problem asks for the number of different possible values that can result from adding the sum and product of two positive even integers less than 15.
To find the possible values, we consider all pairs of positive even integers less than 15. Since both numbers must be even, they can be expressed as 2k and 2m, where k and m are positive integers. The sum of these two numbers is 2k + 2m = 2(k + m), and their product is (2k)(2m) = 4km.
Considering the constraints, k and m can take values from 1 to 7, as the maximum even integer less than 15 is 14. By substituting different values of k and m, we can generate different values of the sum and product.
To count the different possible values, we observe that the value of 2(k + m) depends on the sum of k and m, while the value of 4km depends on their product. As there are 7 possible values for the sum (k + m) and 7 possible values for the product km, we multiply these two counts to obtain the total number of different possible values.
Hence, the number of different possible values resulting from adding the sum and product of two positive even integers less than 15 is 7 * 7 = 49.
To know more about integers click here: brainly.com/question/490943
#SPJ11
Substitute the values for the base and the height into the area formula.
What is the area of the triangle?
The area of the triangle is _____square inches.
PLS HELP!! I WILL GIVE BRAINLYIST!!!

Answers
Answer:
A= 60
Step-by-step explanation:
A = ab/2 where a and b are legs of the triangle.
First we substitute:
A = 12 x 10 / 2
Then we solve (you can plug it in the calculator):
A= 120 / 2
A= 60
A triangle has angle measures of (x + 3)º, (5x − 8)º, and (2x + 1)º. - What is the measure of the smallest angle of the triangle in degrees? A 47° B C 26° 107⁰ 23°

Answers
I think the the answer is b Answer:
Step-by-step explanation:
40 POINTS PLEASE HELP!!!!!!!!

Answers
Answer:
I belive that your answer would be Spinner B. I may be wrong.
5 x 5^2 leaving answer in index notation
Answers
In multiplication, the exponents add up.
5.5²=5¹.5²=5³
Note:
In the extraction ,the exponents remove.
5¹⁰÷5³=5⁷
Answer:
5³
Step-by-step explanation:
Using the rule of exponents
\(a^{m}\) × \(a^{n}\) = \(a^{(m+n)}\)
Given
5 × 5²
= \(5^{1}\) × 5²
= \(5^{(1+2)}\)
= 5³ ← in index form
= [ 125 ]
Find the least number which when divisible by 20, 24, 32 and 38 leaves a remainder 5 in cach case
Answers
Answer:
18245
Step-by-step explanation:
We have to use L.C.M,
L.C.M(20,24,32,38)
2|20,24,32,38
2| 10 ,12 ,16 ,19
2| 5 , 6 , 8 , 19
2| 5 , 3 , 4 , 19
2| 5 , 3 , 2 , 19
L.C.M = 2 x 2 x 2 x 2 x 2 x 2 x 5 x 3 x 19
= 18240
Now for each case remainder is 5,
So the number is 18240+5
=> 18245
what is -0.10416666666 as a fraction
Answers
Answer:-5208333333/50000000000
Step-by-step explanation:
Solve the inequality
6x-2(x+2)>0
Answers
Answer:
its 0
Step-by-step explanation:
6x^(2)+x-2=0
On the last day of school, Kendrick wants to bring in homemade breakfast biscuits for his classmates. He makes a batch of 25 biscuits using 8 cups of flour. How much flour is in each biscuit?
Answers
Answer:
0.32 Cups of flour.
Step-by-step explanation:
Since He made a batch of 25 biscuits using 8 cups of flour, then each biscuit contain 8/25 Cups of flour.
In each biscuit, there are 8/25 cups of Flour.
What are mathematical operations?The term "operation" in mathematics refers to the process of computing a value utilizing operands and a math operator. For the specified operands or integers, the math operator's symbol has predetermined rules that must be followed. In mathematics, there are five basic operations: addition, subtraction, multiplication, division, and modular forms.
Given, On the last day of school, Kendrick wants to bring in homemade breakfast biscuits for his classmates.
Since,
He makes a batch of 25 biscuits using 8 cups of flour.
So,
For 25 biscuits, it required flour = 8 cups
Thus, from the proportionality
For 1 biscuit, it required flour = 8/25 cups
Therefore, there are 8/25 cups of flour is in each biscuit.
Learn more about Mathematical operations here:
https://brainly.com/question/20628271
#SPJ2
For the following distribution; what is the highest score? [2 pts] 20-25 15-19 10-14 5-9 4) a) 22 b) 20 c) 25 d) Cannot be determined
Answers
The highest score for the given distribution is 25.
This is because the distribution is divided into ranges, with the first range being 20-25, the second range being 15-19, the third range being 10-14, and the fourth range being 5-9.
The highest score in each range is the number on the right side of the dash.
Therefore, the highest score in the first range is 25, the highest score in the second range is 19, the highest score in the third range is 14, and the highest score in the fourth range is 9.
Since 25 is the highest score among all of the ranges, it is the highest score for the entire distribution.
The correct answer is c) 25.
Read more about distribution ranges at:
https://brainly.com/question/16237757
#SPJ11
Write the equation of a line that passes through the given point and is parallel to the given line. Write the equation in slope-intercept form (5,2); x + y = 12
Answers
The equation of a line parallel to the line x + y = 12 and passing through the point (5, 2) can be expressed in slope-intercept form as y = -x + 7.
To find the equation of a line parallel to the given line x + y = 12, we need to determine its slope. The given equation can be rearranged into the slope-intercept form y = -x + 12 by subtracting x from both sides. From this form, we can see that the slope of the line is -1.
Since parallel lines have the same slope, the parallel line we seek will also have a slope of -1. Now, we can use the point-slope form of a linear equation to find the equation of the line passing through the point (5, 2). The point-slope form is given by y - y1 = m(x - x1), where (x1, y1) is a point on the line and m is the slope.
Substituting the values of (5, 2) for (x1, y1) and -1 for m, we get y - 2 = -1(x - 5). Simplifying this equation, we have y - 2 = -x + 5. Rearranging it to the slope-intercept form, we find y = -x + 7, which is the equation of the line parallel to x + y = 12 and passing through the point (5, 2).
Learn more about slope here: https://brainly.com/question/29184253
#SPJ11
i need help on 7, 9, 10

Answers
31.626
9)
140.55
10)
48.42
Solve the equation. Round to the nearest tenth if necessary. 196=n^2
Answers
Answer:
10
Step-by-step explanation:
The pair of equations y = 0 and y = -7 has how many solutions?
Answers
Answer:
2 solutions so it can be inferred that it might be a quadratic
Step-by-step explanation:
Answer:
no solutions
Step-by-step explanation:
y = 0 and y = - 7 are horizontal parallel lines.
Since they are parallel, they never intersect and so have no solutions.
A gas pipe company is laying gas pipe through some mountains. Due to the uneven landscape, the workers must lay approximately 5,500 feet of pipe for every mile of land they cover. If the workers must cover 7 miles through the mountains, how many feet of pipe will they need?
Answers
The number of feet of pipes they will need to cover 7 miles through the mountains is 38,500 feet
Given:
Length of pipe per mile = 5,500 feet
Ratio of pipe to mile = 5,500 : 1
find pipes needed for 7 miles
let x = number of pipes
Ratio of pipe to mile = x : 7
Equate both ratio
5,500 : 1 = x : 7
5,500/1 = x/7
cross product
5,500 × 7 = 1 × x
38,500 feet = x
Therefore, the number of feet of pipes they will need to cover 7 miles through the mountains is 38,500 feet
Learn more about ratio:
https://brainly.com/question/21602143
Angelina’s family owns a mini-golf course. When discussing the business with a customer, she explains there is a relationship between the number of visitors and hole-in-one winners. If x is the number of visitors and y is the number of winners, which conclusion is correct?
The ordered pair (–3, 6) is viable.
The ordered pair (7, 2) is viable.
The ordered pair (15, –7) is viable.
The ordered pair (18, 3) is non-viable.
Answers
Answer:
look at the image and give me brainliest k thx
Step-by-step explanation:

Answer:
Step-by-step explanation:
7,2 is viable
Plz answer I need help my teacher doesn't explain things good
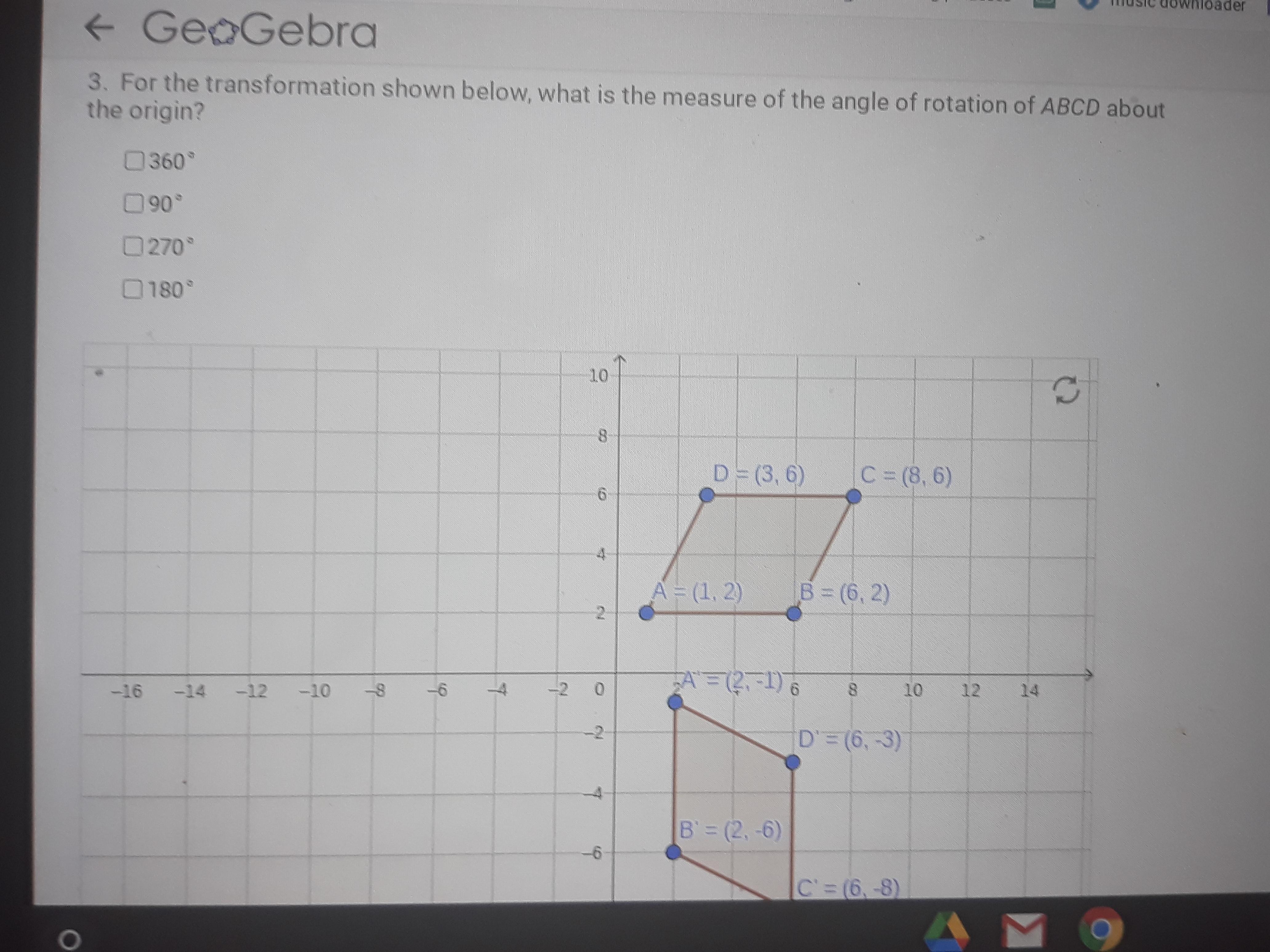
Answers
Select the answer with the correct number of decimal places for the following sum.
13.914 cm + 243.1 cm + 12.00460 cm = _____
a. 269.01860 cm
b. 269.02 cm
c. 269.0186 cm
d. 269.0 cm
e. 269.019 cm
Answers
Answer:
269.01860??
But i can tell u 13.914 cm + 243.1 cm + 12.00460 cm = 260.01860 not 269.01860
Step-by-step explanation:
A DVD has a diameter of 18 centimeters. What is the area of the DVD? Round your answer to the nearest hundredth. Use 3.14 for π.
Answers
Answer:
. SAME THING YOU PUT FOR MY ANSWER IM GONNA DO THE SAME FOR YOU
Step-by-step explanation: