The sum of 3 consecutive even numbers is 72 what is the smallest of the three numbers
Answers
Answer:
23
Step-by-step explanation:
x + (x + 1) + (x + 2) = 72
3x + 3 = 72
3x = 69
x = 23
check answer:
23 + 24 + 25 = 72
Related Questions
A hiker walks 11 km due north from camp and then turns and walks 11 km due east. What is the angle of the displacement (on a straight line) of the
hiker from the camp?
Answers
Answer:
45°
Step-by-step explanation:
If you walk forwards, and make a 90° turn and walk the same amount, the angle will be half of 90, which is 45.
f(x) = 3(x-4)2-2
Pls help me solve
Answers
Answer:
x = 13/3
Step-by-step explanation:
Solve for x:
3×2 (x - 4) - 2 = 0
Hint: | Multiply 3 and 2 together.
3×2 = 6:
6 (x - 4) - 2 = 0
Hint: | Distribute 6 over x - 4.
6 (x - 4) = 6 x - 24:
6 x - 24 - 2 = 0
Hint: | Group like terms in 6 x - 24 - 2.
Grouping like terms, 6 x - 24 - 2 = 6 x + (-24 - 2):
6 x + (-24 - 2) = 0
Hint: | Evaluate -24 - 2.
-24 - 2 = -26:
6 x + -26 = 0
Hint: | Isolate terms with x to the left hand side.
Add 26 to both sides:
6 x + (26 - 26) = 26
Hint: | Look for the difference of two identical terms.
26 - 26 = 0:
6 x = 26
Hint: | Divide both sides by a constant to simplify the equation.
Divide both sides of 6 x = 26 by 6:
(6 x)/6 = 26/6
Hint: | Any nonzero number divided by itself is one.
6/6 = 1:
x = 26/6
Hint: | Reduce 26/6 to lowest terms. Start by finding the GCD of 26 and 6.
The gcd of 26 and 6 is 2, so 26/6 = (2×13)/(2×3) = 2/2×13/3 = 13/3:
Answer:x = 13/3
find the general solution of the given differential equation. y'' − y' − 2y = −6t 10t^2. y(t) = ?
Answers
Set the right-hand side equal to zero to obtain the related homogeneous equation:
y'' − y' − 2y = 0
r2 - r - 2 = 0 is the characteristic equation.
The result of factoring this equation is (r - 2)(r + 1) = 0
The roots are therefore r = 2 and r = -1.
The homogeneous equation's general solution is the following:
y_h(t) equals c1*e(2t) plus c2*e(-t).
We need to identify a specific solution in order to discover the nonhomogeneous equation's general solution. The approach of indeterminate coefficients can be used to infer a form for a specific solution. We can speculate on a specific solution of the following kind because the polynomial on the right-hand side of the equation is of degree 2.
At2 + Bt + C = y_p(t)
Taking y_p(t)'s first and second derivatives, we obtain:
y_p'(t) equals 2At + B
y_p''(t) = 2A
When these expressions are substituted into the initial differential equation, we obtain:
-6t + 10t2 = 2A - (2At + B) - 2(At2 + Bt + C)
When we condense and group related terms, we get:
-6t + 10t2 = (-2A)t2 + (-2B-2A)t + (2A-B-2C)t
When like terms' coefficients are equated, we obtain:
-2A = 10, -2B - 2A = -6, 2A - B - 2C = 0
If we solve for A, B, and C, we obtain:
A = -5, B = 4, C = -11/4
The specific solution is thus:
y_p(t) = -5t^2 + 4t - 11/4
As a result, the following is the nonhomogeneous equation's general solution:
c1*e(2t) + c2*e(-t) - 5t2 + 4t - 11/4 are equivalent to y(t) = y_h(t) + y_p(t).
where the initial circumstances define the constants c1 and c2.
To know more about differential equation refer here:
https://brainly.com/question/25731911?#
SPJ11
use the result from part (a) to find a series representation for the function f(x) =
Answers
∑xn=11−x
when x
is in the radius of convergence
∑(−x)n=11+x∑(−x2)n=∑(−1)nx2n=11+x2∑(−1)n(2–√x)2n=∑(−1)n(2n)x2n11+2x2x∑(−1)n(2n)x2n=x1+2x2∑(−1)n(2n)x2n+1=x1+2x2
The series convenes by the root test if:
limn→∞|an−−√nx|<1
|an−−√n|=|2n2n+1x|<1
|x|<2√2
Learn more about the Series here:
https://brainly.com/question/30457228
#SPJ1
please help it would be greatly appreciated:)

Answers
Hi, so I know the answer to this problem (now that I got it wrong) but I'm not quite sure why I was wrong, help?

Answers
Answer:
\(-2x^2-x\). Your answer was wrong because "x-squared" terms didn't cancel.
Step-by-step explanation:
To solve this problem, set up an equation. We know something is supposed to be added to the expression \(2x^2+2x\), and the result should be x. So:
\(2x^2+2x+(\text{ ? })=x\)
We want to solve for the question mark... the unknown thing that we're adding to the original expression, in order to get x.
It is uncommon to put question marks in equations to represent quantities. Usually we use a letter. Since x is already being used in the equation, we should pick something else ... we could use "y".
\(2x^2+2x+(\text{ } y \text{ })=x\)
...or just...
\(2x^2+2x+y=x\)
Algebra allows us to solve the equation and find out what "y" is equivalent to.
To solve, we want to get the "y" by itself. To do so, we try to eliminate the other "terms" from the left side of the equation.
Understanding "terms" & "like terms"
Terms
"Terms" in an equation are either a number multiplied to other things, or just a single number that isn't multiplied to anything else.
For example, the various terms in our equation above are
\(2x^2\), \(2x\), \(y\), \(x\)
You might ask why the last things, which don't have a number, are considered terms.
Remember that multiplying by 1 doesn't change anything, so we could imagine each of the last two terms as being 1 times the letter.
So, we can rewrite our equation:
\(2x^2+2x+1y=1x\)
Like terms
"Like terms" are terms where the "other stuff the numbers are multiplied to" is the same, so for instance, the \(2x\) and the \(1x\) are like terms. They are like terms because, the "other stuff" that the numbers are multiplied to are "x" for both terms. Note that \(2x\) and \(2x^2\) are not "like terms" because the "stuff" is different:
\(x\) is different than \(x^2\)
"Like terms" are important because only like terms can be "combined" into a single simplified term.
Solving equations
To solve an equation, we isolate what we're solving for, y, by disconnecting the other terms from it, and simplify.
Starting with subtracting 2x from both sides of the equation:
\(2x^2+2x+1y=1x\\(2x^2+2x+1y)-2x=(1x)-2x\)
Subtraction is the same as "adding a negative":
\(2x^2+2x+1y+(-2x)=1x+(-2x)\)
Since all terms are now connected by addition, we can add in any order we want (because of the Commutative Property of Addition), and we can combine like terms.
Thinking just about the number parts, since \(1+(-2)=-1\), then \(1x+(-2x)=-1x\).
Returning to our main equation, the right side simplifies:
\(2x^2+2x+1y+(-2x)=1x+(-2x)\\2x^2+2x+1y+(-2x)=-1x\)
On the left side: \(2x\) and \(-2x\) are like terms.
Fact: \(2+(-2)=0\)
So, \(2x+(-2x)=0x\)
Since anything times zero is just zero, \(0x=0\). Furthermore, adding zero to anything doesn't change it. So when the \(2x\) and \(-2x\) terms on the left side of our main equation are combined, they "disappear" (While we talked through are a lot of rules/steps to justify why that works, it is common to omit those justifications, and to just combine those like terms and make them disappear.)
So, \(2x^2+2x+1y+(-2x)=-1x\) simplifies to:
\(2x^2+1y=-1x\)
Similarly for the \(2x^2\) term, we subtract from both sides:
\(2x^2+1y=-1x\\(2x^2+1y)-2x^2=(-1x)-2x^2\\2x^2+1y+(-2x^2)=-1x+(-2x^2)\)
Combining like terms on the left, they disappear.
\(1y=-1x+(-2x^2)\)
There are no like terms on the right.
Since the two terms on the right are added together, we can use the commutative property of addition to rearrange:
\(1y=-2x^2+(-1x)\)
Addition of a negative can turn back into subtraction, and simplify multiplication by 1.
\(y=-2x^2-x\)
Remembering we chose "y" as the unknown thing we wanted to know, that's why the "correct answer" is what it is.
Verifying an answer
Verifying can double check an answer, and helps explain why the answer you chose doesn't work.
To verify an answer, the original statement said add something to the expression and get a result of "x". So, let's see if the "correct answer" does:
\(2x^2+2x+(\text{ } ? \text{ })\\2x^2+2x+(-2x^2-x)\\2x^2+2x+(-2x^2-1x)\\2x^2+2x+(-2x^2)+(-1x)\)
Combining the "x-squared" terms, completely cancels...
\(2x+(-1x)\)
Combining the "x" terms, and simplifying...
\(1x\\x\)
So it works.
Why isn't the answer what you chose:
\(2x^2+2x+(\text{ } ? \text{ })\\2x^2+2x+(-x^2-x)\\2x^2+2x+(-1x^2-1x)\\2x^2+2x+(-1x^2)+(-1x)\)
Combining the x-squared terms, things don't completely cancel...
\(1x^2+2x+(-1x)\)
Combining the x terms...
\(1x^2+1x\\x^2+x\)
So adding the answer that you chose to the expression would not give a result of "x", which is why it is "wrong"
-5x-4y=10
y intersect: (____ ; ____)
x intersect: (____; _____)
see picture above. dont answer if u dont know. first gets marked brainliest!!

Answers
Answer:
y intercept = \((0, ~-\frac{5}{2} )\)
x intercept = \((-2, ~0)\)
.
Step-by-step explanation:
\(-5x - 5y = 10\)
.
y intercept
\(\to x = 0\)
\(-5(0) - 4y = 10\)
\(-4y = 10\)
\(y = \frac{10}{-4}\)
\(y = -\frac{5}{2}\)
so, the answer is \((0, ~-\frac{5}{2} )\)
.
x intercept
\(\to y = 0\)
\(-5x - 4(0) = 10\)
\(-5x = 10\)
\(x = \frac{10}{-5}\)
\(x = -2\)
so, the answer is \((-2, ~0)\)
.
Happy to help :)
Answer:
wjwjwjwjwj qjqjjw ajajwj ajajqjjq qjqjaj wjwjjw wjwjwj wjwjw
Step-by-step explanation:
bqhhq wjwjw wjwjw wjwj
Select the correct answer from the drop-down menu Central angle BACof circle Ameasures Tradians. Arc BChas a length of 63.48 centimeters. What is the radius of the circle? The radius of circle Ais 110.4 55.2 993.6 207 20 centimeters. Reset Next
Answers
If Central angle BAC of circle A measures 23/20 π T radians. Arc BC has a length of 63.48 centimeters. The radius of the circle A is: 55.2cm.
How to find the radius of circle A?In this case, we know the length of arc BC is 63.48 cm and the central angle BAC measures 23/20 π radians.
Now let find the radius of circle A:
So:
63.48π = (23/20 π)/2π × 2πr
63.48π = 1.15 rπ
Divide both side by 1.15
r = 63.48 /1.15
r =55.2 cm
Therefore we can conclude that the radius of circle A is approximately 55.2 centimeters.
Learn more about radius here:https://brainly.com/question/27696929
#SPJ1
The complete question is:
Central angle BAC of circle A measures 23/20 π T radians. Arc BC has a length of 63.48 centimeters. What is the radius of the circle? The radius of circle A is
Consider "Since some shoes are sneakers, some non-sneakers are non-shoes." This inference, drawn by contraposition, is:
A) Valid
B) Not valid
C) Valid by limitation
Answers
The correct option is B) Not valid. Consider the statement “Since some shoes are sneakers, some non-sneakers are non-shoes.”
We know that all sneakers are shoes, but all shoes are not sneakers. Hence, some shoes are sneakers. But, this statement does not imply that “some non-sneakers are non-shoes.” This inference cannot be drawn by contraposition. So, it is not valid.Inferences cannot be drawn in contraposition all the time. Contraposition is a type of logical statement that involves reversing and negating the terms of an original proposition. It is a logical relationship between a proposition and its converse. If a proposition is true, the contrapositive is always true.An example of contraposition can be shown as follows:“If a person is a human, then they are mortal.”We can write the contrapositive of this statement as:“If a person is not mortal, then they are not human.”
To know more about contraposition visit:
https://brainly.com/question/18120338
#SPJ11
What’s the function?

Answers
Volume of a cone rh, curved surface area of a cone = xr!] [Volume of a spheresurface area of a sphere 4ar']
The solid is formed from a hemisphere of radius rcm fixed to a cone of radius rcm and height hem. The volume of the hemisphere is one third of the volume of the solid.
(a) Find h in terms of r
(b) The slant height of the cone can be written as Vk cm, where k is an integer.
Find the value of k
(c) Find an expressionin terms of r and x, for the total surface area, in cm², of the solid
Answers
Answer:
Long solution
Step-by-step explanation:
(a) Let the height of the cone be h cm. The volume of the hemisphere is given by (1/2)(4/3)πr³ = (2/3)πr³. The volume of the solid is the sum of the volumes of the hemisphere and the cone, which is (2/3)πr³ + (1/3)πr²h. Since the volume of the hemisphere is one third of the volume of the solid, we have:
(2/3)πr³ = (1/3)πr²h
Simplifying, we get:
2r = h
Therefore, h is expressed in terms of r as h = 2r.
(b) The slant height of the cone can be found using the Pythagorean theorem. Let l be the slant height, then we have:
l² = r² + h²
Substituting h = 2r, we get:
l² = r² + (2r)² = 5r²
Taking the square root of both sides, we get:
l = r√5
Since k is an integer, we can write:
l = Vk cm, where k is an integer
Comparing the two expressions, we get:
Vk = r√5
Therefore, the value of k is k = ⌊r√5⌋, where ⌊x⌋ denotes the largest integer less than or equal to x.
(c) The total surface area of the solid is the sum of the curved surface area of the cone, the curved surface area of the hemisphere, and the area of the circular base of the cone. We have:
Curved surface area of the cone = πr l = πr(r√5) = πr²√5
Curved surface area of the hemisphere = 2πr²
Area of the circular base of the cone = πr²
Therefore, the total surface area of the solid, in cm², is given by:
πr²√5 + 2πr² + πr² = (πr²)(√5 + 3)
Find the speed of the object whose position function is given by F(t) = (7t² + 4, 4t − 2, t³ + 4t) at t = 4 Please show your answer to at least 4 decimal places. Speed =
Answers
At t = 4, the object has a speed of approximately 34.5506 units per second, calculated by finding the magnitude of its velocity vector.
To find the speed of the object, we need to calculate the magnitude of its velocity vector. The velocity vector is the derivative of the position function with respect to time. Given the position function F(t) = (7t² + 4, 4t − 2, t³ + 4t), we can differentiate each component with respect to time to obtain the velocity vector.
Taking the derivatives, we have:
F'(t) = (14t, 4, 3t² + 4)
Now, substitute t = 4 into the velocity vector to get the velocity at that particular time:
F'(4) = (14(4), 4, 3(4)² + 4)
= (56, 4, 52)
The magnitude of the velocity vector can be calculated using the formula:
Speed = ||F'(4)|| = √(56² + 4² + 52²) ≈ 34.5506
Therefore, the speed of the object at t = 4 is approximately 34.5506.
Learn more about Speed
brainly.com/question/17661499
#SPJ11
The graph shows the cost (C) of shipping a package based on its mass in pounds (p)
Enter an equation to represent the cost (C) of shipping a package based on its mass in pounds (p).

Answers
Answer:
C = 4p
Step-by-step explanation:
Because it starts at 0 pounds costs 0 dollars, we know it starts at the origin and has no y-intercept. Because it rises up 20 dollars for every 5 pounds, we can use rise/run to do 20/5 to get an increase of 4 dollars per pound.
Help me Please
i need to know the exact answer
I don't need to know how to solve thanks :)

Answers
Answer:
SA= 119 cm²
Step-by-step explanation:
the solution contain of four steps
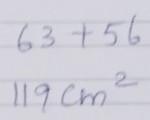
A bag contains 20 coloured marbles. Copy and
complete the table below to show the probability of
picking each colour at random and the number of
each colour marble in the bag. What is the
probability, as a percentage (%), of picking a purple
marble at random? How many purple marbles are in
the bag?
Colour
Yellow
Blue
Green
Purple
Probability
10%
15%
Number of marbles
6

Answers
Blue Probability = 30 %
Green No. of balls = 3
Purple Probability = 45 %
Purple No. of balls = 9
For f(x) = 2x + 1 and g(x) = 2
7, find (f- g)(x)
Answers
The value of (f- g)(x) is 2x - 26.
This is a question of subtraction of functions.
Subtraction of functions
The subtraction of function involves the creation of a new function through the addition of two other functions.
Subtraction of one real-valued function from another.
Let h: X → and p: X → be any two real functions, where X ⊆ Real numbers. Then, we can define h - p: X → by h - p x = h(x) – p(x), for all x ∈ X.
Given that:-
f(x) = 2x + 1
g(x) = 27
We have to find the value of (f- g)(x)
We know that,
(f- g)(x) = f(x) - g(x)
Hence, we can write,
(f- g)(x) = 2x + 1 - 27 = 2x - 26
To learn more about subtraction of functions, here:-
https://brainly.com/question/14630324
#SPJ1
How Many Cups In A Pound?
Answers
One pound is equal to approximately 2 cups.
It's important to note that this conversion is an approximation and may not be exact, especially if you are measuring ingredients like flour or sugar, which can be packed differently.
To ensure accurate measurements, it's best to use a kitchen scale to measure ingredients by weight.
In conclusion, 1 pound is approximately equal to 2 cups. When converting between pounds and cups, it's important to keep in mind that this conversion may not be exact, especially when measuring ingredients like flour or sugar.
to know more about cups in pound refer here
https://brainly.com/question/13947362#
#SPJ11
Bethany thinks of a number 6/13 of her number is 48 what is 1/13
Answers
The number that Bethany thinks of is 104, and 1/13 of that number is 8.
Word problemsWord problems in mathematics involve arithmetic operations and the use of variables to solve those problems. Word problems are problems we encounter in our daily life and with the use of correct mathematical interpretation, we can provide accurate solutions to them.
Let the number that Bethany thinks of be (x) for example. So, 6/13 of x is equal to 48.
i.e.
(6/13) * (x) = 48
By dividing both sides with (6/13), we have:
x = 48 ÷ (6/13)
x = 48 × (13/6)
x = 8 × 13
x = 104
Thus, 6/13 of the number that Bethany thinks of that gives us 48 is 104. Now, to find 1/13 of 104, we have:
1/13 × 104
= 8
Learn more about word problems in mathematics here:
https://brainly.com/question/21405634
#SPJ1
Mary Ellen saves 15% of each of her paychecks for her college fund. If Mary Ellen saved $60 from her last paycheck, how much was she paid?
Answers
Answer:
$400
..................
Given the vectors P= (11)i + (10)j + (11)k. Q = (3)i + (4)j - (5)k, and S =-4i + j-2k, compute the scalar products P.Q, P.S, and Q.S. The scalar product for P-Q, P-S, and Q.
Answers
The scalar product P.Q = 33, P.S = -25, and Q.S = -2. The scalar product P-Q, P-S, and Q-S are not defined.
The scalar product, also known as the dot product, is a mathematical operation that takes two vectors and returns a scalar quantity. To compute the scalar product of two vectors, we multiply their corresponding components and sum the results.
For the given vectors, P = (11)i + (10)j + (11)k, Q = (3)i + (4)j - (5)k, and S = -4i + j - 2k.
To find P.Q, we multiply the corresponding components of P and Q and sum the results: P.Q = (11)(3) + (10)(4) + (11)(-5) = 33.
Similarly, P.S = (11)(-4) + (10)(1) + (11)(-2) = -25, and Q.S = (3)(-4) + (4)(1) + (-5)(-2) = -2.
However, the scalar product P-Q, P-S, and Q-S are not defined since these operations involve subtracting vectors, and the scalar product is not defined for vector subtraction.
Therefore, the scalar products P.Q = 33, P.S = -25, and Q.S = -2, while the scalar products P-Q, P-S, and Q-S are not defined.
To learn more about mathematical operation click here
brainly.com/question/12809457
#SPJ11
i don't understand this math please anyone help

Answers
Consider the following current information for Galaxy Inc::
Output = 200 units
ATC = $50
What is the total cost of producing 200 units of output?
a. $10,000
b. $8,000
c. $1,100
d. Non
Answers
The answer is (a) $10,000.
How the total cost of producing 200 units of output can be found?The total cost of producing 200 units of output can be found by multiplying the output (200 units) by the average total cost (ATC) per unit, which is given as $50. Therefore, the total cost is:
Total Cost = Output x ATC
Total Cost = 200 x $50
Total Cost = $10,000
Therefore, the answer is (a) $10,000.
Learn more about average
brainly.com/question/24057012
#SPJ11
Scott likes to run long distances. He can run 20 km, end text in 85 minutes. He wants to know how many minutes (m) it will take him to run 52 km, How long will it take Scott to run 52 km?
Answers
Answer:221 min
Step-by-step explanation:
Given
Scott run 20 km in 85 minutes
Speed is given by
\(\Rightarrow \text{speed}=\dfrac{\text{distance}}{\text{time}}\)
Speed of Scott
\(\Rightarrow v=\dfrac{20}{\frac{85}{60}}=\dfrac{20\times 60}{85}=14.117\ km/hr\)
For 52 km, time taken is
\(\Rightarrow \text{time t}=\frac{52}{14.117}=3.683\ hr\ or\\\Rightarrow t=221\ min\)
Create two groups of cards with the SAME SUM using as many cards as possible using the numbers 1 -4 -2 2 8 5
Answers
Group 1: [1, 4, 5, 8] (sum=18)
Group 2: [-2, -2, 2, 2] (sum=0)
Another possible solution:
Group 1: [1, 4, 2, 5, 2] (sum=14)
Group 2: [-2, -2, 8] (sum=6)
How many unique ways are there to arrange the letters in the word PRIOR
Answers
Answer:
60
Step-by-step explanation:
based on my previous learning.. hope it helps.. correct me if im wrong..
PLEASE HELP MARKING BRAINLEIST JUST ANSWER ASAP AND BE CORRECT

Answers
Answer:
4t - 22
Step-by-step explanation:
To find:-
Perimeter of the given figure.Answer:-
To find out the perimeter we can simply add all the side lengths of the given figure. Since the given figure here is a rectangle, we can add up all the four sides to find the perimeter.
The four sides given to us are t-6 , t-5 , t-6 and t-5 .
Hence the perimeter of the quadrilateral would be ,
Perimeter = t-5 + t-6 + t-5 + t-6
Perimeter = 4t - 10 - 12
Perimeter = 4t - 22
Hence the perimeter of the given figure us 4t - 22.
\(\setlength{\unitlength}{1cm}\begin{picture}(0,0)\thicklines\multiput(0,0)(5,0){2}{\line(0,1){3}}\multiput(0,0)(0,3){2}{\line(1,0){5}}\put(0.03,0.02){\framebox(0.25,0.25)}\put(0.03,2.75){\framebox(0.25,0.25)}\put(4.74,2.75){\framebox(0.25,0.25)}\put(4.74,0.02){\framebox(0.25,0.25)}\multiput(2.1,-0.7)(0,4.2){2}{$\sf\large t-5$}\multiput(-1.4,1.4)(6.8,0){2}{$\sf\large t-6$}\put(-0.5,-0.4){\bf A}\put(-0.5,3.2){\bf D}\put(5.3,-0.4){\bf B}\put(5.3,3.2){\bf C}\end{picture} \)
After a picnic, (11)/(12) of the cornbread is left over. Val eats (2)/(11) of the leftover cornbread. What fraction of the combread does Val eat? Enter your answer in simplest fo. Val eats of the cornbread.
Answers
The fraction of the cornbread that Val eats from the leftover 11/12 of the cornbread after a picnic in simplest form is 1/3.
Given that:
(11)/(12) of the cornbread is left over
Val eats (2)/(11) of the leftover cornbread.
We are to find what fraction of the cornbread does Val eat.
Val eats (2)/(11) of the (11)/(12) of the cornbread = (2/11) × (11)/(12) = 2/6 = 1/3.
∴ Val eats 1/3 of the cornbread.
To know more about fraction refer here:
https://brainly.com/question/29546542
#SPJ11
Help me pleasee !!!!!

Answers

2. The parameter "b": Compare the graphs of several different exponential growth functions in
Mathematica to discover the significance of the parameter "b". Explain in detail what the
parameter "b" tells you about the graph of an exponential growth function.
Answers
Answer:
See explanation
Step-by-step explanation:
Required
The significance of "b" in exponential function
An exponential function is represented as:
\(y = ab^x\)
In the above equation, parameter "b" is the rate of the function
In other words, the constant multiplier of the function.
Take for instance;
\(y = 2*4^x\)
By comparison:
\(b = 4\)
Another instance is:
\(y = 2(-4)^x\)
By comparison
\(b = -4\)
Other significance of parameter b are:
If \(b > 0\) then b represents a growth factor
If \(b < 0\) the b represents the factor of decay
\(b \ne 0\) i.e. b is never 0
A triangle has side lengths of 13, 9, and 5. Is the triangle a right triangle? Explain.
2Points
Use complete sentences in your explanation.
Hint: Pythagorean Theorem: a^2+ b^2 = c^2
Answers
Answer: This triangle is not a right triangle
Step-by-step explanation:
In a right triangle, the hypotenuse(c) is always the longest side and a and b are the shorter sides. Thus, 5^2+9^2=13^2. Simplify this to get 25+81=169, then 106=169. Because 106 does not equal 169, it is not a right triangle.
Hope it helps <3