The seventh- and eighth-grade classes surveyed 180 of their classmates to help decide which of three options is best to raise money for school activities. Some results of the survey are given here:
66 participants preferred having a car wash.
50 participants preferred having a bake sale.
64 participants preferred having a talent show.
98 participants were seventh graders.
16 seventh-grade participants preferred having a talent show.
15 eighth-grade participants preferred having a bake sale.
a. Complete the two-way frequency table that summarizes the data on grade level and options to raise money.
Car Wash Bake Sale Talent Show Total
Seventh Graders
Eighth Graders
Total
b. Calculate the row relative frequencies. Round to the nearest thousandth.
Car Wash Bake Sale Talent Show
Seventh Graders
Eighth Graders
Question 2
c. Is there evidence of an association between grade level and preferred option to raise money?
Explain your answer
Answers
c. Yes, there is evidence of an association between grade level and preferred option to raise money.
How is the association between grade level and the preferred option to raise money determined?a. The completed two-way frequency table summarizing the data on grade level and options to raise money is as follows:
Car Wash | Bake Sale | Talent Show | Total
Seventh Graders\(| 66 | 15 | 16 | 98\)
Eighth Graders \(| - | 50 | - | 50\)
Total \(| 66 | 65 | 16 | 148\)
Note: The "-" indicates that no data is available for those specific combinations.
b. To calculate the row relative frequencies, we divide each cell value by the corresponding row total and round to the nearest thousandth:
Car Wash | Bake Sale | Talent Show
Seventh Graders \(| 0.673 | 0.153 | 0.163\)
Eighth Graders \(| - | 1.000 | -\)
Total \(| 0.446 | 0.439 | 0.115\)
c. To determine if there is evidence of an association between grade level and preferred option to raise money, we can observe the row relative frequencies. If the relative frequencies differ substantially between the rows, it suggests an association. In this case, since the row relative frequencies for each option vary between the seventh and eighth graders, there is evidence of an association between grade level and the preferred option to raise money.
Learn more about frequency
brainy.com/question/5102661
#SPJ11
Related Questions
solve the equation r −18.6 = 21.9 for x.
Answers
Answer:
r = 40.5
Step-by-step explanation:
brainliest pls :3
Answer:
X=6,3
Step-by-step explanation:
20 PTS!!!! HELP!!!!! Look at picture

Answers
Answer:
b only
Step-by-step explanation:
What is the equation of the line that passes through the point (-1,6) and has a y-intercept of -5
Answers
well, since the y-intercept is at -5, or namely when the line hits the y-axis is at -5, that's when x = 0, so the point is really (0 , -5), and we also know another point on the line, that is (-1 ,6), to get the equation of any straight line, we simply need two points off of it, so let's use those two
\(\stackrel{y-intercept}{(\stackrel{x_1}{0}~,~\stackrel{y_1}{-5})}\qquad (\stackrel{x_2}{-1}~,~\stackrel{y_2}{6}) \\\\\\ \stackrel{slope}{m}\implies \cfrac{\stackrel{rise} {\stackrel{y_2}{6}-\stackrel{y1}{(-5)}}}{\underset{run} {\underset{x_2}{-1}-\underset{x_1}{0}}} \implies \cfrac{6 +5}{-1} \implies \cfrac{ 11 }{ -1 } \implies - 11\)
\(\begin{array}{|c|ll} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{(-5)}=\stackrel{m}{- 11}(x-\stackrel{x_1}{0}) \implies y +5 = - 11 ( x -0) \\\\\\ y+5=-11x\implies {\Large \begin{array}{llll} y=-11x-5 \end{array}}\)
Which of the following shows the greatest percent increase?
A. 50 increased to 75
B. 500 increased to 700
C. 5,000 increased to 7,000
D. 50,000 increased to 74,000
Answers
50 increased to 75 (option A) shows the greatest percent increase.
How to solve for percentage increase?To determine which of the given options shows the greatest percent increase, we can calculate the percent increase for each option using the following formula:
percent increase = (new value - old value) / old value x 100%
Using this formula, we can calculate the percent increase for each option as follows:
A. percent increase = (75 - 50) / 50 x 100% = 50%
B. percent increase = (700 - 500) / 500 x 100% = 40%
C. percent increase = (7,000 - 5,000) / 5,000 x 100% = 40%
D. percent increase = (74,000 - 50,000) / 50,000 x 100% = 48%
Therefore, the option that shows the greatest percent increase is option A, which increased from 40 to 75, a percent increase of 50%.
Learn about percentage increase here https://brainly.com/question/11360390
#SPJ1
what is the perimeter of a polygon that has the coordinates of (-3,2) (2,2) (2,-4) (-1,-4) (-1,-2) (-3,-2) (-3,2)
Answers
The perimeter of a polygon is 24 units.
In this question, we have been given the coordinates of a polygon.
we need to find the perimeter of a polygon.
Let A= (-3,2), B = (2,2), C = (2,-4), D = (-1,-4), E = (-1,-2), F = (-3,-2)
First we find the length of each side of a polygon.
|AB| = √5² + 0²
|AB| = 5
|BC| = √0² + (-6)²
|BC| = 6
|CD| = √(-3)²+0²
|CD| = 3
|DE| = √0²+2²
|DE| = 2
|EF| = √(-2)²+0²
|EF| = 2
|FA| = √0²+4²
|FA| = 4
The perimeter of a polygon would be,
P = AB + BC + CD + DE + EF + FA
P = 5 + 6 + 3 + 2 + 2 + 4
P = 24 units
Therefore, the perimeter of a polygon is 24 units.
Learn more about the perimeter of a polygon here:
https://brainly.com/question/15387363
#SPJ1
Sahar walked the school track on 18 of the last 30 school days in March. Which
value is equivalent to the fraction of school days Sahar walked the track in
March?
A. 60%
B. 0.06
C. 0.183
D. 53%
Answers
explanation sana makatulong po
the average lifespan of a set of tires is 38,000 miles, with a standard deviation of 1500 miles. What is the probability that the lifespan of a set of tires will be between 32,00 miles and 44,00 miles
Answers
The probability that the lifespan of a set of tires will be between 32,000 and 44,000 miles is approximately 0.99994 or 99.994%.
To solve this problem, we'll use the concepts of normal distribution, z-scores, and the z-table.
Calculate the z-scores for the given mileage values.
To calculate the z-score, use the formula: z = (X - μ) / σ
For 32,000 miles:
z1 = (32,000 - 38,000) / 1,500 = -6,000 / 1,500 = -4
For 44,000 miles:
z2 = (44,000 - 38,000) / 1,500 = 6,000 / 1,500 = 4
Look up the z-scores in the z-table and find the corresponding probabilities.
For z1 = -4, the z-table gives a probability of approximately 0.00003 (essentially 0).
For z2 = 4, the z-table gives a probability of approximately 0.99997.
Calculate the probability of the lifespan being between 32,000 and 44,000 miles.
Subtract the probability of z1 from the probability of z2:
P(32,000 < X < 44,000) = P(z2) - P(z1) = 0.99997 - 0.00003 = 0.99994.
For similar question on probability.
https://brainly.com/question/12911628
#SPJ11
Find f (5)
quick can someone answer meee

Answers
Answer:
f (5) = 4
Step-by-step explanation:
First we need to find f(x)
To do this we can find the gradient of the line then plug it into the formula for an equation of a line.
using the points on the line, (3,0) (0,-6)
gradient, m :
\( \frac{y1 - y2}{x1 - x2} \)
\( \frac{0 - ( - 6)}{3 - 0} = \frac{6}{3} = 2\)
therefore the gradient was found to be 2.
Equation of a line:
y - y1 = m( x - x1)
y - 0 = 2( x - 3)
y = 2x - 6
Therefore the function of the line was found to be:
f(x) = 2x -6
so to find f(5) we substitute 5 in the place of x:
f(5) = 2(5) - 6
f(5) = 10 - 6
f(5) = 4
What is the polar form of -2√3 -6i? Help!
2√6 (cosine (2π/3) + i sine (2π/3) )
4√3 (cosine (2π/3) + i sine (2π/3) )
2√6 (cosine (4π/3) + i sine (4π/3) )
4√3 (cosine (4π/3) + i sine (4π/3) )
Answers
The polar form of the complex number z = - 2√3 - i 6 is z = (4√3) · (cos 4π / 3 + i sin 4π / 3). (Correct choice: D)
What is the polar form of a complex number in rectangular form?
Complex numbers are numbers of the form z = a + i b, where a and b are real numbers. This form is known as rectangular form. The polar form equivalent to that number is:
z = r · (cos θ + i sin θ)
Where:
r - Norm of the complex number.θ - Direction of the complex number, in radians.The norm and the direction of the complex number are, respectively:
r = √(a² + b²)
θ = tan⁻¹ (b / a)
If we know that a = - 2√3 and b = - 6, then the polar form of the complex number is:
r = √[(- 2√3)² + (- 6)²]
r = 4√3
θ = tan⁻¹ [(- 6) / (- 2√3)]
θ = 4π / 3
z = (4√3) · (cos 4π / 3 + i sin 4π / 3)
To learn more on polar form of complex numbers: https://brainly.com/question/24245821
#SPJ1
When water is frozen ________. Question 10 options: it shrinks by 15 percent it expands by 15 percent it shrinks by 9 percent it expands by 9 percent nothing happens to it
Answers
When water is frozen, it expands by 9 percent. This is due to the unique structure of water molecules.
In liquid form, water molecules are constantly moving and bumping into each other, but when water freezes, the molecules arrange themselves into a crystalline structure with hydrogen bonds between them. These hydrogen bonds cause the water molecules to move further apart from each other, resulting in an increase in volume and expansion.
This expansion of water when it freezes can have significant effects on the environment. For example, in colder regions, frozen water in soil can cause the soil to expand and contract, which can damage roads and buildings. In addition, the expansion of water in pipes during freezing temperatures can cause pipes to burst, leading to costly repairs.
It is important to note that not all liquids behave like water when frozen. For instance, some liquids, such as mercury, actually contract when they freeze. Therefore, it is essential to understand the properties of different substances before making assumptions about their behavior when subjected to extreme temperatures.
To know more about water, refer to the link below:
https://brainly.com/question/30415232#
#SPJ11
I am really confused on all these.. Also yes there is an extra page for it but my teacher let us not do it. So only those questions.

Answers
Answer:
See below!
Step-by-step explanation:
1) 720cm - m
cm -> m = ÷ 100720 ÷ 100 = 7.22) 983 mm - m
mm -> m = ÷ 1000983 ÷ 1000 = 0.9833) 130.5kL - L
kL -> L = × 1000130.5 × 1000 = 1305004) 0.03 g - mg
g -> mg = × 10000.03 × 1000 = 305) 997 g - kg
g -> kg = ÷ 1000997 ÷ 1000 = 0.9976) 9.1 l - ml
l -> ml = × 10009.1 × 1000 = 91007)3.75 c - ml
c ->ml = × 236.593.75 × 236.59 = 887.21258) 41.8 in - cm
in -> cm = × 2.542.54 × 41.8 = 106.1729) 156.25 lb - kg
lb -> kg = × 0.4536156.25 × 0.4536 = 70.87510) 9.5 gal - l
gal -> l = × 3.799.5 × 3.79 = 36.00511) 680.4 g - lb
g -> lb = ÷ 453.6680.4 ÷ 453.6 = 1.512) 4.725 m - ft
m -> ft = ÷ 0.34.725 ÷ 0.3 = 15.75Hope this helps, have a lovely day! :)
1.through:(5,-1), perp. to y=5/4x-2
2. through:(2,3). perp. to y=-2/5x+2


Answers
Answer:
\(y=-\frac{4}{5} x+3\)\(y=\frac{5}{2} x-2\)
How many feet per second is 1 mph?
Answers
Answer:
1.47 feet per second
Step-by-step explanation:
12345678910
How many
2
5
cup servings are in
9
5
cups of ice cream? (in simplest fraction form)
Answers
There would be 5/2 cup servings
What is the solution for this system of equations

Answers
Explanation-the two line intersects at point -1,7
a car travels at an average speed of 68 miles per hour. how long does it take to travel 612 miles
Answers
It takes 9 hours for the car to travel 612 miles at an average speed of 68 miles per hour.
To find the time it takes for the car to travel 612 miles at an average speed of 68 miles per hour, we can use the formula:
time = distance ÷ speed
Plugging in the given values, we get:
time = 612 miles ÷ 68 miles per hour
Therefore, the time it would take the car to travel 612 miles is: Time = 612 miles / 68 miles per hour Time = 9 hours. So, it would take the car approximately 9 hours to travel a distance of 612 miles if it maintains an average speed of 68 miles per hour.
Know more about time here:
https://brainly.com/question/28050940
#SPJ11
3. Which of the following has a value that is
less than zero?
a. (-6)2
b. (32
c. 0.52
d. -72
Answers
Answer:
d) -72
Step-by-step explanation:
The value of negative integers is always less than zero.
So, (-72) is the answer
(-6)² = (-6) * (-6) = 36. Which is greater than 0
Orthogonal complement to S has dimension 0 when ____.
Answers
The orthogonal complement to S has dimension 0 when the dimension of the vector space is equal to the dimension of S.
We have,
The orthogonal complement to a subspace S of a vector space is the set of all vectors in the vector space that are orthogonal (perpendicular) to every vector in S.
The dimension of the orthogonal complement is given by the difference between the dimension of the vector space and The dimension of S.
If S spans the entire vector space, then its orthogonal complement consists only of the zero vector and therefore has dimension 0.
Thus,
The orthogonal complement to S has dimension 0 when the dimension of the vector space is equal to the dimension of S.
Learn more about subspace here:
https://brainly.com/question/30318872
#SPJ4
Please i need your help! What is the slope of each line segment of QRS
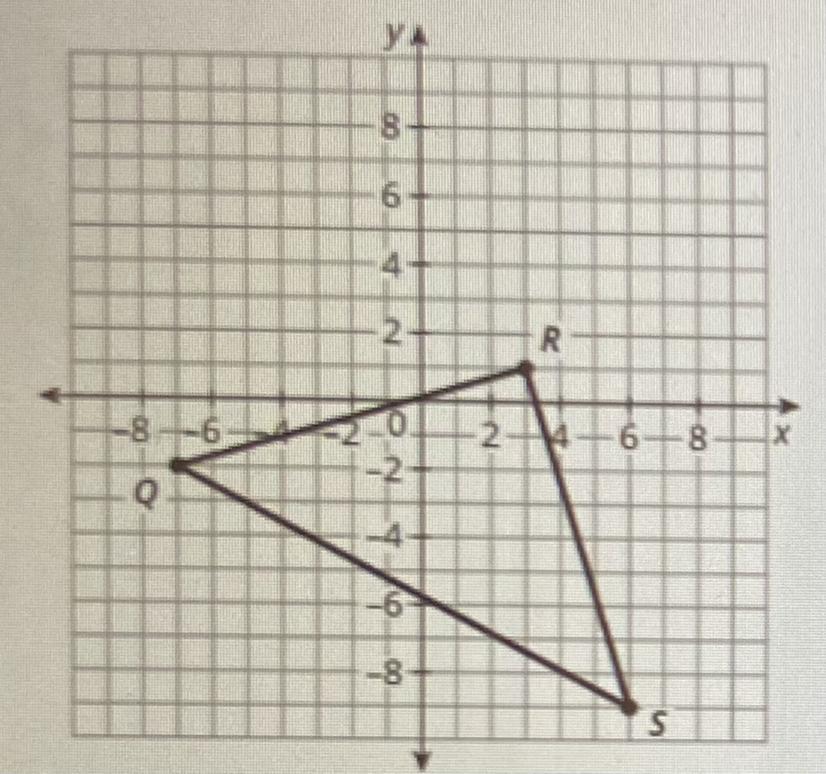
Answers
Answer:ez 90 degrees
Step-by-step explanation:
Find the slope of the following (-5, -5), (-14, -9)
(19,-6), (12, 20)
(-14, 17), (14, 17)
Answers
Answer:
1. m=4/9
2.m=-26/7
3.m=0
Step-by-step explanation:
Formula: Y=mx+b
1.y = 4 /9 x − 25 /9
2.y = − 26 /7 x + 452 /7
3.y=17
✨Hope this helps!✨
can anyone help pls?

Answers
\(7 \frac{5}{8} + 4 \frac{2}{3} \)
to find:the simplest form.
solution:\( \frac{61}{8} + \frac{14}{3} \)
\( = \frac{(61 \times 3) + (14 \times 8)}{8 \times 3} \)
\( = \frac{183 + 112}{24} \)
\( = \frac{295}{24} \)
\( = 12 \frac{7}{24} \)
hence, the correct answer is option D.
the scores of individual students on the american college testing (act) program composite college entrance examination have a normal distribution with mean 18.6 and standard deviation 6.0. forty-nine randomly selected seniors take the act test. what is the probability that their mean score is greater than 20? round your answer to 4 decimal places.
Answers
The probability that the mean score of the 49 seniors is greater than 20 is 0.0516. To solve this problem, we need to use the central limit theorem, which states that the distribution of sample means from a population with any distribution will approach a normal distribution as the sample size increases.
First, we need to find the standard error of the mean (SEM), which is the standard deviation of the sampling distribution of the mean. We can use the formula SEM = σ / √n, where σ is the population standard deviation, and n is the sample size.
In this case, σ = 6.0 and n = 49, so SEM = 6.0 / √49 = 0.857.
Next, we need to standardize the sample mean using the z-score formula: z = (x - μ) / SEM, where x is the sample mean, μ is the population mean, and SEM is the standard error of the mean.
In this case, x = 20, μ = 18.6, and SEM = 0.857, so z = (20 - 18.6) / 0.857 = 1.63.
Finally, we need to find the probability that a standard normal distribution is greater than 1.63, which is 0.0516 when rounded to 4 decimal places.
Therefore, the probability that the mean score of the 49 seniors is greater than 20 is 0.0516.
Learn more about probability here:
brainly.com/question/27342429
#SPJ11
The value of Desmond's home is modeled by the function V (x) = 275,000(1.09) ²/³x, where x is the number of years since 2012. By what approximate percentage rate is the value of Desmond's home increasing per year?
Answers
Answer:
6%Step-by-step explanation:
Given function
V(x) = 275000(1.09)^(2/3x)Every year the value is changing at the rate:
(1.09)^(2/3) = 1.059 ≈ 1.06The rate of 1.06 is equivalent of 6% increase per year
does anyone know what 3 x (8+2) x 5 is? i really need it for homework due tomorrow thank you!
Answers
3 x 10 x 5
30 x 5
= 150
Simplify: 3.2/0.4 •2• 0.4/0.1
option 1) 64
option 2) 16
option 3) 6.4
option 4) 1.6
Answers
Answer:
1
Step-by-step explanation:
3.2/0.4=8
8×2=16
16×0.4=6.4
6.4÷0.1=64
fail 59 45 67 after running an independence test, can it be concluded that pass/fail rates are dependent on school?
Answers
The correct option is B
No, it cannot be concluded that pass/fail rates are dependent on school because the p-value = 0.9373.
What is meant by an alternative hypothesis?In statistical hypothesis testing, the alternative hypothesis is one of the suggested propositions in the hypothesis test. In general, the purpose of a hypothesis test is to demonstrate that, under the given conditions, there is sufficient evidence to support the believability of an alternate hypothesis rather than the test's exclusive statement (null hypothesis). Because it is based on a review of the literature and previous studies, it is usually congruent with the research hypothesis.
Null hypothesis : H₀ : pass/fail rates are independent on school
Alternative Hypothesis : H₁: pass/fail rates are dependent on school
Test Statistic is,
x²stat=∑(O-E)²/E
Here O is the observed frequency and E is the Expected frequency.
E=(Row total× Column total)/Grand total
O E O-E (O-E)² (O-E)² /E
40 41.4184 -1.4184 2.-118 0.0486
33 32.6327 0.3673 0.1349 0.0041
50 48.9490 1.0510 1.1046 0.0226
59 57.5816 1.4184 2.0118 0.0349
45 45.3673 -0.3673 0.1349 0.0030
67 68.0510 -1.0510 1.1046 0.0162
Total=0.1294
Degrees of freedom=(Number of rows-1)×(Number of columns-1)
=(2-1)×(3-1)
=2
p-value=P(x²>x²stat)=P(x²>0.1294)
For 3 degrees of freedom,
P(x²>0.1294)=0.9373
Level of significance α=0.10
As p-value is 0.9373>α:0.10
Fail to reject the null hypothesis.
To know more about alternative hypothesis, visit:
https://brainly.com/question/27335001
#SPJ4
MATLAB!
Hello, There is this question which i struggle to understand. Can you please explain it to me, every line step by step and how it contributes to the answer. (The subplot part I got it) Thank you.
State whether or not the system is linear, time invarient, causal, stable, and invertible.
Answer:b) y[n] = nx[n] Answer: n= [-3: 3]; x= [0 0 0 2 4 2 1]; y=n. *x; n1=n+2; x2=n. *x; y_n2= (n-2). *x; figure (1) subplot (3, 1, 1), stem (n,x, 'filled') title ('x[n]') axis ([-4 6 0 5]) subplot (3,1,2), stem (n, y, 'filled') title ('y[n]') axis ([-4 6 0 5]) subplot (3,1,3), stem (n, (y./n), 'filled '5 title ('y [n]/n') axis ([-4 6 0 5]) figure (2) subplot (3,1,1), stem (n, y, 'filled') title ('y [n] ¹) 5 axis ([-4 6 0 5])
subplot (3,1, 2), stem (n1, x2, 'filled') title ('n*x [n-2]'). axis ([-4 6 0 5]) 0 subplot (3, 1, 3), stem (nl, y_n2, 'filled') title('y [n-2] =(n-2) x [n-2] ¹) 5 axis ([-4 6 0 5])
Answers
The given signal is, y[n] = nx[n] .It needs to be analyzed if the given system is linear, time invarient, causal, stable, and invertible.
Linear: We know a system is linear if it follows the superposition principle. That is, if x1[n] → y1[n] and x2[n] → y2[n] are two input-output pairs, then for any constants a1 and a2, we must have a1x1[n] + a2x2[n] → a1y1[n] + a2y2[n]. Hence, in this case, we must check if the superposition principle holds true. The given system is linear because n is simply a constant, and the multiplication of any constant with a signal does not change its linearity property. Therefore, y1[n] = n x1[n] and y2[n] = n x2[n] and a1y1[n] + a2y2[n] = a1 (n x1[n]) + a2 (n x2[n]) = n (a1x1[n] + a2x2[n]) satisfies the superposition principle.
- Time invarient: A system is time-invariant if its output does not depend on the absolute value of time. Thus, a time-invariant system does not change its properties over time. Hence, in this case, we must check if the system is time-invariant. The given system is time-invariant as it does not explicitly depend on time. The function of n is merely to scale the input by a constant value. As scaling the input does not change its position on the time-axis, the system is time-invariant.
- Causal: A system is causal if its output only depends on the present and past values of the input. The output must not be affected by future values of the input. Hence, in this case, we must check if the system is causal. The given system is not causal because the value of y[n] depends on the future value of the input. The value of y[n] is n times the value of x[n]. Therefore, if the value of x[n] at a future time is changed, the value of y[n] will also change, which violates the causality property.
- Stable: A system is stable if its output does not diverge for any bounded input. A bounded input is an input signal that does not go to infinity. Hence, in this case, we must check if the system is stable. The given system is unstable as it multiplies the input signal with n, which increases unboundedly.
- Invertible: A system is invertible if distinct inputs have distinct outputs. In other words, if x1[n] and x2[n] are two inputs such that x1[n] ≠ x2[n], then y1[n] ≠ y2[n]. Hence, in this case, we must check if the system is invertible. The given system is not invertible because different inputs may yield the same output.
he given system is linear and time-invariant. It is not causal, unstable, and invertible.
To know more about signal visit
https://brainly.com/question/31473452
#SPJ11
3(2x + 2) - 3x = 6 + 3x
Answers
Answer:
no solution
Step-by-step explanation:
3(2x + 2) - 3x = 6 + 3x
6x + 6 - 3x = 6 + 3x
6x - 3x = 3x
3x + 6 = 6 + 3x
the answer would be
no solution
find the value(s) of c guaranteed by the Mean Value Theorem for Integrals for the function over the given interval.

Answers
Remember that
If f is continuous over [a,b] and differentiable over (a,b), then there exists c∈(a,b) such that
\(f^{\prime}(c)=\frac{f(b)-f(a)}{b-a}\)In this problem, we have the function
\(f(x)=\frac{9}{x^3}\)over the interval [1,3]
so
f(a)=f(1)=9/(1)^3=9
f(b)=f(3)=9/(3)^3=1/3
substitute
\(f^{\prime}(c)=\frac{\frac{1}{3}-9}{3-1}=\frac{-\frac{26}{3}}{2}=-\frac{26}{6}=-\frac{13}{3}\)Find out the first derivative f'(x)
\(f^{\prime}(x)=-\frac{27}{x^4}\)Equate the first derivative to -13/3
\(\begin{gathered} -\frac{27}{x^4}=-\frac{13}{3} \\ \\ x^4=\frac{27*3}{13} \\ \\ x=1.58 \end{gathered}\)therefore
The value of c is 1.58 (rounded to two decimal places)It costs james $4 to make an order of a dozen cookies. if he sells them for $16, what percentage is each order of cookies marked up? 400% 300% 75% 25%
Answers
The markup value over the each order of cookies is 300%. Thus option B is correct.
According to the statement
we have given that the James costs $4 to make an order of dozen cookies and selling prices is $16 and we have to calculate the markup on the order of cookies.
So, For this purpose, we know that the
Markup formula calculates the amount or percentage of profits derived by the company over the product's cost price.
The formula to calculate markup is :
Markup = (selling cost - production cost / production cost) *100
So, Substitute the formula in it then
Markup = (selling cost - production cost / production cost) *100
Here selling cost = $16 and production cost is $4
So,
Markup = (selling cost - production cost / production cost) *100
Markup = (16 - 4 / 4) *100
Markup = 3 *100
Markup = 300%.
So, The markup value over the each order of cookies is 300%. Thus option B is correct.
Learn more about markup value here
https://brainly.com/question/1153322
#SPJ4
Answer:
it is 400%
Step-by-step explanation:
$4* 400%= 16