Answers
Answer:
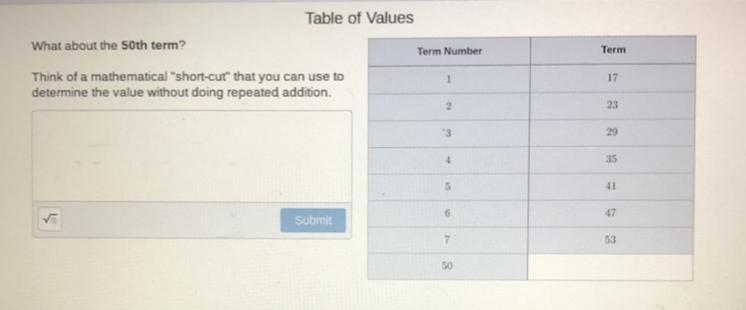
50th term would be 317
Step-by-step explanation:
The "shortcut" would be 17+6x since you have a starting value of 17 and you add 6 to each term.
Related Questions
A, B, and Care the centers of the 3 circles. Select all thesegments that are congruent to AB.

Answers
The congruent segments are the sides of the small triangles, then the congruent segments are: HA, BD and BF.
Therefore the answer are B, E and F.
Two ways to write k/3+16
Answers
The two ways to write the expression k/3+16 are 1/3k + 16 and (k + 48)/3
How to rewrite the expression?From the question, the expression is given as
k/3+16
Start by factoring 1/3 out of the first term
So, we have the following expression
1/3k + 16
The above is one of the ways of rewriting the expression
Another way is by taking the LCM
So,we have
k/3+16 = (k + 48)/3
Hence, the equivalent expressions are 1/3k + 16 and (k + 48)/3
Read more about equivalent expressions at
https://brainly.com/question/2972832
#SPJ1
What is the circumference of this circle?
A.
81π
B.
(8
1π
⁄
4
)
C.
None of the above
D.
18π
E.
(4
1π
⁄
2
)
Answers
Answer:
A.
81π
Step-by-step explanation:
PLEASE MAKE IT BRAINLIEST
PLEASE FOLLOW....
Three golf balls are stored in a square prism container with a height of 6 inches and a base edge of 2
inches. The diameter of a golf ball is 1.68 inches.
Find the amount of space within the square prism not taken up by the golf balls.
6 in
2 in
2 in
O 21.5 in
O 7.4 in
O 16.6 in
O 31.4 in
Answers
Answer:
16.6 in
Step-by-step explanation:
Amount of space left = volume of prism - volume of 3 golf balls
volume of prism = base area x height
base area = area of a square = length² = 2² = 4
volume = 4 x 6 = 24
Volume of a sphere = 4/3 x pi x r^3
r = 1.68/2 = 0.84
4/3 x 3.14 x 0.84^3 = 2.48
volume of 3 balls = 2.48 x 3 =
Please helpppppp meee

Answers
I believe the answer would be M= 132 because 48+132=180 and 180 is the degree of a straight line. I hope this makes sense! :)
Mallory records the number of hours she spends babysitting and the amounts of money she is paid. What is the constant rate of proportionality between the number of hours Mallory babysits and the amount of money she is paid, in dollars?
Please explain as well, I do not understand how I would find the answer.

Answers
Answer:
Mallory gets paid $20 for every 1 hour.
Step-by-step explanation:
You take the lowest set of numbers in this table, & divide them to find how much it would be for 1 hour: $40÷2hours= $20
ratio 1 hr./20 dollars
23. One way to approximate the value of a definite integral
1- [*f(x) dx =
is to split the interval [a, b] into n equal subintervals, each of length h, defined by the n+1 points x, = a + ih for i=0,1,2,...,n, computing the corresponding function values f(x), and taking a linear combination of these function values.
The composite trapezoidal rule is
I= f(xo) +2+) H
which has an error that is a multiple of h². The composite Simpson rule is
M m-1 1-4 (+4 () +20) +00)) f(x, F
where m n/2 and is assumed to be even. This has an error that is a multiple of h¹.
Write a program that implements these two techniques. The inputs should be a, b,n and the name of a program that evaluates the relevant function f(x). The latter program should input a vector of values x and output a vector of corresponding values y=f(x). Your program should not include any 'for loops.
Use your program to approximate the following integrals and to investigate the above claims concerning the behavior of the errors. Which technique is more accurate for a given cost ?
(1) In(x) dx = 2 In (2) – 1
(i) (1+e* sin(4x)) dx - 2)
Answers
The correct answer to the equation result = (h/3) * (y(1) + 4*sum(y(2:2:n)) + 2*sum(y(3:2:n-1)) + y(n+1));
Here's an example MATLAB code that implements the composite trapezoidal rule and the composite Simpson's rule for approximating definite integrals:
% Function to evaluate the relevant function f(x)
function y = evaluateFunction(x)
% Define the function f(x) here
y = log(x); % Example: ln(x)
end
% Composite trapezoidal rule
function result = compositeTrapezoidalRule(a, b, n)
h = (b - a) / n;
x = linspace(a, b, n+1);
y = evaluateFunction(x);
result = (h/2) * (y(1) + 2*sum(y(2:n)) + y(n+1));
end
% Composite Simpson's rule
function result = compositeSimpsonsRule(a, b, n)
h = (b - a) / n;
x = linspace(a, b, n+1);
y = evaluateFunction(x);
result = (h/3) * (y(1) + 4*sum(y(2:2:n)) + 2*sum(y(3:2:n-1)) + y(n+1));
end
% Main program
a = 1; % Lower limit of integration
b = 2; % Upper limit of integration
n = 100; % Number of subintervals
% Approximate the integral using the composite trapezoidal rule
approximation_trapezoidal = compositeTrapezoidalRule(a, b, n);
% Approximate the integral using the composite Simpson's rule
approximation_simpsons = compositeSimpsonsRule(a, b, n);
% Display the results
disp("Approximation using the composite trapezoidal rule:");
disp(approximation_trapezoidal);
disp("Approximation using the composite Simpson's rule:");
disp(approximation_simpsons);
To use this code, you need to define the function you want to integrate within the evaluateFunction function. In this example, the function evaluateFunction is defined to compute the natural logarithm of x.
You can change the values of a, b, and n to approximate different integrals. The n value determines the number of subintervals and can be adjusted to control the accuracy of the approximation.
To investigate the behavior of the errors, you can compare the approximations with the exact values of the integrals if known. You can also experiment with different values of n to observe how the errors decrease as the number of subintervals increases.
The choice of which technique is more accurate for a given cost depends on the specific function being integrated and the desired level of accuracy. Generally, the composite Simpson's rule provides a more accurate approximation than the composite trapezoidal rule for the same number of function evaluations, but it may require more computational resources.
Learn more about statistics here:
https://brainly.com/question/31527835
#SPJ11
- Find the coordinates of A if B(0,5.5) is the midpoint of AC and C has coordinates
(-3,6).
Answers
Given:
Coordinates of point C are (-3,6).
Point B(0,5.5) is the midpoint of AC.
To find:
The coordinates of A.
Solution:
Let the coordinates of point A are (a,b).
Formula for midpoint:
\(Midpoint=\left(\dfrac{x_1+x_2}{2},\dfrac{y_1+y_2}{2}\right)\)
Using the above formula, the midpoint of A(a,b) and C(-3,6) is
\(B=\left(\dfrac{a+(-3)}{2},\dfrac{b+6}{2}\right)\)
\((0,5.5)=\left(\dfrac{a-3}{2},\dfrac{b+6}{2}\right)\)
On comparing both sides, we get
\(\dfrac{a-3}{2}=0\)
\(a-3=0\)
\(a=3\)
and,
\(\dfrac{b+6}{2}=5.5\)
\(b+6=11\)
\(b=11-6\)
\(b=5\)
Therefore, the coordinates of point A are (3,5).
danny henry made a waffle on his six-inch-diameter circular griddle using batter containing a half a cup of flour. using the same batter, and knowing that all waffles have the same thickness, how many cups of flour would paul bunyan need for his -foot-diameter circular griddle?
Answers
Danny used half a cup of flour, so Paul Bunyan would need 2 cups of flour for his foot-diameter griddle.
To determine the number of cups of flour Paul Bunyan would need for his circular griddle, we need to compare the surface areas of the two griddles.
We know that Danny Henry's griddle has a diameter of six inches, which means its radius is three inches (since the radius is half the diameter). Thus, the surface area of Danny's griddle can be calculated using the formula for the area of a circle: A = πr², where A represents the area and r represents the radius. In this case, A = π(3²) = 9π square inches.
Now, let's calculate the radius of Paul Bunyan's griddle. We're given that it has a diameter in feet, so if we convert the diameter to inches (since we're using inches as the unit for the smaller griddle), we can determine the radius. Since there are 12 inches in a foot, a foot-diameter griddle would have a radius of six inches.
Using the same formula, the surface area of Paul Bunyan's griddle is A = π(6²) = 36π square inches.
To find the ratio between the surface areas of the two griddles, we divide the surface area of Paul Bunyan's griddle by the surface area of Danny Henry's griddle: (36π square inches) / (9π square inches) = 4.
Since the amount of flour required is directly proportional to the surface area of the griddle, Paul Bunyan would need four times the amount of flour Danny Henry used.
For more such questions on diameter
https://brainly.com/question/23220731
#SPJ8
What is the absolute value of -11

Answers
Answer:
11
Step-by-step explanation:
11
since it asks the absolute value of -11 it
will be 11 because in absolute value-for negatives it always positive.
Answer:
see attached
Step-by-step explanation:

HELP ME also I don't know if the ones I put are right...

Answers
The angle measure of NQL is given as follows:
m < NQL = 80º.
By the Parallelogram Consecutive Angles Theorem, <NQL and <QLM are supplementary.
What is the Parallelogram Consecutive Angles Theorem?The Parallelogram Consecutive Angles Theorem states that two consecutive interior angles in a parallelogram are supplementary, that is, the sum of their measures is of 180º.
The consecutive angles for this problem are given as follows:
< NQL.< QLM.As the measure of < QLM is of 100º, the measure of angle NQL is given as follows:
m < NQL = 180º - 100º
m < NQL = 80º.
More can be learned about the Parallelogram Consecutive Angles Theorem at https://brainly.com/question/10699442
#SPJ1
Fill in the blank: Some of the most common symbols used in formulas include (addition), - (subtraction), * (multiplication), and / (division). These are called _____.
Answers
Some of the most common symbols used in formulas include (addition), - (subtraction), * (multiplication), and / (division). These are called "operators". The correct option is c) operators.
Operators are symbols that represent a specific operation to be performed on one or more values or variables. In mathematics and programming, operators are used to build expressions that represent calculations. The most common operators include addition (+), subtraction (-), multiplication (*), and division (/), which are used to perform basic arithmetic operations.
Other operators include exponents (^), modulus (%), and comparison operators (>, <, =, etc.), which are used for more complex operations. Understanding operators is an essential part of learning mathematics and programming, as they form the building blocks for more complex calculations and algorithms. The correct option is c) operators.
The complete question is:
Fill in the blank: Some of the most common symbols used in formulas include + (addition), - (subtraction), * (multiplication), and / (division). These are called _____.
a) references
b) domains
c) operators
d) counts
For more about operators:
https://brainly.com/question/30340325
#SPJ4
Triangle BCD, with vertices B(4,-7), C(6,-8), and D(7,-2), is drawn on the coordinate
grid below.
S
Answer: A =
6
7
D
9
What is the area, in square units, of triangle BCD?
units
Submit Answer
K

Answers
Answer: The area is 6.5
How many quarts are there in 10 1⁄2 gallons?
Write an equation to show your work
plz answer fast it is a test!
Answers
Answer:
42 quarts
Step-by-step explanation:
There are 4 quarts in one gallon, so you'd just multiply.
Help please I need this asap

Answers
Answer:
It is a little hard to see. I think that it is 10.
Step-by-step explanation:
They break even where the two lines intersect. If you look at the bottom of the graph and find 10 and then trace that straight up, I think that is where I see the lines crossing.
1. Doug digs a hole that is 1.7 feet below ground
level. He plants a bush that is 3 2/10 feet tall from
the bottom of the root to the top branch. How
much of the bush is above the ground?
Answers
Answer:
1.5 feet of the Bush is still above ground
Step-by-step explanation:
3 2/10= 3.2
3.2-1.7=1.5
If dtdr(t)=⟨−tet,4e2t,8tet2> and r(0)=⟨1,1,2>. Then ∣r(1)∣ is equal to: 15.13806773431206 14.636867734312059 17.922567734312061 17.709167734312061 16.38806773431206
Answers
The correct answer is: ∣r(1)∣ is equal to 17.709167734312061, that is the magnitude of vector .
To find the magnitude of vector r(1), we need to integrate the vector function dt/dr(t) from t = 0 to t = 1 and then evaluate it at t = 1.
Given dtdr(t) = ⟨-te^t, 4e^(2t), 8te^(t^2)⟩ and r(0) = ⟨1, 1, 2⟩, we can integrate each component of dtdr(t) separately with respect to t.
Integrating the first component: ∫(-te^t) dt = -te^t + e^t + C1
Integrating the second component: ∫(4e^(2t)) dt = 2e^(2t) + C2
Integrating the third component: ∫(8te^(t^2)) dt is not a straightforward integral and might not have an elementary solution.
To find the constants C1 and C2, we can substitute t = 0 and equate it to r(0). From r(0) = ⟨1, 1, 2⟩, we get the following equations:
-0e^0 + e^0 + C1 = 1 => C1 + 1 = 1 => C1 = 0
2e^(2*0) + C2 = 1 => 2 + C2 = 1 => C2 = -1
With C1 = 0 and C2 = -1, we can determine the vector function r(t) by integrating each component:
r(t) = ⟨\(\int(-te^t) dt + 1, \int (4e^(2t)) dt - 1, \int (8te^(t^2)) dt + 2\)⟩
r(t) = ⟨\(-te^t + e^t + 1, 2e^(2t) - 1, \int (8te^(t^2)) dt + 2\)⟩
To find the magnitude of r(1), we substitute t = 1 into the vector function r(t) and evaluate it:
r(1) = ⟨\(-(1)e^1 + e^1 + 1, 2e^(2*1) - 1, \int(8te^(1^2)) dt + 2\)⟩
r(1) = ⟨-e + e + 1, 2e^2 - 1, ∫(8te) dt + 2⟩
r(1) = ⟨1, 2e^2 - 1, 8∫(te) dt + 2⟩
The first and second components are straightforward, but the third component involves integrating te with respect to t. We can evaluate this integral:
∫(te) dt = t^2e/2 - ∫(t^2e/2) dt
∫(te) dt = t^2e/2 - ∫(t^2/2)e dt
∫(te) dt = t^2e/2 - (1/2)∫(t^2)e dt
∫(te) dt = t^2e/2 - (1/2)(t^3/3)
∫(te) dt = t^2e/2 - t^3/6 + C3
Substituting t = 1 into this expression, we get:
∫(te) dt = (1^2e)/2 - (1^3)/6 + C3
∫(te) dt = e/2 -
Learn more about vector here:
https://brainly.com/question/15650260
#SPJ11
Similar Polygons
DEFG is similar to HJKL. What is the length of LK?
A) 5
B)21
C) 80/3
D) 60

Answers
Answer:
I think it's 21. .........
beth invests £5600 at a sample interest rate of 11% per year
work out the value of the investment after 3 years
Answers
Answer:
5600 ×11/100 = 616
616 × 3 = 1848
£5600 + £1848 = £7448
Step-by-step explanation:
Using the sample interest rate, we know that the value of investment after 3 years will be £7,448.
What is the interest rate?With the help of the interest rate formula, we can calculate the interest rate, which is the percentage of the principal sum that the lender or bank would charge the borrower in exchange for using its assets or money for a given period of time. Interest Rate = (Simple Interest × 100)/(Principal × Time) is the formula for calculating interest rates.So, the value of the investment after 3 years will be:
The invested amount is £5600.The interest rate is 11% per year.Then, calculate as follows:
5600/100 × 11616 × 3 (3 years)1,848 = 3 years of interestTotal investment value: 5600 + 1848 = £7,448
Therefore, using the sample interest rate, we know that the value of investment after 3 years will be £7,448.
Know more about the interest rates here:
https://brainly.com/question/25793394
#SPJ2
You are designing a 5 kilometer course for a local charity run. your assistants provide you with the following measures in yards. you need to convert the distances to kilometers, and then tell your assistants how much further they need to extend the finish line to complete the course.
course streets distance
main street to 6th ave. 781 yards
6th ave. to pleasant road 1,250 yards
pleasant road to city park 275 yards
route through city park 2,337 yards
city park to main street 725 yards
Answers
You are designing a 5 kilometer course for charity run. The design now has been covers 4,908.5 meters, hence, you need to add more 91.5 meters on the course.
The conversion from yard to meter is:
1 yard = 0.9144 meters
The course streets and the distances after converted into meters are:
main street to 6th ave. 781 yards = 714.15 meters
6th ave. to pleasant road 1,250 yards = 1143 meters.
pleasant road to city park 275 yards = 251.46 meters
route through city park 2,337 yards = 2,136.95 meters
city park to main street 725 yards = 662.94 meters
Total course = 714.15 + 1143 + 251.46 + 2,136.95 + 662.94
Total course = 4,908.5 meters
The design is 5 km = 5000 meters. Therefore, you still need to add:
5000 - 4,908.5 = 91.5 meters more course.
Learn more about measurement unit here:
https://brainly.com/question/7716790
#SPJ4
A rectangular wading pool measures 7 feet by 6 feet by 2.5 feet. When the pool is empty, it weighs 35 pounds. If water weighs 6.24 pounds per cubic foot, what is the total weight of the pool when it is full of water?
Answers
Answer:
The total weight of the pool when it is full of water is 690.2 pounds.
Step-by-step explanation:
We know that total weight of the wading pool (\(m_{T}\)) is the sum of the weight of empty pool (\(m_{pool}\)) and the weight of water (\(m_{w}\)), all measured in pounds, that is:
\(m_{T} = m_{pool} + m_{w}\)
The weight of water can be determined by definition of density, as we know the geometry of the wading pool and density of water:
\(m_{w}=\rho_{w}\cdot (w\cdot h\cdot l)\)
Where:
\(\rho_{w}\) - Density, measured in pounds per cubic foot.
\(w\), \(h\), \(l\) - Width, height and length of the wading pool, measured in feet.
Now, we are noticed that \(\rho_{w} = 6.24\,\frac{pd}{ft^{3}}\), \(w = 7\,ft\), \(h = 6\,ft\), \(l = 2.5\,ft\) and \(m_{pool} = 35\,pd\) and the total weight of the pool when it is full of water is:
\(m_{w} = \left(6.24\,\frac{pd}{ft^{3}} \right)\cdot (7\,ft)\cdot (6\,ft)\cdot (2.5\,ft)\)
\(m_{w} = 655.2\,pd\)
\(m_{T} = 35\,pd + 655.2\,pd\)
\(m_{T} = 690.2\,pd\)
The total weight of the pool when it is full of water is 690.2 pounds.
find equations of the line that is parallel to the z-axis and passes through the midpoint between the two points (0, −2, 7) and (−2, 3, 5). (enter your answers as a comma-separated list of equations.)
Answers
The equations of the line parallel to the z-axis and passing through the midpoint between the two given points are x = -1, y = 0.5, and z = t, where t represents the distance along the z-axis.
Since the line is parallel to the z-axis, its direction vector will be (0, 0, 1). Now, let's find the midpoint between the two given points:
Midpoint = ((0 + (-2))/2, (-2 + 3)/2, (7 + 5)/2)
= (-1, 0.5, 6)
Therefore, the line parallel to the z-axis and passing through the midpoint (-1, 0.5, 6) can be represented by the following set of parametric equations:
x = -1 (remains constant)
y = 0.5 (remains constant)
z = t (where t is a parameter representing the distance along the z-axis)
In Cartesian form, the equation of the line can be written as:
x = -1
y = 0.5
z = t
To learn more about midpoint
https://brainly.com/question/896396
#SPJ11
8 feet wide and 11 feet long. Tori wants to stain the wood on the porch next weekend. The stain costs $1. 00 per square foot. How much will it cost to buy enough stain for the whole porch?
Answers
Tori will need to spend $88.00 to buy enough stain for the whole porch. The total area of the porch can be calculated as follows:
Area = length x width
Area = 8 feet x 11 feet
Area = 88 square feet
Since the cost of the stain is $1.00 per square foot, we can calculate the total cost of the stain needed for the porch by multiplying the area of the porch by the cost per square foot of the stain:
Total cost of stain = Area x Cost per square foot
Total cost of stain = 88 square feet x $1.00/square foot
Total cost of stain = $88.00
Therefore, Tori will need to spend $88.00 to buy enough stain for the whole porch.
learn more about total area here
https://brainly.com/question/29261605
#SPJ11
what is -15 = -5b ?
Answers
To solve this equation you: divide both sides of the equation into -5:
\(\begin{gathered} \frac{-15}{-5}=\frac{-5}{-5}b \\ 3=b \end{gathered}\)Then, the solution for the given equation is b=3How many nets are there for a triangular pyramid?
Answers
The net of a triangular pyramid consist of a total of 4 triangles. it has 4 faces with the base being one of them which is also in the shape of a triangle.
A net of the triangular pyramid is the pattern formed when the surface of it is laid out flat showing each triangular face of the figure, therefore we know that the net of a triangular pyramid consist of a total of 4 triangles.
Triangular pyramid is a pyramid which has a triangular base. In geometry, vertices are essentially corners. All triangular-based pyramids, either regular or irregular, have four vertices.
It has 6 edges, 4 faces, 4 vertices.
A regular triangular pyramid has equilateral triangles all four faces
To learn more about triangular pyramids, click here:
brainly.com/question/22213308
#SPJ4
How do I find the value of two numbers if their sum is 12 and their difference is 4?
Answers
Answer:
The value of two numbers if their sum is 12 and their difference is 4 are 8 and 4.
Step-by-step explanation:
I hope this helped
A diver dove from a board that was 10.75 feet above the water's surface, and descended until he was 8.5 feet below the water's surface. What was the total distance that the diver descended?
Answers
Answer: 2.25
Step-by-step explanation: 2.25 because if u subtract 10.75 - 8.5 = 2.25
\begin{tabular}{|rrl} \multicolumn{2}{|c}{ Taxable Income } & Tax Rate \\ \hline$0− & 9,950 & 10% \\ 9,950− & 40,525 & 12 \\ 40,525− & 86,375 & 22 \\ 86,375−164,925 & 24 \\ 164,925−209,425 & 32 \\ 209.425−523,600 & 35 \\ 525.600+ & & 37 \\ \hline \end{tabular} 5. Calculating Taxes Duela Dent is single and had $189,000 in taxable income. Using the rates from Table 2.3 in the chapter, calculate her income taxes. What is the average tax rate? What is the marginal tax rate?
Answers
Duela Dent's income taxes can be calculated using the given tax rates and her taxable income of $189,000. Her average tax rate and marginal tax rate can also be determined.
To calculate Duela Dent's income taxes, we need to determine the tax amount for each tax bracket that her taxable income falls into.
The taxable income of $189,000 falls into the following tax brackets:
$0-$9,950: Not applicable
$9,950-$40,525: ($40,525 - $9,950) * 12% = $3,546
$40,525-$86,375: ($86,375 - $40,525) * 22% = $9,992
$86,375-$164,925: ($164,925 - $86,375) * 24% = $19,110
$164,925-$209,425: ($189,000 - $164,925) * 32% = $7,744
$209,425-$523,600: Not applicable
$525,600 and above: Not applicable
Summing up the tax amounts for each bracket, Duela Dent's income taxes amount to $40,392.
The average tax rate is calculated by dividing the total tax amount ($40,392) by the taxable income ($189,000) and multiplying by 100:
Average Tax Rate = ($40,392 / $189,000) * 100 ≈ 21.37%
The marginal tax rate refers to the tax rate applied to an additional dollar of income. In this case, Duela Dent's marginal tax rate is 32%, which corresponds to the tax rate of the last bracket her taxable income falls into.
Learn more about income taxes here:
https://brainly.com/question/21595302
#SPJ11
You are the marketing manager for Coffee Junction. The revenue for the company is given by R(x)=− 32x 3+6x 2+18x+4 where R(x) is revenue in thousands of dollars and x is the amount spent each month on advertisement, in thousands of dollars. 0≤x≤25 a) At what level of advertising spending does diminishing returns start? Explain What this diminishing returns means for this company. b) How much revenue will the company earn at that level of advertising spending? c) What does 0≤x≤25 tell us with respect to this problem?
Answers
a) Diminishing returns start at x = 1, where the marginal revenue will be less than the marginal cost
b)At x = 1, the company will earn R(1) = -32 + 6 + 18 + 4 = -4,000 dollars.
c) 0 ≤ x ≤ 25 implies that the Coffee Junction company has the capacity to spend a maximum of 25,000 dollars per month on advertisements.
a) At what level of advertising spending does diminishing returns start?
Diminishing returns refers to a situation when the marginal return on investment decreases as more resources are devoted to it. For instance, in case of Coffee Junction, increasing the advertising expenditure may lead to higher revenue, but the marginal revenue (revenue generated by each additional dollar spent) will gradually decrease.
b) How much revenue will the company earn at that level of advertising spending?
At x = 1, the company will earn R(1) = -32 + 6 + 18 + 4 = -4,000 dollars.
c) What does 0≤x≤25 tell us with respect to this problem?
In this problem, 0 ≤ x ≤ 25 implies that the Coffee Junction company has the capacity to spend a maximum of 25,000 dollars per month on advertisements.
To learn more about marginal cost refer:-
https://brainly.com/question/14923834
#SPJ11
How many gallons equal 8 quarts?
2 gallons
4 gallons
12 gallons
32 gallon
Answers
its 2 gallons
4 would be 16
12 would be 48
32 would be 128