the perimeter of a one rectangular deck is 78 feet. the length of deck can be represented as (2x 3), and its width can be represented as (3x-4). the perimeter of a second rectangular deck is 2 times the perimeter of the first deck with a length of (4x 6) and a width of (6x -1). what is the value of x of the first rectangular deck?
Answers
The value of x of the first rectangular deck is 8.
For given question,
The perimeter of a one rectangular deck is 78 feet.
The length of the first rectangular deck is represented as (2x + 3), and its width is represented as (3x-4).
Similarly, the perimeter of a second rectangular deck is 2 times the perimeter of the first deck with a length of (4x + 6) and a width of (6x -1).
We need to find the value of x of the first rectangular deck.
Let P1 be the perimeter of the first rectangular deck.
⇒ P1 = 2 × (length + width)
⇒ 78 = 2 × [(2x + 3) + (3x - 4)]
⇒ 39 = (2x + 3x + 3 - 4)
⇒ 39 = 5x - 1
⇒ 40 = 5x
⇒ x = 40/5
⇒ x = 8
Therefore, the value of x of the first rectangular deck is 8.
Learn more about the perimeter of the rectangle here:
https://brainly.com/question/2142493
#SPJ4
Related Questions
solve
-7 2/3+(-5 1/2)+8 3/4
Answers
Answer:
4.416 and on going for example 4.41666666666
Which expression is equivalent to 3x + 2.5(4x + 2)?
A. 13x + 2
B. 13x + 5
C. 22x + 2
D. 22x + 5
Answers
Answer:
I think its B
Step-by-step explanation:
Hope this helps:)
The equivalent expression is,
⇒ 13x + 5
Option B is true.
What is an expression?
Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
The expression is,
⇒ 3x + 2.5 (4x + 2)
Now,
Simplify the expression as;
The expression is,
⇒ 3x + 2.5 (4x + 2)
⇒ 3x + 2.5 × 4x + 2.5 × 2
⇒ 3x + 10x + 5
⇒ 13x + 5
Thus, The equivalent expression is,
⇒ 13x + 5
Option B is true.
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ2
Please help me answer.

Answers
Answer:
Slope-intercept: y=3/4x+1
Sorry idk how to do general form
Step-by-step explanation:
Slope-intercept form is y=mx+b, m being the slope, b being the y-intercept.
The slope of this graph is 3/4, and the y-intercept is 1.
Answer:
Slope-intercept form: \(y=\frac{3}{4}x+1\)
General form: \(-3/4x+y-1\)
Step-by-step explanation:
Firstly, to get the slope intercept form, we need to find the slope and the y-intercept. To find the slope, we can use the slope formula and calculate the "rise over run" for these two points. The coordinate of the first point is (0, 1) , and the coordinate of the second point is (4, 4). If x1 = 0, x2 = 4, y1 = 1, and y2 = 4, we can plug those values into the slope formula that I mentioned earlier, which is \(\frac{y_{2}-y_{1}}{x_{2}-{x_{1}}}\). So, after we plug in those values we get in the two points, we can see that \(\frac{4-1}{4-0}\), so the slope is \(\frac{3}{4}\). The x moves right 4 times and the y goes up 3 times. Finally, the y-intercept value is 1 because when x = 0, y is 1, and the point we used for the slope formula (0, 1) proves that. For the slope-intercept form, \(mx+b\), where m is the slope and b is the y-intercept, m is \(\frac{3}{4}\) and b is 1. So, our final answer for the slope-intercept form is \(y=\frac{3}{4}x+1\). Now we can find the general form. To do this, we must get one side of the equation to equal 0. Using our slope-intercept equation, \(y=\frac{3}{4}x+1\), we can subtract y from both sides to get 0 on the left, like this: \(0=\frac{3}{4}x+1-y\). Then, we can rearrange the variables to general form: \(0=\frac{3}{4}x-y+1\\\). That is our general form answer. To recap, to find the slope, find the coordinates of the two points, and then plug in those points into the slope formula to find the steepness of the line. Then, add the y intercept that we can see on the graph. For general form, subtract y from both sides and rearrange the equation. Hope this helps!
3n-(2+n) ??????????????????????????
Answers
Answer:
2n - 2
Step-by-step explanation:
\(3n-(2+n)\\\\3n-2-n\\\\3n-n-2\\\\\boxed{2n-2}\)
Hope this helps.
3n - 2 - n
2n - 2
(b) Assume that the random variable X has the density function f
X
(x)=
⎩
⎨
⎧
−
34
3
x
2
+
34
15
x,
0,
1≤x≤3
otherwise
i. P(1.5
Answers
The probability that X lies between 1.5 and 2.5 is 119/45, calculated by integrating the given density function over the interval.
Given density function:
f(x) =
-34/3 * x^2 + 34/15 * x, 1 ≤ x ≤ 2,
0, elsewhere.
To find P(1.5 < X < 2.5), we integrate the density function over the interval [1.5, 2.5].
Step 1: Calculate the integral for the interval [1.5, 2]:
∫[1.5, 2] (-34/3 * x^2 + 34/15 * x) dx
Applying the antiderivative (integral) to each term:
= [-34/3 * (x^3/3) + 34/15 * (x^2/2)] evaluated from 1.5 to 2
= [-34/3 * (2^3/3) + 34/15 * (2^2/2)] - [-34/3 * (1.5^3/3) + 34/15 * (1.5^2/2)]
Simplifying further:
= [-34/3 * (8/3) + 34/15 * 2] - [-34/3 * (3^3/3) + 34/15 * (3^2/2)]
= (-272/9 + 68/15) - (-102/3 + 34/10)
= -272/9 + 68/15 + 102/3 - 34/10
= -136/45 + 68/15 + 340/45 - 34/10
= (68 - 136 + 340 - 153)/45
= 119/45
Step 2: Calculate the integral for the interval (2, 2.5]:
∫(2, 2.5] 0 dx
= 0
Step 3: Sum the probabilities of the two intervals:
P(1.5 < X < 2.5) = ∫[1.5, 2] (-34/3 * x^2 + 34/15 * x) dx + ∫(2, 2.5] 0 dx
= 119/45 + 0
= 119/45
Therefore, P(1.5 < X < 2.5) is equal to 119/45.
Learn more about Probability click here :brainly.com/question/30034780
#SPJ11
Show that Z is not isomorphic to Q. Warning: Z and Q have the same cardinality, so make sure you use algebra here it's required!
Answers
Z (the set of integers) is not isomorphic to Q (the set of rational numbers). To show that Z is not isomorphic to Q, we can use the fact that isomorphism preserves the algebraic structure of the sets.
Let's assume that there exists an isomorphism f: Z -> Q between the sets Z and Q. Since f is an isomorphism, it must preserve the operations of addition and multiplication.
However, we can observe that Z has an element 1 with the property that if we add it repeatedly, we can never reach the element 0. In other words, there is no integer n such that 1 + 1 + ... + 1 (n times) = 0.
On the other hand, Q does not have such an element. For any rational number q ≠ 0, we can find an integer n such that q^n = 0. This is because every non-zero rational number q can be expressed as q = p/q, where p and q are coprime integers, and we can choose n = q.
Therefore, the algebraic structure of Z (with respect to addition) is not preserved under the isomorphism with Q, which implies that Z is not isomorphic to Q.
To know more about isomorphism refer here:
https://brainly.com/question/32641367#
#SPJ11
A square has an area of 4x² - 121.
What is the length of each side?
Answers
Answer:
2x - 11, 2x + 11
Step-by-step explanation:
The length of each side must multiply together to get \(4x^2 - 121\) so have to factorise to make 2x-11 and 2x +11.
Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) 5x2 + 2x − 5/x3 − x dx
Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.)
3x2 − 20x + 33/
(2x + 1)(x − 2)2
dx
Answers
The solution to the integral is:
∫ (5x^2 + 2x - 5) / (x^3 - x) dx = 4 ln |x| + ln |x-1| - 5 ln |x+1| + C
The solution to the integral is:
∫ (3x^2 - 20x + 33) / [(2x + 1)(x - 2)^2] dx = (1/3) ln |2x + 1| - (64/25) ln |x - 2| - (49/100)/(x - 2) + C
Evaluating an integralFrom the question, we are to evaluate the given integral.
To evaluate the integral ∫ (5x^2 + 2x - 5) / (x^3 - x) dx, we can use partial fraction decomposition.
First, we factor the denominator:
x^3 - x = x(x^2 - 1) = x(x-1)(x+1)
So, we can write:
(5x^2 + 2x - 5) / (x^3 - x) = A/x + B/(x-1) + C/(x+1)
where A, B, and C are constants to be determined.
Multiplying both sides by the denominator (x^3 - x), we get:
5x^2 + 2x - 5 = A(x-1)(x+1) + B(x)(x+1) + C(x)(x-1)
Substituting x = 0, we get:
-5 = -A - B - C
Substituting x = 1, we get:
2 = 2B
So, B = 1.
Substituting x = -1, we get:
-8 = -2A
So, A = 4
Substituting these values back into the equation above and simplifying, we get:
(5x^2 + 2x - 5) / (x^3 - x) = 4/x + 1/(x-1) - 5/(x+1)
Hence, the integral becomes:
∫ [(5x^2 + 2x - 5) / (x^3 - x)] dx = 4 ln |x| + ln |x-1| - 5 ln |x+1| + C
where C is the constant of integration.
To evaluate the integral ∫ (3x^2 - 20x + 33) / [(2x + 1)(x - 2)^2] dx
First, we factor the denominator:
(2x + 1)(x - 2)^2 = (2x + 1)(x - 2)(x - 2)
So, we can write:
(3x^2 - 20x + 33) / [(2x + 1)(x - 2)^2] = A/(2x + 1) + B/(x - 2) + C/(x - 2)^2
Where A, B, and C are constants to be determined.
Multiplying both sides by the denominator (2x + 1)(x - 2)^2, we get:
3x^2 - 20x + 33 = A(x - 2)^2 + B(2x + 1)(x - 2) + C(2x + 1)
Substituting x = -1/2, we get:
49/4 = 25C
So, C = 49/100.
Substituting x = 2, we get:
3 = 9A
So, A = 1/3.
Substituting these values back into the equation above and simplifying, we get:
(3x^2 - 20x + 33) / [(2x + 1)(x - 2)^2] = 1/(3(2x + 1)) + B/(x - 2) + (49/100)/(x - 2)^2
To find B, we can take the derivative of both sides with respect to x:
d/dx [(3x^2 - 20x + 33) / [(2x + 1)(x - 2)^2]] = d/dx [1/(3(2x + 1)) + B/(x - 2) + (49/100)/(x - 2)^2]
Simplifying and evaluating at x = 2, we get:
-16/25 = -B/4
So, B = 64/25.
Substituting these values back into the equation above and simplifying, we get:
(3x^2 - 20x + 33) / [(2x + 1)(x - 2)^2] = 1/(3(2x + 1)) + (64/25)/(x - 2) + (49/100)/(x - 2)^2
Hence, the integral becomes:
∫ [(3x^2 - 20x + 33) / [(2x + 1)(x - 2)^2]] dx = ∫ [1/(3(2x + 1)) + (64/25)/(x - 2) + (49/100)/(x - 2)^2] dx
= (1/3) ln |2x + 1| - (64/25) ln |x - 2| - (49/100)/(x - 2) + C
Where C is the constant of integration
Learn more on Evaluating integrals here: https://brainly.com/question/28157330
#SPJ1
Which of the following quadratic regression equations best fits the data shown below?

Answers
Answer:
Step-by-step explanation:
In order to do this, you have to know how to use your calculator's regression equation function.
First enter in the data. Hit "stat" then 1:Edit and enter all the x values into L1. After each value, hit enter. When you're done with the x list, arrow over to L2 and enter in all the y-values. If there are already values there you need to clear, arrow up to highlight L1, hit "clear", then "enter" and the values will disappear. Do that for both lists if you need to.
After the data is listed in L1 and L2, hit "stat" again and arrow over to "Calc". Hit 5:QuadReg. If you have a TI 83, your equation will be there for you. If you have a TI 84, you'll need to arrow down to "calculate" to get the equation. Regardless, the equation is
\(y=3.48x^2+1.22x+3.44\), the last choice in your options.
Answer: D
Becasye I got it from him
The bearing of a boy on the corridor of a storey building from a ball on the ground is N72°E. What is the bearing of the ball from the boy?
Answers
Answer:
Step-by-step explanation:
man is standing in the corridor of a 10-storey building and looking down at a tall tree in front of the building. He sees the top of the tree at angle of depression of 30o. If the tree is 200m tall and the man's eyes are 300m above the ground, calculate the angle of depression of the foot tree as seen by the man
A. 30o
B. 60o
C. 45o
D. 25o
Explanation
Let x rep. the angle of depression of the foot of the tree.
tan 30o = y100y100
y = 100 tan 30o
= 57.8
By Pythagoras, AC2 = 3002 + 582
= 900 + 3354
tan x = oppadjoppadj
= 5830058300
= 0.19
tan x = 0.19
x = tan 0.19
= 60o
I need help desperately lol

Answers
Answer:
Step-by-step explanation:
First find the shaded area. Ignore the fact that something is missing.
L = 16
w = 8
Area = L*w Substitute the givens
Area = 16*8
Area = 128
Now consider the white area. It has a "length" of 4 and a width of 8
L = 4
w = 8
Area = 32
Now subtract 32 from 128
Area of shaded part = 128 - 32
Answer: 96 mm^2
For the following set of scores: 6, 2, 3, 0, 4 If these scores are a population, what are the variance and standard deviation?
Answers
Answer:
the population variance is 2 and the population standard deviation is approximately 1.41.
Step-by-step explanation:
To calculate the variance and standard deviation of a population, you can use the following formulas:
Population variance = (Σ(x - μ)²) / N
Population standard deviation = √(Σ(x - μ)² / N)
Where:
Σ is the sum of
x is each individual score in the population
μ is the population mean
N is the number of scores in the population
To begin, we need to find the population mean (μ):
μ = (6 + 2 + 3 + 0 + 4) / 5 = 3
Next, we can calculate the variance:
Population variance = ((6-3)² + (2-3)² + (3-3)² + (0-3)² + (4-3)²) / 5
Population variance = (9 + 1 + 0 + 9 + 1) / 5
Population variance = 2
Finally, we can calculate the standard deviation:
Population standard deviation = √((6-3)² + (2-3)² + (3-3)² + (0-3)² + (4-3)²) / 5
Population standard deviation = √(9 + 1 + 0 + 9 + 1) / 5
Population standard deviation = √2
Therefore, the population variance is 2 and the population standard deviation is approximately 1.41.
The variance of the given set of scores is 4 and the standard deviation is 2. Both are measures of how spread out the data is in statistics. The variance is calculated by acquiring the average squared deviation from the mean, while the standard deviation is the square root of the variance.
Explanation:This is a question about the notions of variance and standard deviation in statistics. Variance is a measure of how spread out the numbers in a data set are. Standard deviation, on the other hand, is the square root of the variance, indicating the amount of deviation (or variation) you can expect in your data.
Here are the steps for calculating variance and standard deviation for given set of scores: 6, 2, 3, 0, 4
To calculate the variance: Find the mean (average) of the data set: (6 + 2 + 3 + 0 + 4) / 5 = 3 Subtract the mean from each data point and square the result: (6-3)² = 9, (2-3)² = 1, (3-3)² = 0, (0-3)² = 9, (4-3)² = 1 Add up those squared results: 9 + 1 + 0 + 9 + 1 = 20 Divide by the number of data points: 20 / 5 = 4. So the variance (σ²) of this population is 4. To calculate the standard deviation: Take the square root of the variance: √4 = 2. Hence, the standard deviation (σ) of this population is 2. Learn more about Variance and Standard Deviation here:
https://brainly.com/question/32120727
#SPJ2
May someone please help me with this:)

Answers
Answer:
i think its 64
Step-by-step explanation:
Radius =2.
Height =4.
Pi=3.14.
V= 3.14(2)2(4).
Volume = 50 .24 cm^2
Please help, will give extra points

Answers
Answer:
59 degrees
Step-by-step explanation:
Since angle BGC is 40 degrees and angle AGC is 19 degrees and they are asking for angle AGB which is the sum of both angles together, you just add the 40 degrees plus 19 degrees.
(a)A line through (2,1) meets the curve x²-2x-y=3at A (-2,5)and at B. Find the coordinates of B
(b) A(3,1) lies on the curve (x-1)(y+1)=4. A line through A perpendicular to x+2y=7 meets the curve again at B. Find the coordinates of B.
Answers
The slope of the line passing through these two points is:
m = (y2 - y1) / (x2 - x1) = (1 - 5) / (2 - (-2)) = -4/4 = -1
Using the point-slope form of the equation of a line, the equation of the line passing through A and (2,1) is:
y - 5 = -1(x + 2)
y - 5 = -x - 2
y = -x + 3
To find the coordinates of point B, we need to solve the system of equations formed by the equation of the line and the equation of the curve:
x² - 2x - y = 3
y = -x + 3
Substituting the second equation into the first, we get:
x² - 2x - (-x + 3) = 3
x² - x - 6 = 0
Solving for x using the quadratic formula, we get:
x = (1 ± √(1 + 24)) / 2 = 3 or -2
When x = 3, y = -x + 3 = 0, which means that point B is (3,0).
When x = -2, y = -x + 3 = 5, which means that point B is (-2,5).
Therefore, the coordinates of point B are (3,0) and (-2,5).
(b) We know that point A (3,1) lies on the curve (x-1)(y+1)=4.
Substituting x=3 and y=1 into this equation, we get:
(3-1)(1+1) = 4
4 = 4
Therefore, point A satisfies the equation of the curve.
We need to find the equation of the line passing through point A that is perpendicular to the line x+2y=7.
The slope of the line x+2y=7 is:
m = -1/2
The slope of a line perpendicular to this line is the negative reciprocal, which is:
m' = 2
Using the point-slope form of the equation of a line, the equation of the line passing through A(3,1) with slope 2 is:
y - 1 = 2(x - 3)
y - 1 = 2x - 6
y = 2x - 5
To find the coordinates of point B, we need to solve the system of equations formed by the equation of the line and the equation of the curve:
(x-1)(y+1) = 4
y = 2x - 5
Substituting the second equation into the first, we get:
(x-1)(2x-4) = 4
2x³ - 6x² + 4x - 5 = 0
We can use numerical methods to solve this cubic equation to get the value of x, and then substitute it back into the equation y = 2x - 5 to get the value of y. One possible solution is:
x ≈ 2.632
y ≈ -0.736
Therefore, the coordinates of point B are approximately (2.632, -0.736).
Which situation can be represent by the equation 1.50x + 3.00 = 9.00
Answers
Answer: it’s Sara paid 3
Step-by-step explanation:
The situation can be represent by the equation 1.50x + 3.00 = 9.00
Sara paid $3 for a ticket to the carnival. Carnival ride cost $1.50 each. Sara rode x rides and spent a total of $9 at carnival.
What is Equation?Equations are mathematical statements with two algebraic expressions flanking the equals (=) sign on either side.
It demonstrates the equality of the relationship between the expressions printed on the left and right sides. LHS = RHS is a common mathematical formula.
Coefficients, variables, operators, constants, terms, expressions, and the equal to sign are some of the components of an equation. The "=" sign and terms on both sides must always be present when writing an equation.
Given:
1.50x + 3.00 = 9.00
Here we have 1.50x shows x is changing factor which has constant price 1.50.
and, $3 is the price of additional thing.
Then, the best option is Sara paid $3 for a ticket to the carnival. Carnival ride cost $1.50 each. Sara rode x rides and spent a total of $9 at carnival.
Learn more about Equation here:
https://brainly.com/question/29657992
#SPJ5
To hire an accountant to prepare taxes costs a flat fee and an additional hourty rate. The amount the accountant costs can be modeled by the function A(X) = 140 +
25x, where x represents the number of hours the accountant works to prepare the taxes and 140 represents the flat fee. What is the value of A(215) and its
interpretation?
a A(215) = 3; If the accountant takes 215 hours to prepare the taxes, the cost wil be $2.
b A(215) = 3; If the account takes 3 hours to prepare the taxes, the cost wil be $215.
c A(215) = 5515; If the accountant takes 215 hours to prepare the taxes, the cost wil be $5,515.
d A(215) = 5515; If the accountant takes 5,515 hours to prepare the taxes, the cost will be $215.
Answers
Answer: The given function is:
A(x) = 140 + 25x
We need to find the value of A(215), which means we need to substitute x = 215 in the function and simplify:
A(215) = 140 + 25(215)
A(215) = 140 + 5375
A(215) = 5515
Therefore, the correct answer is (c) A(215) = 5515. The interpretation of this result is that if the accountant works for 215 hours to prepare the taxes, the cost will be $5,515, which includes the flat fee of $140 and an additional hourly rate of $25 for each hour worked.
Step-by-step explanation:
The value of A(215) and its interpretation are captured thus:
A(215) = 5515; If the accountant takes 215 hours to prepare the taxes, the cost will be $5,515
What does the function represents?The function given as A(x) = 140 + 25x, represents the total cost of using the services of the accountants for tax computation and preparation, bearing in mind that the 140 means $140 which is the fixed charged irrespective of the number of hours it takes to prepare the tax returns whereas the 25x means that $25 is charged as variable fee for every hour the accountant works on the tax computation
A(x) = 140 + 25x
In this case, A(215) means that 215 hours were made use of by the accountants, hence, to determine the total fees, we simply substitute for x
A(215) = 140+(25*215)
A(215) = 140+5375
A(215)=$5,515
Find out more about professional fees on: https://brainly.com/question/28447174
What is they system of inequalities associated with the following graph?
Answers
Answer: We can find the inequalities. One inequality has a line with y-intercept 2 and slope -1. The inequality is y >= -x + 2.
Step-by-step explanation:
What is the domain of the ordered pairs shown in the graph?
{–2, –1, 0, 1}
{–2, –1, 0, 2}
{–1, 0, 1, 2}
{–2, 0, 2, 3}

Answers
Answer:
-2 0 2 3 this is the domain of the ordered pairs shown in the graph above
Find the rate of change in the graph

Answers
Answer:
4/3
hope this helped :)
The cylindrical water tank on a semitrailer has a length of 20 feet. The volume of the tank is equal to the product of pi, the square radius of the tank, and the length of the tank.
Let V represent the volume of the tank, r represent the radius of the tank, and h represent the length of the tank.
Part A.
Create an equation that could be used to find the volume, V, of the cylindrical tank.
Part B.
Rewrite the volume formula to create an equation that can be used to calculate the radius, R, of the water tank.
Drag the terms to the correct locations in the equation. Not all terms will be used.
\(r = \sqrt{ \frac{?}{?} } \)
20h, 20pi, 20V, V, 400(pi)h, i
Part C.
Graph the radical equation that can be used to calculate the radius, r, of the tank. Use lowercase "r" and the uppercase "V" when typing the equation.
Part D.
Suppose the cylindrical water tank has a radius of 12 feet. Use this information and the equation modeling the radius of the tank to complete these statements.
The volume of the water tank is about [4,000], [9,048], [754], or [2,880] cubic feet.
Answers
Answer:
Part A
V = π × r² × h
Part B
\(r = \sqrt{\dfrac{V}{\pi \times 20} }\)
Part C
The graph of the function created with MS Excel is attached
Part D
V ≈ 9,048
Step-by-step explanation:
The length of the cylindrical water tank = 20 feet
The volume of the tank, is given by the product of pi, and the square of the radius and the length of the tank
Where;
V = The volume of the tank
r = The radius of the tank
h = The length of the tank
Part A
The equation that could be used to find the volume of the tank, V, is given as follows;
V = π × r² × h
Part B
The equation that can be used to calculate the radius of the tank r is given by making r the subject of the volume of the cylindrcal tank as follows;
V = π × r² × h
r² = V/(π × h)
r = √(V/(π × 20))
Therefore;
\(r = \sqrt{\dfrac{V}{\pi \times h} } = \sqrt{\dfrac{V}{\pi \times 20} }\)
Part C
The graph of the equation is given as follows;
r; 0, 3, 6, 9, 12
V; 0, 565.5, 2261.95, 5,089.38, 9047.79
Please find attached the graph of the function created with MS Excel
Part D
When the radius is 12 feet, we get;
V = π × 12² × 20 ≈ 9047.79 ≈ 9,048

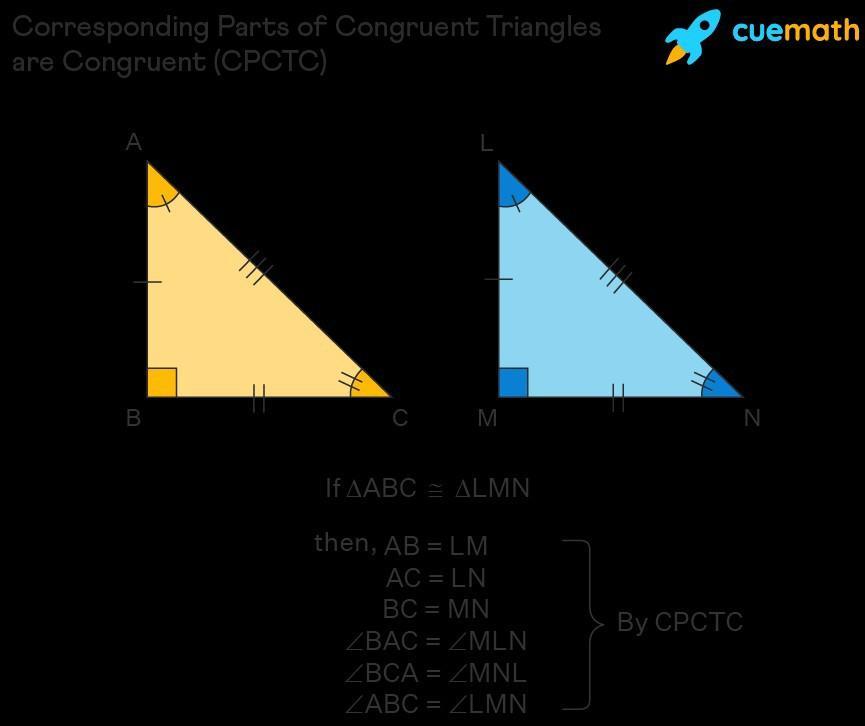
Can someone help me understand CPCTC for algebra please????
Answers
Answer:
The CPCTC theorem states that when two triangles are congruent, their corresponding parts are equal. The CPCTC is an abbreviation used for 'corresponding parts of congruent triangles are congruent'.
Expand and simplify
(4 + 2)(6-2)
Give your answer in the form b+ CV 2
Answers
Answer:
(4+2)(6-2)
24+8+12-4
44-4
40
Answer:
youre welcome- have a nice day
Step-by-step explanation:

I need help with 1-4

Answers
Answer:
the post looks blurry on my end, can you repost so i can help you
Step-by-step explanation:
I NEED HELP PLEASE A 25,000-mile steel band is placed around the earth, snugly fit at the equator. The band is cut, and 36 inches of string is spliced into the steel band. This new, larger circular band is placed around the earth, so its center coincides with the center of the earth, and a gap is created. How wide is this gap?
When you have finished, post your work showing the formula used for calculating the gap (g), show all calculations solving for g (gap), and a statement interpreting the results of your work.
Answers
The gap is approximately 259,854.9 inches wide.
What is the circumference of a circle?
The circumference of a circle is given by the formula C = 2πr, where C is the circumference and r is the radius of the circle.
The Earth's equator has a circumference of about 24,901 miles. The new circular band has a circumference of 25,036 inches.
When the steel band was cut and spliced, it increased the circumference by 36 inches. Since the circumference is directly related to the diameter, the new band is also larger in diameter than the original band.
We can use this increase in circumference to find the increase in diameter:
25,036 inches / 2π = 3957.1 inches
24,901 miles * 12 inches/mile = 298,812 inches
The gap is the difference between the two diameters:
298,812 inches - 3957.1 inches = 259,854.9 inches
Hence, The gap is approximately 259,854.9 inches wide.
To learn more about the circumference of a circle visit,
https://brainly.com/question/18571680
#SPJ1
Which of the following is a correct setup for integral S f(x, y, z) dS, where f(x, y, z) = xyz and S is the cylinder parametrized by the function r(u, v) = 2 cos u i + v j + 2 sin u k, with 0 ≤ u ≤ 2π and 3 ≤ v ≤ 6?
(a) integral 2π to 0 integral 6 to 3 (8v cos u sin u) dv du.
(b) integral 2π to 0 integral 6 to 3( 4v cos u sin u )dv du.
(c) integral 2π to 0 integral 6 to 3 (−4 cos u sin u) dv du.
(d) integral 2π to 0 integral 6 to 3 0 dv du.
(e) None of the other choices.
Answers
To set up the integral for the given function and surface, we need to calculate the cross product of the partial derivatives of the position vector r(u, v) and the function f(x, y, z). the correct setup is (b).
The correct setup for the integral is:
(b) integral 2π to 0 integral 6 to 3 (4v cos u sin u) dv du.
We can use the formula for the surface integral over a parametrized surface:
integral S f(x, y, z) dS = integral R f(r(u, v)) \(||r_u \times r_v||\ du\ dv\)
where R is the region in the uv-plane corresponding to the surface S, \(||r_u \times r_v||\) is the magnitude of the cross product of the partial derivatives of r with respect to u and v, and f(r(u, v)) is the function being integrated over the surface.
In this case, we have f(x, y, z) = xyz and r(u, v) = 2 cos u i + v j + 2 sin u k. The cylinder is defined by 0 ≤ u ≤ 2π and 3 ≤ v ≤ 6, so R is the rectangle in the uv-plane with those bounds.
To find \(||r_u \times r_v||\), we calculate the cross product of the partial derivatives:
\(r_u\) = -2 sin u i + 0 j + 2 cos u k
\(r_v\) = 0 i + 1 j + 0 k
\(r_u \times\ r_v\) = -2 cos u i - 0 j + 2 sin u k
\(||r_u \times r_v||=\sqrt((-2\ cos\ u)^2+0^2+(2\ sin\ u)^2)=2\)
So the integral becomes:
\(\int_{2\pi}^0\int_6^3\ f(r(u,v))\ ||r_u \times r_v||\ du\ dv\\\\\int_{2\pi}^0\int_6^3\ (2v\ cos\ u\ sin\ u)(2)\ dv\ du\\\\\int_{2\pi}^0\int_6^3\ (4v\ cos\ u\ sin\ u)\ dv\ du\)
Therefore, the correct setup is (b).
To know more about integral, visit:
https://brainly.com/question/31109342
#SPJ11
Triangle ABC and triangle QRS are similar and have the same orientation. The hypotenuse of triangle QRS is on the same line as the hypotenuse of triangle ABC and is four times the length of AB.
Answers
Part a) The slope of the hypotenuse of triangle ABC is Mab = -1.5
Part b) The coordinates of point R are (4,-7)
How do we calculate?Part a
The formula to calculate the slope between two points is equal to
m = y2- y1 / x2 - x1
The hypotenuse of triangle ABC is the segment AB
A(-6, 8) and B(-2, 2)
substituting the values, we have:
mab = -3/2
Part b)
triangle ABC and triangle QRS are similar which means that the ratio of its corresponding sides is proportional, the slope of its corresponding sides are congruent and its corresponding interior angles are congruent too.
so mQR = Mab
mQR = -3/2
we have
3/2 = y + 4/ x - 2
Q(2, -4) and R( x,y )
We have said that Triangle ABC and triangle QRS are the same orientation
so
The x-coordinate of R must be positive
The y-coordinate of R must be negative
Plot points A,B and Q to understand
therefore
----> -3 = y+ 4 ----> y-7
----> 2 = x- 2 ----> x = 4
The coordinates of point R are (4,-7)
Learn more about corresponding interior angles at: https://brainly.com/question/26167358
#SPJ1
#complete question:
Triangle ABC and triangle QRS are similar and are the same orientation. The endpoints of the hypotenuse of triangle ABC are A(-6, 8) and B(-2, 2). The hypotenuse of triangle QRS is on the same line as the hypotenuse of triangle ABC and is one-half the length of AB.
What is the slope of the hypotenuse of triangle ABC? __________________
What are the coordinates of the hypotenuse of triangle QRS? Q(2, -4) and R( _, _ )
How many real solutions are there if the value of k 0 *?
Answers
If k = 0, there is just one distinct solution, sometimes called a double solution.
What is meant by real solutions?Depending on the sign of the discriminant, a quadratic equation will always have one of three real solutions: 0, one, or two. Only 2 actual solutions exist if the discriminant is positive.
If you get to the finish with 0=0, it signifies that the left and right sides of the equation are equal to each other regardless of the values of the variables involved. As a result, the solution set for this equation is made up entirely of real numbers for each variable.
There is just one distinct solution, occasionally referred to as a double solution, if k = 0.
The graph shifts upward if k is greater than 0. The graph is moved downward if k is less than 0.
To learn more about real solutions refer to:
https://brainly.com/question/3419787
#SPJ4
1. Una escalera de 4 m de longitud se apoya sobre una pared vertical. Si la distancia entre la base de la escalera a la pared es de 2.5 m. ¿Cuál es la altura que tiene la escalera sobre la pared?
Answers
Answer:
puedes resolver de dos maneras si diste teorema de Pitágoras lo aplicas
hipotenusa al cuadrado = cateto 2 +cateto 2 ( el 2 significa al cuadrado)
sustituyes
hipotenusa= 4m
cateto= 2,5
hay que hallar el otro cateto que nos daría la altura a la que está la escalera
despejamos y tenemos
cateto 2= hip2 -cat2
cat2=(4)2-(2,5)2=
= 16-6,25=9,75
luego hallamos la raíz cuadrada de 9,75= 3,12
la altura a la que se encuentra es 3,12m
-si aun no diste Pitágoras podes representarlo en una hoja utilizando cm en lugar de metros( a escala). trazas el triángulo rectángulo la base te la da la distancia a la cual se encuentra la escalera de la pared es decir 2,5cm trazas la hipotenusa de 4cm de manera que coincida con el cateto opuesto , y mides el valor de este ,será de 3,12cm no olvides que la respuesta la debes dar en metros ya que es la unidad de medida que te da.
How do you find the vertex form of y=3x^25x3 by completing the quare? can you explain ALL the tep?
Answers
Answer:
Below
Step-by-step explanation:
To complete the square, the leading x^2 coefficient needs to be = 1 , so factor out a 3 to get
y = 3 ( x^2 + 5/3x ) +3 (I assumed it was a + sign between the terms)
Then take 1/2 of the 5/3 ( 5/6 ) , square it (25/36) , add it to the parentheses.... then subtract the amount you added (3 * 25/36) by doing this..... to have this :
y = 3 ( x^2 + 5/3 x + 25/36) - 3 * 25/36 +3 then simplify to
y = 3 ( x + 5/6)^2 + 11/12 Done.