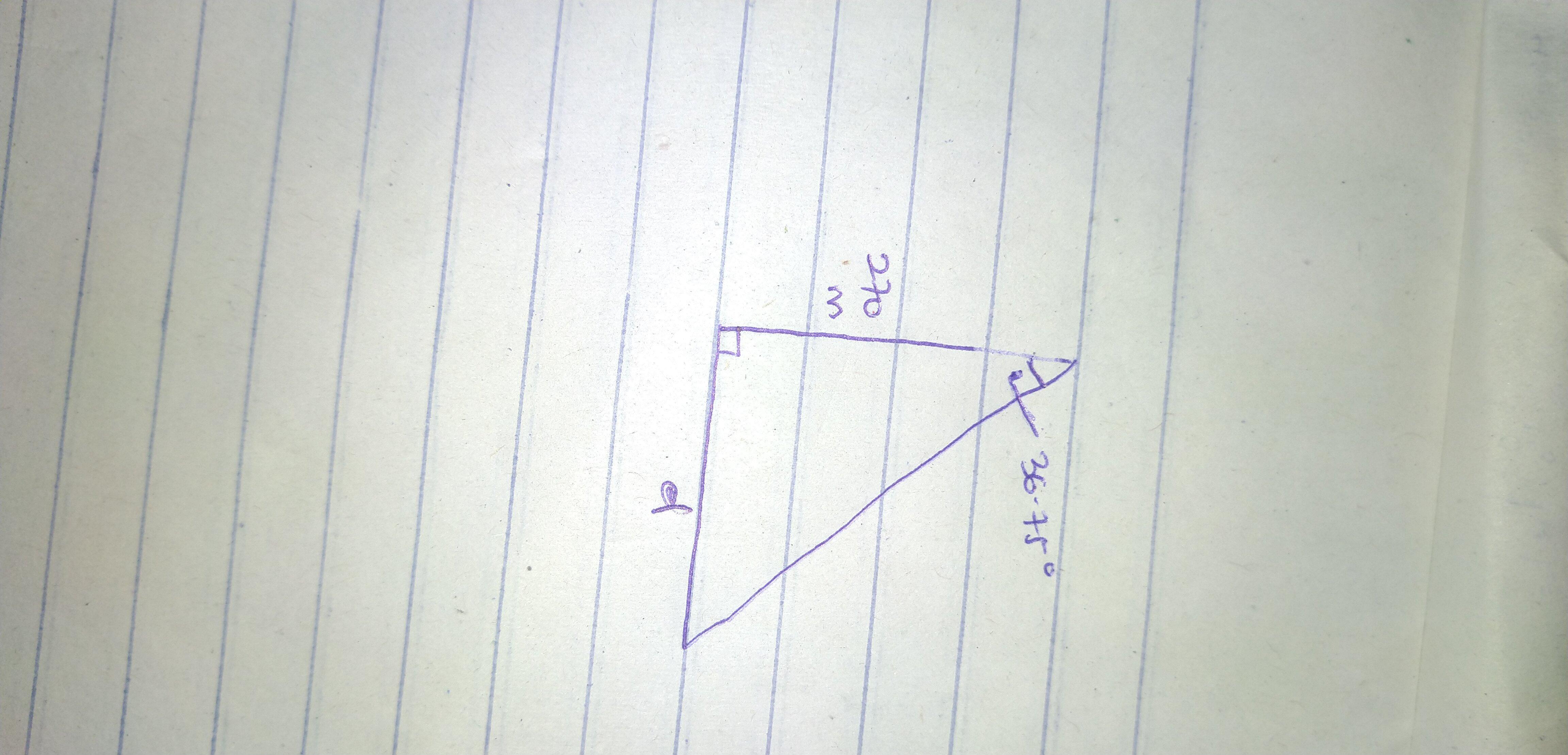
The measure of the angle of depression from the top of a 270-meter building to a park bench on the ground is 36°45′. How far away is the park bench from the building? Round to the nearest whole number.

Answer:

Y = -4x +(-6) is required answer ....

Based on the given assumptions and calculations, the net present value (NPV) of the investment in the new piece of equipment is -$27,045.76, indicating that the investment is not favorable.

To calculate the after-tax cash flows for each year and evaluate the investment decision, let's use the following information:

Assumptions:

Tax depreciation is straight-line over five years.

Pre-tax salvage value is $10,000 in Year 5 and $15,000 if the asset is scrapped in Year 4.

Tax on salvage value is 30% of the difference between salvage value and book value of the investment.

The cost of capital is 12%.

Given:

Initial investment cost = $50,000

Useful life of the equipment = 5 years

To calculate the depreciation expense each year, we divide the initial investment by the useful life:

Depreciation expense per year = Initial investment / Useful life

Depreciation expense per year = $50,000 / 5 = $10,000

Now, let's calculate the book value at the end of each year:

Year 1:

Book value = Initial investment - Depreciation expense per year

Book value \(= $50,000 - $10,000 = $40,000\)

Year 2:

Book value = Initial investment - (2 \(\times\) Depreciation expense per year)

Book value \(= $50,000 - (2 \times$10,000) = $30,000\)

Year 3:

Book value = Initial investment - (3 \(\times\) Depreciation expense per year)

Book value = $50,000 - (3 \(\times\) $10,000) = $20,000

Year 4:

Book value = Initial investment - (4 \(\times\) Depreciation expense per year)

Book value \(= $50,000 - (4 \times $10,000) = $10,000\)

Year 5:

Book value = Initial investment - (5 \(\times\) Depreciation expense per year)

Book value \(= $50,000 - (5 \times $10,000) = $0\)

Based on the assumptions, the salvage value is $10,000 in Year 5.

If the asset is scrapped in Year 4, the salvage value is $15,000.

To calculate the tax on salvage value, we need to find the difference between the salvage value and the book value and then multiply it by the tax rate:

Tax on salvage value = Tax rate \(\times\) (Salvage value - Book value)

For Year 5:

Tax on salvage value\(= 0.30 \times ($10,000 - $0) = $3,000\)

For Year 4 (if scrapped):

Tax on salvage value\(= 0.30 \times ($15,000 - $10,000) = $1,500\)

Now, let's calculate the after-tax cash flows for each year:

Year 1:

After-tax cash flow = Depreciation expense per year - Tax on salvage value

After-tax cash flow = $10,000 - $0 = $10,000

Year 2:

After-tax cash flow = Salvage value - Tax on salvage value

After-tax cash flow = $0 - $0 = $0

Year 3:

After-tax cash flow = Salvage value - Tax on salvage value

After-tax cash flow = $0 - $0 = $0

Year 4 (if scrapped):

After-tax cash flow = Salvage value - Tax on salvage value

After-tax cash flow = $15,000 - $1,500 = $13,500

Year 5:

After-tax cash flow = Salvage value - Tax on salvage value

After-tax cash flow = $10,000 - $3,000 = $7,000

Now, let's calculate the net present value (NPV) using the cost of capital of 12%.

We will discount each year's after-tax cash flow to its present value using the formula:

\(PV = CF / (1 + r)^t\)

Where:

PV = Present value

CF = Cash flow

r = Discount rate (cost of capital)

t = Time period (year)

NPV = PV Year 1 + PV Year 2 + PV Year 3 + PV Year 4 + PV Year 5 - Initial investment

Let's calculate the NPV:

PV Year 1 \(= $10,000 / (1 + 0.12)^1 = $8,928.57\)

PV Year 2 \(= $0 / (1 + 0.12)^2 = $0\)

PV Year 3 \(= $0 / (1 + 0.12)^3 = $0\)

PV Year 4 \(= $13,500 / (1 + 0.12)^4 = $9,551.28\)

PV Year 5 \(= $7,000 / (1 + 0.12)^5 = $4,474.39\)

NPV = $8,928.57 + $0 + $0 + $9,551.28 + $4,474.39 - $50,000

NPV = $22,954.24 - $50,000

NPV = -$27,045.76

The NPV is negative, which means that based on the given assumptions and cost of capital, the investment in the new piece of equipment would result in a net loss.

Therefore, the investment may not be favorable.

Please note that the calculations above are based on the given assumptions, and additional factors or considerations specific to the business should also be taken into account when making investment decisions.

For similar questions on assumptions.

https://brainly.com/question/15424356  

#SPJ8

The complete question may be like :

Assumptions: Tax depreciation is straight-line over five years. Pre-tax salvage value is $10,000 in Year 5 and $15,000 if the asset is scrapped in Year 4. Tax on salvage value is 30% of the difference between salvage value and book value of the investment. The cost of capital is 12%.

You are evaluating an investment in a new piece of equipment for your business. The initial investment cost is $50,000. The equipment is expected to have a useful life of five years.

Using the given assumptions, calculate the after-tax cash flows for each year and evaluate the investment decision by calculating the net present value (NPV) using the cost of capital of 12%.

The expression that has no solution is (b)  {x | x < 0} and {x | x > 0}

From the question, we have the following parameters that can be used in our computation:

{xlx≤0) or (x|x ≥ 0}

{x1x<0] and {x|x>0}

{x|x ≤0) and {x|x20]

Express the inequality expressions properly

So, we have

{x l x ≤ 0} or (x | x ≥ 0}

{x | x < 0} and {x | x > 0}

{x | x ≤ 0} and {x | x < 0}

Interpreting the option (b), we have

{x | x < 0} and {x | x > 0}

This means that x is less than 0 and x is greater than 0

This combination is not possible and it is a null set

Hence, the required expression is (b)

Read more about inequality at

https://brainly.com/question/25275758

#SPJ1

Lamoooo

Step-by-step explanation:

Answer:

40% x $80.00 = $32.00

$32.00 x 7% = $2.24

Step-by-step explanation:

$2.24

Lance needs to jog for an additional 316.08-25.5 = 290.58  minutes to burn 380 Calories.          

The information given in the table to  produce a direct equation that relates the number of Calories burned to the time spent jogging. Let's use the  pitch- intercept form y =  mx b, where y represents the number of Calories burned( in hundreds), x represents the time spent jogging( in  twinkles), m represents the rate of Calories burned( in hundreds per  nanosecond), and b represents the  original Calories burned( in hundreds).  To find m, we can use the points( 10, 13) and( 15, 19), which represent two ordered  dyads on the line. We can find the  pitch of the line using the  pitch formula  

m = ( y2- y1)/( x2- x1)  m = ( 19- 13)/( 15- 10)  

m = 1.2  So the equation for the line is  y = 1.2 x b.

 To find b, we can use the point

( 10, 13)  = 1.2( 10) b  b = 0.7

 So the complete equation for the line is  y = 1.2 x0.7  Now we can use this equation to  break for x, the number of  twinkles Lance needs to jog to burn 380 Calories.  

380 = 1.2 x0.7  = 1.2 x  x = 316.08

So Lance needs to jog for an additional 316.08-25.5 = 290.58  minutes to burn 380 Calories.

To know more about Additional .

https://brainly.com/question/4721701

#SPJ11

Answer:

90% of 300 = .90 × 300 = 270 high- definition televisions on order.

Answer:

49 square inches

Step-by-step explanation:

Length x width =area

since it is a square, all sides have a length of 7 inches

7x7=49 inches ^2

Answer:

parallel

Step-by-step explanation:

Answer:

140

Step-by-step explanation:

The statement "Every set can be considered a class" means that every object in set theory, including sets, can be considered a class. This is because classes are simply collections of objects, and sets are a type of collection.

The statement "If S is a set, consider the formula x S and the class {x: x = S}" means that if S is a set, then we can consider the formula x S, which states that x is an element of S, and the class {x: x = S}, which is the class of all objects that are equal to S.

In other words, the statement is saying that every set can be considered a class, and that we can define a class for any set by considering the formula that defines the set and the class of all objects that satisfy that formula.

For example, the set {1, 2, 3} can be considered a class by considering the formula x ∈ {1, 2, 3}, which states that x is an element of the set {1, 2, 3}, and the class {x: x ∈ {1, 2, 3}} is the class of all objects that are elements of the set {1, 2, 3}. This class is equal to the set {1, 2, 3}.

Learn more about set on

https://brainly.com/question/13458417

#SPJ1

9514 1404 393

Answer:

  x = 19

Step-by-step explanation:

The two marked angles are corresponding angles, so have the same measure.

  6x -9 = 5x +10

  x = 19 . . . . . . . . . add 9-5x

Answer:

The margin of error is of 0.7123 hours.

Step-by-step explanation:

We have that to find our \(\alpha\) level, that is the subtraction of 1 by the confidence interval divided by 2. So:

\(\alpha = \frac{1-0.9}{2} = 0.05\)

Now, we have to find z in the Ztable as such z has a pvalue of \(1-\alpha\).

So it is z with a pvalue of \(1-0.05 = 0.95\), so \(z = 1.645\)

Now, find the margin of error M as such

\(M = z*\frac{\sigma}{\sqrt{n}}\)

In which \(\sigma\) is the standard deviation of the population and n is the size of the sample.

Find the margin of error for a confidence interval for the population mean with a 90% confidence level.

We have that \(\sigma = 1.5, n = 12\). So

\(M = 1.645*\frac{1.5}{\sqrt{12}} = 0.7123\)

The margin of error is of 0.7123 hours.

Answer:

0.526

Step-by-step explanation:

To find the margin of error we need to identify three things: the z-score, σ, and n.

1.Find zα2 using invNorm. The invNormfunction has one input: probability.

Here, α=1−0.90=0.10. Probability is then 1−0.102=0.95. To find our z-score, we select invNorm after pressing 2nd then VARS. Type invNorm(0.95). The output Is 1.6448. This is the z-score.

2. σ=1.5.

3. n=22.

4. We type 1.6448×1.522√ on the calculator. The output is 0.526, when rounded to three decimal places. This is the margin of error.

Part 1

The equation is \(y=a(x+8)(x-72)\).

Using the point \((62, -490)\) to solve for \(a\),

\(-490=a(62+8)(62-72) \implies a=\frac{7}{10}\\\\\therefore \boxed{y=\frac{7}{10}(x+8)(x-72)}\)

Part 2

When \(x=-8\), \(y=0\).

When \(x=2\), \(y=-490\).

So, the average rate of change is \(\frac{-490-0}{2-(-8)}=\boxed{-49}\)

Based on the information we can infer that the equation shown in the image is 1.23 - 0.35 = 0.88 (option B).

To identify the correct equation we must look at the graph and identify the information it provides. In this case we have two squares divided into 100 squares each. Additionally, the square on the left has 88 squares painted in red and 12 squares with an X inside. In the case of the square on the right, it has 23 squares colored in red with an X inside.

In total we have 123 squares painted in red, which in decimal number is equivalent to 1.23. On the other hand, the number of squares painted red and with an X inside is 35, this value would be 0.35.

On the other hand, the squares painted only in red are 88, so the equivalent in decimal numbers would be 0.88. Therefore, the correct way to express this relationship through an equation would be:

Learn more about equations in: https://brainly.com/question/29538993

#SPJ1

Answer:

200

Step-by-step explanation:

Answer:

200

Step-by-step explanation:

Google told me that 20% of 1000 is 200

It will cost $1080 to paint all the interior surfaces of the pool.

6. & 7. The triangles have sides of 8, 8, and 10 cm, and an area of 24 square cm. The remaining areas are 18 and 12 square cm, respectively.

Triangle with Sides 8, 8, and 10 cm: First, we must calculate the area of the whole triangle, which has sides of 8, 8, and 10 cm. Using the Heron's formula, we can find the area of a triangle given the lengths of its sides: A = √(s(s - a)(s - b)(s - c)), where s = (a + b + c)/2 is the semi perimeter of the triangle.

A = √(13(13 - 8)(13 - 8)(13 - 10)) = √(13(5)(5)(3)) = √(2925) = 15√(65) ≈ 59.17 square cm. Next, we can calculate the areas of the shaded regions as follows: Area of Shaded Region 1 = Area of Whole Triangle - Area of Small Triangle Area of Shaded Region 1 = 15√(65) - 18 = 15√(65) - 6√(65) = 9√(65) ≈ 27.94 square cm.

Area of Shaded Region 2 = Area of Whole Triangle - Area of Large Triangle Area of Shaded Region 2 = 15√(65) - 24 = 3√(65) ≈ 7.74 square cm.7.

A swimming pool has the dimensions 8 m (length), 6 m (width), and 1.5 m (depth). The total area to be painted is the sum of the areas of the floor, the ceiling, and the walls of the pool. Since the pool is rectangular in shape, we can break it down into six different parts: the top and bottom surfaces, and the four vertical surfaces.

Let's begin by calculating the area of the floor, which has dimensions of 8 m by 6 m:Area of Floor = length x width = 8 x 6 = 48 square meters.

Next, we can calculate the area of the ceiling, which has the same dimensions as the floor: Area of Ceiling = length x width = 48 square meters. Since the pool has a depth of 1.5 m, the total height of the vertical surfaces is 1.5 x 2 = 3 m (since there are two vertical surfaces on each side of the pool).

Thus, the total area of the four vertical surfaces is given by: Area of Walls = perimeter x height = 2(length + width) x height = 2(8 + 6) x 3 = 84 square meters.

Finally, we can calculate the total area to be painted by adding up the area of the floor, ceiling, and walls: Total Area = Area of Floor + Area of Ceiling + Area of Walls Total Area = 48 + 48 + 84 = 180 square meters.

The cost of paint is given as $6 per square meter, so we can calculate the total cost of painting the pool as follows: Cost = Total Area x Cost per Square Meter Cost = 180 x $6 = $1080. Therefore, it will cost $1080 to paint all the interior surfaces of the pool.

For more such questions on dimensions

https://brainly.com/question/29755536

#SPJ8

The multiplication expression involving exponents with a product of 8 over 13 will be 8⁵ x 8⁸.

The analysis of mathematical representations is algebra, and the handling of those symbols is logic.

For example, 5³ = 5² x 5 here we separate 5³ into 5² and 5 so it is called the law of indices.

The multiplication expression involving exponents with a product of 8 over 13 will be given as,

⇒ 8¹³

By the law of indices that \(\rm x^c = x^a + x^b\) such that c = a + b.

⇒ 8⁵ x 8⁸

The multiplication expression involving exponents with a product of 8 over 13 will be 8⁵ x 8⁸.

More about the Algebra link is given below.

https://brainly.com/question/953809

#SPJ1

13,305 years

Step-by-step explanation:

\(A = A_02^{-\frac{t}{5730}}\)

Since only 20% of the original C-14 is left, then \(A=0.2A_0\). We can then write

\(0.2A_0=A_02^{-\frac{t}{5730}}\)

Taking the log of both sides,

\(\log 0.2 = \left(-\dfrac{t}{5730}\right)\log 2\)

Solving for t,

\(t = \dfrac{-(5730\:\text{years})\log 0.2}{\log 2}\)

\(\:\:\:\:\:\:\:= 13,305\:\text{years}\)

The required length of the base of the triangular pane of glass is 22 inches.

We know that the formula for the area of a triangle is:

Area = 1/2 * base * height

We are given that the height of the triangular pane of glass is 32 inches and the area is 352 square inches. Substituting these values into the formula, we get:

352 = 1/2 * base * 32

Multiplying both sides by 2 and dividing by 32, we get:

base = 22

Therefore, the length of the base of the triangular pane of glass is 22 inches.

Learn more about triangles here:
https://brainly.com/question/2773823

#SPJ1

Answer:

0 3/4

Step-by-step explanation:

Answer:

3/4 is a proper fraction

Step-by-step explanation:

it can not be a mixed number

Answer:

I think A, but if not I am soooooo sorry

Answer:

5 < x

Step-by-step explanation:

I just learned this stuff in class yw

Sofia's account balance in 7 years will be $11,726.12

From the question, we are to determine Sofia's account balance in 7 years

Using the compound interest formula,

\(A = P(1+ \frac{r}{n} )^{nt}\)

Where A is the amount

P is the principal

r is the rate

n is the number of times compounded

and t is the time in years

From the given information,

P = $8,000

r = 5.5% = 0.055

n = 4

t = 7

Putting the parameters into the equation, we get

\(A = 8000(1+ \frac{0.055}{4} )^{4\times 7}\)

\(A = 8000 ( 1+ 0.01375)^{28}\)

\(A = 8000 ( 1.01375)^{28}\)

A = $11,726.12

Hence, Sofia's account balance in 7 years will be $11,726.12

Learn more on Compound interest here: https://brainly.com/question/24924853

#SPJ1

The included angle of one triangle are congruent to the corresponding parts of the other triangle. Since the sides AD and BE are congruent, as well as the included angle DAB and CBA, then △ADE≅△BCE.

By the Side-Angle-Side (SAS) congruence theorem, if two sides and the included angle of one triangle are congruent to the corresponding parts of the other triangle, then the triangles are congruent. In this proof, the given statements provide that the sides AE and EB are congruent, as well as the angles DAB and CBA. This means that the two corresponding sides of the triangles △ADE and △BCE are congruent, and the included angles of the triangles are also congruent. Therefore, according to the SAS congruence theorem, the two triangles are congruent, and thus △ADE≅△BCE.

The SAS congruence theorem applies to any two triangles, regardless of the size or shape of the triangles. The congruence of the sides and angles is sufficient to prove that two triangles are congruent. This theorem can be used to prove other theorems, such as the Triangle Sum Theorem, which states that the sum of the angles in a triangle is equal to 180 degrees. To prove this theorem, one could use the SAS congruence theorem to show that two right triangles are congruent, and then use the congruent angles to prove that the sum of the angles in a triangle is 180 degrees.

Learn more about angle here

https://brainly.com/question/28451077

#SPJ1

Answer:

I think its flat sorry if it's wrong

Answer:

x<2

Step-by-step explanation:

2x+6<10

2x<10-6

2x<4

x<4/2

x<2

Answer:

5/4

Step-by-step explanation:

We can start but setting the blank as x.

x - 1/2 = 3/4

we can put a common denominator on both of the.

2, 4

4, 8

4 is a common denominator.

1/2 times 2/2 = 2/4

x - 2/4 = 3/4

add on both sides.

x = 5/4

Answer:

5/4

Step-by-step explanation:

____ - 1/2= 3/4

____= 3/4+1/2

= 3+2/4 ( LCM of 2,4 is 4)

5/4

Check

5/4-1/2=3/4