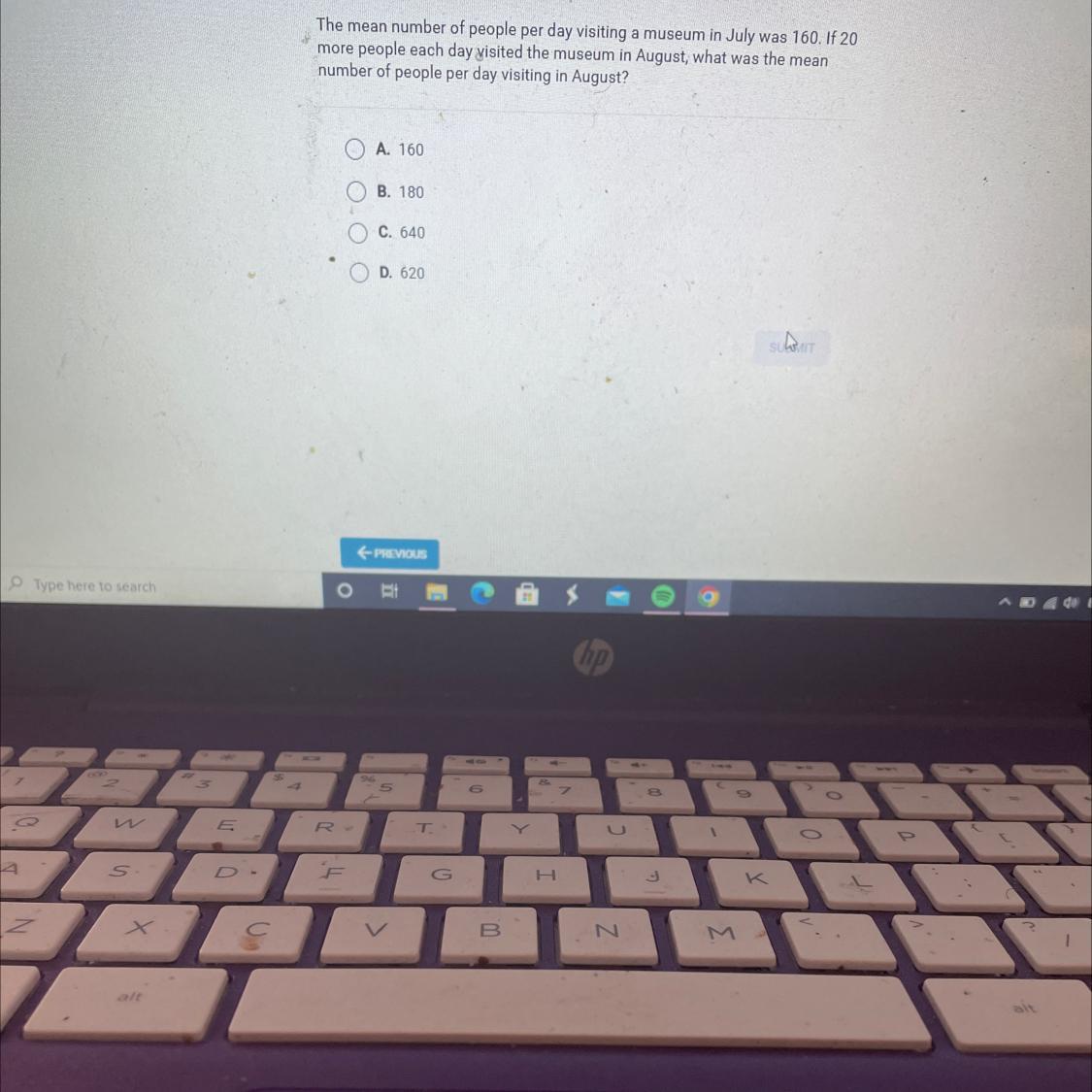
The mean number of people per day visiting a museum in July was 160. If 20more people each day visited the museum in August, what was the meannumber of people per day visiting in August?• A. 160B. 180640620
Answers
The given information is:
- The mean number of people visiting the museum in July was 160
- In August, each day 20 more people each day visited the museum.
The mean of a set of numbers is given by:
\(Mean=\frac{\text{ Sum of all data points}}{\text{ Number of data points}}\)July has 31 days, so the number of data points is 31, then the sum of all data points is:
\(\begin{gathered} 160=\frac{sum}{31} \\ \\ Sum=160*31=4960 \end{gathered}\)Now, August has 31 days too, and if each day 20 more people visited the museum, then we need to add to the sum of data points of July, 31*20, so:
\(August\text{ }sum=4960+31*20=4960+620=5580\)So, the mean in August is:
\(Mean=\frac{5580}{31}=180\)The answer is B. 180
Related Questions
What is the range of function g if g(x)=-2f(x)+1
Answers
The range of g is bounded between 1 - 2M and 1, but it may not include all values in that interval, depending on the range of f.
The range of function g depends on the range of the function f.
Let's start by assuming that we know the range of f.
If the range of f is Rf, then the range of -2f is the set {-2y | y ∈ Rf}, which is just the set of all numbers that can be obtained by multiplying an element of Rf by -2.
Finally, we add 1 to each of these values to get the range of g. Therefore, the range of g is:
Rg = {1 - 2y | y ∈ Rf}
In other words, the range of g is obtained by taking the range of f, multiplying each element by -2, and adding 1 to each result.
If we don't know the range of f, we can still say something about the range of g. Specifically, we know that g(x) can never be greater than 1 (since the largest value that -2f(x) can take is 0, and adding 1 to 0 gives us 1), and g(x) can never be less than 1 - 2M, where M is the largest possible value that f(x) can take on. In other words, the range of g is bounded between 1 - 2M and 1, but it may not include all values in that interval, depending on the range of f.
for such more question on range
https://brainly.com/question/16444481
#SPJ11
the bottom angle is also 45 could some one answer this for me

Answers
The length of the side opposite to the reference angle is 7.77 units.
What are trigonometric ratios in terms of a right-angle triangle?We know a right-angled triangle has three sides they are -: Hypotenuse,
Opposite and Adjacent.
We can remember SOH CAH TOA which is,
sin = opposite/hypotenuse, cos = adjecen/hypotenuse and
tan = opposite/adjacent.
If we take the reference angle 45°, The side 'x' is opposite and the side having a length of 11 units is the hypotenuse.
We know, sin = opposite/hypotenuse.
Therefore,
sin45° = x/11.
1/√2 = x/11.
x = 11/√2.
x = 7.77 units.
learn more about trig ratios here :
https://brainly.com/question/14977354
#SPJ1
What are the coordinates of point A' after translating point A 8 units down and 7 units right?
Answers
You didn’t put any starting coordinates, but you can just subtract 8 from the y coordinate since it is translated down, and add 7 to the x coordinate since it is moving to the right :) hope this helps
A bag contains 8 green candies and 4 red candies. You randomly select one candy at a time to eat. If you eat five candies, there are relatively prime positive integers m and n so that m n is the probability that you do not eat a
green candy after you eat a red candy. Find m + n.
Answers
If m/n is the probability that you do not eat green candy after you eat a red candy, then m + n is 6.
A bag contains 8 green candies and 4 red candies. If you eat five candies, there are relatively prime positive integers m and n so that m/n is the probability that you do not eat green candy after you eat a red candy. Below list the ways to accomplish this ordering along with their respective probabilities:
GRRRR : \(\frac{8}{12}\times\frac{4}{11} \times\frac{3}{10} \times\frac{2}{9} \times\frac{1}{8}\)
GGRRR : \(\frac{8}{12}\times\frac{7}{11} \times\frac{4}{10} \times\frac{3}{9} \times\frac{2}{8}\)
GGGRR : \(\frac{8}{12}\times\frac{7}{11} \times\frac{6}{10} \times\frac{4}{9} \times\frac{3}{8}\)
GGGGR : \(\frac{8}{12}\times\frac{7}{11} \times\frac{6}{10} \times\frac{5}{9} \times\frac{4}{8}\)
GGGGG : \(\frac{8}{12}\times\frac{7}{11} \times\frac{6}{10} \times\frac{5}{9} \times\frac{4}{8}\)
The sum is \(\frac{8\times3\times4(2+14+42+70+70)}{12.11.10.9.8}\)
Probability that you do not eat green candy after you eat a red candy =\(\frac{1}{5}\)
so m = 1 and n = 5
m + n =6
To know more about Probability.
https://brainly.com/question/16506016
#SPJ4
which of the following ordered pair make this equation true

Answers
Given:
y=2x+4
Required:
To calculate which pair makes the equation true
Explanation:
\(\begin{gathered} y=2x+4 \\ \\ let\text{ us place the value \lparen3,10\rparen at the place of x and y} \\ \\ x=3\text{ and y =10} \\ \\ 10=2(3)+4 \\ \\ 10=6+4 \\ \\ 10=10 \end{gathered}\)Required answer:
Option B (3,10)
Plz help I need with question I give thanks

Answers
Answer:
I believe X = 8
Step-by-step explanation:
you would use the equation D + C = B or
48 + 5x + 11 = 11x + 11
then subtract 11 from each side leaving
48 + 5x = 11x
then you would subtract 5x from each side, leading to
48 = 6x
48 ÷ 6 = 8
A football team charges $30 per ticket and averages 20,000 people per game. Each person spend an average of $8 on concessions.For everydrop of $1 in price,the attendance rises by 800 people.What ticket price should the team charge to maximize total revenue? Calculate the TR max.
Answers
The ticket price that would maximize the total revenue would be $ 23.
Given that a football team charges $ 30 per ticket and averages 20,000 people per game, and each person spend an average of $ 8 on concessions, and for every drop of $ 1 in price, the attendance rises by 800 people, to determine what ticket price should the team charge to maximize total revenue, the following calculation must be performed:
20,000 x 30 + 20,000 x 8 = 760,000 24,000 x 25 + 24,000 x 8 = 792,000 28,000 x 20 + 28,000 x 8 = 784,000 26,000 x 22.5 + 26,000 x 8 = 793,000 27,200 x 21 + 27,200 x 8 = 788,000 26,400 x 22 + 26,400 x 8 = 792,000 25,600 x 23 + 25,600 x 8 = 793,600 24,800 x 24 + 24,600 x 8 = 792,000
Therefore, the ticket price that would maximize the total revenue would be $ 23.
Learn more in https://brainly.com/question/7271015
please help!! find the inverse of image attached :)

Answers
The correct answer is option A: "If x doesn't equal 3, then 2x + 5 doesn't equal 11."
What is inverse?More precisely, if f is a function that maps elements from a set A to elements in a set B, then the inverse function of f, denoted as f^(-1), is a function that maps elements in set B back to elements in set A.
According to question:The given statement is: "If x equals 3, then 2b + 5 equals 11."
To find the inverse, we negate both the hypothesis and the conclusion of the statement and switch their order:Inverse: If x does not equal 3, then 2b + 5 does not equal 11.Therefore, the correct answer is option A: "If x doesn't equal 3, then 2x + 5 doesn't equal 11."
The inverse function f^(-1) is defined such that f(f^(-1)(x)) = x for all x in B, and f^(-1)(f(x)) = x for all x in A. In other words, applying the inverse function to the output of the original function returns the input value.
The existence of an inverse function depends on the properties of the original function. For example, a function must be one-to-one (or injective) to have an inverse function, which means that each input maps to a unique output. If a function is not one-to-one, then its inverse function may not exist or may have limited domain and range.
To know more about inverse visit:
https://brainly.com/question/30194642
#SPJ1
a = 18t + 5 4) Leo made an initial deposit to a savings account. Each week thereafter, he deposited a fixed amount into the account. The equation above models the amount, a, in dollars, that Leo has deposited after t weekly deposits. According to the model, how many dollars was Leo's initial deposit? (Disregard the $ sign when gridding your answer.) 5 6 8 9

Answers
According to the model, Leo's initial deposit was $0
According to the model, how many dollars was Leo's initial deposit?The model is given as
a = 18t + 5
When he makes his initial deposit, the value of t is
t = 0
i.e. this represents his balance before he starts saving on a weekly basis
Substitute 0 for t in the equation a = 18t + 5
So, we have
a = 18 * 0 + 5
Evaluate
a = 5
Hence, Leo's initial deposit was $0
Read more about linear functions at:
https://brainly.com/question/15602982
#SPJ1
Which of the following represents the factorization of the trinomial below?
x2 +9x - 22
O A. (x+20)(x - 2)
O B. (x+11)(x - 2)
O C. (x - 11)(x - 2)
O D. (x-20)(x-2)
Answers
doesn’t equal to x2+9x-22. Let’s check choice c you get x2-2x-11x+22 that doesn’t give us x2+9x-22 . You can also directly cross out choice d . Only b is the correct answer.
Bone-shaped treats are 5 for $3.50 at Shelley’s store and Sarah wants to buy 12. She set up and solved this proportion to find how much they would cost. Describe her error and find the correct solution.
5
3.5
=
12
x
3.5x = 60
x = $17.14
Answers
Answer:
Sarah multiplied the denominator by the denominator and the numerator by the numerator instead of finding the cross products. The equation should be 5x = 42, so the cost should be $8.40.
Step-by-step explanation:
Can I get brainliest?
in a classroom there are 28 tablets which includes 5 that are defective. if seven tablets are chosen at random to be used by student groups. 12. how many total selections can be made? a. 140 b. 98280 c. 11793600 d. 4037880 e. 1184040 13. how many selections contain 2 defective tablets? a. 10 b. 21 c. 336490 d. 706629 e. 33649
Answers
Using the combination formula, it is found that:
The number of total selections that can be made is: e. 1184040.The number of selections that contain two defective tablets is: c. 336490.Combination formula\(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula, involving factorials. It is used when the order in which the elements are chosen does not matter.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
In the context of this problem, we have that seven tablets are chosen from a set of 28 tablets, hence the number of selections that can be made is given by:
\(C_{28,7} = \frac{28!}{7!21!} = 1,184,040\)
For two defective tablets, the selections are given as follows:
Two defective from a set of five.Five non-defective from a set of 23.Hence the number of selections is calculated as follows:
\(C_{23,5}C_{5,2} = \frac{23!}{5!18!} \times \frac{5!}{2!3!} = 336,490\)
A similar problem, also about the combination formula, is given at https://brainly.com/question/25821700
#SPJ1
Find a value for y for which the expression (1-y)(3-y)(6-y) has each given value
i. -70
ii. 120
Answers
\(\\ \tt\Rrightarrow (1-y)(3-y)(6-y)=-70\)
\(\\ \tt\Rrightarrow -y(1+1)(3+1)(6+1)=-70\)
\(\\ \tt\Rrightarrow y(2)(4)(7)=70\)
\(\\ \tt\Rrightarrow y(56)=70\)
\(\\ \tt\Rrightarrow y=\dfrac{70}{56}\)
\(\\ \tt\Rrightarrow y=\dfrac{5}{4}\)
#2
\(\\ \tt\Rrightarrow (1-y)(3-y)(6-y)=120\)
\(\\ \tt\Rrightarrow -y(1+1)(3+1)(6+1)=120\)
\(\\ \tt\Rrightarrow -y(2)(4)(7)=120\)
\(\\ \tt\Rrightarrow 56y=-120\)
\(\\ \tt\Rrightarrow y=\dfrac{-120}{56}\)
\(\\ \tt\Rrightarrow y=\dfrac{-15}{7}\)
Answer:
i. y = 8, ii. y = -2Step-by-step explanation:
(1 - y)(3 - y)(6 - y) = -70We can see the divisors are 2 and 3 apart.
i.
Factorize -70 so that divisors are 2 and 3 apart:
- 70 = (- 2)*(- 5)*(- 7)The smallest one is 1 - y and -7:
1 - y = -7y = 1 + 7 y = 8ii
Factorize 120 so that divisors are 2 and 3 apart:
120 = 3*5*8The smallest one is 1 - y and 3:
1 - y = 3y = 1 - 3y = -2NO LINKS!! URGENT HELP PLEASE!!!
5. Find the domain and the range for each of the following graphs.

Answers
Answer:
Domain: x \(\geq\) -5
Range: y \(\geq\) -3
Step-by-step explanation:
The domain is all the possible inputs or x value. x will be greater than -5.
The range is all of the possible outputs or y value. y will be greater than -3
Answer:
Domain: [-5, ∞)
Range: [-3, ∞)
Step-by-step explanation:
The given graph shows a continuous curve with a closed circle at the left endpoint (-5, -3) and an arrow at the right endpoint.
A closed circle indicates the value is included in the interval.
An arrow shows that the function continues indefinitely in that direction.
DomainThe domain of a function is the set of all possible input values (x-values).
As the leftmost x-value of the curve is x = -5, and it continues indefinitely in the positive direction, the domain of the graphed function is:
Interval notation: [-5, ∞)Inequality notation: x ≥ -5Set builder notation: {x ∈ R | x ≥ -5 }RangeThe range of a function is the set of all possible output values (y-values).
From observation, it appears that the minimum y-value of the curve is y = -3. The curve continues indefinitely in the positive direction in quadrant I. Therefore, the range of the graphed function is:
Interval notation: [-3, ∞)Inequality notation: y ≥ -3Set builder notation: {y ∈ R | y ≥ -3 }Provide the reasons for the following proof.
The figure shows triangle W X Y with a segment X Z drawn from vertex X to point Z on side W Y.
Given: Segment W X is congruent to Segment X Y and segment X Z bisects angle W X Y
Prove: triangle W X Z is congruent to triangle Y X Z
Statements Reasons
1.Segment W X is congruent to Segment X Y and segment X Z bisects angle W X Y 1. Given.
2. angle W X Z is congruent to angle Y X Z 2. Definition of an angle bisector.
3. Segment X Z is congruent to segment X Z. 3. _____________
4. triangle W X Z is congruent to triangle Y X Z 4. _____________
A. Reflexive Property of congruent to; SSS
B. Symmetric Property of congruent to; SSS
C. Reflexive Property of congruent to; SAS
D. Symmetric Property of congruent to; SAS
SOMEONE HELP! PLEASE!

Answers
The two column proof showing that ΔWXZ ≅ ΔYXZ is as shown below
From the given triangle, we see that;
Given: WX ≅ XY, XZ bisects WXY
Prove: ΔWXZ ≅ ΔYXZ
The two column proof for the above is as follows;
Statement 1; WX ≅ XY, XZ bisects 2
Reason 1; Given
Statement 2: ∠WXZ ≅ YXZ
Reason 2; Angle bisector
Statement 3; XZ ≅ XZ
Reason 3: Reflexive property of congruence
Statement 4: ΔWXZ ≅ ΔYXZ
Reason 4: SAS Congruence Postulate
Read more about two column proof at; https://brainly.com/question/1788884
#SPJ1
2,239 ÷ 7
Division compatible numbers
Answers
Answer:the answer is 319.857 and round to 320
Step-by-step explanation:
Multiply.
(2x+6)²
NEED ANSWER ASAPP
Answers
Answer:
4x² + 24x + 36
Step-by-step explanation:
(2x + 6)² = (2x + 6)(2x + 6) = 4x² + 12x + 12x + 36 = 4x² + 24x + 36
The weights X of an animal are distributed according to the
probability distribution shown.
What is the probability that the animal's weight will be less than
151 pounds?
O 0.25
O 0.50
O 0.60
O 0.75
Answers
The probability that the animal's weight will be less than 151 pounds is 0.50.
The correct option is B.
What is the probability that the animal's weight will be less than 151 pounds?Since the given probability distribution ranges from 148 to 152, and we need to find the probability that the animal's weight will be less than 151 pounds, we can add the probabilities corresponding to the weights less than 151.
From the distribution, we see that the probability of the animal's weight being less than 151 pounds is 0.2 + 0.3 = 0.5.
Therefore, the answer is O 0.50.
Learn more about probability at: https://brainly.com/question/251701
#SPJ1
A farmer is building a fence to enclose a rectangular area against an existing wall, shown in the figure below. Three of the sides will require fencing and the fourth wall already exists. If the farmer has 176 feet of fencing,
what is the largest area the farmer can enclose?
Answers
Answer: 46 ft by 92 ft
Step-by-step explanation:
The largest area is enclosed when half the fence is used parallel to the wall and the other half is used for the two ends of the fenced area perpendicular to the wall. Half the fence is 184 ft/2 = 92 ft. Half that is used for each end of the enclosure.
In which part of the graph is the height of the water increasing?

Answers
Answer:
1
Step-by-step explanation:
1 is increasing
2 is staying constant
3 is decreasing
4 is staying constant again
5 is also decreasing
Slope 3/5 yintercept2 write an equation slope-intercept form
Answers
The equation of the line in slope-intercept form is y = (3/5)x + 2. This form allows us to easily identify the slope and y-intercept of the line and to graph it on a coordinate plane.
To write the equation of a line in slope-intercept form, we use the formula:y = mx + b
where:
- y represents the dependent variable (the vertical axis)
- x represents the independent variable (the horizontal axis)
- m represents the slope of the line
- b represents the y-intercept, the point where the line intersects the y-axis.
In this case, we are given the slope as 3/5 and the y-intercept as 2. Plugging these values into the formula, we get:
y = (3/5)x + 2
This equation represents a line with a slope of 3/5, indicating that for every 5 units we move horizontally (along the x-axis), the line moves 3 units vertically (along the y-axis). The y-intercept of 2 tells us that the line intersects the y-axis at the point (0, 2).
for more search question coordinate
https://brainly.com/question/30197038
#SPJ8
What is the solution for the following system of equations?
y=-3x+8 and x=2 Solution:y =______
Choose the correct description for this system:
This system is _____________________________(independent or dependent) and
__________________________ (consistent or inconsistent). This system has solutions_____________
(no solutions, infinite solutions or one solution).
Answers
Answer:
y=2
Step-by-step explanation:
Multiply -3(2) which gives -6, -6+8=2
Thus, y=2
If anyone can help me to solve this!!

Answers
Answer:
\(y = \dfrac{1}{2}x -5\)
Step-by-step explanation:
The slope intercept form of a linear equation is
y = mx + b
where m = slope and b = y-intercept
Since these are given, simply plug in to get
\(y = \dfrac{1}{2}x -5\)
how might the area of a room affect the way the room is used?
Answers
Answer:
The more area a room has the more things you can put in it
Step-by-step explanation:
4 ft
6 ft
T4ft-
8 ft
1. List the shapes that make up the front of the house.

Answers
The answer on shape of house is , (1) A rectangle for the main structure of the house. (2) A triangle for the roof. (3) A rectangle for the front porch. (4) Two trapezoids for the roof of the front porch. (5) A rectangular door.
What is Trapezoid?A trapezoid is a four-sided geometric shape with two parallel sides, called the bases, that are of different lengths, and two non-parallel sides that connect the bases. The non-parallel sides are also called legs, and they may or may not be equal in length.
Trapezoids are often encountered in geometry and in real-life situations, such as in construction and architecture. They can be classified as either right trapezoids or oblique trapezoids depending on whether one of the angles formed by the bases and a leg is a right angle or not.
Based on the image provided, the shapes that make up the front of the house are:
A rectangle for the main structure of the house. A triangle for the roof.A rectangle for the front porch.Two trapezoids for the roof of the front porch.A rectangular door.To know more about Oblique trapezoids visit:
https://brainly.com/question/301903
#SPJ1
Altitude/leg Theorem. Solve for x. Please help me it would be very appreciated

Answers
Using Altitude/leg Theorem. The solution for x are:
No.3: x = 12 units
No. 4: x = 8√3 units
How to solve for the altitude, x of the triangles?The altitude theorem states that the altitude of the right triangle can be found by taking the square root of the product of the two segments of the hypotenuse that are created when the altitude is drawn.
In mathematical notation, if we have a right triangle with legs a and b, and hypotenuse c, and if h is the length of the altitude drawn from the right angle to the hypotenuse, then we have:
h² = ab
or
h = √(ab)
No. 3
Using the altitude theorem:
x = √(16*9)
x = 12 units
The Leg Rule states that the length of each leg of a right triangle can be found by taking the square root of the product of the hypotenuse and the adjacent segment on that leg.
In mathematical notation, if we have a right triangle with legs a and b, and hypotenuse c, then we have:
a² = bc or a = √(bc) and
b² = ac or b = √(ac)
No. 4
hypotenuse = 12 + 4 = 16
x = √(16 * 12)
x = 8√3 units
Learn more about altitude theorem on:
https://brainly.com/question/14357999
#SPJ1
16 – (3 – 4y) = 2(y + 2)
Answers
Answer:
\(y = -4\frac{1}{2}\)
Step-by-step explanation:
\(16-(3-4y) = 2(y+2)\)
Distribute.
\(16 - 3 + 4y = 2y + 4\)
Combine like terms.
\(13 + 4y = 2y + 4\)
Subtract \(2y\) from both sides.
\(13 + 2y = 4\)
Subtract 13 from both sides.
\(2y = -9\)
Divide both sides by 2.
\(y = -4\frac{1}{2}\)
I hope this helps!
Solve the polynomial equation = 3
Answers
Answer:
lol the is no equation there to solve
SOMEBODY HELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIEST
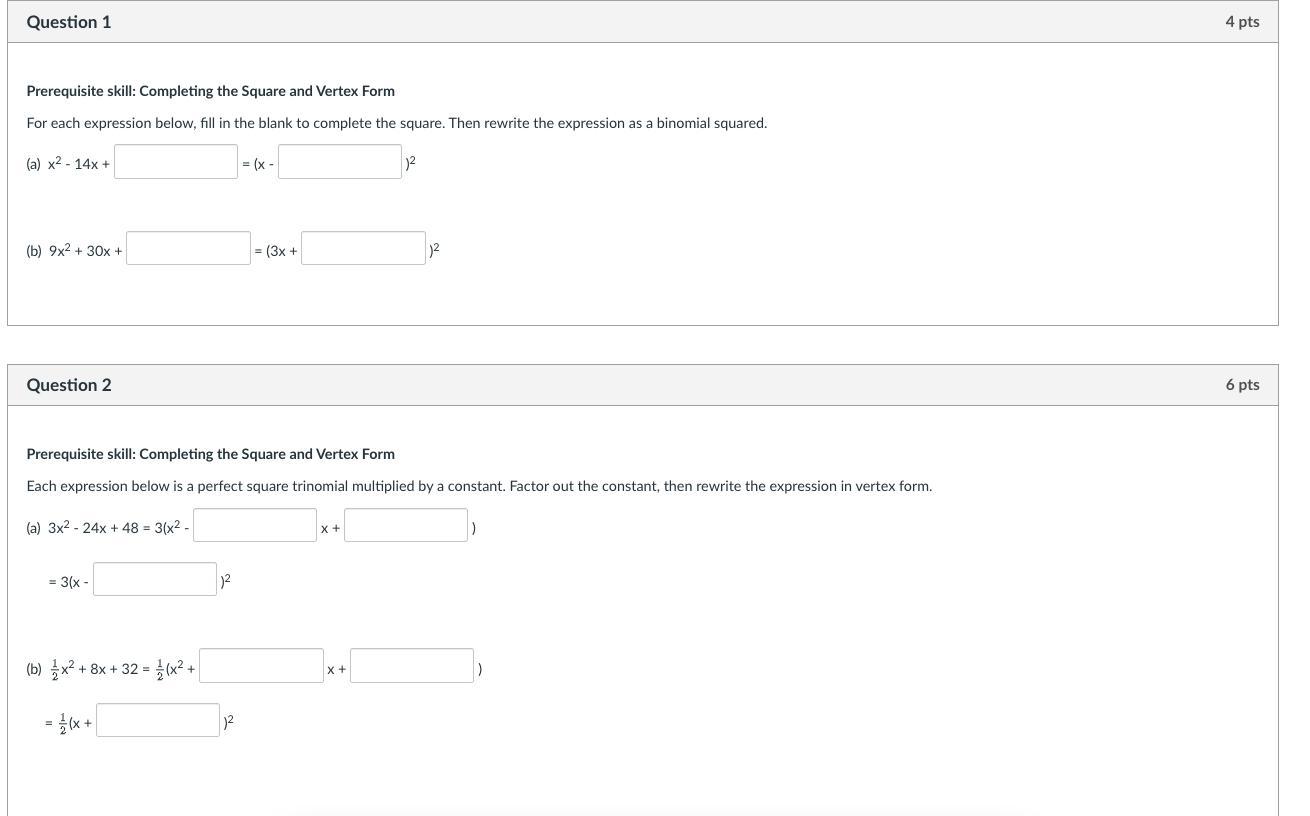
Answers
Answer:
\(\textsf{1.(a)} \quad x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
\(\textsf{1.(b)} \quad 9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\begin{aligned}\textsf{2.(a)}\quad3x^2-24x+48&=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\\&=3\left(x-\boxed{4}\right)^2\end{aligned}\)
\(\begin{aligned}\textsf{2.(b)}\quad \dfrac{1}{2}x^2+8x+32&=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\\&=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\end{aligned}\)
Step-by-step explanation:
Question 1(a) When completing the square for a quadratic equation in the form ax² + bx + c where the leading coefficient is one, we need to add the square of half the coefficient of the x-term:
\(x^2-14x+\left(\dfrac{-14}{2}\right)^2\)
\(x^2-14x+\left(-7\right)^2\)
\(x^2-14x+49\)
We have now created a perfect square trinomial in the form a² - 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Therefore:
\(a^2=x^2 \implies a=1\)
\(b^2=49=7^2\implies b = 7\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
(b) When completing the square for a quadratic equation where the leading coefficient is not one, we need to add the square of the coefficient of the x-term once it is halved and divided by the leading coefficient, and then multiply it by the leading coefficient:
\(9x^2 + 30x +9\left(\dfrac{30}{2 \cdot 9}\right)^2\)
\(9x^2 + 30x +9\left(\dfrac{5}{3}\right)^2\)
\(9x^2 + 30x +9 \cdot \dfrac{25}{9}\)
\(9x^2 + 30x +25\)
We have now created a perfect square trinomial in the form a² + 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 +2ab + b^2 = (a +b)^2}\)
Therefore:
\(a^2=9x^2 = (3x)^2 \implies a = 3x\)
\(b^2=25 = 5^2 \implies b = 5\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\hrulefill\)
Question 2(a) Factor out the leading coefficient 3 from the given expression:
\(3x^2-24x+48=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\)
We have now created a perfect square trinomial in the form a² - 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=3\left(x-\boxed{4}\right)^2\)
(a) Factor out the leading coefficient 1/2 from the given expression:
\(\dfrac{1}{2}x^2+8x+32=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\)
We have now created a perfect square trinomial in the form a² + 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2+2ab + b^2 = (a +b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\)
Step-by-step explanation:
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
For the truncated cuboid of height 3 m, top 5 m, base 8 m and side length of 1.5 m. Find the volume
Answers
Therefore, the volume of the truncated cuboid is approximately 68 + 4*√(30) cubic meters.
What is volume?Volume is a measure of the amount of space occupied by a three-dimensional object. It is the amount of three-dimensional space enclosed by the boundaries of an object. Volume is typically measured in cubic units, such as cubic meters (m³) or cubic centimeters (cm³).
Here,
The truncated cuboid is a solid figure that is obtained by cutting off the top of a rectangular prism (cuboid) with a plane that is parallel to the base. The formula for the volume of a truncated cuboid is:
V = h/3 * (A + √(A*B) + B)
where V is the volume, h is the height of the truncated portion, A is the area of the top face, and B is the area of the base face.
In this case, the height of the truncated portion is 3 m, the top face has an area of 5 m x 8 m = 40 m², and the base face has an area of 8 m x 1.5 m = 12 m². Therefore:
A + B = 40 + 12 = 52 m²
√(AB) = √(4012) = √(480) = 4*√(30)
Substituting these values into the formula, we get:
V = 3/3 * (52 + 4√(30) + 12)
V = 68 + 4√(30)
To know more about volume,
https://brainly.com/question/28338582
#SPJ1