The mapping diagram shows a functional relationship.
Complete the statement.
f(3) is
Domain
Range
0
3
Tomos
-1
9
9

Answers
Answer:
its -1
Step-by-step explanation:
cuz
Answer: it’s -1
Step-by-step explanation:
I just did the test
Related Questions
what is 9×4−(2×1/2)
(1/2 Is a fraction btw)
Answers
Answer:
35
Step-by-step explanation:
I used Symbolab here's the screenshot

The formula V = s3 give the volume V of a cube with side length s.
The volume of a cube that has a side length of 8 inches is inches cubed.

Answers
Answer:
512 inches cubed
Step-by-step explanation:
8^3 is equal to 512
Answer:
512 inches
Step-by-step explanation:
8^3 = 8*8*8 = 64*8 = 512 inches
Which of the following rational functions is graphed below?
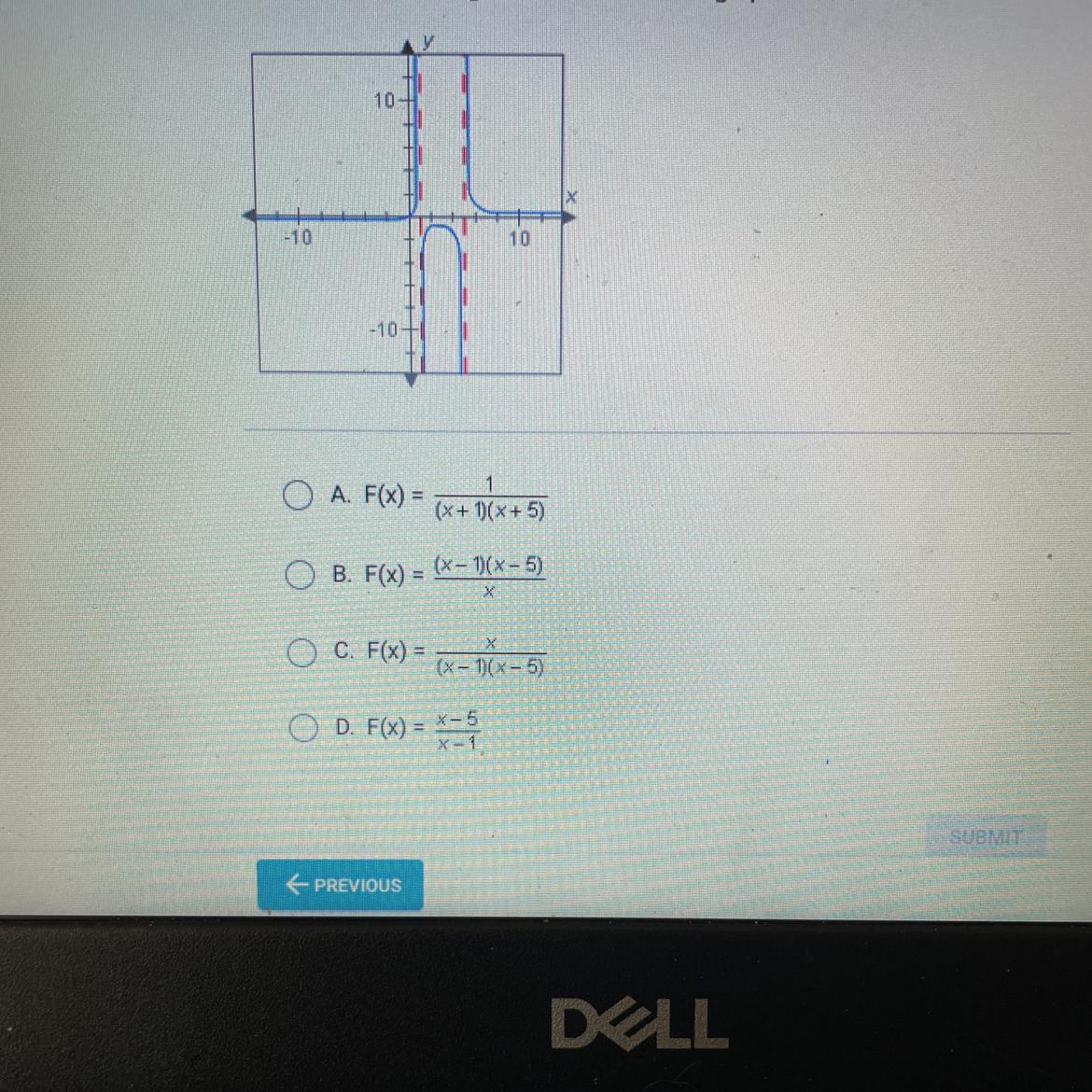
Answers
The rational function for this problem is defined as follows:
A. F(x) = 1/[(x + 1)(x + 5)]
How to define the rational function?The vertical asymptotes are the values of x which are outside the domain, which in a fraction are the zeroes of the denominator, hence they are given as follows:
x = 1 and x = 5.
Hence the denominator is given as follows:
(x - 1)(x - 5).
The function has no intercepts, hence the numerator is a constant.
Thus the function is given as follows:
A. F(x) = 1/[(x + 1)(x + 5)]
More can be learned about rational functions at brainly.com/question/1851758
#SPJ1
a uniform continuous distribution has a maximum of 14 and a minimum of 2. samples of size 36 are drawn from the distribution. what is the variance of the sample means?
Answers
The variance of the sample means that is found in the sample distribution that we have here is 0.3333
What is variance?This is the measure of dispersion that is used to show the spread of the data that is contained in a data set
The formula that we are to use here is given as
b² - a² / b - a
we have to put the values in this question
(14 - 2)² / 14 - 2
= 144 / 12
= 12
From here we would have to solve for the variance.
The variance = 12 / 35
= 0.3333
Hence the variance that we have in the question is equal to 0.3333
Read more on variance here: https://brainly.com/question/25639778
#SPJ1
Please help me with my maths homework all answer

Answers
Answer:
16: 24ab, a negative times a negative always makes a positive by the way
17: 6x^4
18: 15, 15-8=7, then 7x3=21
19: -2x+8
20: 8a
21: y x y x y
22: 2a+3b
23: 6a^4
24: x times x times x times x
25: 49y^2
the common endpoint of two rays that form an angle
Answers
Answer:
The vertex.
Step-by-step explanation:
I really need help in this plz help if ur here

Answers
Answer:
watch a video or use a hint.
Step-by-step explanation:
it say it.
A customer at a store paid $64 for 3 large candles and 4 small candles. At the same store, a second customer paid $4 more than the first customer for 1 large candle and 8 small candles. The price of each large candle is the same, and the price of each small candle is the same.
Which system of equations can be used to find the price in dollars of each large candle, x , and each small candle, y ?
Answers
Step-by-step explanation:
Plug in x where you see large candle and y for small candle
64= 3x + 4y
64+4= x+ 8y
Fill in the blank. The ________ is the probability of getting a test statistic at least as extreme as the one representing the sample data, assuming that the null hypothesis is true.
A. p-value
B. Critical value
C. Level of significance
D. Sample proportion
Answers
The p-value is the probability of getting a test statistic at least as extreme as the one representing the sample data, assuming that the null hypothesis is true.
The p-value is the probability of obtaining a test statistic that is as extreme as, or more extreme than, the one observed from the sample data, assuming that the null hypothesis is true. It is a measure of the evidence against the null hypothesis provided by the data. The p-value is used in hypothesis testing to make decisions about the null hypothesis. If the p-value is less than the predetermined level of significance (alpha), typically 0.05, it suggests that the observed data is unlikely to occur by chance alone under the null hypothesis. This leads to rejecting the null hypothesis in favor of the alternative hypothesis. On the other hand, if the p-value is greater than the significance level, there is insufficient evidence to reject the null hypothesis.For more questions on probability :
https://brainly.com/question/13786078
#SPJ8
Ms.Salgado needs to have her car repaired but does not want to spend more than $375 for the repairs. The mechanic says that the part needed for the repair will cost $100 and the labor will cost an additional $40 per hour. Which inequality below represents the greatest number of hours mechanic can work without exceeding ms. Salgado’s budget?
Answers
Answer:
6 hours without exceeding
Step-by-step explanation:
7 hours goes over
100+40x7=380
6 hours is under
100+40x6=340
\((x - 7)(x - 5)\)
Answers
Step-by-step explanation:
X=7 or x=5
It might be two answer to this question
\(\huge\textsf{Hey there!}\)
\(\large\textsf{(x - 7) (x - 5)}\)
\(\large\text{DISTRIBUTE each of the numbers}\)
\(\large\textsf{x(x) + (-5)x + (-7(x) + (-7)(-5)}\)
\(\large\textsf{x(x) = \bf x}\bf ^2\)
\(\large\textsf{x(-5) = \bf -5x}\)
\(\large\textsf{-7(x) = \bf -7x}\)
\(\large\textsf{(-7)(-5) = \bf 35}\)
\(\mathsf{x^2 - 5x -7x + 35}\)
\(\large\text{COMBINE the LIKE TERMS}\)
\(\mathsf{x^2 -(5x - 7x) + 35}\)
\(\mathsf{-5x -7x = \bf -12x}\)
\(\mathsf{x^2 - 12x + 35}\)
\(\boxed{\huge\text{Answer: \bf x}^2 \huge\text{\bf - 12x + 35}}\huge\checkmark\)
\(\large\text{Good luck on your assignment and enjoy your day!}\)
~\(\frak{Amphitirite1040:)}\)
solve using the quadratic formula:
3x=2x^2-2
Answers
Answer:
\(x=2\\x=-\frac{1}{2}\)
Step-by-step explanation:
1) Move terms to the left side.
\(3x=2x^{2} -2\\3x-(2x^{2}-2)=0\)
2) Distribute.
\(3x-(2x^{2} -2)=0\\3x-2x^{2} +2=0\)
3) Rearrange terms.
\(3x-2x^{2} +2=0\\-2x^{2} +3x+2=0\)
4) Common factor.
\(-2x^{2} +3x+2=0\\-(2x^{2} -3x-2)=0\)
5) Divide both sides of the equation by the same term.
\(-(2x^{2} -3x-2)=0\\2x^{2} -3x-2=0\)
6) Use the quadratic formula.
\(x=\frac{-b+\sqrt{b^{2}-4ac } }{2a}\)
Once in standard form, identify a, b, and c from the original equation and plug them into the quadratic formula.
\(2x^{2} -3x-2=0\\a=2\\b=-3\\c=-2\)
\(x=\frac{-(-3)+\sqrt{(-3)^{2} -4*2(-2)} }{2*2}\)
7) Simplify.
Evaluate the exponent
\(x=\frac{3+\sqrt{(-3)^{2}-4*2(-2) } }{2*2}\)
\(x=\frac{3+\sqrt{9-4*2(-2)} }{2*2}\)
Multiply the numbers
\(x=\frac{3+\sqrt{9-4*2(-2)} }{2*2}\)
\(x=\frac{3+\sqrt{9+16} }{2*2}\)
Add the numbers
\(x=\frac{3+\sqrt{9+16} }{2*2}\)
\(x=\frac{3+\sqrt{25} }{2*2}\)
Evaluate the square root
\(x=\frac{3+\sqrt{25} }{2*2} \\x=\frac{3+5}{2*2}\)
Multiply the numbers
\(x=\frac{3+5}{2*2}\)
\(x=\frac{3+5}{4}\)
8) Seperate the equations.
To solve for the unknown variable, separate into two equations: one with a plus and the other with a minus.
\(x=\frac{3+5}{4}\)
\(x=\frac{3-5}{4}\)
9) Solve.
Rearrange and isolate the variable to find each solution.
\(x=2\\x=-\frac{1}{2}\)
123.7 cm= How many meters?
Answers
123.7 cm = 1.237 meters
hope it helps.
Outside temperature over a day can be modelled as a sinusoidal function. Suppose you know the high temperature for the day is 80 degrees and the low temperature of 40 degrees occurs at 3 AM. Assuming t is the number of hours since midnight, find an equation for the temperature, D, in terms of t.
Answers
If the outside temperature over a day can be modeled as a sinusoidal function and if the high temperature for the day is 80 degrees and the low temperature of 40 degrees occurs at 3 AM, assuming t is the number of hours since midnight, then an equation for the temperature, D, in terms of t is D = 20*sin(π/12(t-3)) + 60.
To find the equation, follow these steps:
The sinusoidal function can be represented as D = Asin(B(t-C)) + D where A = the amplitude, B = 2π/period, C = shift phase (horizontal shift) and D = vertical shift. The high temperature is 80 degrees and the low temperature is 40 degrees. Thus, the amplitude A = (80-40)/2 = 20. The temperature goes through one cycle from its highest point to its lowest point and back to its highest point, this cycle takes 24 hours, since the temperature is modeled over a day. Thus, the period, T, of the temperature is 24 hours. Thus, B = 2π/T = 2π/24 = π/12. The minimum temperature of 40 degrees occurs 3 hours after midnight. This is represented as C. Thus C = 3. Also, since the amplitude is 20, the maximum temperature is 20 degrees above 40 degrees= 20 + 40 = 60 degrees. Thus the vertical shift D is 60 degrees.Putting these values into the equation D = Asin(B(t-C)) + D we have D = 20sin(π/12(t-3)) + 60.Thus the equation for the temperature, D, in terms of t is D = 20sin(π/12(t-3)) + 60
Learn more about sinusoidal function:
brainly.com/question/3842330
#SPJ11
You toll a pair of dice. Find the following probabilities: Whats is the probability of rolling two 4's
Answers
Solution
A pair of dice rolled has a total of 36 possible outcomes
The number of two 4's = 1
An expression for the probability is
\(P(4,4)\text{ =}\frac{No\text{ of required events}}{No\text{ of total possible events}}\)No of required events = 1
Total no of possible events
Ms. Lawrence had $550 in her bank account. Thr next day she withdrew $120 to buy groceries. She deposited $200 two days later. Four days later she used her debit card to buy new shoes that cost $89. What was her bank account balance after these transactions?
Answers
Answer:
$541
Step-by-step explanation:
1). $550 - $120 = $430 left in her bank account.
2). $430 + $200 = $630 in her bank account.
3). $630 - $89 = $541 left in her bank account.
(Withdraw means removing some of your money out of your bank account, and deposit means putting money back in your bank account)
So, therefore, after all of those transactions, Ms. Lawrence's bank account has $541.
Hope this helps! <3
Can you help me please

Answers
Answer:
40 cm
Step-by-step explanation:
You do your area divided by your width I think (don't trust my answer)
Solve the recursion using all three methods in any order you choose. Clearly label each solution as recursion tree, substitution, or Master Theorem. (15pt: 5 for each method): T(n)=2T(n/2)+23n
Answers
The solution of the given recurrence relation `T(n) = 2T(n/2) + 23n` using all three methods are:`T(n) = Θ(nlog2n)`
Given recursive relation is `T(n) = 2T(n/2) + 23n`.
We have to solve the above recursion using all three methods in any order we choose and label each solution as recursion tree, substitution, or Master Theorem.
Now, let's solve the above recursion using all three methods one by one:
1. Recursion Tree method:
To solve the above relation using recursion tree method, we will create a tree and the value of each level will be the sum of the values of all nodes present in that level or the sum of all previous levels + current level.
The tree will look like:
Therefore, the answer of the given recurrence relation `T(n) = 2T(n/2) + 23n` using the recursion tree method is:
`T(n) = Θ(nlog2n)`
2. Substitution method:
To solve the above recurrence relation using the substitution method, we can assume a solution and prove it by the Mathematical induction method.
Let `T(n) = 2T(n/2) + 23n`
Then, `T(n/2) = 2T(n/4) + 23n/2`
Also, `T(n/4) = 2T(n/8) + 23n/4`
Therefore, `T(n) = 2(2T(n/4) + 23n/2) + 23n`Or, `T(n) = 2²T(n/2²) + 23n(1 + 2)`
In general, we have `T(n) = 2kT(n/2k) + 23n(1 + 2 + ... + 2k-1)`
When `n/2k = 1`Or, `k = log2n`
Therefore, `T(n) = 2log2nT(1) + 23n(1 + 2 + ... + 2log2n-1)`Or, `T(n) = 2log2nT(1) + 23n(2log2n - 1)`
As `T(1) = 1`
Therefore, `T(n) = Θ(nlog2n)`
Hence, the answer of the given recurrence relation `T(n) = 2T(n/2) + 23n` using the substitution method is:
`T(n) = Θ(nlog2n)`
3. Master Theorem method:
To solve the above recurrence relation using the Master theorem, we have to compare the function `nlogba` with the function `f(n)`.
Here, `a = 2`, `b = 2`, and `f(n) = 23n`.
As per the Master theorem:
`If f(n) = Θ(nlogba),
then T(n) = Θ(nlogba log2n)` `
= Θ(nlog2n)` if
`f(n) = 23n
= Θ(nlog2n)`
Therefore, the solution of the given recurrence relation `T(n) = 2T(n/2) + 23n` using the Master theorem is:
`T(n) = Θ(nlog2n)`
Hence, the solution of the given recurrence relation `T(n) = 2T(n/2) + 23n` using all three methods are:`T(n) = Θ(nlog2n)`
Learn more about Master Theorem from the given link :
https://brainly.com/question/31033429
#SPJ11
−7x + y = 15
6x − y = -12
Answers
Answer:
Here's your answer
Hope it helps!!
What type of correlation is shown by the graph?

Answers
Answer: Positive correlation
Step-by-step explanation:
As you go up and along the graph the values go up.
Both have to be increasing basically.
What is the value of xin the diagram below?
O A. 6
O B. 7
O C. 8
D. 9

Answers
Answer:
it should be 9 because 12÷6 givss you 2 so 54÷6 gives you 9
Find the missing number in this sequence
1,0,1,1,0,1,_,1,0,1,1,1,1,0...
Answers
Explanation- it start with a single 1 then two 1s then it would have to be three 1s then four 1s
Hope this helps :)
Cups are sold in packages of 8. Napkins are sold in packages of 12. What is the fewest number of packages of cups and the fewest number of packages of napkins that can be purchased so there will be the same number of cups as napkins? Hint**- What will you need to find GCF or LCM?
Answers
Answer:
24 packages
Step-by-step explanation:
Given
Represent Napkins with N and Cups with C
\(C = 8's\)
\(N = 12's\)
Required
Determine the smallest amount of N and C that will be equal
To do this, we simply calculate the LCM of N and C as follows:
List out the multiples of each..
\(C = 8,16,24,30....\)
\(N = 12,24,36,48...\)
The common multiple between both is 24.
Hence, 24 packages of N and C answers the question
Which of the system(s) below works best to solve by elimination? Why? System 1 : 3m+n=71 2m-n=30
System 2 : 4x+y=1 y=-2x+9
System 3 : 5x+4y=15 5x + 11y=22
Answers
Answer:
first option is easiest since it involves just adding both equations term by term.
3m+n=71
2m-n=30
Step-by-step explanation:
The first system looks like the easiest one, because the two equations are listed already in standard form, and the variable "n" appears as positive "n" in the first equation, and as its opposite "-n" in the second equation. Therefore the elimination method works directly by adding both equations term by term (thus cancelling out completely one of the variables in the resultant/combined equation.
If z is directly proportional to the product of x and y and if z is 10 when x is 4 and y is 5, then x, y, and z are related by the equation
Answers
The equation relating x, y, and z is:
z = 0.5 * x * y.
In the given problem, the relationship between x, y, and z can be expressed by the equation z = k * x * y, where k represents the constant of proportionality. By substituting the values of x = 4 and y = 5, when z is equal to 10, we can determine the value of the constant of proportionality, k, and further define the relationship between the variables.
To find the constant of proportionality, we substitute the known values of x = 4, y = 5, and z = 10 into the equation z = k * x * y. This gives us the equation 10 = k * 4 * 5. By simplifying the equation, we have 10 = 20k. To isolate k, we divide both sides of the equation by 20, resulting in k = 0.5. Therefore, the equation relating x, y, and z is z = 0.5 * x * y, meaning that z is directly proportional to the product of x and y with a constant of proportionality equal to 0.5.
To learn more about proportionality, click here: brainly.com/question/28194586
#SPJ11
suppose we are interested in studying the relationship between the shelf life of cheeses in a dairy factory and the thickness of the packaging material used for those cheeses. we would like to determine if there is a causal relationship between the thickness of the packaging material and the shelf life of the cheese; that is, does a change in the thickness of the packaging material cause a change in the shelf life of the cheese? select the study that would be best source of evidence for establishing the existence of a causal relationship.
Answers
To establish the existence of a causal relationship between the thickness of the packaging material and the shelf life of the cheese,
In a dairy factory, the best study that would be a reliable source of evidence is a randomized controlled trial (RCT).In an RCT, the participants are randomly assigned to two or more groups,
where one group receives the intervention (in this case, cheese packaged with thicker material) and the other group receives the standard treatment (cheese packaged with the usual material).
To ensure the reliability of the study, the RCT should be conducted in a double-blind manner, where neither the participants nor the researchers know which group is receiving the intervention. This will prevent any bias that may influence the results.
The participants should also be selected carefully to ensure that they represent the target population of the study. In this case, the participants should be cheese consumers or distributors who are interested in the shelf life of the cheese.
By comparing the shelf life of the cheese packaged with thicker material to that packaged with the usual material, the RCT can establish the existence of a causal relationship between the thickness of the packaging material and the shelf life of the cheese.
The results of the study can then be used to inform the dairy factory's packaging practices and improve the shelf life of their cheeses.
To know more about population click here
brainly.com/question/31544819
#SPJ11
compare the ratios 5:12 and 7:9
Answers
Answer: 5:12< 7:9
Step-by-step explanation: (5:12) x3= 15:36 < 21:36 (7:9)x3=21:36
Answer:
\(\frac{5}{12} < \frac{7}{9}\)
Step-by-step explanation:
\(5:12\) \(7:9\)
\(5*9\) \(7*12\) (using cross multiply)
\(45 < 84\)
Therefore your answer is \(\frac{5}{12} < \frac{7}{9}\)
Extra:
I hope this helped at all.
Note: (Please don't delete this answer moderators.)
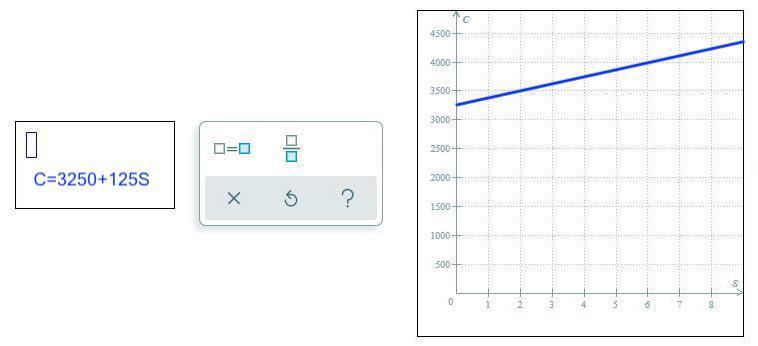
How do i solve this?

Answers
9514 1404 393
Answer:
see the attachment
Step-by-step explanation:
The cost when no sugar is transported is 3250, so that is the "y-intercept". (There is no "y". The vertical axis is labeled "c", so that is the c-intercept.)
The cost per ton is 125, so that is the slope or "rate of change". Each increase of 1 unit in the value of "s" will result in an increase of 125 in the value of "c". The grid lines for "c" are 500 apart, so 1 vertical grid space will correspond to 500/125 = 4 horizontal grid spaces.
The graph starts at the left side halfway between 3000 and 3500. It goes up 1 grid square for each 4 grid squares to the right.
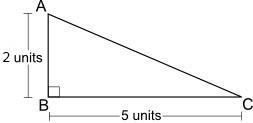
The area of the triangle above will equal one half of a rectangle that is 5 units long and __ units wide. (Input only whole numbers, such as 8.)
Answers
Answer:
2
Step-by-step explanation:
Find the diagram attached
The Base of the triangle will be equivalent to the the length of the rectangle
Since the base of the triangle is 5units, hence length of the rectangle is 5units
Similarly, the height of the triangle is corresponding to the width of the rectangle
Since the height of the triangle is 2 units, the rectangle will be 2 unts wide. Hence the required answer is 2units
there is a 60% chance that fund b will rise in price given that fund a rises in price. there is also a 30% chance that fund b will rise in price. what is the probability that a rises and b does not rise in price?
Answers
The probability that a rises and b does not rise in price is: 24%
We can use conditional probability to solve this problem.
Let A = "fund a rises in price" and B = "fund b rises in price".
From the information provided, we know that:
P(B|A) = 0.6 (the probability that fund b rises in price given that fund a rises in price)P(B) = 0.3 (the probability that fund b rises in price)Using the formula for conditional probability, we can find the probability that a occurs and b does not occur:
P(A and B') = P(A) * P(B'|A)We don't know the probability of a, but we can find it using the formula for conditional probability and Bayes' theorem:
P(A) = P(B|A) * P(A) / P(B)Substituting in the known probabilities:
P(A) = 0.6 * P(A) / 0.3Solving for P(A), we get:
P(A) = 0.6Now we can use this value to find P(A and B'):
P(A and B') = P(A) * P(B'|A)P(A and B') = 0.6 * (1 - P(B|A))P(A and B') = 0.6 * (1 - 0.6)P(A and B') = 0.24So, the probability that fund a rises in price and fund b does not rise in price is 0.24 or 24%.
To learn more about conditional probability, use the link:
brainly.com/question/30144287
#SPJ4