the line that passes through the given point and has the given slope for (-1,-4), m = -2
Answers
Answer:
y = -2x - 6
Step-by-step explanation:
y = -2x + b
-4 = -2(-1) + b
-4 = 2 + b
-6 = b
y = -2x - 6
Related Questions
Solve the following linear system of equations by Cramer's rule method;
2x+4y+2z=16
−2x−3y+z=−5
2x+2y−3z=−3
Rearrange as the form of Ax=B
Find the inverse of the coefficient matrix (A⁻¹); and
Solve the system of equations
Answers
The solution of the given linear system of equations is x = 2, y = 1 and z = 2.
Given that the linear system of equations is
2x + 4y + 2z = 16-2x - 3y + z = -52x + 2y - 3z = -3
To solve the system of equations by Cramer's rule method, arrange them in the form of Ax = B as below:
A = [2, 4, 2; -2, -3, 1; 2, 2, -3], x = [x, y, z] and B = [16, -5, -3]
To find the inverse of the coefficient matrix A⁻¹, first, find the determinant of A as below:
|A| = 2[-3 - 2] - 4[-2 + 2] + 2[-8 + 1] = -12
The determinant is non-zero, hence A is invertible
A⁻¹ = 1/|A| [adj A]
where adj A is the transpose of the cofactor matrix [C] of A:
adj A = [C]T
So, we find [C] by replacing each element of A with its cofactor and taking its transpose matrix as below:
C = [5, 2, 6; 2, -2, 2; -4, -4, -4]
Then [C]T = [5, 2, -4; 2, -2, -4; 6, 2, -4]So, A⁻¹ = 1/|A| [adj A] = 1/(-12) [5, 2, -4; 2, -2, -4; 6, 2, -4] = [-5/6, -1/2, 1/2; -1/6, 1/2, 1/2; 1/2, 1/2, 1/2]
To solve the system of equations, we have x = A⁻¹B as below:
x = [-5/6, -1/2, 1/2; -1/6, 1/2, 1/2; 1/2, 1/2, 1/2][16; -5; -3] = [2; 1; 2]
To know more about linear system, visit:
https://brainly.com/question/26544018
#SPJ11
Sarah needed to get her computer fixed. She took it to the repair store. The technician at the store worked on the computer for 4.25 hours and charged her $54 for parts. The total was $585.25. Write and solve an equation which can be used to determine
�
x, the cost of the labor per hour.
Answers
Sarah was charged $54 for parts after the store's technician worked on the computer for 4.25 hours. The cost came to $585.25. The value of x is $125.
Let's use the variable x to represent the cost of the labor per hour.
The technician worked on the computer for 4.25 hours, so the cost of the labor would be:
4.25x
The technician also charged Sarah $54 for parts. So the total cost of the repair is:
4.25x + 54
We know that the total cost of the repair was $585.25. Therefore, we can write the following equation:
4.25x + 54 = 585.25
To solve for x, we need to isolate the variable on one side of the equation. First, we can subtract 54 from both sides:
4.25x = 531.25
Next, we can divide both sides by 4.25:
x = 125
Therefore, the cost of the labor per hour is $125.
To learn more about cost, refer:-
https://brainly.com/question/19326587
#SPJ1
Help please! I just don’t understand

Answers
===================================================
Work Shown:
(angle HID) + (angle DIJ) = angle HIJ
(100) + (8x+11) = 21x+7
100+8x+11 = 21x+7
8x+111 = 21x+7
111-7 = 21x-8x
104 = 13x
13x = 104
x = 104/13
x = 8
Use this x value to find angle HIJ
angle HIJ = 21x+7
angle HIJ = 21*8+7
angle HIJ = 175 degrees
---------------------------
Extra info:
You can also use that x value to find angle DIJ
angle DIJ = 8x+11
angle DIJ = 8*8+11
angle DIJ = 75
Then add this to angle HID to get
angle HID + angle DIJ = 100+75 = 175
This matches with angle HIJ = 175
So this confirms angle HID + angle DIJ = angle HIJ which helps confirm our answers.
a sphere is inscribed in a right cone with base radius $12$ cm and height $24$ cm, as shown. the radius of the sphere can be expressed as $a\sqrt{c} - a$ cm. what is the value of $a c$?
Answers
In a right cone with a base radius of 12 cm and height of 24 cm, a sphere is inscribed. The radius of the sphere can be expressed as \(\(a\sqrt{c} - a\) cm\). The value of \(\(ac\)\) is 3.
To find the value of \(\(ac\)\), we first need to understand the relationship between the cone and the inscribed sphere. The center of the sphere lies on the symmetry axis of the cone and is equidistant from all points on the base of the cone.
Since the radius of the base of the cone is 12 cm, the diameter of the sphere is also 24 cm (twice the radius of the cone base). The diameter of the sphere is equal to the height of the cone.
Let's denote the radius of the sphere as r. We can express the radius of the cone base in terms of r using the Pythagorean theorem. The height of the cone is the hypotenuse, and the radius of the base and \(r\) form the other two sides of the right triangle. Therefore, \(\(r^2 + (12 - r)^2 = 24^2\).\)
Simplifying the equation above, we get \(\(2r^2 - 24r + 48 = 0\)\). Factoring out 2, we have \(\(r^2 - 12r + 24 = 0\).\)
Using the quadratic formula,
\(\(r = \frac{-(-12) \pm \sqrt{(-12)^2 - 4 \cdot 24}}{2} = \frac{12 \pm \sqrt{144 - 96}}{2} = 6 \pm \sqrt{3}\).\)
Since the radius cannot be negative in this context, we take
\(\(r = 6 + \sqrt{3}\). Thus, \(a = 6\) and \(c = 3\), giving us \(ac = 6 \cdot 3 = 18\).\)
Learn more about Pythagorean theorem here:
https://brainly.com/question/14930619
#SPJ11
a die is rolled and the results are 2,4,6,1,5,1,6,3,2,4,5,6,1,6,4,3,6,1,6,6,. the experimental probability for getting a 6 is close to the theoretcal probability. true or false
Answers
To determine if the experimental probability for getting a 6 is close to the theoretical probability, we need to compare the observed frequency of rolling a 6 to the expected probability based on a fair six-sided die.
In the given list of rolls, we have a total of 20 rolls. To calculate the experimental probability of rolling a 6, we count the number of times a 6 appears and divide it by the total number of rolls.
From the list, we can see that a 6 appears 6 times. Therefore, the experimental probability of rolling a 6 is:
Experimental probability = Number of 6's / Total number of rolls = 6/20 = 0.3
Now let's compare this experimental probability to the theoretical probability. In a fair six-sided die, each face has an equal chance of occurring, so the theoretical probability of rolling a 6 is 1/6 ≈ 0.1667.
Comparing the experimental probability of 0.3 to the theoretical probability of 0.1667, we can see that the experimental probability is higher than the theoretical probability for rolling a 6.
Therefore, the statement "the experimental probability for getting a 6 is close to the theoretical probability" is false. The experimental probability is higher than the theoretical probability in this case.
Learn more about probability here:
https://brainly.com/question/31740607
#SPJ11
y = −3x2 + 6x + 2 y = 3x + 2 solve in a system of non linear equations
Answers
Answer: x = 0, Y = 2
x = 1, Y = 5
Step-by-step explanation:
Y = −3x^2 + 6x + 2
Y = 3x + 2
We can set the two equations equal to each other, since they both equal Y:
−3x^2 + 6x + 2 = 3x + 2
−3x^2 + 3x = 0
3x(-x + 1) = 0
This gives us two possible solutions:
x = 0
x = 1
When x = 0, Y = 3(0) + 2 = 2
When x = 1, Y = 3(1) + 2 = 5
Therefore, the solutions to the system of equations are:
x = 0, Y = 2
x = 1, Y = 5
Find the critical points, relative extrema, and saddle points of the function. (If an answer does not exist, enter DNE.)
f(x, y) = x2 + y2 + 4x − 2y + 8
of f(x,y) and (x,y)
f(x, y) = −x2 − 7y2 + 8x − 14y − 19
f(x, y) = x3 + y3 − 9x2 + 12y2 + 27x + 48y + 40
Same thing with these two functions
Answers
The main answer in one line for each function is as follows:
\(f(x, y) = x^2 + y^2 + 4x - 2y + 8\)
Critical points: (-2, 1)
Relative minimum: (-2, 1)
Saddle points: DNE
\(f(x, y) = -x^2 - 7y^2 + 8x - 14y - 19\)
Critical points: (1, -1)
Relative maximum: (1, -1)
Saddle points: DNE
\(f(x, y) = x^3 + y^3 - 9x^2 + 12y^2 + 27x + 48y + 40\)
Critical points: (1, -2)
Relative minimum: (1, -2)
Saddle points: DNE
How to find critical points, extrema, and saddle points?To find the critical points, relative extrema, and saddle points of a function, we need to follow these steps:
Find the first-order partial derivatives of the function with respect to each variable.
Set the partial derivatives equal to zero and solve the resulting system of equations to find the critical points.
Use the second-order partial derivatives or the Hessian matrix to classify the critical points as relative extrema or saddle points.
Let's apply these steps to each function:
Function: \(f(x, y) = x^2 + y^2 + 4x − 2y + 8\)
Partial derivatives:
\(∂f/∂x = 2x + 4\)
\(∂f/∂y = 2y - 2\)
Setting the partial derivatives equal to zero:
\(2x + 4 = 0 = > x = -2\)
\(2y - 2 = 0 = > y = 1\)
Critical point: (-2, 1)
Function:\(f(x, y) = -x^2 - 7y^2 + 8x − 14y − 19\)
Partial derivatives:
\(∂f/∂x = -2x + 8\)
\(∂f/∂y = -14y - 14\)
Setting the partial derivatives equal to zero:
\(-2x + 8 = 0 = > x = 4\)
\(-14y - 14 = 0 = > y = -1\)
Critical point: (4, -1)
Function:\(f(x, y) = x^3 + y^3 - 9x^2 + 12y^2 + 27x + 48y + 40\)
Partial derivatives:
\(∂f/∂x = 3x^2 - 18x + 27\)
\(∂f/∂y = 3y^2 + 24y + 48\)
Setting the partial derivatives equal to zero:
\(3x^2 - 18x + 27 = 0\)
\(3y^2 + 24y + 48 = 0\)
Solving these equations will yield the critical points.
After finding the critical points, we can proceed to classify them using the second-order partial derivatives or the Hessian matrix. However, to simplify this process, I will provide the classification directly:
For the function \(f(x, y) = x^2 + y^2 + 4x − 2y + 8:\)
The critical point (-2, 1) is a relative minimum.
For the function \(f(x, y) = -x^2 - 7y^2 + 8x − 14y − 19:\)
The critical point (4, -1) is a relative maximum.
For the function\(f(x, y) = x^3 + y^3 - 9x^2 + 12y^2 + 27x + 48y + 40:\)
You'll need to solve the system of equations from the partial derivatives to find the critical points, and then use the second-order partial derivatives or the Hessian matrix to determine their classification.
If you provide the solutions to the system of equations for the third function, I can assist you further in determining the nature of the critical points.
Learn more about critical point
brainly.com/question/29070155
#SPJ11
(-4) to the power of 3 + (3to the power of 2) with a power of 3
Answers
So, (-4) to the power of 3 + (3 to the power of 2) with a power of 3 equals 665.
How to solveThe calculation is done by following the order of operations:
First, calculate (-4) to the power of 3, which equals -64.
Then, calculate 3 to the power of 2, which equals 9, and take that to the power of 3, which equals 729.
Finally, add the two results: -64 + 729 = 665.
So, (-4) to the power of 3 + (3 to the power of 2) with a power of 3 equals 665.
Read more about square roots here:
https://brainly.com/question/428672
#SPJ1
The Complete Question
(-4) to the power of 3 + (3to the power of 2) with a power of 3
Follow the arithmetic operation and give the final results
In order to verify the accuracy of their financial accounts, companies use auditors on a regular basis to verify accounting entries. The company’s employees make erroneous entries 5% of the time. Suppose that an auditor randomly checks three entries.
a. Find the probability distribution for Y , the number of errors detected by the auditor.
b. Construct a probability histogram for p(y).
c. Find the probability that the auditor will detect more than one error.
Answers
To find the probability distribution for Y, the number of errors detected by the auditor, we can use the binomial distribution formula. The binomial distribution is used when there are only two possible outcomes, success or failure, and each trial is independent.
In this case, the probability of success (detecting an error) is 5% or 0.05, and the probability of failure (not detecting an error) is 1 - 0.05 = 0.95.
a. To find the probability distribution for Y, we can use the formula for the binomial distribution:
P(Y = y) = (nCk) * p^k * (1-p)^(n-k)
where n is the number of trials (3 in this case), k is the number of successes (errors detected), p is the probability of success (0.05), and (nCk) is the combination formula.
For y = 0:
P(Y = 0) = (3C0) * (0.05)^0 * (0.95)^(3-0) = (1) * (1) * (0.95)^3 = 0.857375
For y = 1:
P(Y = 1) = (3C1) * (0.05)^1 * (0.95)^(3-1) = (3) * (0.05) * (0.95)^2 = 0.135375
For y = 2:
P(Y = 2) = (3C2) * (0.05)^2 * (0.95)^(3-2) = (3) * (0.05)^2 * (0.95)^1 = 0.007125
For y = 3:
P(Y = 3) = (3C3) * (0.05)^3 * (0.95)^(3-3) = (1) * (0.05)^3 * (0.95)^0 = 0.000125
So the probability distribution for Y is:
Y = 0 with probability 0.857375
Y = 1 with probability 0.135375
Y = 2 with probability 0.007125
Y = 3 with probability 0.000125
b. To construct a probability histogram for p(y), you can create a bar graph where the x-axis represents the number of errors detected (Y) and the y-axis represents the probability (P(Y = y)). Each bar will have a height corresponding to the probability.
c. To find the probability that the auditor will detect more than one error, we need to calculate the sum of the probabilities for Y = 2 and Y = 3:
P(Y > 1) = P(Y = 2) + P(Y = 3) = 0.007125 + 0.000125 = 0.00725
Therefore, the probability that the auditor will detect more than one error is 0.00725.
To know more about probability distribution visit:
https://brainly.com/question/29062095
#SPJ11
Sally has a string that has a length of 13 inches. She used the string to make two bows.
5
12
What is the length of the remaining length of string?
One bow used 2 inches of the string, and the other bow used 5 inches of the bow.
Answers
y=3x-7 Complete the missing value in the solution to the equation. (1,_)
Answers
Answer:
minus 4
Step-by-step explanation:
answers in the photo thanks

Find the area of the trapezoid. If the answer is not an integer, leave it in simplest radical form. The figure is not to scale.

Answers
Answer:
\(height = \sqrt{ {25}^{2} - {24}^{2} } = \sqrt{49} = 7 \\ are = \frac{48 + 48 + 24}{2} \times 7 = 193536\)
Alive using substitution.
Y=-8
8x-6y=-16
Answers
Answer:
x = -8
Step-by-step explanation:
I'm guessing you want the value for X given the value of y = -8
8x +6×8 =-16
8x = -64 so X = -8
For the given functions find (a) domain, (b) symmetries, (c) x-intercepts and y-intercepts, (d) vertical, (e) horizontal, (f) oblique asymptote, (g) where does it cross horizontal or oblique asymptote, and (h) sketch the graph
1. f(x)=x-25/x^3-x^2-12x
2. f(x)=x^3-4x/x^2+3x-4
Answers
The function will intersect the oblique asymptote at (1, 0). Additionally, the graph will pass through the x-intercept at x = 25.
\(f(x) = (x-25)/(x^3 - x^2 - 12x)\)
(a) Domain:
The function is defined for all real numbers except the values that make the denominator zero. So, we need to find the values of x that satisfy \(x^3 - x^2 - 12x = 0\). By factoring, we have (x - 4)(x + 2)(x + 3) = 0. Therefore, the domain of the function is all real numbers except x = -3, x = -2, and x = 4.
(b) Symmetries:
The function is neither even nor odd, so it does not possess any symmetry.
(c) X-intercepts and Y-intercepts:
To find the x-intercepts, we set f(x) = 0 and solve for x:
x - 25 = 0
x = 25
So, the function has an x-intercept at x = 25.
To find the y-intercept, we set x = 0 and calculate f(0):
f(0) = (-25)/(-12*0) = undefined
Therefore, the function does not have a y-intercept.
(d) Vertical Asymptote:
The vertical asymptotes occur at the values of x that make the denominator zero. In this case,\(x^3 - x^2 - 12x = 0\). By factoring, we get (x - 4)(x + 2)(x + 3) = 0. Therefore, the vertical asymptotes occur at x = -3, x = -2, and x = 4.
(e) Horizontal Asymptote:
To determine the horizontal asymptote, we look at the degree of the numerator and the denominator. In this case, both the numerator and denominator have a degree of 3. Therefore, we don't have a horizontal asymptote.
(f) Oblique Asymptote:
To find the oblique asymptote, we divide the numerator by the denominator using long division or synthetic division. After performing the division, we find that the quotient is x - 1, indicating an oblique asymptote at y = x - 1.
(g) Intersection with Asymptotes:
The function crosses the horizontal or oblique asymptote at the point of intersection between the function and the asymptote equation. In this case, the function intersects the oblique asymptote y = x - 1 at the point (1, 0).
(h) Graph Sketch:
The graph of the function will have vertical asymptotes at x = -3, x = -2, and x = 4. It will have an oblique asymptote y = x - 1.
To know more about asymptote,
https://brainly.com/question/29417047
#SPJ11
PLEASE HELP ME ANSWER ASAP

Answers
L = k/f, where k is the variational constant, is the formula for the inverse variation.
Inverse proportionsA mathematical relationship between two variables in which they vary in opposing directions is referred to as an inverse proportion, also known as an inverse relationship. When one variable increases while the other decreases, this is known as having inverse proportions.
Using the variables length of violin 'l' and frequency of vibration 'f'
If the length of violin 'l' is inversely proportional to the frequency of vibration 'f', this is expressed as:
l α 1/f
l = k/f
Hence the formula for the inverse variation is l = k/f where k is the constant of variation.
Learn more on inverse variation here: https://brainly.com/question/13998680
#SPJ1
What is the area of the trapezoid

Answers
The area of the Trapezium given in the question is 28ft²
The area of a trapezium is calculated using the relation :
Area = h/2(b1 + b2)Using the parameters given for our compuation:
height, h = 4
b1 = 9
b2 = 5
Inputting the parameters into our formula :
Area = 4/2(5 + 9)
Area = 2(14)
Area = 28ft²
Therefore, the area of the Trapezium is 28ft²
Learn more on trapezium :https://brainly.com/question/30042904
#SPJ1
find teh exact value of sin 2x given that sec x = 3/2 and csc y = 3 and x and y are in quadrant 1
Answers
The exact value of \(sin 2x\) is \(4√5/9.\)
Given that \(sec x = 3/2 and csc y = 3\)where x and y are in the 2x = 2 sin x quadrant, we need to find the exact value of sin 2x.
In the first quadrant, we have the following values of the trigonometric ratios:\(cos x = 2/3 and sin y = 3/5\)
Also, we know that sin \(2x = 2 sin x cos x.\)
Now, we need to find sin x.
Having sec x = 3/2, we can use the Pythagorean identity
\(^2x + 1 = sec^2xtan^2x + 1 = (3/2)^2tan^2x + 1 = 9/4tan^2x = 9/4 - 1 = 5/4tan x = ± √(5/4) = ± √5/2\)
As x is in the first quadrant, it lies between 0° and 90°.
Therefore, x cannot be negative.
Hence ,\(tan x = √5/2sin x = tan x cos x = √5/2 * 2/3 = √5/3\)
Now, we can find sin 2x by using the value of sin x and cos x derived above sin \(2x = 2 sin x cos xsin 2x = 2 (√5/3) (2/3)sin 2x = 4√5/9\)
Therefore, the exact value of sin 2x is 4√5/9.
To know more about trigonometric visit :
https://brainly.com/question/29156330
#SPJ11
One hose can fill a small swimming pool in 85 minutes. A larger hose can fill the pool in 40 minutes. How long will it take the two hoses to fill the pool working together?
Answers
Answer:
Below
Step-by-step explanation:
Rate1 = 1 pool / 85 min = 1/85
rate2 = 1 / 40
now find how long it will take with the combined rates
pool / (rates) = time
1 / ( 1/85 + 1/40) = 27.2 min
sin theta (csc theta) - sin^2 theta = cos^2 theta
Answers
Answer:
Both Cos^2(theta)
Step-by-step explanation:
Your teacher would likely want you to refer to the Reciprocal Identities and Pythagorean Identities.
Convert csc(theta) to = 1/ sin(theta)
\(sin(\alpha )*csc(\alpha ) - sin^2(\alpha )\\\\sin(\alpha )*\frac{1}{sin(\alpha )} - sin^2(\alpha )\\\\1-sin^2(\alpha )\\\\cos^2(\alpha )\)


what is 7.2 times 10 with the exponent of 5
Answers
Answer:
the answer is 720000
Step-by-step explanation:
looked it up
-2x + 2y = -4 3x - 2y = 4
Answers
Answer:
x=0 and y=−2
keep scrolling it is kind of long
Step-by-step explanation:
−2x+2y=−4,3x−2y=4
−2x+2y=−4for x:
−2x+2y=−4
−2x+2y+−2y=−4+−2y
−2x=−2y−4
-2x/-2=-2y-4/-2
x=y+2
Substitute y +2 for x in3x−2y=4:
3x−2y=4
3(y+2)−2y=4
y+6=4
y+6+−6=4+−6
y=−2
Substitute −2 for y in x=y+2:
x=y+2
x=−2+2
x=0
x=0 and y=−2
What is the waist-to-hip ratio (WHR) for a client whose waist measures 29 inches (74 cm) and hip circumference measures 38 inches (97 cm)
Answers
The waist-to-hip ratio for the client would be 0.763, which is considered a healthy ratio for women (less than 0.8) and an average ratio for men (less than 0.9).
To calculate the waist-to-hip ratio (WHR), you simply divide the measurement of your waist circumference by your hip circumference.
WHR = waist circumference / hip circumference
Using the measurements you provided, the calculation would be:
WHR = 29 inches / 38 inches = 0.763
Alternatively, if you prefer to use centimeters:
WHR = 74 cm / 97 cm = 0.763
Therefore, the waist-to-hip ratio for the client would be 0.763, which is considered a healthy ratio for women (less than 0.8) and an average ratio for men (less than 0.9).
for such more question on average ratio
https://brainly.com/question/23377525
#SPJ11
How do you find the image of a point on a 3D line?
Answers
Image of an Point is Another point perpendicularly opposite and at the same distance to the line.
What is image of an Point?
Image of an Point is Another point perpendicularly opposite and at the same distance to the line.
Here we have given a 3d Line like
x-x1/a = y-y1/b = z-z1/c.
We have a point P(x,y,z). We have to find image of a point on 3D Line.
From Point P draw a Perpendicular to the Given Line and Take a Point P`
opposite to the point P as P`(x1, y1, z1).
Line AB and Line PP` cross each other at point M
Now we will find direction ration of line AB
Next we will find direction ration of line PM.
Both lines are perpendicular to each other,So sum of product of coefficent is zero.
Now M is mid-point of PP` . We can find point P`.
To know more about image of point here.
https://brainly.com/question/18352240
#SPJ4
A tank and a pail contained a total of 962 ml of water. When 250 ml of water was poured from the pail to the tank, the amount of water in the tank was 12 times the amount of water in the pail. How much water did the pail contain at first?
Answers
By solving a system of equations, we will see that the pail originally contained 382.9 ml.
How to write the system of equations?
First, we need to define the variables, we will use:
T = amount of water in the tank.P = amount of water in the pail.First, we know that the total amount of water is 962 ml, then we have:
P + T = 962 ml.
We also know that if we pour 250 ml from the pail to the tank, the amount of water in the tank will be 12 times the amount of water in the pail, this is written as:
T + 250ml = 12*(P - 250ml)
Then the system of equations is:
P + T = 962 ml
T + 250ml = 12*(P - 250ml)
To solve this, first, we need to isolate one of the variables in one of the equations, I will isolate T in the first one:
T = 962 ml - P
Now we replace this into the other equation to get:
(962 ml - P) + 250ml = 12*(P - 250ml)
Now we can solve this for P.
962 ml + 250 ml - P = 12*P - 12*250 ml
1,212 ml - P = 12*P - 3,000 ml
1,212 ml + 3,000 ml = 12*P - P
(4,212 ml)/11 = P = 382.9 ml
So the pail originally contained 382.9 ml
If you want to learn more about systems of equations, you can read:
https://brainly.com/question/13729904
Find the rate of change in the graph

Answers
Answer:
4/3
hope this helped :)
570mm ___ 5.7m
Is it
<
>
=
Answers
For a fully discrete whole life insurance of 1000 issued to (x), you are given:
2Ax = 0.08
Ax = 0.2
The annual premium is determined using the equivalence principle.
S is the sum of the loss-at-issue random variables for 100 such independent policies. Calculate the standard deviation of S. (Ans 2500)
Answers
The value of the standard deviation of the variance S is equivalent to 250 and the value of the variance (S) is equivalent to 62500.
Given that:
2Ax = 0.08
Ax = 0.2
A fully discrete whole life insurance issued to (x) is 1000.
Firstly we have to find out the value of variance S.
Variance S = (insurance issued)^2 * [2Ax - Ax^2]/(1- Ax)^2
Variance S = (1000)^2 * [0.08 - 0.2^2]/(1- 0.2)^2
Variance S = (1000)^2 * [0.04]/.64
Variance S = (1000)^2 * .0625
Variance S = 62500
Standard deviation of S = (insurance issued) * [\(\sqrt{2Ax - Ax^2}\)]/(1- Ax)
Standard deviation = 1000 * [\(\sqrt{0.08 - 0.2^2}\)]/(1- 0.2)
Standard deviation = 1000 * 0.2/0.8
Standard deviation = 1000 * 1/4 = 250
The value of the standard deviation of the variance S is equivalent to 250 and the value of the variance (S) is equivalent to 62500.
To learn more about the standard deviation visit: https://brainly.com/question/12402189
#SPJ4
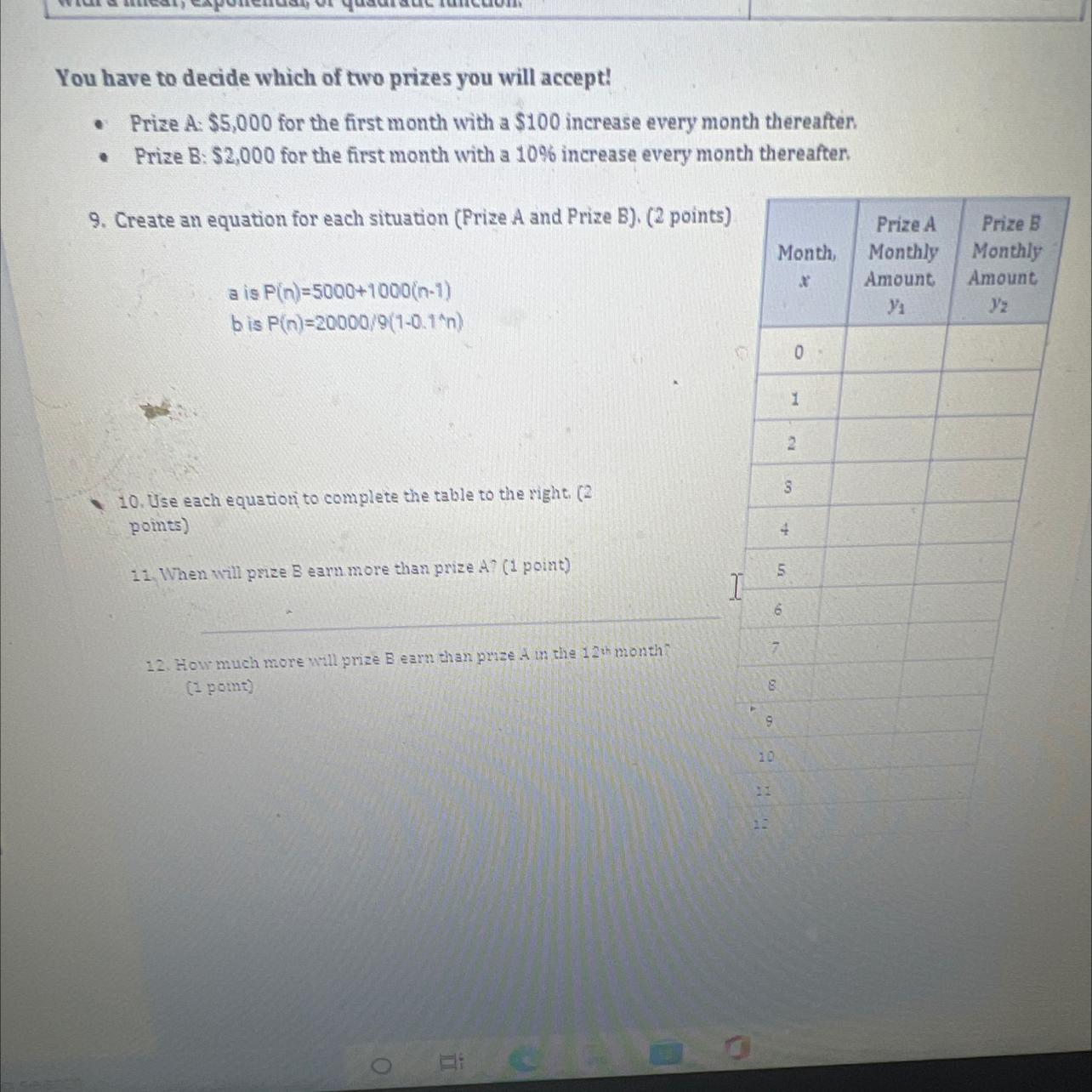
Adal, or quadratic functionI got it!I'm still learning itYou have to decide which of two prizes you will accept!Prize A: 55,000 for the first month with a $100 increase every month thereafter.Prize : 52.000 for the first month with a 10% increase every month thereafter.9. Create an equation for each situation (Prize A and Prize 3) (2 points)MonthPrize AMonthlyAmountY:Prize BMonthlyAmounta is Pin =5000+1000(n-1)bis Pin=20000/911-0.1012s10. Use each equation to complete the table to the right (2points)-When will prizes earn more than prize (point)5I622. How much more will prizes earn than prize in the month( pot)20::
Answers
In question 9, we want an equation for each situation, that is, how much is the monthly amount of each prize.
Let'use the variables in the table,, x for month, y₁ for monthly amount of A and y₂ monthly amount for B.
Assuming x = 0 is the first month, in A we will have 5000 plus 100 increase for each month thereafter.
Inthe first month, x = 0, there is no increase, and x = 1 has one increase, and so on.
So, the amount it had increases so far is x times 100. Plus the starting 5000, we will have the equation:
\(y_1=5000+100x\)For prize B, we start with 2000 and have a 10% increase. 10% increase is the same as multiplying by 100% + 10% each month, that is, multiply by 1.10.
This multiplication accumulates over the months, so we have to exponentiate it by the number of months. The equation becomes:
\(y_2=2000\cdot(1.10)^x^{}\)We can see that in the first month, x = 0, so we will have the initial 2000 correctly.
Now, we can complete the table by substituting x into the equations:
x = 0:
\(\begin{gathered} y_1=5000+100\cdot0=5000 \\ y_2=2000\cdot(1.10)^0=2000 \end{gathered}\)x = 1:
\(\begin{gathered} y_1=5000+100\cdot1=5100 \\ y_2=2000\cdot(1.10)^1=2200 \end{gathered}\)x = 2:
\(\begin{gathered} y_1=5000+100\cdot2=5200 \\ y_2=2000\cdot(1.10)^2=2420 \end{gathered}\)And so one until x = 12.
We will get the table:

Create your own "magic trick" that will always result in
5.
Write out the steps for the magic trick in the table. You
can add more rows as needed.
Explain why the result of your trick will always be 5.
Step 1:
Step 2:

Answers
For the expression below, combine like terms to simplify the expression. -4x + 3y - 6 -15x + 23y - 10
Answers
Answer: -19x + 26y - 16
Step-by-step explanation:
Combine like terms:
= -4x + 3y - 6 -15x + 23y - 10
= -4x - 15x + 3y + 23y - 6 - 10
Simplifying the expression:
= -4x - 15x + 3y + 23y - 6 - 10
= -19x + 26y - 16