The length of regular triangle is 5cm. A square has the same perimeter as of
triangle, then find the side length of square.
Answers
Perimeter of triangle = 3×side
Perimeter of square = 4× side
Side of triangle = 5cm
Perimeter of triangle = 3×5
=15 cm
Perimeter of triangle =Perimeter of square
15cm = 4× side of square
Side of square = 15÷4
=3.75 cm
Therefore ,Side of square is 3.75 cm .
Related Questions
Please help explain and answer

Answers
2.4
3. 9
4. 1/2
5. 2/-9
6. -1
7. 1
8. 7/4
When finding slope you want to subtract Y1 - Y2 and X1 -X2 to get your answer
The new figure that is produced in a transformation is called the

Answers
Let:
\(\begin{gathered} P=(x1,y1)=(-3,4) \\ P^{\prime}=(x2,y2)=(4,0) \end{gathered}\)\(\begin{gathered} x1+a=x2 \\ -3+a=4 \\ so\colon \\ a=4+3 \\ a=7 \\ ---- \\ y1+b=y2 \\ 4+b=0 \\ b=-4 \end{gathered}\)Therefore:
\((x,y)\to(x+7,y-4)\)Convert the decimal 0.75 to a percent.
Answers
Answer:
75%
Step-by-step explanation:
Type the correct answer in each box. Round your answers to the nearest dollar.
These are the cost and revenue functions for a line of 24-pound bags of dog food sold by a large distributor:
R(X) = -31. 72x2 + 2,030x
C(X) = -126. 96x +26,391
The maximum profit of $ 10277. 3.
can be made when the selling price of the dog food is set to $
3A
per bag
Reset
Next
Answers
The maximum profit of $10,277.3 can be made when the selling price of the dog food is set to $34 per bag.
To find the selling price that maximizes profit, we need to determine the price per bag that corresponds to the maximum profit. This can be done by finding the value of x (quantity) that maximizes the profit function.
The profit function can be calculated by subtracting the cost function from the revenue function:
Profit (P) = Revenue (R) - Cost (C)
P(x) = R(x) - C(x)
P(x) = (-31.72x^2 + 2,030x) - (-126.96x + 26,391)
P(x) = -31.72x^2 + 2,030x + 126.96x - 26,391
P(x) = -31.72x^2 + 2,157.96x - 26,391
To find the maximum profit, we need to find the vertex of the quadratic function. The x-coordinate of the vertex can be calculated using the formula:
x = -b / (2a)
In this case, a = -31.72 and b = 2,157.96. Let's calculate the x-coordinate:
x = -2,157.96 / (2 * -31.72)
x = -2,157.96 / -63.44
x ≈ 34
Now that we have the value of x, we can substitute it back into the profit function to find the maximum profit:
P(x) = -31.72(34)^2 + 2,157.96(34) - 26,391
P(x) ≈ $10,277.3
Therefore, the maximum profit of $10,277.3 can be made when the selling price of the dog food is set to $34 per bag.
Learn more about selling price here
https://brainly.com/question/31211894
#SPJ11
2Na + 2H2O —> 2NaOH+H2 how many grams of sodium would be needed to produce 1. 00kg of sodium hydroxide
Answers
Answer:
I am going to solve the question you have given without the use of the chemical equation.
The chemical formula of sodium chloride is NaOH
Molar mass: 40.0 g/mol
Molar mass of sodium: 23 g/mol
The mass of NaOH we have is 400kg which would be 400000g
Recall n = m/M (where n is the number of moles, m is the given mass, M is the molar mass):
Step-by-step explanation:

The base of a solid is a quadrant of a circle of radius a. Each cross section perpendicular to one edge of the base is a semicircle whose diameter lies in the base. Find the volume.
Answers
The volume of the given solid is πa³/4 cubic units.
Given that the base of a solid is a quadrant of a circle of radius a and each cross-section perpendicular to one edge of the base is a semicircle whose diameter lies in the base.
To find the volume of the solid, we'll integrate the area of the cross-section over the height of the solid.
Let us consider a cross-section with thickness dx at a distance x from the vertex of the quadrant, as shown in the figure below.
Here, the diameter of the semicircle forming the cross-section is 2(x + a).
Therefore, the radius of the semicircle is (x + a).
Area of the cross-section = Area of the semicircle= π[(x + a)²]/2
Volume of the solid = ∫Area dx from 0 to a= ∫π[(x + a)²]/2 dx from 0 to a= π/2 ∫(x² + 2ax + a²) dx from 0 to a= π/2 [(a³/3 + 2a²/2 + a³/2) - (0)] = πa³/4 cubic units
Therefore, the volume of the given solid is πa³/4 cubic units.
To know more about volume visit:
https://brainly.com/question/28058531
#SPJ11
A spaceship traveled 81 billion miles. In scientific notation that is _____ miles.
8.1 × 10 10
8.1 × 10 -9
8.1 × 10 9
8.1 × 10 -10
plz help it's being timed
Answers
Answer:
A (8.1 x 10^10)
Step-by-step explanation:
1. 1 billion is 1,000,000,000 or 10^9
2. 81 Billion should be 81 x 10^9, but the correct notation should always show a single digit number, so you need to also divide 81 per 10
3. Thus, the answer is 8.1 x 10^10
Answer:
8.1 × 10^10
:)
Ruth is knitting hats to sell at a local fair. The booth costs her $63 and the materials for each hat cost $10. She plans on selling them for $19. How many hats will Ruth have to make to break even, and how much will sales and costs be at that point?
Answers
Answer: Ruth have to make 7 hats to break even.
Step-by-step explanation:
Break even point is a point where Cost = Revenue.
Let x be the number of hats sold.
Given: Cost of booth = $63
Each hat cost = $10
Selling price for each cost = $19
As per given,
Total cost = Cost of booth+ (Cost of each hat)(Number of hats)
= 63+10x
Total selling price = 19x
For break even,
63+10x=19x
9x=63
x=7
Hence, Ruth have to make 7 hats to break even.
on a circle whose center is o, mark points p and a so that arc pa is a 46º arc. what does this tell you about poa ? extend segment po to meet the circle again at t. what is the size of pta ? this angle is inscribed in the circle, because all three points are on the circle. arc pa is considered intercepted or cut by pta.
Answers
On a circle with center O, points P and A are marked such that the arc PA is a 46º arc. This implies that angle POA is half the measure of the intercepted arc PA, which is 23º. When segment PO is extended to meet the circle again at point T, the size of angle PTA is also 23º
In a circle, the measure of an inscribed angle is half the measure of its intercepted arc. Since arc PA is a 46º arc, angle POA, which intercepts arc PA, will have half that measure, which is 23º.
When segment PO is extended to meet the circle again at point T, we can observe that angle PTA is an inscribed angle. As a result, angle PTA will also have the same measure as its intercepted arc PT. Since point P lies on arc PT, which has a measure of 46º, angle PTA will also measure 46º.
This relationship between the intercepted arc and the inscribed angle is a fundamental property of circles. It allows us to determine the measure of an inscribed angle if we know the measure of its intercepted arc, and vice versa. In this case, the measures of both angle POA and angle PTA are determined by the 46º arc PA.
Learn more about circle here:
https://brainly.com/question/12930236
#SPJ11
Determine the values of x and y such that the points (1,2,3), (4,7,1), and (x,y,2) are collinear (lie on a line). show complete steps.
Answers
The values of x and y that make the points (1,2,3), (4,7,1), and (x,y,2) collinear are x = 4 and y = 7. These values satisfy the condition that the vectors formed by the points are linearly dependent.
To determine the values of x and y such that the points (1,2,3), (4,7,1), and (x,y,2) are collinear, we need to check if the vectors formed by these points are linearly dependent. Two vectors are linearly dependent if and only if one is a scalar multiple of the other.
Let's consider the vectors formed by these points:
Vector v1 = (4-1, 7-2, 1-3) = (3, 5, -2)
Vector v2 = (x-1, y-2, 2-3) = (x-1, y-2, -1)
For these vectors to be linearly dependent, there must exist a scalar k such that v1 = k * v2.
Equating the corresponding components, we get the following system of equations:
3 = k * (x - 1)
5 = k * (y - 2)
-2 = -k
From the third equation, we find k = 1.
Substituting k = 1 into the first equation, we have:
3 = x - 1
x = 4
Substituting k = 1 into the second equation, we have:
5 = y - 2
y = 7
Therefore, the values of x and y that make the points (1,2,3), (4,7,1), and (x,y,2) collinear are x = 4 and y = 7.
To know more about collinear refer here:
https://brainly.com/question/5191807#
#SPJ11
2) Calculate the perimeter and area of the following shapes. Put the answer in pi notation
and rounded to the nearest tenth.
Height of Square- 5ft
Answers
The area of the square is 25ft² and the perimeter is 20ft.
How to illustrate the area?It's important to note that the area of a square is calculated as:
= Side ²
The perimeter is calculated as:
= 4 × Side
From the information given, the side is 5ft. The area will be:.
= 5 × 5
= 25ft²
The perimeter will be:
= 4 × Sode
= 4 × 5ft.
= 20 feet
Learn more about area on:
brainly.com/question/25292087
#SPJ1
What is the y-intercept of the line shown?


Answers
Answer:
C
Step-by-step explanation:
The Y-Intercept is when x = 0, or when it crosses the y-axis (vertical axis) You can see that the red line crosses the y-axis at 4, so that means the answer is just 4. (C)
Suppose that you're interested in the effect of class attendance on student performance: performance = Bo + Biattendance + B2ACT + B3GPA + u a. Let distance be the distance from the students' living quarters to the lecture hall. Assume distance and u are uncorrelated. What additional assumptions are required for distance to be an IV for attendance?
Answers
To determine if distance can be an instrumental variable (IV) for attendance in the model of given performance, we need to ensure that it satisfies the following assumptions: Relevance, Exogeneity and Exclusion restriction.
1. Relevance: Distance must be correlated with attendance, meaning that it has a significant effect on attendance. Intuitively, students living closer to the lecture hall may attend classes more frequently.
2. Exogeneity: Distance must not be directly correlated with the error term (u) in the performance equation, meaning that it should not have any direct effect on student performance apart from its impact on attendance. The assumption given already states that distance and u are uncorrelated, which fulfills this requirement.
3. Exclusion restriction: Distance should not have any direct effect on performance except through its influence on attendance. In other words, after controlling for attendance, ACT scores, and GPA, distance should not be a significant predictor of performance.
Additionally, we must assume that there are no other unobserved variables that could be driving the relationship between distance and performance. If these assumptions are met, we can use distance as an instrumental variable to identify the causal effect of attendance on performance.
Learn more about instrumental variable here:
https://brainly.com/question/23434609
#SPJ11
A new brewery is setting up its production facilities. It takes
6 weeks to brew a particular lager. If the brewery anticipates
serving 200 pints of this lager a day, how big of a vessel will the
brewe
Answers
It takes 6 weeks to brew a particular lager and the brewery anticipates serving 200 pints of this lager a day. To find: How big of a vessel will the brewery require? Solution: The brewery anticipates serving 200 pints of lager per day. It takes 6 weeks to brew a particular lager.
There are 7 days in a week. So, the total number of days required to brew the lager= 6 x 7= 42 days. It is given that the brewery anticipates serving 200 pints of lager per day. So, the total number of pints that the brewery will require to serve 200 pints per day for 42 days= 200 x 42= 8400 pints.1 gallon= 8 pints Therefore, 8400 pints= 8400/8 gallons= 1050 gallons. Hence, the brewery requires a vessel of 1050 gallons. Answer: 1050.
It was a definite and specific offer that could be accepted by anyone who met the requirements. It is an example of a unilateral offer since it was an open offer, anyone who agreed to the terms of the contract could have accepted it. Furthermore, it was a clear and unambiguous offer since it did not require any more clarification. Shawna and Beatrice, by virtue of their status as the offerees, had the option of accepting or rejecting the offer. The acceptance must meet the requirements of a valid contract. The acceptance must be communicated clearly and immediately. In addition, the acceptance must conform to the offer's terms. In Hyde v Wrench (1840), the court held that an acceptance must be unconditional and absolute and that if the acceptance is not in line with the terms of the offer, it is a counteroffer that terminates the original offer. Since Shawna and Beatrice had not yet responded to the offer, there was no acceptance of the contract. Therefore, there was no legal agreement between the parties as a contract must have both an offer and an acceptance in order to be considered valid.
To know more about Solution visit:
https://brainly.com/question/1616939
#SPJ11
What is the value of x?
Enter your answer in the box.
x =

Answers
Answer:
x = 98 degrees
Step-by-step explanation:
A heptagon has a total of 900 degrees for the interior angles. Add up all the angles and then subtract from 900 to find x.
146+122+142+140+110+142 = 802.
900-802 = 98
Answer:
x = 98
Step-by-step explanation:
This shape has 7 sides. Using the formula n - 2 we can get the number of triangles. n represents the number of sides.
n - 2 = 5
All triangles have 180 degrees, so multiply 180 by the number of triangles (5).
180 × 5 = 900
The total number of degrees in this shape is 900. Adding the other angle measures and then subtracting them from 900 gives us x.
146 + 122 + 142 + 140 + 110 + 142 = 802
900 - 802 = 98.
x = 98
2) Simplify |-5| + |6|. A) -30 B) -1 C) 1 D) 11
Answers
Answer:
D
Step-by-step explanation:
Answer: 11
Step-by-step explanation: The absolute value of -5 is 5. The absolute value of 6 is 6. So, 5+6=11
1. Laura earns $115 a month babysitting. If she saves all of the
money she earns in June and July and uses it to buy a bicycle
that cost $158, how much money will she have left?
A. $230,00
B. $43.00
C. $60.00
D. $72.00
A
B
OC
Answers
Answer:
Laura will have exactly $72.00 after purchasing the bicycle.
Step-by-step explanation:
We are given that Laura ends $115 per month of babysitting.
We also learn that she wants to save her money from June and July, which means she wants to save her money over a period of two months.
Therefore, she will earn $115 twice.
\(\displaystyle{\$115 \times 2 = \$230}\)
Then, she wants to purchase a bicycle that costs $158, so we need to subtract the cost of the bicycle from her total earnings.
\(\$230 - \$158 = \$72\)
Therefore, Laura will have exactly $72.00 remaining after her purchase.
please help me............................

Answers
The length of AI is 3.25 in
As we can see CD is 1.3 in and on GH is it 1.2 so we add that which gives us 2.5. But there is some space left in the middle. Looking at the right side there is the measurement of the space that is left which is 0.75. Which gives me 3.25 in
The length of IH is 4.5. I believe it is 4.5 in because IF is 9 in in total, but IH is only halfway, so 9 divided by 2 equals 4.5.
I hope this helps and that this is correct. My apologies for not being able to answer the last question and if there are wrong but I believe they are correct.
If
C(x) = 13000 + 400x − 3.6x2 + 0.004x3
is the cost function and
p(x) = 1600 − 9x
is the demand function, find the production level that will maximize profit. (Hint: If the profit is maximized, then the marginal revenue equals the marginal cost.)
units
Q 2
Find f.
f '''(x) = cos(x), f(0) = 4, f '(0) = 1, f ''(0) = 9
f(x) =
Q 3
A particle is moving with the given data. Find the position of the particle. a(t) = 2t + 3, s(0) = 9, v(0) = −4 s(t) =
Q 4
Find the most general antiderivative of the function. (Check your answer by differentiation. Use C for the constant of the antiderivative.)
f(x) = 6x5 − 7x4 − 6x2
F(x) =
Q 5
Factor the polynomial and use the factored form to find the zeros. (Enter your answers as a comma-separated list. Enter all answers including repetitions.)
P(x) = x3 + 3x2 − 9x − 27
x =
Answers
1. The production level that will maximize profit is 240 units.2. f(x) = sin(x) + x^3/3 + 4x + C where C is the constant of integration.
2. f(x) = sin(x) + x^3/3 + 4x + 1.
3. s(t) = 3t^2 + 2t + 9.
4. F(x) is the most general antiderivative of f(x).
5. The factorization of P(x) is (x - 3)(x + 3)^2.The zeros of P(x) are -3 and 3.
1. The production level that will maximize profit is 240 units. Given,
C(x) = 13000 + 400x - 3.6x^2 + 0.004x^3 = cost function
p(x) = 1600 - 9x = demand functionProfit = Total revenue - Total cost Let,
P(x) = TR(x) - TC(x)
where P(x) is profit function, TR(x) is total revenue function, and TC(x) is total cost function.
Now,
TR(x) = p(x) * x = (1600 - 9x) * x = 1600x - 9x^2and
TC(x) = C(x) = 13000 + 400x - 3.6x^2 + 0.004x^3
Let's differentiate both TC(x) and TR(x) to find the marginal cost and marginal revenue.
MC(x) = d(TC(x))/dx = 400 - 7.2x + 0.012x^2MR(x) = d(TR(x))/dx = 1600 - 18x
Now, if profit is maximized, then MR(x) = MC(x).1600 - 18x = 400 - 7.2x + 0.012x^21600 - 400 = 10.8x - 0.012x^2
1200 = x(10.8 - 0.012x^2)1200/10.8 = x - 0.00111x^3
111111.111 = 100000x - x^3
0 = x^3 - 100000x + 111111.111
From trial and error method, x = 240 satisfies the above equation.
Therefore, the production level that will maximize profit is 240 units.2. f(x) = sin(x) + x^3/3 + 4x + C where C is the constant of integration.
2. First, find f''(x) and f'''(x).
f''(x) = d/dx[f'(x)]
= d/dx[cos(x)]
= -sin(x)
f'''(x) = d/dx[f''(x)]
= d/dx[-sin(x)]
= -cos(x)Since f(0) = 4, f'(0) = 1, and f''(0) = 9,
f'(x) = f'(0) + integral of f''(x)dx
= 1 - cos(x) + C1
f(x) = f(0) + integral of f'(x)dx
= 4 + integral of (1 - cos(x))dx + C2
= 4 + x - sin(x) + C2
Now,
f(0) = 4, f'(0) = 1, f''(0) = 9
So, 4 + C2 = 4 => C2 = 0and
1 - cos(0) + C1 = 1 => C1 = 1
Therefore,
f(x) = sin(x) + x^3/3 + 4x + 1.
3. The position of the particle is given by the equation,
s(t) = s(0) + v(0)t + 1/2 a(t)t^2Given a(t) = 2t + 3, s(0) = 9, and v(0) = -4
s(t) = 9 - 4t + t^2 + 3t^2/2
s(t) = 3t^2 + 2t + 9.
4. The most general antiderivative of the function is given by,
F(x) = Integral of f(x)dxwhere f(x) = 6x^5 - 7x^4 - 6x^2Now,
F(x) = x^6 - 7x^5/5 - 2x^3 + C where C is the constant of integration.F'(x) = f(x)
= 6x^5 - 7x^4 - 6x^2
So, F(x) is the most general antiderivative of f(x).
5. First, find the factorization of P(x).
P(x) = x^3 + 3x^2 - 9x - 27
= x^2(x + 3) - 9(x + 3)
= (x^2 - 9)(x + 3)
= (x - 3)(x + 3)(x + 3)
Therefore, the factorization of P(x) is (x - 3)(x + 3)^2.The zeros of P(x) are -3 and 3.
To know more on equation visit
https://brainly.com/question/17145398
#SPJ11
Q1) The production level that will maximize profit is 111 units.
Q2) \(f(x) = sin(x) + x - cos(x) + x + 4\)
Q3) \(s(t) = (t³/3) + (3t²/2) - 4t + 9\)
Q4) \(F(x) = x⁶ - (7/5)x⁵ - 2x³ + C1\)
Q5) The zeros of the polynomial are: x = -3, 3
Q1) We are given the following equations:
\(C(x) = 13000 + 400x − 3.6x2 + 0.004x\)
\(3p(x) = 1600 − 9x\)
Given profit function:
\(π(x) = R(x) - C(x)\) where R(x) = p(x)*x is the revenue function
\(π(x) = x(1600-9x) - (13000 + 400x − 3.6x² + 0.004x³)\)
Taking the first derivative to maximize the profit
\(π'(x) = 1600 - 18x - (400 - 7.2x + 0.012x²)\)
\(π'(x) = 0\)
⇒ \(1600 - 18x = 400 - 7.2x + 0.012x²\)
Solving for x, we get: x = 111.11 ≈ 111 units (approx)
Hence, the production level that will maximize profit is 111 units.
Q2) We have been given: f '''(x) = cos(x), f(0) = 4, f '(0) = 1, f ''(0) = 9
Taking the antiderivative of f '''(x) with respect to x, we get:
\(f''(x) = sin(x) + C1\)
Differentiating f''(x) with respect to x, we get:
\(f'(x) = -cos(x) + C1x + C2\)
Differentiating f'(x) with respect to x, we get:
\(f(x) = sin(x) + C1x - cos(x) + C2x + C3\)
We know that f(0) = 4, f'(0) = 1 and f''(0) = 9
Putting the given values, we get: C1 = 1, C2 = 1, C3 = 4
Hence, \(f(x) = sin(x) + x - cos(x) + x + 4\)
Q3) We have been given: a(t) = 2t + 3, s(0) = 9, v(0) = −4
Using the initial conditions, we get: \(v(t) = ∫a(t)dt = t² + 3t + C1\)
Using the initial conditions, we get: C1 = -4
Hence, \(v(t) = t² + 3t - 4\)
Using the initial conditions, we get: \(s(t) = ∫v(t)dt = (t³/3) + (3t²/2) - 4t + C2\)
Using the initial conditions, we get: C2 = 9
Hence, s(t) = (t³/3) + (3t²/2) - 4t + 9
Q4) We need to find the antiderivative of \(f(x) = 6x⁵ - 7x⁴ - 6x²\)
Taking the antiderivative, we get: \(F(x) = (6/6)x⁶ - (7/5)x⁵ - (6/3)x³ + C1\)
Simplifying the above equation, we get: \(F(x) = x⁶ - (7/5)x⁵ - 2x³ + C1\)
Hence, \(F(x) = x⁶ - (7/5)x⁵ - 2x³ + C1\)
Q5) We have been given: \(P(x) = x³ + 3x² − 9x − 27\)
\(P(x) = (x-3)(x² + 6x + 9)\)
\(P(x) = (x-3)(x+3)²\)
Hence, the zeros of the polynomial are: x = -3, 3
Therefore, the answer is (-3, 3).
To know more about zeros, visit:
https://brainly.com/question/32640703
#SPJ11
just the answer and as many as can be help
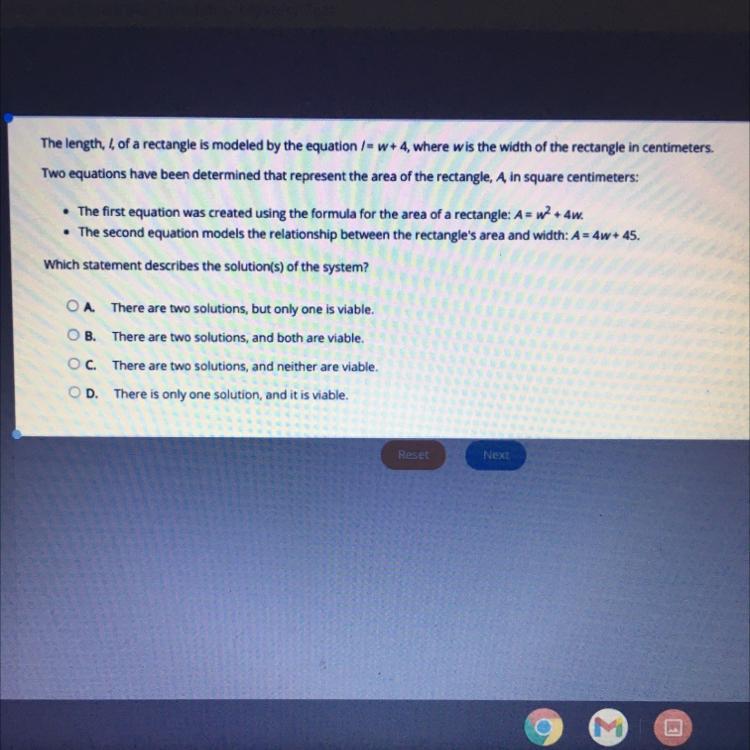
Answers
To solve the given system of equations:
1. Substitute the A by the value given in the other equation (equal the equations):
\(w^2+4w=4w+45\)2. Leave in one side of the equation those terms with the variable w and solve it:
\(\begin{gathered} w^2+4w-4w=45 \\ w^2=45 \\ w=\sqrt[]{45} \\ \\ w_1\approx6.70 \\ w_2\approx-6.70 \end{gathered}\)Then, the system of equations have two solutions.
Since w is the width of a rectangle it cannot be a negative value. Just one of the solutions is viable.
There are two solutions, but only one is viableAlan buys a bag of 13 oranges for $2.99. find the unit price in dollars per orange. I f necessary, round your answer to the nearest cent
Answers
Answer:
23 cents
Step-by-step explanation:
Answer:
0..23
Step-by-step explanation
divide 2.99 by 13
What is 2 x 3/5 + 1/5
Answers
Answer:
its 1.4
Step-by-step explanation:
Answer:
1.4
Step-by-step explanation:
What is the probability of snow on Christmas: is it impossible,unlikely, equally likely, likely, or certain? Pls help i would appreciate it!!
Answers
To determine the probability of snow on Christmas in your area, you would need to examine historical weather data and calculate the percentage of years with snow on that date. Based on that percentage, you can classify the probability into one of the categories above.
To determine the probability of snow on Christmas, you need to consider the location and historical weather data. However, I can explain the terms you've mentioned.
1. Impossible: A probability of 0%, meaning it will never happen.
2. Unlikely: A low probability, but not impossible. It's less than 50% likely to occur.
3. Equally likely: A 50% probability, meaning it's just as likely to happen as not happen.
4. Likely: A high probability, greater than 50%, meaning it's more likely to happen than not.
5. Certain: A probability of 100%, meaning it will definitely happen.
To determine the probability of snow on Christmas in your area, you would need to examine historical weather data and calculate the percentage of years with snow on that date. Based on that percentage, you can classify the probability into one of the categories above.
Learn more about probability
brainly.com/question/30034780
#SPJ11
Which equation is correct regarding the measure of ∠mnp? m∠mnp = one-half(x – y) m∠mnp = one-half(x y) m∠mnp = one-half(z y) m∠mnp = one-half(z – y)
Answers
Answer:
The measure of anle MNP is
m ∠ MNP = (x - y)/2Explanation:
The image attached shows the figure corresponding to this question.
The angle MNP, wich is also the angle LNP, is formed by the intersection of a secant and a tanget to a circle.
Then, you can use the theorem:
the angle formed by a secant and a tangent to a circle that intersect outside the circle is half the difference of the major arc minus the minor arc.The major arc formed is identified with the letter x and the minor arc is identified witht he letter y. Thus, the measure of the angle MNP is half the differenc x - y:
m ∠ MNP = (x - y)/2
Miguel Rodriguez borrowed $300 from his brother Julio to pay for books and tuition. He agreed to pay Julio in 6 months with simple annual interest at 6.5%.
Answers
Answer:
Simple Interest = 9.75
Total Amount needed to payback = 309.75
Step-by-step explanation:
SI = P x R x T / 100
SI = Simple Interest
P = Principal
R = Rate in years
T = Time
SI = 300 x 1/2 x 6.5 /100
=> SI = 3 x 1/2 x 6.5
=> 1.5 x 6.5
=> 9.75
Total Amount needed to payback = Principal + Simple Interest
=> Total Amount needed to payback = 300 + 9.75
=> Total Amount needed to payback = 309.75
State the rule. Then write the next two terms. 240,120,60,
Answers
Answer:
The numbers are being divided by 2 each time.
240/2 = 120
120/2 = 60
So the next set of numbers would be:
30, 15 because
60/2 = 30
30/2 = 15
Step-by-step explanation:
Hope it helps!
Apply the Distributive Property to rewrite 2(6 - x) = 3. Then solve th equation Apply the Distributive Property to rewrite 2(6 - x)= 3. Choose the correct answer below, A. 6(2) – 6X = 3 OB. 2(6) - 2x = 3 OC. 6(2) +GX = 3 ED. 2(6) + 2x = 3
Answers
Answer:
x = ⁹⁄₂ Or 4.5Explanation:
2(6 - x) = 3
Apply Distributive Property2(6 - x) = 3
2(6) = 12, 2(x) = 2x12 - 2x = 312 - 2x = 3
Subtract 12 From Both Sides12 - 2x - 12 = 3 - 12
Simplify-2x = -9
Divide Both Sides By -2-2x / -2 = -9 / -2
Simplifyx = ⁹⁄₂ Or 4.5Answer:
Step-by-step explanation:
C
A poll conducted by the UC Berkeley Institute of Governmental studies in 2019 found that 51.7% of 4527 respondents said they considered moving out of the state.Here n=4527 and p^=51.7=0.517 , andq^=1-p^=1-0.517=0.483Now to compute 95% confidence interval for the proportion of all California who considered moving out of state.
Answers
The 95% confidence interval for the proportion of all Californians who considered moving out of state is (0.504, 0.530). We can be 95% confident that the true proportion of all Californians who considered moving out of state lies between 50.4% and 53.0%.
The UC Berkeley Institute of Governmental Studies conducted a poll in 2019 with 4,527 respondents in California, where 51.7% of them reported considering moving out of the state. The objective is to calculate a 95% confidence interval for the proportion of all Californians who considered moving out of state, given the sample size and proportion.
B. The formula to calculate the confidence interval for a proportion is:
CI = p^ ± z* √[(p^(1-p^))/n]
Where p^ is the sample proportion, n is the sample size, and z* is the critical value of the standard normal distribution for the desired confidence level. For a 95% confidence level, z* = 1.96.
Substituting the given values into the formula, we get:
CI = 0.517 ± 1.96 * √[(0.517*(1-0.517))/4527]
CI = 0.517 ± 0.013
The 95% confidence interval for the proportion of all Californians who considered moving out of state is (0.504, 0.530). Therefore, we can be 95% confident that the true proportion of all Californians who considered moving out of state lies between 50.4% and 53.0%.
For more questions like Sample click the link below:
https://brainly.com/question/31101410
#SPJ11
The volume of a gas V held at a constant temperature in a closed container varies inversely with its pressure P. If the volume of a gas is 800 cubic centimeters when the pressure is 450 millimeters of mercury (mm Hg), find the volume when the pressure is 200 mm Hg.
Answers
SOLUTION:
Step 1:
In this question, we are given the following:
The volume of a gas V held at a constant temperature in a closed container varies inversely with its pressure P. If the volume of a gas is 800 cubic centimeters when the pressure is 450 millimeters of mercury (mm Hg), find the volume when the pressure is 200 mm Hg.
Step 2:
This is an application of Boyle's law which states that:
Boyle’s law is a gas law that states that the pressure exerted by a gas (of a given mass, kept at a constant temperature) is inversely proportional to the volume occupied by it. In other words, the pressure and volume of a gas are inversely proportional to each other as long as the temperature and the quantity of gas are kept constant.
\(\begin{gathered} Mathematically,\text{ we have that:} \\ V\text{ }\propto\text{ }\frac{1}{P} \\ Then,\text{ we have that:} \\ V\text{ =}\frac{k}{P}\text{ \lparen where k is a constant \rparen} \end{gathered}\)\(when\text{ V = 800 cubic centimetres , then P = 450 mm Hg}\)\(\begin{gathered} 800\text{ =}\frac{k}{450} \\ cross-multiply,\text{ we have that:} \\ \text{k = 800 x 450 = 360,000} \end{gathered}\)\(\begin{gathered} Then,\text{ the equation connecting V and P =} \\ \text{ V }=\frac{360,000}{P} \end{gathered}\)Next:
\(when\text{ P = 200 mm Hg, we have that:}\)\(\begin{gathered} V\text{ = }\frac{360,000}{200} \\ \text{V = 1800 cubic centimetres } \end{gathered}\)CONCLUSION:
The volume when the pressure is 200 mm Hg is:
\(V\text{ = 1800 cubic centimetres}\)Solve the diamond problem.

Answers
7 and and -12 is the answer correct me if im wrong
HOPE IT HEPLS:)