The length of a rectangle is twice the width. The area is 162 yd? Find the length and the width.
The length is yd.
(SimplifyJyour answer.)
Answers
Answer:
length = 2x = 2(9) = 18 yds
Step-by-step explanation:
Let width = x
Let length = 2x
Area = 162 yd2
length × width = Area
2x(x) = 162
2x2 = 162
Divide by 2 on both sides of equation.
x2 = 81
Square-root both sides of equation to undo the exponent.
x = √(81)
x = 9
Substitute this x value into the initial variables.
width = x = 9 yds
length = 2x = 2(9) = 18 yds
Related Questions
The flower box is 5 ft long, and its ends are in the shape of a trapezoid. The upper and lower bases of the trapezoid measure 18 in. and 10 in., respectively, and the height is 9 in. Find the volume of the flower box.
Answers
The volume of the flower box is 7560 cubic inches
How to determine the volume of the box?The given parameters in the question are:
Length = 5 ft
Upper and lower bases = 18 inches and 10 inches
Height = 9 inches
The volume of the box can be calculated using the following volume equation
Volume = 0.5 * Height * Length * (Sum of the bases)
Substitute the known values in the above equation So, we have the following equation
Volume = 0.5 * 9 inches * 5 feet * (18 inches + 10 inches)
Convert feet to inches
Volume = 0.5 * 9 inches * 60 inches * (18 inches + 10 inches)
Evaluate
Volume = 7560 cubic inches
Hence, the volume is 7560 cubic inches
Read more about volume at
https://brainly.com/question/463363
#SPJ1
Which of the following is the correct factorization of the polynomial below? 8x3 + 64y3 A. (4x + 4y) (2x+8y) B. (2x + 4y)(4x2 - 8xy + 16y2) C. (4x + 2y)(4x2 - 2xy + 16y?) D. The polynomial is irreducible.
Answers
Answer:
B. (2x+4y)(4x2-8xy+16y2)
Step-by-step explanation:
hope this helps!
A ball is dropped from a height of 20 feet. Each time the ball bounces it returns to 7/9 of the height it fell from. Let an represent the maximum height of the ball on the nth bounce.
A) Find a formula that describes an. Express the common ratio as a fraction. Hint: Use an = a1r^n-1 and place r in parentheses!
an = _____________
B) What is the maximum height of the ball on the 6th bounce? Round your answer to three decimal places.
_______________ feet
Answers
a) The formula that describes the geometric sequence is of:
\(a_n = 20\left(\frac{7}{9}\right)^{n - 1}\)
b) The maximum height on the 6th bounce is of: 5.69 feet.
What is a geometric sequence?The definition of a geometric sequence is given by the equation presented as follows:
\(a_n = a_1(r)^{n - 1}\)
Which is used to calculate the nth term of the sequence.
In which the parameters of the equation are given as follows:
\(a_1\) is the first term.r is the common ratio of the sequence.From the description in the text, the first term and the common ratio of the sequence are given as follows:
\(a_1 = 20, r = \frac{7}{9}\)
Then the formula that defines the sequence is given as follows:
\(a_n = 20\left(\frac{7}{9}\right)^{n - 1}\)
The maximum height, in feet, after the 6th bounce is given as follows:
\(a_6 = 20\left(\frac{7}{9}\right)^{6 - 1} = 5.69\)
More can be learned about geometric sequences at https://brainly.com/question/24643676
#SPJ1
In ΔFGH, h = 840 inches, � m∠F=93° and � m∠G=49°. Find the length of g, to the nearest 10th of an inch.
Answers
Let's use the formula:
g / sin(G) = h / sin(H)
Substituting the given values:
g / sin(49°) = 840 / sin(93°)
Now, we can solve for g. Rearranging the equation, we have:
g = (sin(49°) * 840) / sin(93°)
Using a calculator, we can evaluate this expression to find the approximate length of g.
g ≈ (0.7502 * 840) / 0.9998
g ≈ 630.168 / 0.9998
g ≈ 630.227
Therefore, the length of side g, rounded to the nearest tenth of an inch, is approximately 630.2 inches.
Write a function rule for

Answers
Answer:
x^2
Step-by-step explanation:
1^2=1
2^2=4
3^2=9
Daniel bought a pokemon card at a store for $10. He sold the card for $20.
Later he bought the same card back for $30 and then sold it again for $50.
How much money did he make or lose on the pokemon card?
Answers
Answer:
Daniel gained 30 dollars.
Step-by-step explanation:
-10 + 20 = 10
10 - 30 = -20
-20 + 50 = 30
Hope this helps :)
when you do the graph part can you write on my picture, please?
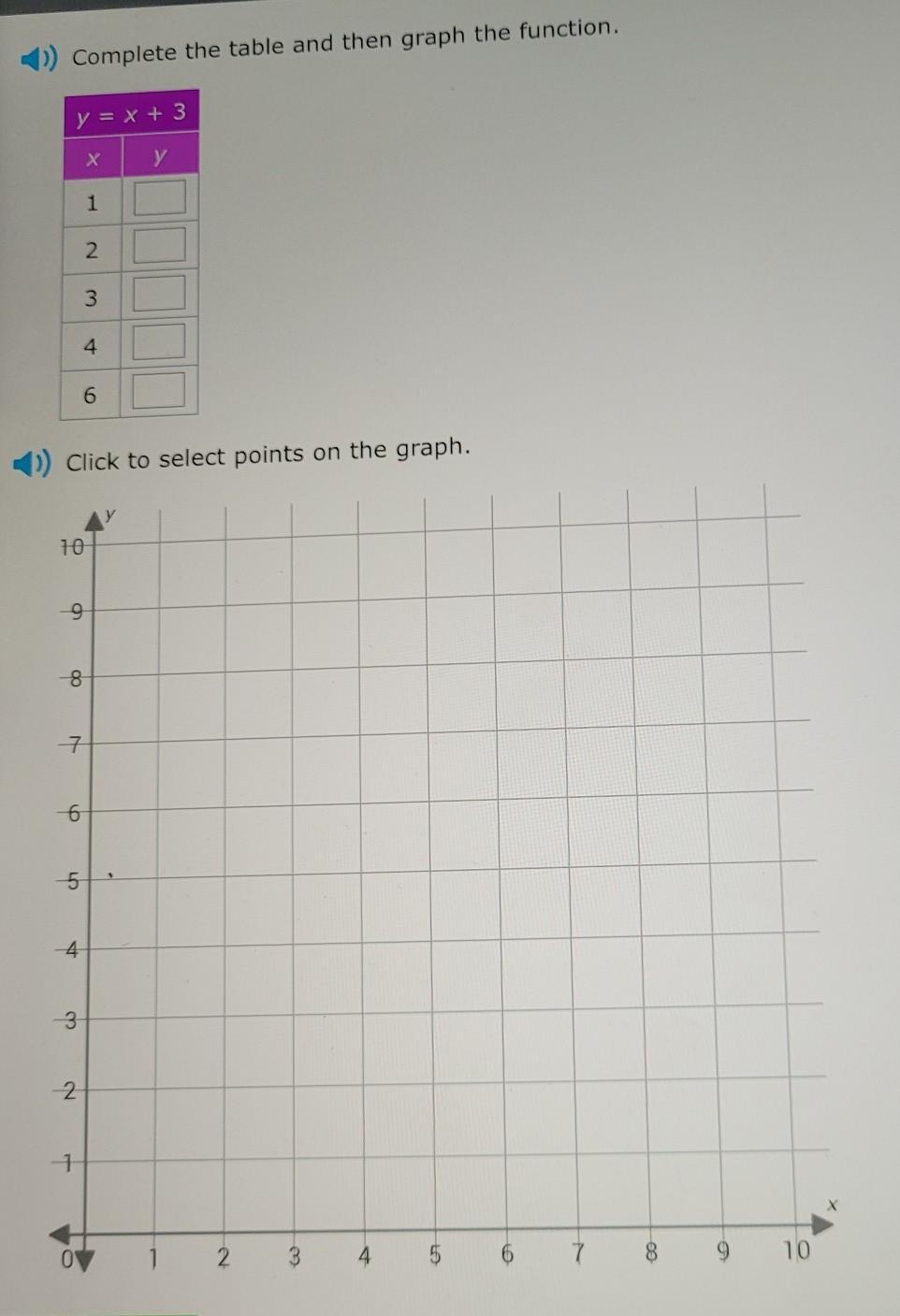
Answers
Given that y = x + 3
Find the value of y when x = 1, 2, 3, 4, 5, and 6
For x = 1
y = 1 + 3
y = 4
For x = 2
y = 2 + 3
y = 5
For x = 3
y = 3 + 3
y = 6
For x = 4
y = 4 + 3
y = 7
For x = 5
y = 5 + 3
y = 8
For x = 6
y = 6 + 3
y = 9
Hence, the table can be filled as follows
x y
1 4
2 5
3 6
4 7
5 8
6 9
The next thing is to graph it on a graph

Given the following five-number summary, find Q₁.
2.9, 5.7, 10.0, 13.2, 21.1
OA. 5.7
OB. 2.9
OC. 10.0
Answers
Given the following five-number summary: 2.9, 5.7, 10.0, 13.2, 21.1, so Q₁ = 5.7. This can be solved using the concept of quartile.
What is quartile?A kind of percentile is a quartile. The first quartile (Q₁, or the lowest quartile), which corresponds to the 25th percentile of the data, is below which 25% of the data are found. The second quartile (Q₂, or the median), which represents the 50th percentile, indicates that 50% of the data are below this quartile.
There are 5 data points, and the middle value of the lower half of the data set will represent the first quartile. So the second data value is the first quartile. So, Q₁ = 5.7
There are 5 data points, and the middle value of the upper half of the data set will represent the third quartile. The fourth data value is the third quartile. So,
Q₃ = 13.2
SO IQR will be:
= Q₃ - Q₁
= 13.7 - 5.1
= 7.5
Thus, Q₁ = 5.7
To know more about quartile refer to:
https://brainly.com/question/28169373
#SPJ1
Solve for x: ( 1/2 )^(x−1)=2^(3x−4)
Answers
Answer:
\(\huge\boxed{x=\dfrac{5}{4}}\)
Step-by-step explanation:
\(\left(\dfrac{1}{2}\right)^{x-1}=2^{3x-4}\qquad\text{use}\ a^{-1}=\dfrac{1}{a}\\\\\left(2^{-1}\right)^{x-1}=2^{3x-4}\qquad\text{use}\ (a^n)^m=a^{nm}\\\\2^{(-1)(x-1)}=2^{3x-4}\qquad\text{use the distributive property}:\ a(b+c)=ab+ac\\\\2^{(-1)(x)+(-1)(-1)}=2^{3x-4}\\\\2^{-x+1}=2^{3x-4}\iff-x+1=3x-4\qquad\text{subtract 1 from both sides}\\\\-x+1-1=3x-4-1\\\\-x=3x-5\qquad\text{subtract}\ 3x\ \text{from both sides}\\\\-x-3x=3x-3x-5\\\\-4x=-5\qquad\text{divide both sides by (-4)}\)
\(\dfrac{-4x}{-4}=\dfrac{-5}{-4}\\\\x=\dfrac{5}{4}\)
A solid machine part is to be manufactured as shown in the figure. The part is made by cutting a small cone off the top of a larger cone. The small cone has a base radius of 3 inches and a height of 5 inches. The larger cone has a base radius of 9 inches and had a height of 15 inches prior to being cut. What is the volume
Answers
Answer:
The answer is 390 × pi.
Step-by-step explanation:
Big cone:
V = 1/3 x pi x r^2 x h
= 1/3 x 3.14 x 9^2 x 15
= 1272.3 cubic inches
Small cone:
V = 1/3 x pi x r^2 x h
= 1/3 x 3.14 x 3^2 x 5
= 47.1 cubic inches
1272.3 - 47.1 = 1225.2 cubic inches
1272/3.14 ≈ 390
The answer is 390 × pi.
kevin scored a 4 over par (+4) on the first nine holes of the golf course. What does he need to score over the last nine holes to get back to a even par (0)?
Answers
Answer:
6
Step-by-step explanation:
he needs 6 points to score over the last nine holes
Kevin needs to score 8.5 strokes per hole for the last nine holes to get back to an even par.
What is Algebra?A branch of mathematics known as algebra deals with symbols and the mathematical operations performed on them.
We can find the total number of strokes Kevin needs to score over 18 holes to reach an even par.
If the par score for 18 holes is 72,
and Kevin scored 4 over par on the first nine holes
= 9 × 4 = 36 extra strokes.
Now, if the par score for the last nine holes is x, then we have:
4 + x + x + x + x + x + x + x + x = 72
4 + 8x = 72
8x = 68
x = 8.5
Therefore, Kevin needs to score 8.5 strokes per hole for the last nine holes to get back to an even par.
Learn more about Algebra here:
https://brainly.com/question/24875240
#SPJ2
Yavonne has $15.90 in her checking account. She needs to buy items that cost $3.18 each. How many of these items can she buy?
a
4
b
5
c
6
d
7
Answers
Answer:
5.
Step-by-step explanation:
15.90 / 3.18 =
f(x)= a(x+p)² +q and g(x)= 0 3 3.1 x + p 1. The turning point of f is (1;4) and the asymptotes of g intersect at the turning point of f. Both graphs cut the y-axic at 3. 3.2 3.3 3.4 a 10 g +94 (1:4) Determine the equation of f Determine the equation of g Determine the coordinates of the x-intercept of g For which values of x will f(x) ≥ g(x)? [9]
Answers
Step-by-step explanation:
Let's solve the given questions step by step:
1. Determine the equation of f:
From the given information, we know that the turning point of f is (1, 4). The general form of a quadratic function is f(x) = ax^2 + bx + c. We are given that f(x) = a(x + p)^2 + q, so let's substitute the values:
f(x) = a(x + p)^2 + q
Since the turning point is (1, 4), we can substitute x = 1 and f(x) = 4 into the equation:
4 = a(1 + p)^2 + q
This gives us one equation involving a, p, and q.
2. Determine the equation of g:
The equation of g is given as g(x) = 0.3x + p1.
3. Determine the coordinates of the x-intercept of g:
The x-intercept is the point where the graph of g intersects the x-axis. At this point, the y-coordinate is 0.
Setting g(x) = 0, we can solve for x:
0 = 0.3x + p1
-0.3x = p1
x = -p1/0.3
Therefore, the x-intercept of g is (-p1/0.3, 0).
4. For which values of x will f(x) ≥ g(x)?
To determine the values of x where f(x) is greater than or equal to g(x), we need to compare their expressions.
f(x) = a(x + p)^2 + q
g(x) = 0.3x + p1
We need to find the values of x for which f(x) ≥ g(x):
a(x + p)^2 + q ≥ 0.3x + p1
Simplifying the equation will involve expanding the square and rearranging terms, but since the equation involves variables a, p, and q, we cannot determine the exact values without further information or constraints.
To summarize:
We have determined the equation of f in terms of a, p, and q, and the equation of g in terms of p1. We have also found the coordinates of the x-intercept of g. However, without additional information or constraints, we cannot determine the exact values of a, p, q, or p1, or the values of x for which f(x) ≥ g(x).
The milligrams of aspirin in a person's body is given by the equation a = 500*(3/4^t), where t is the number of hours since the patient took the medicine.
In the equation, what does 500 tell us about the situation?
SOMEONE ANSWER PLS!!
Answers
500 represents the initial amount of medication, since when t=0, a=500.
please help meeeeeee

Answers
Answer: That would be distributive
Step-by-step explanation:
The conditional statement below is true. If possible, write the biconditional statement.
If 2x = 18, then x = 9.
Answers
The biconditional statement for the given conditional statement would be:
2x = 18 if and only if x = 9.
The given conditional statement "If 2x = 18, then x = 9" can be represented symbolically as p → q, where p represents the statement "2x = 18" and q represents the statement "x = 9".
To form the biconditional statement, we need to determine if the converse of the conditional statement is also true. The converse of the original statement is "If x = 9, then 2x = 18". Let's evaluate the converse statement.
If x = 9, then substituting this value into the equation 2x = 18 gives us 2(9) = 18, which is indeed true. Therefore, the converse of the original statement is true.
Based on this, we can write the biconditional statement:
2x = 18 if and only if x = 9.
The biconditional statement implies that if 2x is equal to 18, then x must be equal to 9, and conversely, if x is equal to 9, then 2x is equal to 18. The biconditional statement asserts the equivalence between the two statements, indicating that they always hold true together.
In summary, the biconditional statement is a concise way of expressing that 2x = 18 if and only if x = 9, capturing the mutual implication between the two statements.
for such more question on conditional statement
https://brainly.com/question/27839142
#SPJ8
The pentagonal prism below has a base area of 36 units and a volume of 237.6 units . Find its height.
Answers
The height of the pentagonal prism is approximately 2.94 units
The formula for the volume of a pentagonal prism is;
V = (1/2) × base_area × height × (1 + √(5))
where base_area is the area of the base of the prism, height is the height of the prism, and sqrt(5) is the square root of 5.
In this problem, we are given that the base area is 36 units and the volume is 237.6 units. We can use this information to set up an equation and solve for the height;
237.6 = (1/2) × 36 × height × (1 + √(5))
Dividing both sides by (1/2) × 36 × (1 + √(5)), we get;
height = 237.6 / [18 × (1 + √(5))]
Simplifying this expression, we get;
height = 4.8 / (1 + √(5))
Rationalizing the denominator by multiplying both the numerator and denominator by (√(5) - 1), we get;
height = [4.8 × (√(5) - 1)] / [4]
Simplifying further, we get;
height = 1.2 × √(5) - 1)
height = 2.94 units
Therefore, the height is 2.94 units
To know more about pentagonal prism here
https://brainly.com/question/26709266
#SPJ1
A recipe calls for 2 cup of brown sugar for every 6 cups of white sugar. How many cups of brown sugar are required for every 12 cups of white sugar?
(PLEASE HELP!!)
Answers
There are 4 cups of brown sugar are required for every 12 cups of white sugar.
A recipe calls for 2 cups of brown sugar for every 6 cups of white sugar. We can set up a proportion to find the relationship between the two quantities:
2 cups brown sugar / 6 cups white sugar = x cups brown sugar / 12 cups white sugar
To find the number of cups of brown sugar required for 12 cups of white sugar, we can cross-multiply and then solve for x:
2 cups brown sugar × 12 cups white sugar = 6 cups white sugar × x cups brown sugar
24 cups brown sugar = 6x cups brown sugar
x = 24/6
x = 4
So, 4 cups of brown sugar are required for every 12 cups of white sugar.
Learn more about the proportion here:
brainly.com/question/1504221
#SPJ1
If you pick a card from a standard deck find the following probabilities 1. P(odd number card or king) =2. P(red card or face card) =Make sure your answer is in reduce fraction form and no work is needed in answer space
Answers
Assuming that:
There are a total of 52 cards in a deck.
Numbers 2 through 10
Face card: jack, queen and king.
P(odd number card or king):
Odd number = 4
King = 4
\(P(\text{odd number card or king) = }\frac{odd\text{ number + king}}{\text{total}}\text{=}\frac{4+4}{52}=\frac{8}{52}\approx\text{ 0.15}\)P(odd number card or king)= 0.15
P(red card or face card):
Red card = 13 X 2 = 26
Face card ( jacks, queens, and kings) = 4 + 4 + 4 = 16
\(P(\text{red card or face card)}=\frac{red\text{ cards + face card}}{\text{Total}}=\frac{26+16}{52}=\frac{42}{52}\approx0.81\)P(red card or face card) = 0.81
O MEASUREMENT Unit conversions involving acres and hectares After she retired, a corporate executive moved to wine country and bought a 326.7 acre (ac) vineyard. Use the facts to find the area of the vineyard in square feet (ft²). OA² X Conversion facts for area 1 acre (ac) = 43,560 square feet (t²) 1 square mile (mi²) = 640 acres (ac) 1 hectare (ha) 2.5 acres (ac) Note that means "is For this problem, treat as if it were =. approximately equal to".
Answers
Answer:
oaw2 232 acre is 468688$
Step-by-step explanation:
O MEASUREMENT Unit conversions involving acres and hectares After she retired, a corporate executive moved to wine country and bought a 326.7 acre (ac) vineyard. Use the facts to find the area of the vineyard in square feet (ft²). OA² X Conversion facts for area 1 acre (ac) = 43,560 square feet (t²) 1 square mile (mi²) = 640 acres (ac) 1 hectare (ha) 2.5 acres (ac) Note that means "is For this problem, treat as if it were =. approximately equal to".
3 1/2 divided 2 3/5 in its simplest form
Answers
Answer:
9.1 is answer or 91/10 or 9 1/10
The area of a rectangle is 40 square inches. The rectangle is 8 inches long. How wide is the rectangle?
A. 3 inches
B. 32 inches
C. 5 inches
D. 13 inches
Answers
Answer:
C. 5 inches
Step-by-step explanation:
I’m area you have to multiply L • W
But since we don’t know the width we can divide the length by the area.
40/8 = 5
So the answer would be 5.
Another way to solve this problem is with using guess and check.
I hope it helps! Have a great day!
Anygays~
Answer:
C. 5 inches
Step-by-step explanation:
Use the numbers we have in the word problem, so you´d divide 40 by 8 since you´re trying to find the width. 40 is the area and 8 is the length so divide it tofind the width.
40/8 = 5
ANSWER: 5 inches
I hope it helps! Have a great day!
A rancher has 200 feet of fencing to enclose two adjacent rectangular corrals. What dimensions should
be used so that the enclosed area will be a maximum?
Answers
Length is 33.33 feet and width is 25 feet are dimensions should
be used so that the enclosed area will be a maximum.
What is Area of Rectangle?The area of Rectangle is length times of width
Given that, a rancher has 200 feet of fencing to enclose two adjacent rectangular corrals of the same dimensions.
Here, the dimensions of the rectangles are the same.
The width of the two rectangles is W=2W+2W=4W
The length of the two rectangles is L=L+L+L=3L
Because the adjacent side has a common length.
3L+4W=200
3L=200-4W
Divide both sides by 3
L=(200-4W)/3
Let us form an equation using the area of rectangle formula:
A=2LW
=2(200-4W)/3.W
A=400-8W²/3
Let us differentiate to get the area to be maximized dA/dW=0
1/3×(400-8W²)=0
1/3(400-16W)=0
400-16W=0
400=16W
Divide both sides by 16
W=25
The width is 25 feet.
Substitute W value in equation to get L value:
L=200-4×25/3
=200-100/3
=100/3
=33.33
The length is 33.33 feet.
Now let us find the maximum area
A=2LW
=2×33.33×25
=1666.66
Hence, length is 33.33 feet and width is 25 feet are dimensions should
be used so that the enclosed area will be a maximum.
To learn more on Rectangle click:
https://brainly.com/question/20693059
#SPJ1
what is the value of x in the equation 6x-5/2 = 2x+6
Answers
Answer:
x= 17/8
Step-by-step explanation:
6x− 5/2=2x+6
Step 1: Simplify both sides of the equation.
6x+−5/2=2x+6
Step 2: Subtract 2x from both sides.
6x+−5/2−2x=2x+6−2x
4x+−5/2=6
Step 3: Add 5/2 to both sides.
4x+−5/2+5/2=6+5/2
4x=17/2
Step 4: Divide both sides by 4.
4x/4=17/2/4
x=17/8
Is 10 pints greater less or equal to 5 quarts
Answers
Answer:
10 pints is equal to 5 quarts
Step-by-step explanation:
30 POINTS!!!!! URGENT!

Answers
Step-by-step explanation:
Average daily balance: Add all balances up and divide by the number of days.
157.63*9+239.98*1+239.98*4+180.38*1+180.38*9+190.57*1+190.57*6 gives us our total of 5756.36, and there were 9+1+4+1+9+1+6=31 days, so 5756.36/31 gives us our average of 185.69, or the fourth option
Daily interest rate: 24.99/365, as a percent, which is the first option
Finance charge: This is the cost of borrowing, and does not seem to be given, so we can take it to be the lowest amount, or the third value
New account balance: Again, this does not seem to be given, but the only option remaining is the second one
Answer:
Average daily balance: Add all balances up and divide by the number of days.
157.63*9+239.98*1+239.98*4+180.38*1+180.38*9+190.57*1+190.57*6 gives us our total of 5756.36, and there were 9+1+4+1+9+1+6=31 days, so 5756.36/31 gives us our average of 185.69, or the fourth option
Daily interest rate: 24.99/365, as a percent, which is the first option
Finance charge: This is the cost of borrowing, and does not seem to be given, so we can take it to be the lowest amount, or the third value
New account balance: Again, this does not seem to be given, but the only option remaining is the second one
m
Step-by-step explanation:
what is the answers to this question

Answers
By evaluating the quadratic equation, we will see that the values of the expressions are:
f(-1) + f(4) = 27
f(-1) - f(4) = -35
How to evaluate the given expressions?Here we need to work with the quadratic function:
f(x) = x^2 + 6x + 1
First, we want to find the value of the expression:
f(-1) + f(4)
To get that, we need to evaluate the quadratic equation:
f(-1) = (-1)^2 + 6*(-1) + 1
f(-1) = 1 - 6 + 1 = -4
f(4) = 4^2 + 6*4 + 1
f(4) = 16 + 24 + 1 = 31
Then the first expression is:
f(-1) + f(4) = -4 + 31 = 27
The second expression is:
f(-1) - f(4)
We already know these values, we can replace these to get:
f(-1) - f(4) = -4 - 31 = -35
Learn more about quadratic equations at:
https://brainly.com/question/1214333
#SPJ1
Plato!!! Please help ~_~
Type the correct answer in the box. If necessary, use / for the fraction bar.
A solid wooden block in the shape of a rectangular prism has a length, width, and height of 3/8 centimeter, 1/8 centimeter, and 5/8 centimeter,
respectively,
The volume of the block is (——)
cubic centimeter.
The number of cubic wooden blocks with a side length of 1/8 centimeter that can be cut
from the rectangular block is(—)
Answer goes in the (—)
Answers
Answer:
V = 3/8 * 1/8 * 5/8 cm^3 = 15 / 512 cm^3
Since all sides are evenly divisible by 1/8 and v = (1 / 8)^3 = 1 / 512 cm^3
N = V / v = (15 / 512) / (1 / 512) = 15 blocks
Example: cut 1/8 by 5/8 into 5 blocks
Cutting 1/8 by 5/8 could be done 3 times for a total of 15 blocj\ks
express 2 cos 35 sin 67 as a sum
Answers
2 cos 35 sin 67 can be expressed as the sum of sin(102) and -sin(32).
To express 2 cos 35 sin 67 as a sum, we can use the trigonometric identity for the product of two sine or cosine functions.
Specifically, the identity states that 2 cos A sin B can be written as
sin(A + B) + sin(A - B).
Applying this identity, we have:
2 cos 35 sin 67 = sin(35 + 67) + sin(35 - 67)
Simplifying the expressions inside the sine functions:
sin(102) + sin(-32)
Since the sine function is an odd function,
sin(-x) = -sin(x),
so we can rewrite the equation as:
sin(102) - sin(32)
Therefore, 2 cos 35 sin 67 can be expressed as the sum of sin(102) and -sin(32).
For such more questions on trigonometric identity
https://brainly.com/question/7331447
#SPJ8
HELP! Whoever gets it right gets brainliest!!
