The graph below compares life expectancy in years and the average number of cigarettes smoked per day .What type of trend line would best fit the data? O a horizontal line O a line with a positive slope O a line with a negative slope O no trend line
Answers
According to the given graph, the type of trend line that would best fit is a line with a negative slope. The graph clearly shows a linear relationship, and given that it's going down, we deduct that its slope is negative.
Hence, the answer is C.Related Questions
Geometry 50 pts: finding x,y,z in the shape below. I think I have x and y right, im just not sure how to solve z. Please let me know if any are wrong c: I'd also like an explanation so I can do it in the future.
Thank you!!
(I also ask that I don't get another person answering and taking the points just to say 'I don't know, I tried couldn't do it') thanks!!

Answers
The value of x in the figure is 6
What is a parallelogram?A parallelogram is a special type of quadrilateral that has both pairs of opposite sides parallel and equal
The two opposite sides of the parallelogram that bear x are
2x-3 = 5x-21
Collecting similar terms we have
2x-5x = -21 +3
2x-5x = -21 +3
-3x = -18
Making x the subject of the formula
Hence x = 6
Learn more about a parallelogram on https://brainly.com/question/29147156
#SPJ1
in chess, the knight (the piece shaped like a horse) moves in an L pattern.
Answers
Answer:
That is true but still remember that playing the knight at the start can be very useful.
Y’all got on Brainly quick it’s only Wednesday
Answers
Answer:
some ppl got summer school
Step-by-step explanation:
For two n by n square matricies A and B,
suppose rankA = rankB = n-1.
Can rank(AB) become less than n-1 ?
(e.g. rank (AB) = n-2)
If so, I humbly ask you for an example.
Thank you very much.
Answers
No, the rank of the product of two n by n square matrices A and B, denoted as AB, cannot be less than n-1 if both A and B have ranks of n-1.
According to the Rank-Nullity theorem, for any matrix M, the sum of its rank and nullity is equal to the number of columns in M. In this case, the number of columns in AB is n, so the sum of the rank and nullity of AB must be n.
If rank(A) = rank(B) = n-1, it means that both A and B have nullity 1. The nullity of a matrix is the dimension of its null space, which consists of all vectors that get mapped to the zero vector when multiplied by the matrix. Since both A and B have rank n-1, their null spaces consist only of the zero vector.
Now, considering AB, if the rank of AB were less than n-1, it would mean that the nullity of AB is greater than 1.
However, this would violate the Rank-Nullity theorem since the sum of the rank and nullity of AB must be n, which is the number of columns.
Therefore, if rank(A) = rank(B) = n-1, the rank of AB cannot be less than n-1.
For more such questions on rank
https://brainly.com/question/28839672
#SPJ8
who is right andrew or annie?

Answers
Answer:
andrew
Step-by-step explanation:
Find the Surface Area of the following figure. 9.5 m 16m 14m 12.7m 11m
Answers
The total surface area of the figure will be 1968.85 square meters.
To determine the surface area of the figure, we need to find the area of each face and then add them together.
Surface Area of the rectangular prism = 2(lb + bh + hl)
= 2(16 × 9.5) + 2(9.5 × 14) + 2(16 × 14)
= 2(152 + 133 + 224) = 2(509)
= 1018 m²
Next, we need to find the area of the triangular prism on the front with dimensions 11 m, 12.7 m, and 14 m:
Surface Area of the triangular prism;
= (11 × 14) + 2(0.5 × 11 × 12.7) + 2(0.5 × 12.7 × 14)
= (154 + 350.35 + 445.5)
= 950.85 m²
Therefore, the total surface area of the figure will be;
Total Surface Area = Surface Area of rectangular prism + Surface Area of triangular prism
= 1018 m² + 950.85 m²
= 1968.85 m²
So, the surface area of the figure is 1968.85 square meters.
Learn more about a rectangular prism;
https://brainly.com/question/21308574
#SPJ1
PLEASE HELPP ASAPPP pleaseeeee

Answers
answer: 28561^2in the area involves multiplying by the 4 sides of the shaded square and the shaded is the colored square.
Can someone help me?

Answers
Answer:
hi I can't open the photo
Help Please solve this Below!!! Lots of points and brainliest!!! I need it done now!!!a
Solve for C in the following equation. DO not caculate numerical values.

Answers
Answer:
\(c=\sqrt{\frac{2 \pi^5k^4}{15 \sigma h^3}}.\)
Step-by-step explanation:
\(if \ \sigma=\frac{2 \pi^5k^4}{15c^2h^3} , \ then\\\\c^2=\frac{2 \pi^5k^4}{15h^3 \sigma}.\)
finally,
\(c=\sqrt{\frac{2 \pi^5k^4}{15 \sigma h^3}} \ or \ c=\frac{\pi^2k^2}{h} \sqrt{\frac{2 \pi}{15h \sigma} } .\)
Need help quick please

Answers
Answer:-1/6
Step-by-step explanation:
Draw a line out in the 2nd quadrant.
Your y=\(\sqrt{35}\) hypotenuse=6 use pythagorean theorem to solve for x
6² = 35 + x²
x=1
so
cosΘ = -1/6
Ben is reading a book. Rounded to the nearest ten, he reads 150 pages. What is the least number of pages he could read?
Answers
Ben read at least 145 pages.
Ben read book , rounded to the nearest ten , 150 pages.
What is rounding off of a number?
Rounding off means a number is made simpler by keeping its value intact but closer to the next number.
Now,
We know that below the number 145 we cannot round it 150 for rounding of nearest ten.
Therefore, 145 is the smallest number which can be rounded (nearest ten) to 150.
Thus, he could read at least 145 pages.
Learn more about the Rounding off visit:
https://brainly.in/question/5838592
#SPJ2
-8/9 + (-2)/57
find the absolute value of the following rational number
Answers
The absolute value of the Rational number -474/513 is 474/513.
To find the sum of the rational numbers -8/9 and -2/57, you need to have a common denominator. The least common multiple (LCM) of 9 and 57 is 513. So, you can rewrite the fractions with a common denominator:
-8/9 = (-8/9) * (57/57) = -456/513
-2/57 = (-2/57) * (9/9) = -18/513
Now, you can add the fractions:
-456/513 + (-18/513) = (-456 - 18)/513 = -474/513
To find the absolute value of the rational number -474/513, you simply ignore the negative sign and take the value as positive:
| -474/513 | = 474/513
Therefore, the absolute value of the rational number -474/513 is 474/513.
For more questions on Rational .
https://brainly.com/question/30339525
#SPJ8
Which of the following lists of ordered pairs is a function? A. (1,8), (2, 9), (3, 10), (3, 11) B. (-1,4), (1,7), (2, 10) C. (3,7),(4, 5), (3, 8) D. (-2,3), (1, 3), (3, 7), (1, 4)
Answers
Answer:
B
Step-by-step explanation:
B is the only one that doesnt share x-values
On their most recent 8-mile training run, Pepe averaged a speed of 12 of a mile in 4.5 minutes, while Paula averaged 34 of a mile in 7.5 minutes.
How many minutes did it take the faster runner to finish the 8 mile run
Answers
Answer:
1.78 min
Step-by-step explanation:
so first you have to figure out the fastest runner
pepe 12 miles in 4.5 minutes
and paula ran 34 miles in 7.5 minutes
if you divide miles by minutes you get how many miles they ran in one minute
12/4.5=~2.67
34/7.5=~4.53
So you can see that paula is faster
if she ran ~4.5 miles in a minute then it would take her ~1.78 minutes to run 8 miles
they're both super humans though like woah
What are the x intercept and y intercept of the graph 12x-4y=4
Answers
Suppose that P dollars in principal is invested for t years at the given interest rates with continuous compounding. Determine the amount that the investment is worth at the end of the given time period.
=P$10,000, =t112 yr
(a) 1% interest
(b) 4% interest
(c) 4.5% interest
Answers
Answer: (a )$30648.54 (b)$882,346.73 (c) $1,544,700.15
Step-by-step explanation:
Formula: \(A=Pe^{rt}\) , where P= principal , r=rate of interest, t= time
Given : P= $10,000, t = 112 years
(a) r = 1% = 0.01
\(A=(10000)e^{0.01\times112}\)
\(A=(10000)e^{1.12}=10000(3.06485420)\approx 30648.54\)
Hence, Amount = $30,648.54
(b) r = 4% = 0.04
\(A=(10000)e^{0.04\times112}\)
\(A=(10000)e^{4.48}=10000(88.2346726757)\approx 882346.73\)
Hence, Amount = $882,346.73
(c) r = 4.5% = 0.045
\(A=(10000)e^{0.045\times112}\)
\(A=(10000)e^{5.04}=10000(154.470015026)\approx 1544700.15\)
Hence, Amount = $1,544,700.15
The first steps in writing f(x) = 4x2 + 48x + 10 in vertex form are shown. f(x) = 4(x2 + 12x) + 10 (twelve-halves) squared = 36 What is the function written in vertex form?
Answers
Answer:
\(f(x)=4(x+6)^2-134\)
Step-by-step explanation:
We are required to write the function\(f(x) = 4x^2 + 48x + 10\) in vertex form.
First, bring the constant to the left-hand side.
\(f(x) -10= 4x^2 + 48x\)
Factorize the right hand side.
\(f(x) -10= 4(x^2 + 12x)\)
Take note of the factored term(4) and write it in the form below.
\(f(x) -10+4\Box= 4(x^2 + 12x+\Box)\)
\(\Box = (\frac{\text{Coefficient of x}}{2} )^2\\\\\text{Coefficient of x}=12\\\\\Box = (\frac{12}{2} )^2 =6^2=36\)
Substitute 36 for the boxes.
\(f(x) -10+4\boxed{36}= 4(x^2 + 12x+\boxed{36})\)
\(f(x) -10+144= 4(x^2 + 12x+6^2)\)
\(f(x) +134= 4(x+6)^2\\f(x)=4(x+6)^2-134\)
The function written in vertex form is \(f(x)=4(x+6)^2-134\)
Answer:
C
Step-by-step explanation:
I just finished the unit test on Edge. and got a 100% and I selected "c" as my answer.
Solve the inequality below.
2x < 12
Answers
To solve the inequality 2x < 12, we need to isolate x on one side of the inequality sign. We can do this by dividing both sides by 2:
2x < 12
x < 6
Therefore, the solution to the inequality is x < 6. This means that all values of x that are less than 6 satisfy the inequality. We can represent this graphically on a number line:
<=======()------6-------------->
The open circle () indicates that x cannot be equal to 6, but can be any value less than 6. The arrow indicates that the inequality is true for all values of x to the left of the open circle.
In summary, the solution to the inequality 2x < 12 is x < 6.
I'm 15 BTW
Renata is purchasing a condominium for $125,000. She wants to put down a down payment of 20%. Select all the true statements. The proportion that represents the down payment is 20100=125,000 20 100 = 125 , 000 x . The down payment is $25,000. The proportion that represents the down payment is 20100=125,000 20 100 = x 125 , 000 . The down payment is $50,000. The down payment is 15 1 5 of the cost of the house.
Answers
The correct options are -
The proportion that represents the down payment is : 20/100 x 125000.The down payment is $25,000What is down payment?When something is bought on credit, an initial payment is made in the form of a down payment.
Given is that Renata is purchasing a condominium for $125,000. She wants to put down a down payment of 20%.
We can calculate the amount she is putting in down payment as -
{x} = 20% of 125000
{x} = 20/100 x 125000
{x} = 20 x 1250
{x} = 25000
Therefore, the correct options are -
The proportion that represents the down payment is : 20/100 x 125000.The down payment is $25,000To solve more questions on functions & equations, visit the link-
https://brainly.com/question/29014197
#SPJ9
Find the equation of the line that contains the point (4, - 2) and is perpendicular to the line y = - 2x + 5.
Answers
y=1/2x
Solution:The slopes of perpendicular lines are opposite reciprocals of each other.The simplest way to determine a number's reciprocal is to flip it over, like so:\(-2 ~ - > -\displaystyle\frac{1}{2}\)Now, change the sign:\(\displaystyle\frac{1}{2}\)So we have the slope of the line that's perpendicular to the given line.Now, let's find the line's equation.First, let's write it in Point-Slope Form:y-y1=m(x-x1)y-(-2)=1/2(x-4) y+2=1/2x-2 (Point slope)Now, convert to slope-intercept:y=1/2x+2-2y=1/2xHope it helps.
Do comment if you have any query.
Answer:
y=1/2x
Step-by-step explanation:
"A waiter believes the distribution of his tips has a model that is slightly skewed to the left​, with a mean of ​$10.60 and a standard deviation of ​$6.60. He usually waits on about 50 parties over a weekend of work. ​a) Estimate the probability that he will earn at least ​$600. ​b) How much does he earn on the best 1​% of such​ weekends?"
Answers
Answer:
(a) 0.0668
(b) $638.74
Step-by-step explanation:
Let X denote the tips earned by a waiter.
It is provided that X follows a left-skewed distribution with mean, μ = $10.60 and standard deviation, σ = $6.60.
It is also provided that, the waiter usually waits on about n = 50 parties over a weekend of work.
According to the Central Limit Theorem if we have a population with mean μ and standard deviation σ and we take appropriately huge random samples (n ≥ 30) from the population with replacement, then the distribution of the sum of values of X, i.e ∑X, will be approximately normally distributed.
Then, the mean of the distribution of the sum of values of X is given by,
\(\mu_{S}=n\mu\\\)
And the standard deviation of the distribution of the sum of values of X is given by,
\(\sigma_{S}=\sqrt{n}\sigma\)
As the sample size is large, i.e. n = 50 > 30, the Central Limit Theorem can be used to approximate the sampling distribution of total tips by the normal distribution.
The mean and standard deviation are:
\(\mu_{S}=50\times 10.60=530\\\\\sigma_{S}=\sqrt{50}\times 6.60=46.67\)
(a)
Compute the probability that he will earn at least $600 as follows:
\(P(S\geq 600)=P(\frac{S-\mu_{S}}{\sigma_{S}}\geq \frac{600-530}{46.67})\\\\=P(Z>1.50)\\\\=1-P(Z<1.50)\\\\=1-0.93319\\\\=0.06681\\\\\approx 0.0668\)
Thus, the probability that he will earn at least $600 is 0.0668.
(b)
Let x represents his earnings on the best 1% of such weekends.
That is, P (X < x) = 0.99.
⇒ P (Z < z) = 0.99
The corresponding z-score is, 2.33.
Compute the value of x as follows:
\(z=\frac{S-\mu_{S}}{\sigma_{S}}\\\\2.33=\frac{x-530}{46.67}\\\\x=530+(2.33\times 46.67)\\\\x=638.7411\\\\x\approx 638.74\)
Thus, on the best 1% of such weekends the waiter earned $638.74.
Determine whether the table represents a linear or nonlinear function
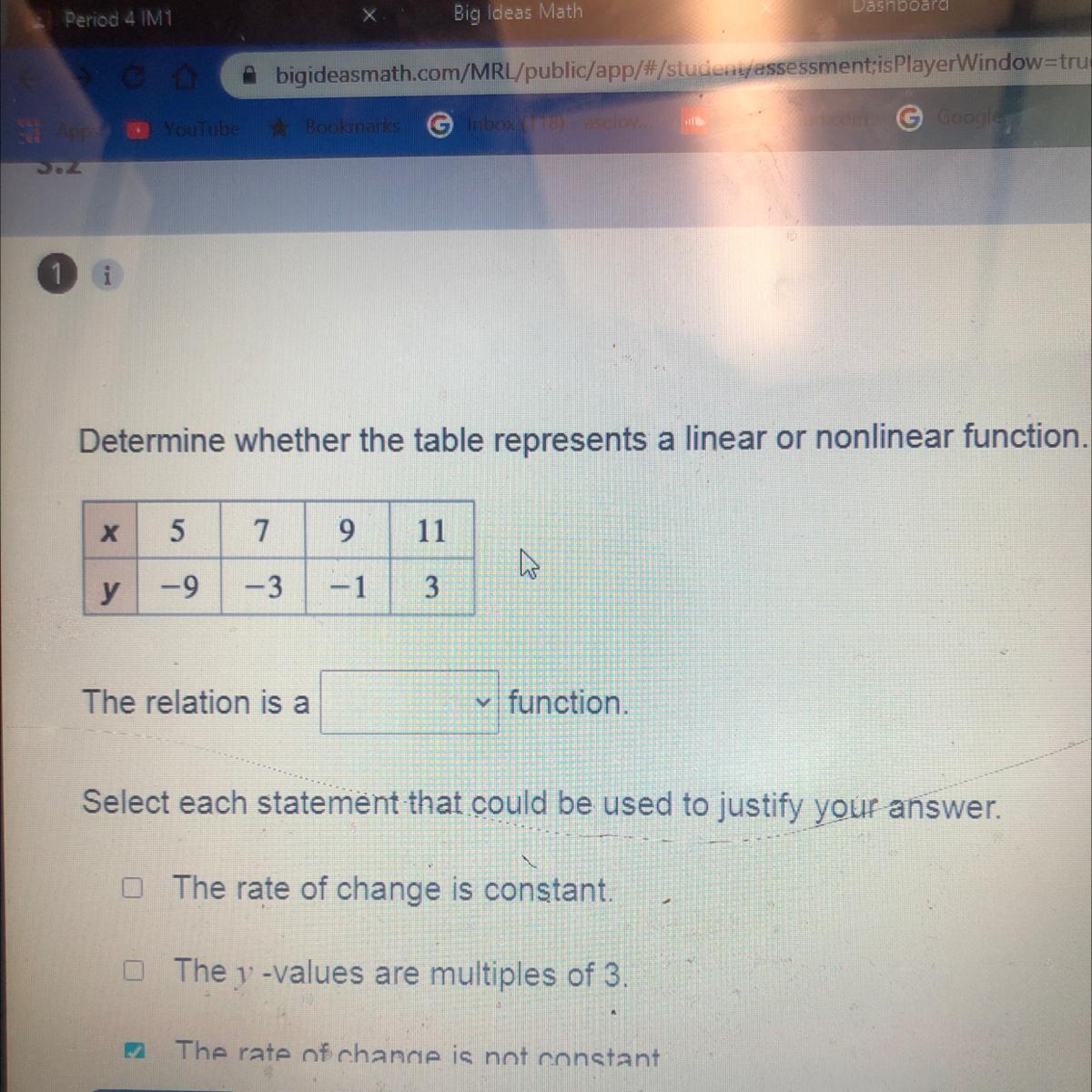
Answers
Answer:
nonlinear, as it isnt consistent may be wrong
Step-by-step explanation:
Answer:
It is a function, but it is nonlinear
Step-by-step explanation:
Every input is compared with exactly one output.
Samuel runs around a 1-mile track in 10 minutes, and Sophia runs around the same track in
10 minutes. Assuming they continue running at their respective speeds, how many total
miles will they run in 35 minutes? Express your answer as a mixed number.
Answers
Answer:
3.5 miles
Step-by-step explanation:
Step one:
given data
Samuel runs around a 1-mile track in 10 minutes
Samuel's speed is
speed= distance/time
speed= 1/10= 0.1 miles per minute
Sophia runs around the same track in 10 minutes
Hence Sophia's speed is also = 0.1 miles per minute
Step two:
Given that the time is 35 minutes, and their speeds are 0.1 miles per minute, we can find the distance from
speed= distance/time
distance= speed*time
distance= 0.1*35
distance= 3.5 miles
A kites string is fastened to the ground. the string is 324ft long and makes an angle of 68 degrees with the ground. A model of this is shown below. use the law of sites (sin A/a=sin B/b) to determine how many feet the kite is above the ground (x). Enter the value, rounded to the nearest foot. (PLEASE)

Answers
Answer:
x = 300 feet
Step-by-step explanation:
In the given right triangle,
Length of the string of the kite = 324 feet
Angle between the string and the ground = 68°
By applying law of Sines in the given right triangle,
\(\frac{\text{SinA}}{a}=\frac{\text{SinB}}{b}=\frac{\text{SinC}}{c}\)
Now we substitute the values of angles and sides in the formula,
\(\frac{\text{Sin68}}{x}=\frac{\text{Sin90}}{324}\)
\(\frac{\text{Sin68}}{x}=\frac{1}{324}\)
x = 324 × Sin(68)°
x = 300.41 feet
x ≈ 300 feet
Therefore, measure of side x = 300 feet will be the answer.
3. What is the value of x

Answers
Answer:
10
Step-by-step explanation:
using HYPOTHENUS theorem
8^2 + 6^2 = x^2
64 + 36= 100
√100=10
Answer:
10
Step-by-step explanation:
pythagros theorem
8 time 8 is 64
and
6 time 6 is 36
add them up we have
100
square root of 100 is 10
so the answer is 10
ur. welcome
Find sinθ, where θ is the angle shown.Give an exact value, not a decimal approximation.sinθ=
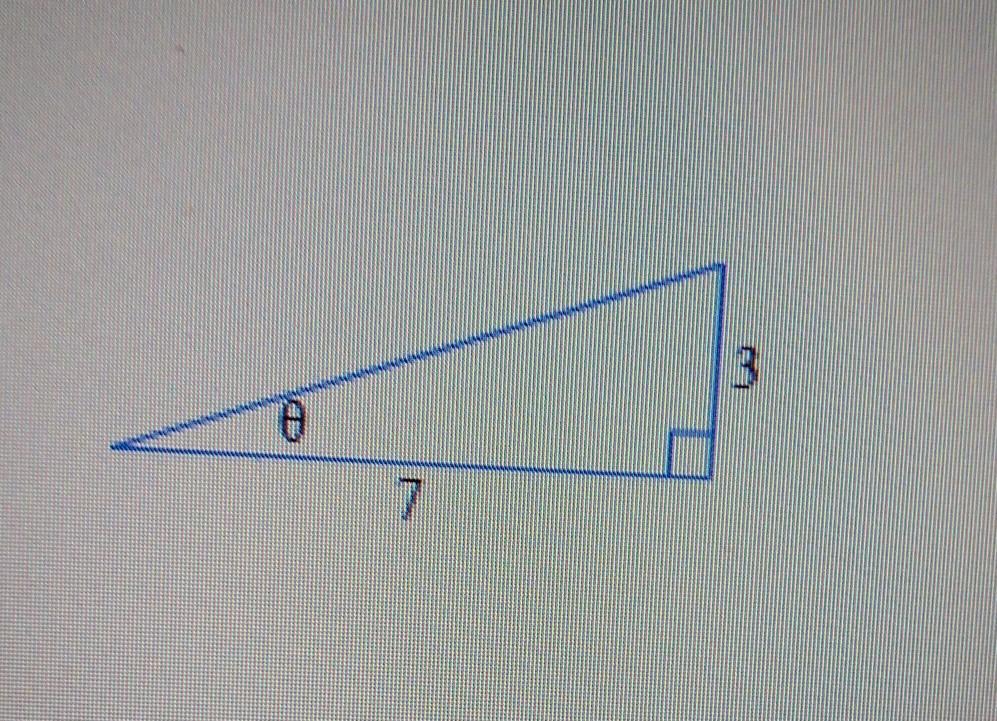
Answers
sin 0 = opposite side / hypotenuse
From the triangle:
opposite side = 3
adjacent side = 7
hypotenuse = ?
1.- Calculate the hypotenuse
h^2 = 7^2 + 3^2
h^2 = 49 + 9
h^2 = 58
h = squared root (58)
2.- Calculate the sin 0
sin = 3/squared root (58) =3squared root (58) / 58
\(\text{ sin }\emptyset\text{ = }\frac{3\sqrt[]{58}}{58}\)Help with this, thank you

Answers
The slope of a line perpendicular to the line whose equation is x - 2y = -8 is -2.
What are perpendicular lines?In Mathematics and Geometry, perpendicular lines are two (2) lines that intersect or meet each other at an angle of 90° (right angles).
From the information provided above, the slope for the equation of line m is given by:
x - 2y = -8
2y = x + 8
y = x/2 + 4
slope (m) of line m = 1/2
In Mathematics and Geometry, a condition that is true for two lines to be perpendicular is given by:
m₁ × m₂ = -1
1/2 × m₂ = -1
m₂ = -2
Slope, m₂ of perpendicular line = -2
Read more on perpendicular line here: brainly.com/question/27257668
#SPJ1
A company is considering to choose between two investment projects with the
following details.
Project A : Costs RM7 million in upfront costs and will generate RM3 million in
annual income for five years starting three years from now.
Project B : Costs RM2.5 million upfront and RM2 million in each of the next
three years. This project generates no annual income but will be sold
six years from now for a sales price of RM16 million.
By using Net Present Value approach, with a discount rate of 8%, determine
which project should be choosen by the company.
Answers
Answer: Project A should be chosen as it has the highest NPV.
Step-by-step explanation:
Project A
Present value of inflows:
First find the present value of inflows 3 years from today. Bear in mind that the inflow is constant so this is an annuity:
= 3 million * Present value interest factor of annuity, 8%, 5 years
= 3 million * 3.9927
= RM11,978,100
Discount this value to the present:
= 11,978,100 / (1 + 8%)³
= RM9,508,602
Net Present value = Present value of inflows - Investment
= 9,508,601 - 7,000,000
= RM2,508,601
Project B:
Find present value of costs:
= 2,500,000 + (2 million * Present value interest factor of annuity, 3 years, 8%)
= 2,500,000 + (2,000,000 * 2.5771)
= 2,500,000 + 5,154,200
= RM7,654,200
Net present value = (16,000,000 / (1 + 8%)⁶) - 7,654,200
= RM2,428,514
Project A should be chosen as it has the highest NPV.

Help with the following equation 8x²-6x-5=x
Answers
Answer:
\(8 {x}^{2} - 6x - 5 = x\)
\(8 {x}^{2} - 7x - 5 = 0\)
x = (7 + √((-7)^2 - 4(8)(-5)))/(2×8)
= (7 + √(49 + 160))/16
= (7 + √209)/16
= -.4661, 1.3411 (to 4 decimal places)
How can you use the data to understand what happened during the day?