The function f(x) is shown on the graph. The graph shows a downward opening parabola with a vertex at 3 comma 25, a point at negative 2 comma 0, a point at 8 comma 0, a point at 0 comma 16, and a point at 6 comma 16. What is the standard form of the equation of f(x)?
Answers
The equation of the parabola in standard form is f(x) = -(x - 3)² + 25
the vertex of the parabola is given as (3, 25), we know that the equation of the parabola can be written in vertex form as:
f(x) = a(x - 3)² + 25
where a is a constant that determines the shape of the parabola.
The point (6, 16) lies on the parabola
so we can substitute x = 6 and y = 16 into the equation above to find 'a'.
16 = a(6 - 3)² + 25
-9 = 9a
Dividing both sides by 9, we get:
a = -1
Now we know that the equation of the parabola is:
f(x) = -(x - 3)² + 25
Hence, the equation of the parabola in standard form is f(x) = -(x - 3)² + 25
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ1
Related Questions
The volume of a solid hemisphere is 1152π cm 3 . Find its curved surface area.
Answers
The curved surface area of the hemisphere is 864π cm².
What is a hemisphere?When a sphere is cut into two equal parts a hemisphere is formed.
The volume of a hemisphere is (2/3)πr³ and the area surface area of a hemisphere is 2πr².
Given, The volume of a solid hemisphere is 1152π cm³.
Therefore, (2/3)πr³ = 1152π.
r³ = 1728.
Now, 2×2×2 = 8 so 12³ is 1728.
r = 12 cm.
Now, The surface area is 2×π×144 cm².
= 864π cm².
If a circle is cut into two equal parts we call them each a semicircle.
learn more about hemispheres here :
https://brainly.com/question/12169868
#SPJ9
which of the following shows a proportional relationship

Answers
Answer:
h
Step-by-step explanation:
9514 1404 393
Answer:
c) H
Step-by-step explanation:
Consider the ratios of y to x:
F: 4/2 ≠ 13/5
G: 1/2 ≠ -2/5
H: 10/2 = 25/5 = 30/6 = 50/10 . . . . a proportional relationship
J: 3/2 ≠ 6/5
Table H shows a proportional relationship.
Solve the given system of differential equations by systematic elimination. 2 dx/dt- 6x + dy/dt = e^t
dx/dt - x + dy/dt = 7e^t
Answers
the given system of differential equations is: provide:
\(x = (6/4) * e^{(2t)} + C * e^{(5t)}\)
To solve the given system of differential equations by systematic elimination, we'll eliminate one variable at a time until we obtain a single equation in one variable.
The given system of differential equations is:
(1) \(2(dx/dt) - 6x + (dy/dt) = e^t\)
(2)\((dx/dt) - x + (dy/dt) = 7e^t\)
To eliminate dx/dt from the equations, we'll subtract equation (2) from equation (1):
\(2(dx/dt) - (dx/dt) - 6x + x + (dy/dt) - (dy/dt) = e^t - 7e^t\)
Simplifying, we have:
\((dx/dt) - 5x = -6e^t\)
Now, we have a single equation in one variable (x):
\((dx/dt) - 5x = -6e^t\)
To solve this linear first-order ordinary differential equation, we'll use an integrating factor. Let's denote the integrating factor as μ(t):
μ(t) = \(e^{\int ( -5dt)} = e^{(-5t)}\\\)
Multiplying the entire equation by μ(t), we have:
\(e^{(-5t)} * (dx/dt) - 5e^{(-5t)} * x = -6e^{(-5t)} * e^t\)
Applying the product rule, we can rewrite the left side of the equation as:
\((d/dt)[e^{(-5t)} * x] = -6e^{(-4t)}\)
Integrating both sides with respect to t, we obtain:
\(e^{(-5t)} * x = 6/4 * e^{(-4t)} + C\)
where C is the constant of integration.
Finally, solving for x, we have:
\(x = (6/4) * e^{(t)} * e^t + C * e^{(5t)}\)
Therefore, the solution to the given system of differential equations is:
\(x = (6/4) * e^{(2t)} + C * e^{(5t)}\)
to known more about contrapositive visit:
brainly.com/question/31383100
#SPJ11
Rewrite equation for the vertical and horizontal line passing through the point (-5,0)

Answers
we have the point
(-5,0)
so
Vertical Line ---------> x=-5
Horizontal line ----> y=0
Miki has 104 nickels and 88 dimes. She wants to divide her coins into groups where each group has the same number of
nickels and the same number of dimes. What is the largest number of groups she can have?
O 13
O 11
O 8
O 4
Answers
Answer:Eight i believe
Step-by-step explanation:
These marbles are placed in a bag and two of them are randomly drawn what is the probability of drawing two blue marbles if the first one is placed back in
Answers
Answer:
2/9
Step-by-step explanation:
larry wants new carpeting for rectangular living room. Her living room is 18 feet by 12 feet. How much carpeting does she need?
Answers
\(\text{To get the total surface area, all we have to do is multiply } 18 \text{ by } 12, \text{which gets us}\)\($18\cdot12 = \boxed{216\text{ ft}^2}\).
\(\text{So, our answer is } \boxed{216\text{ ft}^2}.\)
Larry needs 216 square feet of carpeting for her rectangular living room.
To find the amount of carpeting Larry needs, we need to calculate the area of her rectangular living room. The area of a rectangle can be found by multiplying its length by its width. In this case, the length of the living room is 18 feet and the width is 12 feet.
So, the area of the living room is:
Area = Length * Width
Area = 18 feet * 12 feet
Area = 216 square feet
Therefore, Larry needs 216 square feet of carpeting for her living room.
Learn more:About carpeting here:
https://brainly.com/question/18297841
#SPJ11
Assignment due tomorrow

Answers
The walk back to the school was 0.31 miles shorter than the walk to Grant's house.
What is the Pythagorean Theorem?The Pythagorean Theorem states that for a right triangle, the length of the hypotenuse squared is equals to the sum of the squared lengths of the sides of the triangle.
For this problem, we have a right triangle with sides 0.8 and 0.4, hence the length of the walk to the school is the hypotenuse given as follows:
h² = 0.8² + 0.4²
h = sqrt(0.8² + 0.4²)
h = 0.89 miles.
The length of the walk to Grant's house is given as follows:
0.4 + 0.8 = 1.2 miles.
Hence the difference is given as follows:
1.2 - 0.89 = 0.31 miles.
More can be learned about the Pythagorean Theorem at brainly.com/question/30203256
#SPJ1
Solve the 1 st order linear DEQ for x in (0,[infinity]). dy/dx + 2/x y=x
Answers
The solution to the first-order linear differential equation dy/dx + (2/x)y = x, where x is in the interval (0, ∞), is given by y = (C/\(x^{2}\)) + (x/3), where C is an arbitrary constant.
To solve the given differential equation, we'll use the method of integrating factors. First, we rewrite the equation in standard form by dividing both sides by x:
dy/dx + (2/x)y = 1.
The integrating factor is determined by multiplying both sides of the equation by the exponential of the integral of the coefficient of y, which in this case is (2/x):
I.F. =\(e^(\int(2/x)dx)\) = \(e^{(2ln|x|)}\) =\(e^{(ln|x^2|)}\) = \(x^{2}\).
Multiplying both sides of the equation by the integrating factor, we have:
\(x^{2}\)(dy/dx) + 2xy = \(x^3\).
Notice that the left-hand side can be expressed as the derivative of the product\(x^2\)y with respect to x. Applying the product rule, we get:
d/dx(\(x^{2}\)y) = \(x^3\).
Integrating both sides with respect to x, we obtain:
\(x^{2}\)y = (1/4)\(x^4\) + C,
where C is the constant of integration. Dividing through by \(x^{2}\), we get:
y = (1/4)\(x^{2}\) + C/\(x^{2}\).
Since x is in the interval (0, ∞), the term C/\(x^{2}\) approaches zero as x approaches infinity, resulting in the final solution:
y = (1/4)\(x^{2}\)+ (C/\(x^{2}\)).
To satisfy the initial condition, we need to determine the value of the constant C.
Learn more about first-order linear differential equation here:
https://brainly.com/question/32514979
#SPJ11
the distribution for the size of families in one u.s. city is shown below. size proportion 2 0.422 3 0.234 4 0.205 5 0.088 6 0.032 7 0.019 a family is selected at random. find the probability that the size of the family is at least 3.
Answers
0.578. is the probability that the size of the family is at least 3.
What does the math term "probability" mean?
The simple definition of probability is the likelihood that something will occur. We can discuss the probabilities of various outcomes, or how likely they are, whenever we are unsure of how an event will turn out.
Statistics describes the examination of events subject to probability.
P(X>=3) can be written as
= 1 - P(X<3)
= P(X<=2)
= 1-0.422
= 0.578
Learn more about Probability
brainly.com/question/11234923
#SPJ4
4, 6, 9, ... find the 7th term.
Answers
Answer:
16
Step-by-step explanation:
Here,
a=4
d= t1 - t2
=6-4
=2
tn = a +(n-1)d
t7 = 4+ (7-1)2
= 4+ 6×2
= 4 + 12
= 16
For which x is f(x)=–3?
–7
–4
4
5
Answers
What is the geometric means between 5 and 125?.
Answers
The geometric mean between 5 and 125 will be 25.
What is geometric mean?
The sequence where each word is varied by another by a common ratio is known as a geometric progression or geometric sequence. When we add a constant (which is not zero) to the term before it, the sequence's subsequent term is created. The following symbols stand in for it: a, ar, ar2, ar3, ar4, etc.
The Geometric Mean (GM) is the average value or mean that, in mathematics, represents the centre tendency of a group of numbers by calculating the product of their values. In essence, we multiply the numbers collectively and take the nth root of the resulting multiplied numbers, where n is the total number of data values.
The given number is 5, 125.
So the Geometric Mean willl be (5*125)\(.^{1/2}\)
So \((625)^{1/2}\)
= 25
Hence, the geometric mean between 5 and 125 will be 25.
Learn more about the geometric sequence, by the following link
https://brainly.com/question/24643676
#SPJ4
We expect most of the data in a data set to fall within 2 standard deviations of the mean of the data set. True False
Answers
True. We expect most of the data in a data set to fall within 2 standard deviations of the mean of the data set.
In a normal distribution, which is a common assumption for many data sets, it is expected that approximately 68% of the data falls within 1 standard deviation of the mean, and approximately 95% falls within 2 standard deviations of the mean. This is known as the empirical rule or the 68-95-99.7 rule.
The empirical rule is based on the properties of a normal distribution, which is symmetric and bell-shaped. It states that the majority of the data is concentrated around the mean, with the spread of the data increasing as we move further away from the mean. Within 2 standard deviations of the mean, we capture a large portion of the data, approximately 95%. This means that most of the data points are expected to fall within this range.
However, it's important to note that this statement assumes a normal distribution and may not hold true for all data sets. In cases where the data does not follow a normal distribution or has outliers, the proportion of data falling within 2 standard deviations may differ.
Learn more about empirical rule here:
https://brainly.com/question/30573266
#SPJ11
my head is empty for now, i rly can't with online classes
so anyone wanna help me?
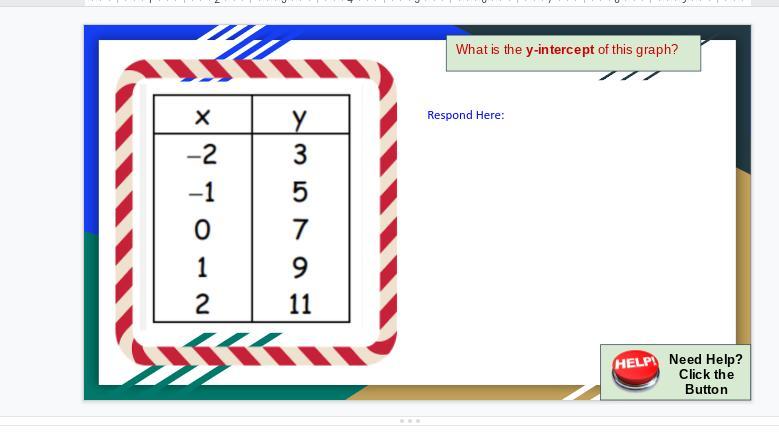
Answers
Answer:
The Y intercept is (0,7)
Step-by-step explanation:
If it is a y intercept, there will be a number in the y coordinate. For example, (x,y) if the point said (7,0) that would be the x intercept. Because it it (0,7) and in the y place that makes it a y intercept. I hope this helped :)
3.8 repeating as a fraction or mixed number in simplist form
Answers
When unwrapped, the lateral surface area of cone A is a sector with central angle 6 radians and radius pi. What is the length of the radius of cone A
Answers
The length of the radius of cone A. is \(\frac{\pi}{6}\).
The lateral surface area of cone A is a sector with central angle 6 radians and radius π.
We can use the formula for sector area to find the lateral surface area of the cone.
Area of sector = θ/2π×π²
where θ is the central angle and π is the radius.
Area of cone’s lateral surface area (L) =θ/2π×2πr=rθ.
So, r = L/θ = π/6 (when L=π and θ=6 radians).
The length of the radius of cone A is π/6 which is approximately 0.524.
Therefore, the length of the radius of cone A is \(\frac{\pi}{6}\), when unwrapped, given that the lateral surface area of cone A is a sector with central angle 6 radians and radius pi.
Learn more about cone here:
brainly.com/question/23877107
#SPJ12
The weights of 6-week-old poults (juvenile turkeys) are normally distributed with a mean 9.0 pounds and standard deviation 2.4 pounds. A turkey farmer wants to provide a money-back guarantee that her 6-week poults will weigh at least a certain amount. What weight should she guarantee so that she will have to give her customer's money back only 1% of the time
Answers
The turkey farmer should guarantee a weight of approximately 4.57 pounds to have to give her customers' money back only 1% of the time.
To determine the weight that the turkey farmer should guarantee, we need to find the value that corresponds to the 1st percentile of the weight distribution. This value represents the weight below which only 1% of the poults' weights would fall.
To find the 1st percentile, we can use the z-score formula: z = (x - μ) / σ, where x is the value, μ is the mean, and σ is the standard deviation. We want to find the value of x that corresponds to a z-score of -2.33, which corresponds to the 1st percentile in a standard normal distribution.
Rearranging the formula, we have x = z * σ + μ. Plugging in the values, we get x = -2.33 * 2.4 + 9.0 ≈ 4.57 pounds.
Therefore, the turkey farmer should guarantee a weight of approximately 4.57 pounds to have to give her customers' money back only 1% of the time. This ensures that the majority of the poults' weights will exceed the guaranteed weight, satisfying the money-back guarantee condition.
Learn more about approximately here
https://brainly.com/question/29669607
#SPJ11
Can someone pleasee help I’ll mark brainlist!!!

Answers
Answer:4/C
Step-by-step explanation:
Answer:
2.4
It is the 1st one
Step-by-step explanation:
There are 60 min in 1 hour so divide 60/20min = 3
Then multiply 4/5*3 = 2.4
HOpe this helps
Find the derivative of the function using the definition of derivative. g(t) = 3 t
Answers
The derivative of the function using the definition of derivative is 3.
The given function is g(t) = 3t.
We have to find the derivative of the function using the definition of derivative.
We know that,
Definition of derivative:-
The derivative of a function is the rate of change of the function's output relative to its input value.
Here,
Input value = t
Output value = g(t)
Given y = g(t), the derivative of g(t), denoted g'(t) (or dg(t)/dt), is defined by the following limit:
\(g'(t)= \lim_{h \to 0} \frac{g(t+h)-g(t)}{h}\)
We have the function:-
g(t) = 3t
Hence, according to the data given in the question, we can write,
g'(t) =
\(\lim_{h \to 0} \frac{g(t+h)-g(t)}{h} \\\\ \lim_{h \to 0} \frac{3(t+h)-3(t)}{h}\\\\ \lim_{h \to 0} \frac{3t+3h-3t}{h}\\\\ \lim_{h \to 0} \frac{3h}{h}\\\\\lim_{h \to 0} 3\)
g'(t) = 3
To learn more about derivative of the function, here:-
https://brainly.com/question/28104078
#SPJ4
Which function is it

Answers
Answer:
The second answer
Step-by-step explanation:
The y is all by itself in ANY problem so the number all by itself is where the dot should be in this case 3
5.) g(x) = -4x + 2. Find x when g(x) = 22.
I'm on a timed test and I wasn't able to study because of personal reasons
Answers
Answer:
x = -5
Step-by-step explanation:
If g(x) = 22 and g(x) = -4x + 2, then -4x + 2 = 22.
Isolate x.
-4x = 22 - 2
= -4x = 20
= x = 20 ÷ -4
= x = -5
how i do inequalities
Answers
Answer:
Following the steps given below you can solve any inequality.
Step-by-step explanation:
I will give an example and explain you step by step of solving an inequality.
Consider an inequality: \(2x+4 > 8\)
In this inequality we need to find the value of x.
Step 1: Write the inequality
\(2x+4 > 8\)
Step 2: Subtract 4 on both sides of inequality
\(2x-4 > 8-4\\2x>4\)
Step 3: Now, you have divide both sides by 2 to get value of 4
\(\frac{2x}{2}>\frac{4}{2}\\x>2\)
So, solving the inequality we find value of x: \(x>2\)
Following these steps you can solve any inequality.
I hope it will help you.
What is the equation of the line that passes through the point (2,−1) and has a slope of 3/2
Answers
y=3/2x -4
hope this helps:))
Given :-
A line having a slope of 3/2 passes through (2,-1) .
To Find :-
The equation of the line .
Answer :-
According to the question ,
m = 3/2
Point = (2,-1)
We know Point slope form of the line as ,
y - y¡ = m ( x - x ¡ )
Substitute ,
y - (-1) = 3/2 ( x - 2 )
y + 1 = 3/2x - 3/2*2
y +1 = 3/2x - 3
2( y +1) = 3/2x *2 - 3*2
2y + 2 = 3x - 6
3x -2y -8 = 0
If the 1t peron ave 1/4 of total , 2nd peron ave 2/3 of total and the 3rd peron ave 1/10 which fraction i left to pay for the birthday party
Answers
Although part of your question is missing, you might be referring to this full question: If the 1st person saves 1/4 of total, 2nd person saves 2/3 of total, and 3rd person saves 1/10, which fraction left to pay for the birthday party?
The fraction left to pay for the birthday party is 17/30.
The calculation is as follows:
1 * 1/4 = 1/4 … (1)
1/4 * 2/3 = 2/12 … (2)
2/12 * 1/10 = 2/120 … (3)
Fraction left to pay:
= 1 - (1/4 + 2/12 + 2/120)
= 1 - (30/120 + 20/120 + 2/120)
= 1 - (52/120)
= 1 - 13/30
= 30/30 - 13/30
= 17/30
Thus, the fraction left to pay for the birthday party is 17/30.
What is fraction?A fraction is a part of a whole. In arithmetic, the number is expressed as a quotient, where the numerator is divided by the denominator. In a simple fraction, both are integers. A complex fraction has a fraction in the numerator or denominator. In a proper fraction, the numerator is less than the denominator.
Learn more about fraction at: https://brainly.com/question/10354322
#SPJ4
we desire the residuals in our model to have which probability distribution? select answer from the options below normal binomial poisson
Answers
The distribution that the residuals in our model to follow is equals to the normal probability distribution. So, option(a).
Because residuals are defined as the difference between any data point and the regression line, they are sometimes called "errors". An error in this context does not mean that there is anything wrong with the analysis. In other words, the residual is the error that is not described by the regression line. The residue(s) can also be expressed by "e". The formula is written as, Residual = Observed value – predicted value or
\(e = y – \hat y \).
In order to draw valid conclusions from your regression, the regression residuals should follow a normal distribution. The residuals are simply the error terms or differences between the observed value of the dependent variable and the predicted value. Therefore, the residuals should have a normal distribution.
For more information about residuals, visit:
https://brainly.com/question/15404560
#SPJ4
Complete question:
we desire the residuals in our model to have which probability distribution? select answer from the options below
a) normal
b) binomial
c) poisson
you & three friends go to the twin carnival. you have a coupon for $20 off that will save your group money! if the total bill to get into the carnival was 100$ how much does one regular price ticket cost?

Answers
Answer:
$30
Step-by-step explanation:
100+ the twenty you got off is 120 and dvide 120/4=30 I am either making this way to easy or just dont understand lol
Sixteen blocks are needed to build a four-step double staircase like
the one on the right. How many blocks will be needed to build a
double staircase of similar shape with 50 steps?
Snacks:
Answers
x blocks = 50 steps
(16 blocks x 50 steps)/4 steps
= 200 blocks
evalute 7 to the power of negative 2
Answers
I took a quite about these
0.5+0.3-(-0.5--0.3) I AM SOOOO SRRY GUYS
Answers
Answer:
0.5+0.3-(-0.5-0.3)
=1.6