The first three terms of a sequence are given. Round to the nearest thousandth (if necessary): 261. 256, 251.... Find the 50th term.
Answers
Answer:
50th term = 16
Step-by-step explanation:
Related Questions
Alex feeds his cat ⅗ of a can of cat food a day how many cans of cat food should Alex buy each week
Answers
Answer:
5
Step-by-step explanation:
3/5 times 7 is 4 1/5 and you cant buy 1/5 of a can so you have to round up to 5
A customer service survey was conducted of 400 customers: 200 men and 200 women. The data on one of the questions show that 115 of the men and 165 of the women rate the customer service as excellent. What percentage of the men gave an excellent rating
Answers
For the customer service survey, the percentage of the men gave an excellent rating is 57.5%.
The percentage of the men who gave an excellent rating can be calculated by dividing the number of men who gave an excellent rating by the total number of men who took the survey and multiplying by 100%.
Total number of customers surveyed = 400 (200 men and 200 women)
Number of men who rated customer service as excellent = 115
Number of women who rated customer service as excellent = 165
To find percentage of the men who gave an excellent rating, formula to be used:
Percentage of the men who gave an excellent rating = (Number of men who rated customer service as excellent / Total number of men who took the survey) x 100%
Therefore,
Percentage of the men who gave an excellent rating = (115/200) x 100%
Percentage of the men who gave an excellent rating = 57.5%
Therefore, the answer is 57.5%.
Learn more about Percentage:
https://brainly.com/question/24877689
#SPJ11
Each of ten tickets is marked with a different number from 1 to 10 and put in a box. If you draw a ticket from the box, what is the probability than
you will draw a number greater than 3?
Answers
Answer:
the probability is 7
Step-by-step explanation:
if you think about it this way you have 10 tickets:
1 2 3 4 5 6 7 8 9 10
they say that if you pull anything greater than 3 so anything greater than 3 would be higher. 4, 5, 6, 7, 8, 9, 10 if you count from 4- 10 the answer is 7. I don't know if that helped at all but hopefully it did.
8th grade urgent math super easy please

Answers
Answer:
n> -6
Step-by-step explanation:
-35n -28< 182
+28 +28
______________
-35n < 210
n> -6
Can somebody plz answer both correct and just write which one I circle thanks!! (Only if u remember)
(WILL MARK BRAINLIEST) :D

Answers
Answer:
7. +6
8. -2
9. +1
10. +2
11. -4
12. +4
13. -3
14. -2
15. +1
16. -5
17. -5
18. 0
Step-by-step explanation:
Given 3,8,14,x+6,2x-3,25,32,50 are in ascending order , whose median is 18. Find the unknown terms.
Answers
What is ZT?
4x + 1
W
Х
2x
T
Z
Y
5x - 6
A 7
B. 14
C. 28
D. 29
Answers
Step-by-step explanation:
which one are you asking for???
HELP!!!!!BRAINLIEST
PLEASE SHOW YOUR WORK ON A PAPER BRAINLIEST!!!!!!!!!!!!!!!!!!

Answers
Answer: Noah's mixture would be more flavorful and fizzy because his ratio of water and fizz powder aren't to off (not a large ratio gap). Andre's orange fizz would be a little more watered down making it less fizzy and less flavorful because 8 cups were added instead of 6 or 7 cups of water. Also Noah would have less drink made them Andre because he only used 6 cups of water.
Step-by-step explanation:
5-6. Brianna is a technician at a radio station. She knows that, unlike many other types of waves,
radio waves can be very long. Below is the graph for a radio wave that is 1 meter in length.
Here is the function of the radio wave: f(x) = sin (21x)
Graph the function
Write down the amplitude, period, and frequency.
The amplitude is 1
The period is 2
The frequency is 1/2
Answers
Answer:
21.meters
Step-by-step explanation:
po sana makatulong
Fred is N years old. Michael is six years younger than Fred and two years older than Chris. What is the sum of the three ages?
Answers
Let's first determine Jim's age and Sam's age FOUR YEARS AGO
If 2x = Jim's age TODAY, then 2x - 4 = Jim's age FOUR YEARS AGO
If x - 2 = Sam's age TODAY, then x - 2 - 4 = Sam's age FOUR YEARS AGO
Four years ago Jim was 4 times as old as Sam.
In other words, the value of 2x - 4 is 4 times the value of x - 2 - 4
So, we can write: 2x - 4 = 4(x - 2 -4)
Simplify right side: 2x - 4 = 4(x - 6)
Expand right side: 2x - 4 = 4x - 24
Add 24 to both sides: 2x + 20 = 4x
Subtract 2x from both sides: 20 = 2x
Solve: x = 10
How old is Jim NOW?
2x = Jim's age TODAY
Since x = 10, we know that Jim's age = 2(10) = 20
Order each set of numbers from least to greatest. 41 3 2 9 0.6 3' V 16' 9.

Answers
9. 0.6, 2/3, Square root of 9/16
9/16,2/3,0.6
Find the length of the unknown side. Round your answer to the nearest whole number.
A. 7 inches
B. 10 inches
C. 25 inches
D. 50 inches

Answers
Answer:
d. 50
Step-by-step explanation:
5² + 5² = 50
I hope this helps!
Find the missing side of the triangle. Round your answers to the nearest tenth if necessary.
15.3 m
10 m
24.6 m
22.4 m

Answers
Answer:
Solution given:
perpendicular[p]=x
base[b]=11.6m
hypotenuse[h]=19.2m
by using Pythagoras law
h²=p²+b²
19.2²-11.6²=x²
x=\(\sqrt{234.08}\)
x=15.3m
option
a.
15.3 m
Answer:
15.3 m
Step-by-step explanation:
c refers to the longest side (hypotenuse) whereas a and b referes to the two other smaller sides of atriangle.
pythagoras theorem
a^2 + b^2 = c^2
11.6^2 + x^2 = 19.2^2
134.56 + x^2 = 368.64
x^2 = 368.64 - 134.56
x^2 = 234.08
x=\(\sqrt{234.08\)
x=15.29
x=15.3 m
Factor with the distributive pro
Apply the distributive property to factor out the greatest common factor.
32+44
Answers
The greatest common factor is 4.
Step-by-step explanation:
Describe the shape of the distribution.
A. It is symmetric.
B. It is uniform.
C. It is bimodal.
D. It is skewed.

Answers
A contractor is building a wheelchair ramp for a doorway that is 12 feet above the ground. To meet ADA guidelines, the ramp will make an angle of
with the ground to the nearest tenth of an inch, what is the length of the ramp? "hint-how many inches in a foot?"
The distance of AC is
B
4.8
inches
A
1.2 ft
B
Answers
The length of the ramp is approximately 14.3 inches.
We can use trigonometry to determine the length of the ramp. Let's name the ramp's length "x."
We know that the height of the doorway is 1.2 feet, and we want the ramp to make an angle of 4.8 degrees with the ground.
From trigonometry, we know that as per the tangent function,
tan(4.8) = opposite/adjacent
where "opposite" is the height of the doorway (1.2 feet) and "adjacent" is the length of the ramp (x).
Now we can solve for x:
tan(4.8 ) = 1.2 / x
x = 1.2 / tan(4.8 )
x ≈ 14.3 inches
To learn more about the tangent function;
https://brainly.com/question/22043858
#SPJ1
Factorise p²-10p+25
Answers
Answer:
Step-by-step explanation:
The expression p² - 10p + 25 can be factored as follows:
p² - 10p + 25 = (p - 5)²
This is an example of perfect square trinomial. It can be recognized as such because the first and last terms are perfect squares (p² and 25), and the middle term (-10p) is twice the product of the square roots of the first and last terms (2√(p²×25) = 2p×5 = 10p).
So, the factored form of the expression is (p - 5)².
Step-by-step explanation:
The answer to this question is (p-5)^2

Los primeros días de enero, el representante del mercado recibió cierta cantidad de di-
nero, hizo una operación y se dio cuenta que habían pagado 15 personas. ¿Cómo puede
saber la cantidad recibida?
15
425
Answers
El ejercicio completo con las opciones de respuesta está a continuación:
Los primeros días de enero el representante del mercado recibió cierta cantidad de dinero,hizo una operación y se dio cuenta que habían pagado 15 personas,cómo puede saber la cantidad recibida?
a.Multiplicando el dividendo por el divisor
b. Sumando el dividendo con el cociente y el residuo
c.Multiplicando el divisor por el cociente y sumando el residuo
d.Multiplicando el dividendo por el cociente y sumando el residuo
Answer:
La opción c es la respuesta correcta
Step-by-step explanation:
El valor de 15 corresponde al cociente es decir al total de personas que pagaron;el ejercicio nos da el valor del divisor que es 425 ; para saber cual es la cantidad exacta recibida debemos multiplicar el divisor por el cociente y si hay residuo sumarlo; el ejercicio nos queda de la siguiente manera:
425 x 15 = 6.375 (la cantidad recibida fue de 6.375)
\(\frac{6375}{425}\) = 15 (comprobación de la división para obtener el cociente con valor de 15)
does the confidence interval provide convincing evidence that the true mean volume is different than 12 ounces? explain your answer.
Answers
The convincing evidence provided by the confidence interval depends on whether the interval includes or excludes the value of 12 ounces. If it excludes 12 ounces, it provides convincing evidence of a difference. If it includes 12 ounces, it does not provide convincing evidence of a difference.
To determine whether the confidence interval provides convincing evidence that the true mean volume is different than 12 ounces, we need to examine the confidence interval and its relationship to the value of 12 ounces.
A confidence interval is constructed based on sample data and provides a range of values within which the true population parameter is estimated to lie. The width of the confidence interval is influenced by factors such as the sample size, variability of the data, and chosen level of confidence.
If the confidence interval for the mean volume does not include the value of 12 ounces, it suggests that the true mean volume is likely to be different from 12 ounces. In this case, the confidence interval provides convincing evidence that the true mean volume is different from 12 ounces.
However, if the confidence interval does include the value of 12 ounces, it does not provide convincing evidence that the true mean volume is different from 12 ounces. This suggests that the data is consistent with the possibility that the true mean volume could be 12 ounces.
To learn more about confidence interval: https://brainly.com/question/20309162
#SPJ11
PLEASE HELP I HAVE BEEN TRYING TO FIGURE THIS OUT FOR 4 HOURS AND 15 MINUTES





Answers
Answer:
1. C) 3
2. D) -1
3. D) 7^2 - 8*2 - 16
4. B) 75
5. B) 6^2 + (2 - 8)*sqrt(81)
Step-by-step explanation:
1. (10 - (6-4)^2)/2
= (10 - 2^2)/2
= (10 - 4)/2
= 6/2
= 3
2. PEMDAS states that Multiplication is before Subtraction
8 - (5^2-7)/2
= 8 - (25-7)/2
= 8 - 18/2
= 8 - 9
= -1
3. D) 7^2 - (8*2) - 16
= 49 - 16 - 16
= 49 - 32
= 17
4. 3(2 + 3)^2
= 3(5)^2
= 3(25)
= 75
5. 6^2 + (2 - 8)*sqrt(81)
= 36 + (-6*9)
= 36 - 54
= -18
Addison earned a score of 510 on Exam A that had a mean of 550 and a standarddeviation of 40. She is about to take Exam B that has a mean of 26 and a standarddeviation of 5. How well must Addison score on Exam B in order to do equivalentlywell as she did on Exam A? Assume that scores on each exam are normallydistributed

Answers
Exam A:
\(\begin{gathered} \text{Score (x)=510} \\ \mu\text{ (mean)=55}0 \\ \sigma\text{ (standard deviation)=40} \end{gathered}\)\(\begin{gathered} Z\text{ = }\frac{x\text{ -}\mu}{\sigma} \\ Z\text{ = }\frac{510-550}{40}=-1 \end{gathered}\)Z = -1, then...
Exam B:
\(\begin{gathered} x\text{ = ?} \\ \mu=26 \\ \sigma=5 \end{gathered}\)\(x=Z\times\sigma+\mu=-1\times5+26=21.00\)Answer: 21
If you already know |aN| and |v|, then the formula aN=k|v|2 gives a convenient way to find the curvature. Use it to find the curvature and radius of curvature of the curve jr(t) = (cos t + t sin t) i + (sin t - t cos t) j?, t > 0.
Answers
The curvature of the curve is k(t) = 1/(1+t2)^(3/2) and the radius of curvature is R(t) = (1+t^2)^(3/2).
To find the curvature and radius of curvature of the curve, we need to find the components of the unit tangent vector T(t) and the normal vector N(t) at a given point. Then we can find the curvature as the magnitude of the rate of change of the unit tangent vector with respect to arc length, which is given by |dT/ds|. The radius of curvature is the reciprocal of the curvature.
First, we find the unit tangent vector T(t) by differentiating r(t) with respect to t and dividing by its magnitude:
r(t) = (cos t + t sin t) i + (sin t - t cos t) j
v(t) = dr/dt = (-sin t + t cos t) i + (cos t + t sin t) j
|v(t)| = sqrt[(-sin t + t cos t)^2 + (cos t + t sin t)^2]
= sqrt[1 + t^2]
Therefore, the unit tangent vector is:
T(t) = v(t) / |v(t)| = (-sin t + t cos t) / sqrt[1 + t^2] i
+ (cos t + t sin t) / sqrt[1 + t^2] j
Next, we find the normal vector N(t) by differentiating T(t) with respect to arc length s and dividing by its magnitude:
dT/ds = |v(t)| dT/dt
N(t) = (1 / |dT/ds|) dT/ds
We have:
dT/dt = (-cos t - t sin t) / (1 + t^2)^(3/2) i
+ (-sin t + t cos t) / (1 + t^2)^(3/2) j
|dT/ds| = |v(t)| / |r'(t)| = sqrt[1 + t^2] / sqrt[(cos t + t sin t)^2 + (sin t - t cos t)^2]
= sqrt[1 + t^2] / sqrt[1 + t^2]
= 1
Therefore, the normal vector is:
N(t) = (-cos t - t sin t) / sqrt[1 + t^2] i
+ (-sin t + t cos t) / sqrt[1 + t^2] j
The curvature is given by:
k = |dT/ds|
We have:
dT/ds = |v(t)| dT/dt = (1 + t^2) (-cos t - t sin t) / (1 + t^2)^(3/2) i
+ (1 + t^2) (-sin t + t cos t) / (1 + t^2)^(3/2) j
= (-cos t - t sin t) / (1 + t^2)^(1/2) i
- (sin t - t cos t) / (1 + t^2)^(1/2) j
Therefore, the curvature is:
k = |dT/ds| = sqrt[(-cos t - t sin t)^2 + (sin t - t cos t)^2] / (1 + t^2)
= sqrt[2] / (1 + t^2)
The radius of curvature is the reciprocal of the curvature:
R = 1 / k = (1 + t^2) / sqrt[2]
To find the curvature and radius of curvature at t = 1, we substitute t = 1 into the expressions for k and R:
k = sqrt[2] / 2
R = (1+t^2)^(3/2)
To know more about curvature,
https://brainly.com/question/31503631
#SPJ11
What is the solution to this system of equations?

Answers
Step-by-step explanation:
the solution is the crossing point (where both equations deliver the same result).
and that is (2, 2).
Molly Hamilton deposited $50,000 at Bank of America at 8% interest compounded quarterly. What is the effective rate (APY) to the nearest hundredth percent?
Answers
The effective rate (APY) for Molly's deposit at Bank of America is approximately 8.24%.
To calculate the effective rate or annual percentage yield (APY) for Molly Hamilton's deposit of $50,000 at Bank of America with an interest rate of 8% compounded quarterly, we use the formula APY = (1 + (r/n))^n - 1, where r is the annual interest rate and n is the number of compounding periods per year.
In this case, the annual interest rate is 8% or 0.08, and since interest is compounded quarterly, there are 4 compounding periods per year. Plugging in these values into the APY formula, we have APY = (1 + (0.08/4))^4 - 1.
Evaluating the expression, we find APY ≈ 0.0824 or 8.24%. Therefore, the effective rate (APY) for Molly's deposit at Bank of America is approximately 8.24%, rounded to the nearest hundredth percent.
To learn more about “ interest” refer to the https://brainly.com/question/25720319
#SPJ11
Solve using the quadratic formula. Show all work. Write each solution in simplest form. No decimals.
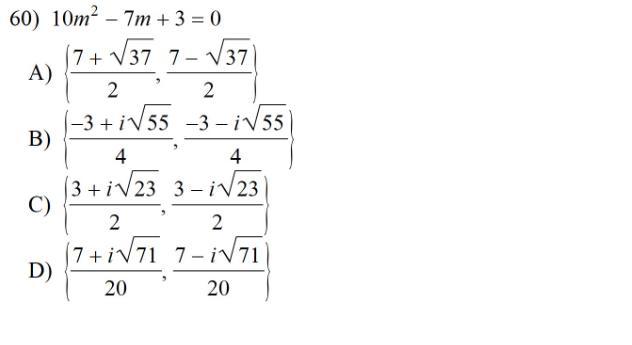
Answers
Given:
The quadratic equation is:
\(10m^2-7m+3=0\)
To find:
The solutions for the given equation by using the quadratic formula.
Solution:
If a quadratic equation is \(ax^2+bx+c=0\), then the quadratic formula is:
\(x=\dfrac{-b\pm \sqrt{b^2-4ac}}{2a}\)
We have,
\(10m^2-7m+3=0\)
Here, \(a=10,b=-7,c=3\). Using the quadratic formula, we get
\(m=\dfrac{-(-7)\pm \sqrt{(-7)^2-4(10)(3)}}{2(10)}\)
\(m=\dfrac{7\pm \sqrt{49-120}}{20}\)
\(m=\dfrac{7\pm \sqrt{-71}}{20}\)
\(m=\dfrac{7\pm i\sqrt{71}}{20}\) \([\because \sqrt{-a}=i\sqrt{a},a>0]\)
Therefore, the solution set of the given equation is \(\left\{\dfrac{7- i\sqrt{71}}{20},\dfrac{7+ i\sqrt{71}}{20}\right\}\). Hence, the correct option is D.
What is the end behavior of the function f of x equals 3 times the cube root of x?
As x → –∞, f(x) → –∞, and as x → ∞, f(x) → ∞.
As x → –∞, f(x) → ∞, and as x → ∞, f(x) → –∞.
As x → –∞, f(x) → 0, and as x → ∞, f(x) → 0.
As x → 0, f(x) → –∞, and as x → ∞, f(x) → 0.
Answers
The end behavior of \(f\left(x\right)\ =3\sqrt[3]{x}\) is how its value changes as x changes
The end behavior of the function is \(\mathrm{as}\:x\to \:+\infty \:,\:f\left(x\right)\to \:+\infty \:,\:\:\mathrm{and\:as}\:x\to \:-\infty \:,\:f\left(x\right)\to \:+\infty \:\)
How to determine the end behavior?The function is given as:
\(f\left(x\right)\ =3\sqrt[3]{x}\)
The above function is a cube root function.
A cube root function has the following properties:
As x increases, the function values increasesAs x decreases, the function values decreasesThis means that the end behavior of the function is:
\(\mathrm{as}\:x\to \:+\infty \:,\:f\left(x\right)\to \:+\infty \:,\:\:\mathrm{and\:as}\:x\to \:-\infty \:,\:f\left(x\right)\to \:+\infty \:\)
Read more about function end behaviors at:
https://brainly.com/question/1365136
Answer:
The answer is A
Step-by-step explanation:
Had taken the test
Write an equivalent expression to
(x+7)+3y
Answers
Answer:
2x+14+6y
Step-by-step explanation:
Can someone please help me

Answers
Answer:
I think it would be the last one
find a attached the question

Answers
Answer:
Using distance formula :
AB = \(\displaystyle \sqrt{(10-1)^2 + (3 - 7)^2}\)
AB = \(\sqrt{81 + 16}\)
AB = 9.85 units
find f'(x) when f(x) = (x^2) - 2x. find the equation of the tangent line and the normal line at x=4
Answers
The derivate of a function f(x) is determinated as:
\(f^{\prime}(x)=\lim _{h\to0}\frac{f(x+h)-f(x)}{h}\)For the function
\(f(x)=x^2-2x\)First we have to determine de f ( x + h ) as follow:
\(f(x+h)=(x+h)^2-2(x+h)\)\(f(x+h)=x^2+2xh+h^2-2x-h^{}\)Then we calculate and simplify the coeficient in the first formula
\(\frac{f(x+h)-f(x)}{h}\)\(\frac{(x^2+2xh+h^2-2x-h^{})-(x^2-2x)}{h}\)\(\frac{x^2+2xh+h^2-2x-h^{}-x^2+2x}{h}=\frac{h^2+2xh-h}{h}\)\(\frac{h^2+2xh-h}{h}\text{ = }\frac{h(h+2x-1)}{h}=h+2x-1\)So the derivate is:\(f^{\prime}(x)=\lim _{h\to0}\frac{f(x+h)-f(x)}{h}=\lim _{h\to0}h+2x-1\)\(f^{\prime}(x)=0+2x-1\)\(f^{\prime}(x)=2x-1\)------------------------------------------------------------------------------------The equation of the tangent:
First you need to know that the derivate of a function is equal to the slope (m) of the tangent of this function
And the equation to thist tangent in a specific point will be find using the next formula:
\(y-f(x_0)=m(x-x_0)_{}\)We have to calculate the slope in the point x =4 using the derivate:
\(m=2x-1\)\(m=2(4)-1=7\)In the point x=4
Calculate the value of f(x0) substituting in the function the given point x:
\(f(4)=4^2-2(4)\text{ = }8\)Knowing that we put the value of m and f(x0) in the equation of the tangent:
\(y-8=7(x-4)_{}\)\(y-8=7x-28\)\(y=7x-28+8\)So the equation of the tangent in x= 4 is:\(y=7x-20\)---------------------------------------------------------------------------
The normal line
The slope of the normal line is the opposite of the slope of theu tangent in an espesific point:
\(m_n=-\frac{1}{m_t}\)So in this situation is:
\(m_n=-\frac{1}{7}\)The equation of the normal line is given by the next formula:
\(y-f(x_0)=m_n(x-x_0)_{}\)Replacing the data we obtain:
\(y-8=-\frac{1}{7}(x-4)_{}\)\(y-8=-\frac{1}{7}x+\frac{4}{7}\)So the equation of the normal line is:\(y=-\frac{1}{7}x+\frac{60}{7}\)