The data for the height and weight of different people was collected the line of best fit for this date it was determined to be Y equals 0. 9 1X -65. 5 where X is the height in centimeters and why is the weight in kilograms is in the equation predict the height of a person who weighs 63 kg

Answer:

1- a²+b²=c²

2- 5²+12²=13²

3- 25+144=169

4- 169=169

Answer:

f(x-2)

Step-by-step explanation:

This is because f(x)-2 or f(x)+2 is moving it up or down and f(x+2) seems like it would be the right answer but it is reversed when it's in parenthesis so it would actually be moving 2 to the left.

Answer:

its f (x-2)

Step-by-step explanation:

i got this on my quiz and i got it right! i  hoped this helped!!!

Answer:

$66 for 6 cars.

Step-by-step explanation:

This is a rather simple problem. To find the answer you must divide 44/4= 11. Now knowing that Chris earns $11 per car if you multiply 11x6= 66 you can find out Chris makes $66 for 6 cars.

Answer:

\(\textsf{Factored form}: \quad (a^2+4)(a-2)\)

\(\textsf{Standard form}: \quad a^3-2a^2+4a-8\)

Step-by-step explanation:

Given expression:

\(\dfrac{a^4-16}{a+2}\)

Rewrite the exponent 4 as 2·2 and 16 as 4²:

\(\implies \dfrac{a^{2 \cdot 2}-4^2}{a+2}\)

\(\textsf{Apply exponent rule} \quad a^{bc}=(a^b)^c\)

\(\implies \dfrac{\left(a^2\right)^2-4^2}{a+2}\)

\(\textsf{Apply the Difference of Two Squares Formula} \quad x^2-y^2=\left(x+y\right)\left(x-y\right):\)

\(\implies \dfrac{(a^2+4)(a^2-4)}{a+2}\)

Rewrite 4 in the second parentheses of the numerator as 2²:

\(\implies \dfrac{(a^2+4)(a^2-2^2)}{a+2}\)

Apply the Difference of Two Squares Formula to (a² - 2²):

\(\implies \dfrac{(a^2+4)(a+2)(a-2)}{a+2}\)

Cancel the common factor (a + 2):

\(\implies (a^2+4)(a-2)\)

Expand:

\(\implies a^2(a-2)+4(a-2)\)

\(\implies a^3-2a^2+4a-8\)

Answer:

y= mx+c

-4= -3/5(-5) + c

-4= -3/5 *-5+ c

-4=3+c

-4-3=c

-7=c

therefore the equation of the line is y=-3/5x-7

Step-by-step explanation:

the equation of a line is

y=mx +c

where y is the y coordinate

where m is the slope

where x is the x coordinate

where c is the y- intercept

Answer: A. Has a higher monthly bill but pays less out of pocket in the even of an accident.

Step-by-step explanation:

In auto insurance, a lower deductible means the customer has a higher monthly bill but pays less out of pocket in the event of an accident.

The protection against unforeseen financial losses you acquire when you purchase insurance. In the event that something bad occurs to you, the insurance company pays you or a person of your choosing. In the event of an accident, you can be liable for all expenses if you don't have insurance. Managing your risk is possible with insurance.

When you get sick, you have to pay less money upfront before your health insurance plan begins to pay with low-deductible plans. When you have low-deductible coverage, the trade-off is that your monthly premium will be higher.

In the case of vehicle insurance, a smaller deductible entails a higher monthly premium but fewer out-of-pocket costs for the consumer in the event of an accident.

Thus, in auto insurance, a lower deductible means the customer has a higher monthly bill but pays less out of pocket in the event of an accident.

Learn more about insurance here,

https://brainly.com/question/27822778

#SPJ6

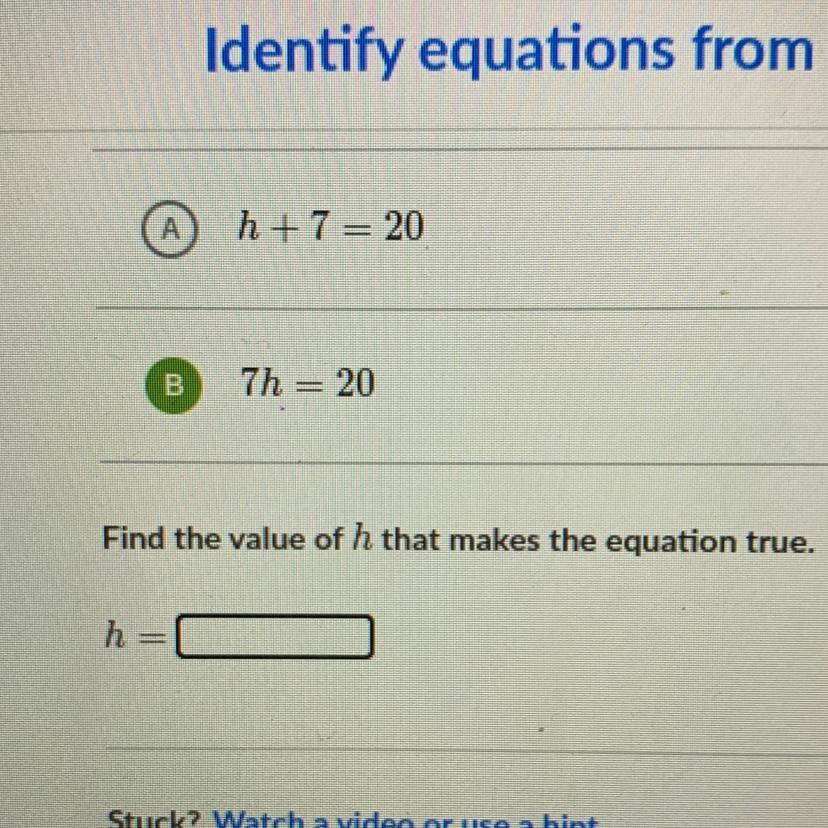
Answer:

Step-by-step explanation:

The meaning of the translation (x + 6, y + 10) is that all points in a coordinate plane are moved 6 units to the right and 10 units up.

In other words, for any point (x, y) in the original position, after the translation, the new coordinates would be (x + 6, y + 10). This means that the x-coordinate of each point is increased by 6 units, resulting in a shift to the right, and the y-coordinate is increased by 10 units, resulting in a shift upwards.

\(\\ \rm\Rrightarrow \dfrac{7513/100\times 5x^3}{3x^2}\)

\(\\ \rm\Rrightarrow \dfrac{75.13(5)x^3}{3x^2}\)

\(\\ \rm\Rrightarrow {125.22x}\)

Answer:

Step-by-step explanation:

y= x - 2

the graph would be parallel to y=x and every point would be shifted down 2 units

If you took any point on y = x and represented it as (x,y) then the new point would be (x,y - 2)

Answer:

\(\sqrt{16}\) is rational number

Step-by-step explanation:

Rational number is of the form p/q, where q ≠ 0. It may be a terminating number or non terminating repeating number.

√2 is irrational number as it is non terminating non repeating number

π is irrational number as it is non terminating non repeating number

√10 is irrational number as it is non terminating non repeating number.

\(\sqrt{16}=\sqrt{4*4}=4\)

\(\sqrt{16}\) is a rational number

Slope is change in y over the change in x.

Slope = (-7 - 2) / (-1 -2)

Slope = -9/-3

Slope = 3

The answer is \(-6x^2+2x+2\). To subtract \(7x^2-x-1\) from \(x^2+3x+3\), we need to first distribute the negative sign to each term in \(7x^2-x-1.\)

In algebra, an equation is a mathematical statement that asserts the equality between two expressions. It consists of two sides, often separated by an equal sign (=).

The expressions on each side of the equal sign may contain variables, constants, and mathematical operations.

Equations are used to represent relationships and solve problems involving unknowns or variables. The goal in solving an equation is to find the value(s) of the variable(s) that make the equation true.

This is achieved by performing various operations, such as addition, subtraction, multiplication, and division, on both sides of the equation while maintaining the equality.

Here, it gives us \(-7x^2+x+1\). Now we can line up the like terms and subtract them.
\(x^2 - 7x^2 = -6x^2\)
3x - x = 2x
3 - 1 = 2

Putting these results together, we get:
\(x^2+3x+3x^2 - (7x^2-x-1) = -6x^2+2x+2\)

Therefore, the answer is \(-6x^2+2x+2.\)

For more question on subtract

https://brainly.com/question/28467694

#SPJ8

Answer:

-3<x<5

Step-by-step explanation:

Given the inequality 2x-3<7 and 5-x<8

Solve 2x-3<7

Add 3 to both sides

2x-3+3 < 7+3

2x < 10

2x/2 < 10/2

x < 5

Solve 5-x<8

subtract 5 from both sides:

5-x-5<8-5

-x < 3

multiply both sides  by -1

-(-x) > -3

x > -3

-3<x

Combine both solutions x < 5 and -3<x

-3<x<5

The solution to the compound inequality is -3<x<5

Answer:

h= the number 7 duh-

Step-by-step explanation:

Answer:

Step-by-step explanation:

In the given triangle AED, segments GB and FC are parallel to base ED. Points G and F are on segment AE in that order. Lengths AG=2, GF=5, FE=3, GB=6, and CD=7 are given. You want the lengths of AB, BC, FC, and ED.

Segments of transversals crossed by parallel lines are proportional:

  AG : GF : FE = AB : BC : CD

  2 : 5 : 3 = AB : BC : 7

Multiplying the first ratios by 2 1/3 will give the second ratios:

  2 : 5 : 3 = 4 2/3 : 11 2/3 : 7

This lets us conclude ...

  AB = 4 2/3

  BC = 11 2/3

Corresponding segments of similar triangles are proportional:

  AG : GB = FA : FC = AE : ED

  2 : 6 = (5+2) : FC = (5+2+3) : ED

We notice the second number in the first ratio is 3 times the first number. That means these ratios are ...

  2 : 6 = 7 : 21 = 10 : 30

This lets us conclude ...

  FC = 21

  ED = 30

The lengths of the missing sides are calculated to be

The parallel lines in the figure created similarity between the dimensions, this makes the ratio of the dimensions equal

The given dimensions that is used to find the missing sides

Solving for AB

AB / CD = AG / FE

AB / 7 = 2 / 3

cross multiplying

3 * AB = 7 * 2

AB = 14/3 = 4.667

Using AB, GF is calculated

AB / BC = AG / GF

14/3 / BC = 2 / 5

cross multiplying

BC = (5 * 14/3) / 2

BC = 35/3 = 11.667

Solving for FC

GB / FC = AG / A'F

6 / FC = 2 / (2 + 5)

cross multiplying

2 * FC = 6 * 7

FC = 42/2 = 21

Solving for ED

GB / ED = AG / AE

6 / ED = 2 / (2 + 5 + 3)

cross multiplying

2 * ED = 6 * 10

ED = 60/2 = 30

Learn more about similar polygons at:

https://brainly.com/question/1493409

#SPJ1

To determine whether a vector is in the orthogonal complement of W (denoted as W⊥), we need to check if the vector is orthogonal (perpendicular) to all vectors in W.

The set W consists of all vectors of the form (x, y, x + y) where x and y are real numbers.

Let's analyze each vector:

v = (-1, -1, 1):

To check if v is in W⊥, we need to verify if v is orthogonal to all vectors in W.

Consider an arbitrary vector w = (x, y, x + y) in W. The dot product of v and w is given by:

v · w = (-1)(x) + (-1)(y) + (1)(x + y) = -x - y + x + y = 0

Since the dot product is zero for any vector w in W, we can conclude that v is orthogonal to all vectors in W. Therefore, v is in W⊥.

v = (-2, -7, 11):

Similarly, we need to check if v is orthogonal to all vectors in W.

Consider an arbitrary vector w = (x, y, x + y) in W. The dot product of v and w is given by:

v · w = (-2)(x) + (-7)(y) + (11)(x + y) = -2x - 7y + 11x + 11y = 9x + 4y

For v to be orthogonal to all vectors in W, the dot product v · w should be zero for any vector w in W. However, 9x + 4y is not always zero for all x and y, so v is not orthogonal to all vectors in W. Therefore, v is not in W⊥.

v = (-2, -2, 2):

As before, we need to check if v is orthogonal to all vectors in W.

Consider an arbitrary vector w = (x, y, x + y) in W. The dot product of v and w is given by:

v · w = (-2)(x) + (-2)(y) + (2)(x + y) = -2x - 2y + 2x + 2y = 0

Since the dot product is zero for any vector w in W, we can conclude that v is orthogonal to all vectors in W. Therefore, v is in W⊥.

In summary:

v = (-1, -1, 1) is in W⊥.

v = (-2, -7, 11) is not in W⊥.

v = (-2, -2, 2) is in W⊥.

Learn more about vector at https://brainly.com/question/29368578

#SPJ11

Answer:

see explanation

Step-by-step explanation:

Both sequences have a common difference between consecutive terms, that is

2 - 1 = 3 - 2 = 4 - 3 = 1

This indicates the sequence is arithmetic with n th term

\(a_{n}\) = a₁ + (n - 1)d

where a₁ is the first term and d the common difference

Here a₁ = 1 and d = 1 , thus

\(a_{n}\) = 1 + n - 1 = n

--------------------------------------------------------------------

Similarly

d = 9 - 5 = 13 - 9 = 17 - 13 = 4 and a₁ = 5 , then

\(a_{n}\) = 5 + 4(n - 1) = 5 + 4n - 4 = 4n + 1

Answer:

(d/2)^2 pi

Step-by-step explanation:

To find the area of a circle the formula is A=pi times radius sqaured. Since we do not have the radius we need to find it. The radius will always be half the diameter hence the (d/2). This will give us the radius, next is just to complete the area formula by squaring the radius and multiplying it by pi.  i hope this helps :)

The circle's area, in function of it's diameter, is given by:

\(A = \frac{\pi d^2}{4}\)

----------------------

\(A = \pi r^2\)

\(A = \pi r^2\)

\(A = \pi (\frac{d}{2})^2\)

\(A = \pi \frac{d^2}{4}\)

\(A = \frac{\pi d^2}{4}\)

Which is the area of a circle of diameter d.

A similar problem is given at https://brainly.com/question/16891462

The given statement to this question is true

What is an optimal solution?

An acceptable solution where the objective function reaches its highest (or minimum) value, such as the most profit or the lowest cost, is referred to as an optimal solution. When there are no other practical solutions with superior objective function values, the solution is said to be globally optimal.

Here, we have

The global optimum point may be superior to nearby points, but the local optimum point is the true optimal solution to a nonlinear programming problem.

Because when own linear model is solved this solution is merely local optimum.

The solver should consider that other local optimum Amy does not exist with better object values. The globally optimal solution is one where there are no feasible solutions with a better objective function.

However many nonlinear problems are non-convex and are likely to have multiple locally optimal solutions. The local optimum point is the true optimal solution for the nonlinear programming model.

Hence, the given statement to this question is true.

To learn more about the optimal solution from the given link

https://brainly.com/question/15356519

#SPJ4

The removable discontinuity of the function is x-2/(x-2)(x+4).

Given, we have the following functions:

a. x-2/(x-2)(x+4)

separate the terms:

= x-2/x-2 × 1/x+4

cancel the like terms:

= 1 × 1/x+4

hence x-2/(x-2)(x+4) has a removable discontinuity.

A point on the graph that is undefinable or does not fit the remainder of the graph is referred to as a removable discontinuity. A detachable discontinuity can be generated in one of two ways. The function can be defined to have a blip, or it can have a common factor in both the numerator and the denominator.

When the two-sided limit at c exists but isn't equal to f(c), the discontinuity at c is referred to as detachable.

Hence the from the given functions the function which have a removable discontinuity is x-2/(x-2)(x+4)

Learn more about Removable continuity here:

brainly.com/question/24637240

#SPJ1

Answer:

23 females are right handed and 9 are left handed

Step-by-step explanation:

So to get this answer :

18 OF THE 41 RIGHT HANDED EMPLOYEES ARE MALE.

The statement means that there are 41 right handed employees and 18 of those are male thus the remaining are FEMALE.

To find the number of right handed employees who are female just subtracted 18 from 41 ( becaus etotal number of right handed males is 18 and the total number of right handed employees is 41.)

SO 23 FEMALES IN THE COMPANY ARE RIGHT HANDED.

Because 23 females are right handed that means to get the number of left handed females you subtract the total number of right handed females from the total number of females in the company THUS:

32 - 23 = 9 LEFT HANDED FEMALES

HOPE IT HELPED

Answer:

after simplifying, we get,

23/6

Step-by-step explanation:

(2/3+5/2-7/3)+(3/2+7/3-5/6)

We simplify,

\((2/3+5/2-7/3)+(3/2+7/3-5/6)\\(2/3-7/3+5/2)+(3/2+7/3-5/6)\\(5/2-5/3)+(9/6+14/6-5/6)\\(15/6-10/6)+((9+14-5)/6)\\(15-10)/6+(23-5)/6\\5/6+18/6\\(5+18)/6\\23/6\)

Answer:

Please find attached the required inverse of a function chart

Step-by-step explanation:

The inverse of a function is found by reversing the operations of the  function

The inverse of the function f(x) = 2·x - 4 is found as follows;

x = 2·x - 4

x + 4 = 2·x

x = (x + 4)/2 = x/2 + 2

Therefore, the inverse of the function f(x) = 2·x - 4 is f(x) = x/2 + 2

The inverse function is plotted by generating data points as follows;

\({}\)x         \({}\)          f(x)

0                2

1                  2.5

2                 3

3                  3.5

4                   4

5                   4.5

6                   5

7                   5.5

8                   6

9                   6.5

10                  7

11 \({}\)                   7.5

12\({}\)                    8

13                 8.5

14                  9

15                  9.5

16               10

Answer:

28

Step-by-step explanation:

V = 4 * 1 * b = 8

b = 2

SA = 2(4 + 1) * 2 + 2(4)1)

SA = 28

Answer: 28 ft²

Answer:

28 = surface area

Step-by-step explanation:

b is 2

have a great day!

Answer:

The answer is x=12

Step-by-step explanation:

2*12= 24-4 = 20/5=4

the answer is x=12

Answer:

Here,

A=-7

B=12

Length of AB=?

Now, We know that,

Length of AB=-7-12

=-19

Thus, the length of AB is -19

If in circle A, diameter EC is perpendicular to chord BD, and arc EB measures 62 degrees, the measure of arc ED is 208 degrees.

To solve the problem, we need to use the relationship between arcs, angles, and chords in a circle.

Since diameter EC is perpendicular to chord BD, we know that angle EBD is a right angle.

Arc EB measures 62 degrees, and we know that angle EBD is 90 degrees. Therefore, arc ED must measure:

360 degrees - arc EB - angle EBD

= 360 degrees - 62 degrees - 90 degrees

= 208 degrees

So, the measure of arc ED is 208 degrees.

To learn more about angle click on,

https://brainly.com/question/22908715

#SPJ1

The height of the 10th bounce of the ball will be 0.6 feet.

A geometric sequence is a sequence in which each term is found by multiplying the preceding term by the same value.

The nth term of the geometric sequence is given by

\(\sf T_n=ar^{n-1}\)

Where,

According to the given question.

During the first bounce, height of the ball from the ground, a = 4.5 feet

And, the each successive bounce is 73% of the previous bounce's height.

So,

During the second bounce, the height of ball from the ground

\(\sf = 73\% \ of \ 10\)

\(=\dfrac{73}{100}(10)\)

\(\sf = 0.73 \times 10\)

\(\sf = 7.3 \ feet\)

During the third bounce, the height of ball from the ground

\(\sf = 73\% \ of \ 7.3\)

\(=\dfrac{73}{100}(7.3)\)

\(\sf = 5.33 \ feet\)

Like this we will obtain a geometric sequence 7.3, 5.33, 3.11, 2.23,...

And the common ratio of the geometric sequence is 0.73

Therefore,

The sixth term of the geometric sequence is given by

\(\sf T_{10}=10(0.73)^{10-1\)

\(\sf T_{10}=10(0.73)^{9\)

\(\sf T_{10}=10(0.059)\)

\(\sf T_{10}=0.59\thickapprox0.6 \ feet\)

Hence, the height of the 10th bounce of the ball will be 0.6 feet.

Find out more information about geometric sequence here:

brainly.com/question/11266123

The density of metal is 7022.2 kg/m^3 and the metal is not gold. We were cheated.

In the given question, we purchase a rectangular piece of metal that has dimensions 5.0 x 15.0 x 30.0 mm and mass 0.0158 kg.

The seller tells you that the metal is gold.

We have to find the density of piece.

Then Given ,

Mass = 0.0158 kg

Volume = 5.0 mm * 15.0 mm * 30.0 mm

Density = mass / volume

Putting the values

Density = 1.58 * 10^(-2) kg/(5.0*10^{-3}*15.0*10^{-3}*30.0*10^{-3}) m^3

Density = 7022.2 kg/m^3

The density of metal is 7022.2 kg/m^3 and the metal is not gold. We were cheated.

To learn more about density of metal link is here

brainly.com/question/29009519

#SPJ4