The circle below has center 0, and its radius is 4 mm. Given that m ZAOB = 50°, find the length of the major arc ACB.
Give an exact answer in terms of it, and be sure to include the correct unit in your answer.
Help me pls

Answers
\(\textit{arc's length}\\\\ s=\cfrac{r\theta \pi }{180}~~ \begin{cases} r=radius\\ \theta =\stackrel{in~degrees}{angle}\\[-0.5em] \hrulefill\\ r=4\\ \theta =50 \end{cases}\implies s=\cfrac{(4)(50)\pi }{180}\implies s=\cfrac{10\pi }{9}~mm\)
Related Questions
For the function -3x^2+12
find the interval over which the function is increasing.
Answers
Answer:
The given function is:
f(x) = -3x^2 + 12
To find the interval over which the function is increasing, we need to find the critical points of the function.
f'(x) = -6x
The critical point is where f'(x) = 0
-6x = 0
x = 0
Now, we need to check the sign of f'(x) on either side of the critical point to determine whether the function is increasing or decreasing.
If x < 0, then f'(x) < 0, so the function is decreasing.
If x > 0, then f'(x) > 0, so the function is increasing.
Therefore, the interval over which the function is increasing is:
(0, infinity)
Step-by-step explanation:
gg
HELP ME!! LOOK AT PICTURE. 100 POINTS

Answers
Answer:
Step-by-step explanation:
Domain is the input, what's the input when they can have a max of 110 people?
0 to 110 , right?
Please help me will give points

Answers
Answer:
\(6 + 6 < > 7\)
yk maths pooo
A group of 6 students was asked, "How many hours did you watch television last week?" Here are their responses.11, 11, 4, 9, 10, 17Find the mean number of hours for these students.If necessary, round your answer to the nearest tenth.hours
Answers
The mean number of hours for these students 10.3
Explanation:Given the following data:
11, 11, 4, 9, 10, 17
The mean is the sum of the data divided by the number of elements in the data.
Sum of data is:
11 + 11 + 4 + 9 + 10 + 17 = 62
Number of elements in the data is:
6
The mean is now:
62/6 = 10.3
Ol
© The ratio of boys to girls in a class is 5:4. There are 36 students in the class. How many
students are girls?
Answers
Answer:
16
Step-by-step explanation:
\(no \: of \: girls = \frac{4}{5 + 4} \times 36 \\ \\ = \frac{4}{9} \times 36 \\ \\ = 4 \times 4 \\ \\ = 16\)
Answer:
Step-by-step explanation:
let the ratio of boys and girls be 5x and 4x
According to question,
5x+4x = 36
or, 9x= 36
x=4
number of boys = 5x
= 5·4= 20
number of girls = 4x
= 4.4=16
therefore the total no of boys is 20 ans girls is 16
A prism with a volume of 3125 ft³ is scaled down to a volume of 200 ft³. What is the scale factor? Enter your answer, as a decimal or a fraction in simplest form, in the box.
Answers
Answer:
2/5 or .4
Step-by-step explanation:
the first answer is correct. This is just in case they ask for the answer as a fraction. :)
HELP ME PLEASE!
Delbert needs to mix a 20% acid solution with a 50% acid solution to create
100 milliliters of a 26 % solution. How many millileters of each solution must Delbert use?
Answer: Delbert must mix
_____ milliliters of the
20% solution and
_____ milliliters of the 50% solution.
Answers
Answer:
Step-by-step explanation:
26% is (26-20)/(50-20) = 6/30 = 1/5 of the way between 20% and 50%. That means 1/5 of the solution is 50% acid.
50% acid: 1/5 · 100 mL = 20 mL
20% acid: 100 mL -20 mL = 80 mL
Delbert must mix 80 mL of 20% acid and 20 mL of 50% acid.
_____
Maybe you'd like to see an equation. Let x represent the amount of 50% acid required. Then 100-x is the amount of 20% acid needed. The amount of acid in the mix is ...
0.50(x) +0.20(100 -x) = 0.26(100)
(0.50 -0.20)x = (0.26 -0.20)100 . . . . subtract 0.20(100)
x = (0.26 -0.20)/(0.50 -0.20)×100 = 20
This last expression should look a lot like the one we started with in this answer. It shows you how you can almost write down the answer to mixture problems without a lot of work.
3. How is the circumference of a circle related to the length of its diameter?
Answers
Step-by-step explanation:
.The circumference is the distance around the circle. The circumference is equal to two times pi times the radius (C = 2*pi*r). Because the diameter is equal to two times the radius, the circumference is equal to the diameter times pi (C = D*pi), where pi is about 3.14… The diameter of a circle is 2 units.
please help like waaa everywhere it comes up that its impossible

Answers
Answer:
Step-by-step explanation:
If we subtract 7 from both sides, we get -2 on the right. This is not possible, since absolute values are always 0 or greater.
Which expression can be simplified as StartFraction 1 Over n Superscript 18 Baseline EndFraction? (n squared) Superscript 9 (n Superscript negative 9 Baseline) Superscript negative 2 (n Superscript negative 6 Baseline) Superscript negative 3 (n Superscript negative 3) Superscript 6
Answers
The expression (n²)⁹ (n⁻⁹)⁻² (n⁻⁶)⁻³ (n⁻³)⁶ can be simplified as 1/n¹⁸.
To simplify the given expression, let's work on each factor separately:
\((n^2)^9:\) When we raise a power to another power, we multiply the exponents.
Therefore,\((n^2)^9\) simplifies to \(n^{(2 \times 9)} = n^{18\)
\((n^{(-9)})^{-2}:\) When we raise a negative exponent to another power, it becomes positive.
Therefore,\((n^{(-9)})^{-2}\) simplifies to \(n^{(9 \times {-2})} = n^{(-18)}.\)
\((n^{(-6)})^{-3}:\) Similar to the previous step, when we raise a negative exponent to another power, it becomes positive.
Thus, \((n^{(-6)})^{-3}\) simplifies to \(n^{(6 \times -3) }= n^{(-18)}.\)
\((n^{(-3)})^6:\) Once again, we raise a negative exponent to another power, making it positive.
Therefore,\((n^{(-3)})^6\) simplifies to \(n^{(3 \times 6)}= n^{18}.\)
Now, let's combine all the simplified factors:
\((n^2)^9 \times (n^{(-9)})^-2 \times (n^{(-6)})^-3 \times (n^{(-3)})^6\)
\(= n^{18} \times n^{18} \times n^{18}\times n^{18}\)
When we multiply variables with the same base, we add the exponents. Therefore, the expression simplifies to:
\(n^{(18 + 18 + 18 + 18) }= n^{72\)
So, the given expression simplifies to \(n^{72}.\)
For similar question on expression.
https://brainly.com/question/112703
#SPJ8
What subset, a, of the sample space represents the complement of the event in which camille is the final swimmer? a = {cba, cab, bca, acb} a = {abc, bac} a = {cba, cab, bac, bca, acb, abc} a = {ab, ba}
Answers
Answer:
the first choice :)
Step-by-step explanation:
Answer:
Option A: A = {CBA, CAB, BCA, ACB}
Suppose that your company has just developed a new screening test for a disease and you are in charge of testing its validity and feasibility. You decide to evaluate the test on 1000 individuals and compare the results of the new test to the gold standard. You know the prevalence of disease in your population is 30%. The screening test gave a positive result for 310 individuals. 290 of these individuals actually had the disease on the basis of the gold standard determination.
Answers
The true positive rate, also known as sensitivity, is 96.7%.
The following is the calculation of the test validity:
True positive rate: True positive rate (sensitivity) = (Number of true positive results) ÷ (Number of people with the disease in the study population)100% = (290) ÷ (300)100% = 96.7%
False positive rate: False positive rate = (Number of false positive results) ÷ (Number of people without the disease in the study population)100% = (20) ÷ (700)100% = 2.9%
True negative rate: True negative rate (specificity) = (Number of true negative results) ÷ (Number of people without the disease in the study population)100% = (680) ÷ (700)100% = 97.1%
False negative rate: False negative rate = (Number of false negative results) ÷ (Number of people with the disease in the study population)100% = (10) ÷ (300)100% = 3.3%
Accuracy:
Accuracy = (Number of true results) ÷ (Total number of people in the study population)100% = (970) ÷ (1000)100% = 97%
Positive predictive value: Positive predictive value = (Number of true positive results) ÷ (Number of people with positive results)100% = (290) ÷ (310)100% = 93.5%
Negative predictive value:Negative predictive value = (Number of true negative results) ÷ (Number of people with negative results)100% = (680) ÷ (690)100% = 98.6%
False omission rate:False omission rate = (Number of false negative results) ÷ (Number of people with negative results)100% = (10) ÷ (690)100% = 1.4%
Thus, The true positive rate, also known as sensitivity, is 96.7%.
Know more about sensitivity here:
https://brainly.com/question/14472410
#SPJ11
Two trucks leave a factory at the same time. One travels east at 60 miles per hour, and the other travels west at 30 miles per hour. In how many hours will they be 150 miles apart? A 1-2/3 hours B 2 hours C 2-1/2 hours D 5 hours
Answers
If a+b+c=0 , a=6, b=7 and c =√127, find the angle between a and b
Answers
The angle between vector a and vector b is θ = 60° .
In the question ,
it is given that ,
a+b+c=0 , and the modulus values of the vectors a , b and c are given as |a| = 6 , |b| = 7 and |c| = √127 ,
we have to find the angle between the vectors a and b
So , a + b = -c
|a + b| = |-c|
on squaring , we get
|a + |b|² = |-c|²
|a|² + |b|² + 2abCosθ = |c|²
36 + 49 + 2*6*7*Cosθ = 127
85 + 84Cosθ = 127
84Cosθ = 127 - 85
84Cosθ = 42
Cosθ = 42/84
Cosθ = 1/2
So , θ = 60° .
Therefore , The angle between vector a and vector b is θ = 60° .
The given question is incomplete , the complete question is
If a+b+c=0 , |a| = 6 , |b| = 7 and |c| = √127, find the angle between vector a and vector b .
Learn more about Vectors here
https://brainly.com/question/28529274
#SPJ1
what is x and y? i am having trouble finding what x and y are
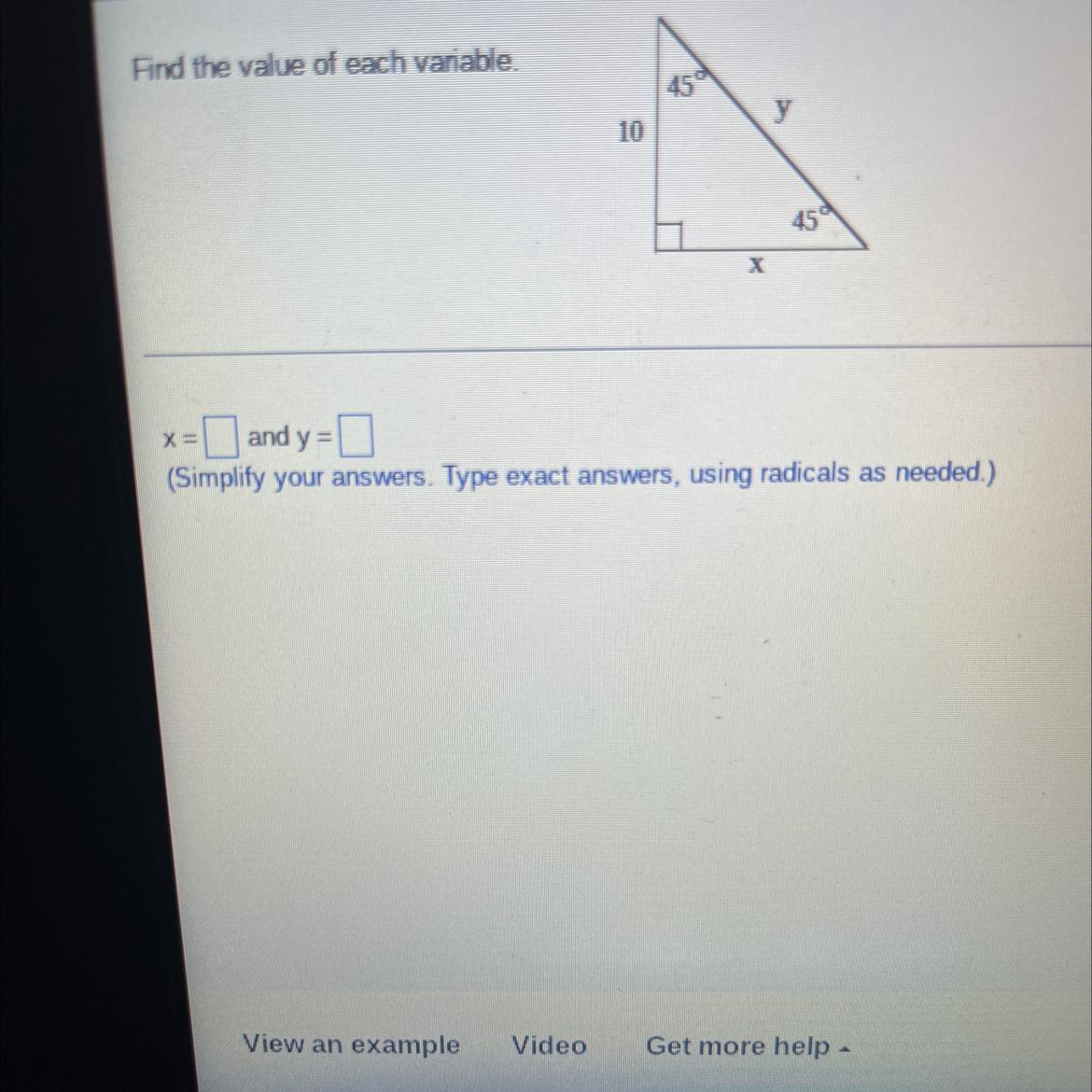
Answers
Answer:
x = 10
y =10√2
Step-by-step explanation:
45° - 45° - 90° triangle:The ratio of the sides of 45°- 45° - 90° triangle is a : a : a√2
The side opposite to angle 45° is a
a = 10
⇒ x = a
\(\sf \boxed{\bf x = 10}\)
The side opposite to 90° is a√2
y = a√2
= 10√2
\(\sf \boxed{\bf y= 10\sqrt{2}}\)
Answer:
y = 14.1 or 10√2Step-by-step explanation:
is an isosceles right triangle, so x = 10
to find y we use pythagoras
y = √(10²+10²)
y = √200
y = 14.1 or 10√2

Solve by combining:
-x-y=6
5x-7y=66
Answers
Answer:
x = 2
y = 8
Step-by-step explanation:
-x - y = 6
5x - 7y = 66
-x - y = 6
x = -y - 6
5x - 7y = 66
5 ( -y - 6 ) - 7y = 66
-12y - 30 = 66
-12y = 96
y = -8
x = -y - 6
x = 8 - 6
x = 2
Use the slope formula to identify the slope between two given ordered pairs,
1. (-6,4) and (-6,5)
2. (8,-4) and (-2,7)
Answers
1. (5-4)/(-6-(-6)) = 1/0 = undefined
2. (7-(-4)/(-2-8) = 11/-10 = -11/10
Solution: 1. Undefined, 2. -11/10
if p = 2^k + 1 is prime, show that every quadratic nonresidue of p is a primitive root of p.
Answers
Every quadratic nonresidue of p is a primitive root of p, when p = 2^k + 1 is primeIf p = 2^k + 1 is a prime number, we want to show that every quadratic nonresidue of p is a primitive root of p.
In other words, we aim to prove that if an element x is a quadratic nonresidue modulo p, then it is also a primitive root of p.
Let's assume p = 2^k + 1 is a prime number. To prove that every quadratic nonresidue of p is a primitive root of p, we can use the properties of quadratic residues and quadratic nonresidues.
A quadratic residue modulo p is an element y such that y^((p-1)/2) ≡ 1 (mod p), while a quadratic nonresidue is an element x such that x^((p-1)/2) ≡ -1 (mod p).
Now, let's consider an element x that is a quadratic nonresidue modulo p. We want to show that x is a primitive root of p.
Since x is a quadratic nonresidue, we know that x^((p-1)/2) ≡ -1 (mod p). By Euler's criterion, this implies that x^((p-1)/2) ≡ -1^((p-1)/2) ≡ -1^2 ≡ 1 (mod p).
Since x^((p-1)/2) ≡ 1 (mod p), we can conclude that the order of x modulo p is at least (p-1)/2. However, since p = 2^k + 1 is a prime, the order of x modulo p must be equal to (p-1)/2.
By definition, a primitive root of p has an order of (p-1). Since the order of x modulo p is (p-1)/2, it follows that x is a primitive root of p.
Learn more about Euler's criterion here:
brainly.com/question/12977984
#SPJ11
Jessica’s car depreciates in value by 11% per year. Jessica bought her car for £21000. Work out how much her car will be worth after 7 years, giving your answer to the nearest penny.
Answers
Answer:
Brainliest
Step-by-step explanation:
21,000 x 0.89^7 =
9,288.58032806109 = 9288.58
Answer:
£9288.58
Step-by-step explanation:
Initial price= 21000
Price drop rate= 11%
Time= 7 years
Price at the end of 7 years: £21000*((100-11)/100)^7= £9288.58
If the distance covered by an object in time t is given by s(t)=t²+5t
, where s(t) is in meters and t is in seconds, what is the distance covered in the interval between 1 second and 5 seconds?
Answers
s(1) = 1^2 + 5(1) = 1 + 5 = 6 (m/s)
s(5) = 5^2 + 5(5) = 25 + 25 = 50 (m/s)
Therefore the distance covered would be:
50 - 6 = 44m/s
The distance in the interval between 1 second and 5 seconds where the distance covered by an object is s(t) = t^2 + 5t is 44m/s
Approximately how many people cross Shibuya Crossing each minute?
Choose 1 answer:
Answers
When I searched it up on the internet, the result was:
"During its busiest times, an estimated 1,000 to 2,500 people forge their way across this intersection every two minutes, enough to quickly fill up a football stadium."
Percentage change
….

Answers
Answer:
80%
Step-by-step explanation:
Change is (45-25)/25*100=(20/25)*100=80%
What does a residual value of 1. 3 mean when referring to the line of best fit of a data set? A data point is 1. 3 units above the line of best fit. A data point is 1. 3 units below the line of best fit. The line of best fit has a slope of –1. 3 The line of best fit has a slope of 1. 3.
Answers
You can use the fact that a residual value is obtained by subtracting the prediction by the line of best fit from the actual data value we have.
The residual value 1.3 when referring to the line of best fit of a data set means:
Option B: A data point is 1.3 units below the line of best fit
What is a residual value and how is it calculated?
First of all, this whole story starts with data. We get data and we try to fit a line which can best imitate the way data is lying on the coordinate plane.
Remember that on a 2d coordinate cartesian plane, we have (x,y) called as point on plane and x is abscissa and y is called ordinate.
Let the best fit line be denoted by y = mx + c (assuming we're working with 2d data) with slope m and y-intercept c.
Now, this line is used to predict where can the next data point may lie.
When this best fit line is used to predict already present data point, we get the error that best fit line made when predicting the real data.
This is measured by "residual value"
For data point with ordinate b, we suppose get prediction as y
Then we have the residual value as y - b.
Remember, the prediction is before the real data point's ordinate.
How to know what does 1.3 residual value mean?Let the real value be b and the predicted value be y from which this residual was calculated.
Then we have:
y - b = 1.3
y = 1.3 + b
Thus, we see that prediction is bigger than the real data point's y-ordinate. Since y axis has increasing value as we go higher and higher vertically, thus this prediction value's ordinate is higher than that of real value's ordinate.
The prediction, since shows the height of best fit line on that input point, thus we have:
Option B: A data point is 1.3 units below the line of best fit.
Learn more about line of best fit here:
https://brainly.com/question/2396661
Answer:
Answer B
Step-by-step explanation:
I'm smart please ad brainliest! :P
4 questions! Write an equation in slope-intercept form for each of the following:
1) Slope -4 ; y-intercept 6
2) Slope 3 ; passes through (2,5)
3) (1,-1) , (-2,0)
4) (0,0) (4 - 3 1/2)
These are practice questions! ASAP!
Answers
The equation of line slope intercept form:
1. y = -4x+6.
2. y = 3x -1
3. y = (-x-2)/3
4. Inappropriate coordinates.
What is Straight Line?A straight line is an infinite length line that does not have any curves on it. A straight line can be formed between two points also but both the ends extend to infinity.
1. Given; Slope (m) = -4 ; y-intercept (c) = 6
Slope intercept form of straight line:
y = mx + c
y = -4x + 6
2. Slope 3 ; passes through (2,5)
Equation of line;
(y - y₁) = m(x - x₁)
y - 5 = 3(x - 2)
y -5 = 3x - 6
y = 3x - 6 + 5
y = 3x -1
3. passing point (1,-1) , (-2,0)
(y - y₁) = (y₂-y₁)/(x₂-x₁) (x - x₁)
(y - (-1)) = (0-(-1))/(-2-1) (x - 1)
y + 1 = 1/(-3) (x-1)
-3(y+1) = x -1
-3y - 3 = x - 1
-3y = x - 1 + 3
-3y = x + 2
y = (-x-2)/3
4. Coordinates are inappropriate.
Learn more about Straight line from:
https://brainly.com/question/27560536
#SPJ1
4. Calculate the values for the ASN curves for the single sampling plan \( n=80, c=3 \) and the equally effective double sampling plan \( n_{1}=50, c_{1}=1, r_{1}=4, n_{2}=50, c_{2}=4 \), and \( r_{2}
Answers
Single Sampling Plan: AQL = 0, LTPD = 3.41, AOQ = 1.79 Double Sampling Plan: AQL = 0, LTPD = 2.72, AOQ = 1.48
The values for the ASN (Average Sample Number) curves for the given single sampling plan and double sampling plan are:
Single Sampling Plan (n=80, c=3):
ASN curve values: AQL = 0, LTPD = 3.41, AOQ = 1.79
Double Sampling Plan (n1=50, c1=1, r1=4, n2=50, c2=4, r2):
ASN curve values: AQL = 0, LTPD = 2.72, AOQ = 1.48
The ASN curves provide information about the performance of a sampling plan by plotting the average sample number (ASN) against various acceptance quality levels (AQL). The AQL represents the maximum acceptable defect rate, while the LTPD (Lot Tolerance Percent Defective) represents the maximum defect rate that the consumer is willing to tolerate.
For the single sampling plan, the values n=80 (sample size) and c=3 (acceptance number) are used to calculate the ASN curve. The AQL is 0, meaning no defects are allowed, while the LTPD is 3.41. The Average Outgoing Quality (AOQ) is 1.79, representing the average quality level of outgoing lots.
For the equally effective double sampling plan, the values n1=50, c1=1, r1=4, n2=50, c2=4, and r2 are used. The AQL and LTPD values are the same as in the single sampling plan. The AOQ is 1.48, indicating the average quality level of outgoing lots in this double sampling plan.
These ASN curve values provide insights into the expected performance of the sampling plans in terms of lot acceptance and outgoing quality.
To learn more about average click here
brainly.com/question/30873037
#SPJ11
if i had 33 watermelons in one hand and 21 apples in another
what do i have?
Answers
Answer:
Your hands full
Step-by-step explanation:
Answer:
wut?..
If you really mean it then you will have 54 fruits
when a number is divided by 37, the quotient is 57, and the remainder is 29. what is the number
Answers
Answer:
Step-by-step explanation:
Hello, it means that the number is
57 * 37 + 29 = 2138
Thank you
Solve the following quadratic equation for all values of xx in simplest form.(Solving Quadratics with Square Roots (Level 1)
(x+10)^2-8=8
Answers
Then u have x^2+100-8=8
Then u have to bring 8 over the equality sign and minus it with the other -8 to get -16
It becomes x^2+100-16
Then u find the factors of 16 which add up to 100 but since that’s not possible with the formula I normally use u have to do
X=-b+&-rootb^2-4ac/2ac then simplify your answer and substitute in equation twice with plus and minus to get your answer
(I might be wrong tho)
NEED HELP ASAP Find the value of x. Round to the nearest tenths place.

Answers
Answer:
7.1
Step-by-step explanation:
Tan(55)×5= 7.14= 7.1
Answer: 7.14
Step-by-step explanation:
(x/5) = tan55
x = 5 tan55
x = 7.14
Exercise 8-3 Algo A simple random sample of 35 observations is derived from a normally distributed population with a known standard deviation of 6.3. [You may find it useful to reference the z table.]
a. Is the condition that X− is normally distributed satisfied? Yes No
b. Compute the margin of error with 95% confidence. (Round intermediate calculations to at least 4 decimal places. Round "z" value to 3 decimal places and final answer to 2 decimal places.)
c. Compute the margin of error with 90% confidence. (Round intermediate calculations to at least 4 decimal places. Round "z" value to 3 decimal places and final answer to 2 decimal places.)
d. Which of the two margins of error will lead to a wider interval? The margin of error with 90% confidence. The margin of error with 95% confidence.
Answers
a. Yes, the condition that X- is normally distributed is satisfied.
b. The margin of error with 95% confidence is 2.68.
c. The margin of error with 90% confidence is 2.16.
d. The margin of error with 95% confidence will lead to a wider interval than the margin of error with 90% confidence.
a. Yes, the condition that X- is normally distributed is satisfied because the sample size n = 35 is sufficiently large, and the population is normally distributed.
b. For a 95% confidence level, the z-value is 1.96 (from the z-table). The margin of error (ME) can be calculated as
ME = z-value * (standard deviation / √(n))
ME = 1.96 * (6.3 / √(35))
ME ≈ 2.68
Therefore, the margin of error with 95% confidence is 2.68.
c. For a 90% confidence level, the z-value is 1.645 (from the z-table). The margin of error (ME) can be calculated as
ME = z-value * (standard deviation / √(n))
ME = 1.645 * (6.3 / √(35))
ME ≈ 2.16
Therefore, the margin of error with 90% confidence is 2.16.
d. The margin of error with 95% confidence (2.68) will lead to a wider interval than the margin of error with 90% confidence (2.16). This is because a higher confidence level requires a larger margin of error to ensure that the interval contains the true population parameter with a higher probability.
Learn more about margin of error here
brainly.com/question/29101642
#SPJ4