The bearing of a ship from Hartland Point is 070°. Its bearing from Appledore is 320º. where would the ship be

Answers
Answer:
See attached
Step-by-step explanation:
Approximate angle drawings......

Related Questions
3/14
turned into a decimal
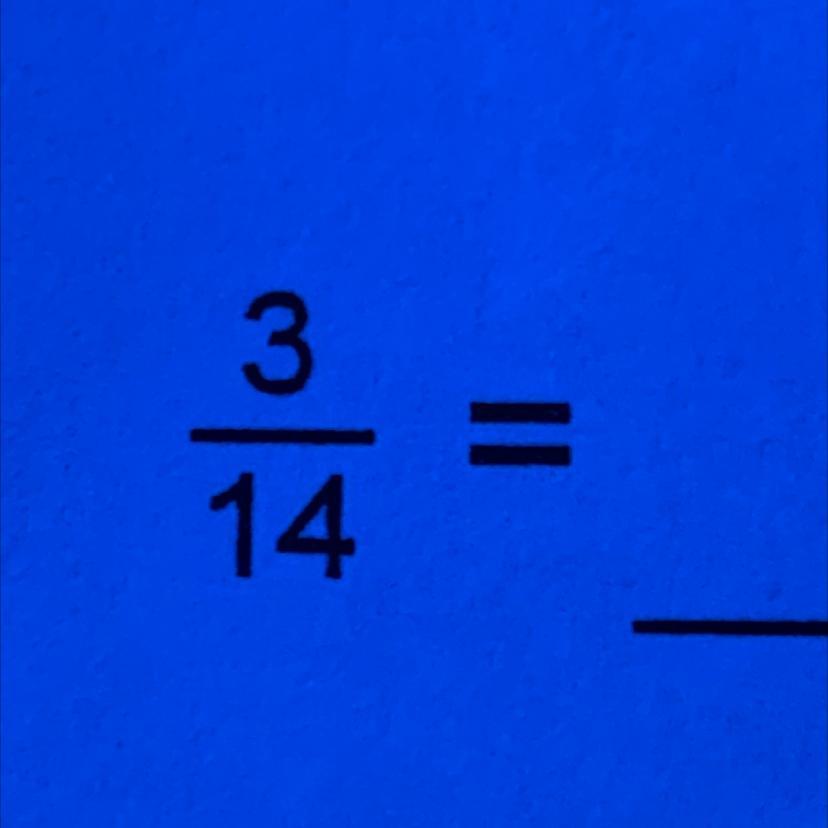
Answers
Answer:
i believe it is 0.2143
Step-by-step explanation:
Answer:
0.21428571428
Step-by-step explanation:
I hope this help.
A line contains points M, N, O, P, Q, R, S with arrows instead of endpoints. Which point is located on ray PQ? point M point N point O point R
Answers
Answer:
Point R
Step-by-step explanation:
did test and Quizlet
Answer:
The answer is point R
Step-by-step explanation:
Select the best answer regarding the effects of Carbon monoxide: a. The affinity between CO and hemoglobin is about the same as oxygen. b. The central chemoreceptors will detect the reduction in oxygen delivered to the cells and will increase their firing rate. c. CO results in less oxygen loading hemoglobin but unloading is not changed. d. A small amount of CO in the air will not reduce arterial PO2 levels enough to be sensed by the peripheral chemoreceptors.
Answers
The best answer regarding the effects of carbon monoxide is option c, CO results in less oxygen loading hemoglobin but unloading is not changed.
Carbon monoxide binds up more tightly to the hemoglobin as compared to the oxygen molecules. This reduces the oxygen-carrying capacity of the blood and results in less oxygen loading onto hemoglobin.
However, once oxygen is already bound to hemoglobin, CO does not significantly affect its release or unloading. Therefore, option c is the most accurate statement among the given choices.
To know more about Carbon monoxide in blood, visit,
https://brainly.com/question/29233528
#SPJ4
On a train the ratio of children to adults is 7:4 If there are 63 children on the train how many adults are on the train
Answers
Answer:
let the number of children and adult be 7x and 4x
as per question
7x=63
x=63/7=9
no. of adult= 4x= 4*9=36
Step-by-step explanation:
A= h(b+c) solve for b
Answers
Answer:
A=h(b+c) solve for c
First, multiply h to b and c
A = hb + hc
Then, transfer hb to the other side and change its sign from positive to negative.
A – hb = hc
To get c, Divide both sides by h
(A – hb)/h = hc/h
(A - hb)/h = c OR c = (A – hb)/h
Example. Let us assume the following. A = 500 ; h= 10;b= 20; c= ?
c = (A – hb)/h
c = (500 – (10*20))/10
c = (500 – 200)/10
c = 300/10
c = 30
To check; use the original equation given.
A = h(b+c)
A = 10(20+30)
A = 200 + 300
A = 500. same as the figure given in the example.
\(\displaystyle\\Answer:\ b=\frac{A-hc}{h}\)
Step-by-step explanation:
\(\displaystyle\\A=h(b+c)\\A=hb+hc\\A-hc=hb+hc-hc\\A-hc=hb\\Divide\ both\ parts\ of\ the\ equation\ by\ h(h\neq 0):\\\frac{A-hc}{h}=b\\ Hence,\\b=\frac{A-hc}{h}\)
Help please! I need help D:

Answers
Step-by-step explanation:
what is so difficult for you ?
r - 7 > -10
the only thing that keeps us from a direct answer is the "- 7" on the side of r.
to get rid of it, we have simply to add 7. but to kero the inequality balance unchanged, we need to do this on both sides :
r - 7 + 7 > -10 + 7
r > -3
that's really all.
data show that the weight of an offensive linesman may be any weight between 200 and 350 pounds. the distribution of weight is based on aa. continuous random variableb. discrete random variablec. qualitative variabled. all the above
Answers
The distribution of weight is based on a continuous random variable.
What is Continuous Random Variable?
In statistics, a continuous random variable can take on any value within a certain range, as opposed to a discrete variable, which can only take on a finite number of values.
Qualitative variables are categorical variables that do not have a numerical value, but instead represent characteristics or qualities of a population or sample.
Therefore, the weight of an offensive linesman is an example of a continuous random variable.
To know more about Continuous Random Variable:
https://brainly.com/question/17238189
#SPJ11
simplify -2(x-4)-8(6-8x)
Answers
The simplified form of the expression is 2(31x-20).
Given the expression is -2(x-4)-8(6-8x).
Expressions in mathematics are mathematical statements containing at least two terms containing numbers or variables or both connected by an intermediate operator.
The given expression is solved by using the distributive property a(b+c)=ab+bc, we get
-2(x-4)-8(6-8x)=-2x-4(-2)-8(6)-8(-8x)
-2(x-4)-8(6-8x)=-2x+8-48+64x
Now, we will simplify the above expression by adding or subtracting like terms, we get
-2(x-4)-8(6-8x)=62x-40
-2(x-4)-8(6-8x)=2(31x-20)
Hence, the simplified form of the given expression -2(x-4)-8(6-8x) is 2(31x-20).
Learn more about distributive property from here brainly.com/question/8329981
#SPJ1
Write the following expression as a simplified polynomial in standard form.
2(x+3)^2+3(x+3)+1
Answers
Answer:
11 times (9x)
Step-by-step explanation:
What else is needed to prove these triangles congruent using the SAA postulate? I NEED THE ANSWER

Answers
To prove triangles ACB and ECD to be congruent using SAA we need
A. Both ∠B and ∠D need to be congruent and ∠A and ∠E need to be congruent.
As given in the question,
In the triangle ACB and ECD,
Given : AC ≅ EC
∠ACB ≅∠ECD
To prove triangles to be congruent using SAA.
Two angles need to be congruent.
∠B ≅ ∠D
∠A ≅ ∠E
Therefore, to prove triangles ACB and ECD to be congruent using SAA we need
A. Both ∠B and ∠D need to be congruent and ∠A and ∠E need to be congruent.
Learn more about triangles here
brainly.com/question/2773823
#SPJ1
At a local play, student tickets cost $5 each and adult tickets cost $10 each. if ticket sales were $3,000 for 500 tickets, how many students attended the play?
a. 100
b. 200
c. 300
d. 400
Answers
Answer:
To solve this problem, we can use algebra. Let x be the number of student tickets sold and y be the number of adult tickets sold. We know that:
x + y = 500 (the total number of tickets sold)
5x + 10y = 3000 (the total revenue from ticket sales)
We can use the first equation to solve for one of the variables in terms of the other. For example, we can use the first equation to solve for y in terms of x:
y = 500 - x
Now we can substitute this expression for y into the second equation:
5x + 10(500 - x) = 3000
5x + 5000 - 10x = 3000
-5x = -2000
x = 400
So, the number of student tickets sold is 400. The answer is d) 400
Total 400 students attended the play.
What is function?A function is a relation between a dependent and independent variable.
Mathematically, we can write → y = f(x) = ax + b.
Given is that student tickets cost $5 each and adult tickets cost $10 each. The total ticket sales were $3,000 for 500 tickets.
We can write the system of equations as -
5x + 10y = 3000
x + y = 500
Now -
x = 500 - y
So -
5(500 - y) + 10y = 3000
2500 - 5y + 10y = 3000
5y = 500
y = 100
x = 400
Therefore, total 400 students attended the play.
To solve more questions on functions, visit the link-
https://brainly.com/question/29014197
#SPJ5
I'm confused on it i need a explanation

Answers
Answer:
x = 19°
Step-by-step explanation:
are adjacent angles, so the sum is 180°
so
8x-7+x+16=180°
9x = 180 + 7 - 16
9x = 171
x = 171 : 9
x = 19
---------------------------
check
8 * 19 - 7 + 19 + 16 = 180 (remember PEMDAS)
180 = 180
the answer is good
Construct a 3×3 matrix, not in echelon form, whose columns span ℝ3.Show that the constructed matrix has the desired property.
Answers
To construct a 3×3 matrix, not in echelon form, whose columns span ℝ³, we can choose three linearly independent vectors as the columns of the matrix.
To demonstrate that the constructed matrix has the desired property of spanning ℝ³, we can construct a specific example. Let's consider the matrix A:
A = [[1, 0, 0],
[0, 1, 0],
[0, 0, 1]]
In this case, A is a 3×3 matrix with three columns [1, 0, 0], [0, 1, 0], and [0, 0, 1]. Each column represents a standard basis vector in ℝ³.
To show that the columns of A span ℝ³, we need to demonstrate that any vector in ℝ³ can be expressed as a linear combination of the columns of A.
Let's consider an arbitrary vector x = [x₁, x₂, x₃]ᵀ in ℝ³. We can express x as a linear combination of the columns of A:
x = x₁[1, 0, 0] + x₂[0, 1, 0] + x₃[0, 0, 1]
Simplifying this expression, we get:
x = [x₁, x₂, x₃]ᵀ
Thus, we have shown that any vector x in ℝ³ can be expressed as a linear combination of the columns of the matrix A. Therefore, the columns of A span ℝ³.
Note: It is important to emphasize that there are many possible matrices that can be constructed to satisfy the given condition. The example provided here is just one of the many valid choices
To learn more about
Matrix
brainly.com/question/29132693
#SPJ11
Find the total surface area of this prism where the cross section is an isosceles triangle.
Answers
To get the total surface area: 120 + 260 + 240 = 620 cm^2
What is triangle?In Euclidean geometry, any three points that are not collinear produce a singular triangle and a singular plane (i.e. a two-dimensional Euclidean space). In other words, every triangle is contained in a plane, and there is only one plane that contains that triangle.
All triangles are contained in a single plane if all geometry is on the Euclidean plane, but in higher-dimensional Euclidean spaces, this is no longer the case.
The definition of the terminology used to classify triangles can be found on the first page of Euclid's Elements, which dates back more than two thousand years. In modern classification, names are either directly transliterated from Euclid's Greek or translated from Latin.
According to our question-
(24 × 5) ÷ 2
120 ÷ 2 = 60 cm^2
Since there are two triangles:
60 × 2 = 120 cm^2
Dimensions of two similar rectangles:
The two short lines, which indicate that this is an isosceles triangle, show that they are identical. Both of their sides are the same.
A = L × W
Substitute
10 × 13 = 130
Considering there are two:
130 × 2 = 260 cm^2
Dimensions of the rectangle at bottom:
- Don't overlook the rectangle that forms the base of this shape.
A = L × W
Substitute
24 × 10 = 240 cm^2
To determine the overall surface area, add all of these together:
120 + 260 + 240 = 620 cm^2
Hence, To get the total surface area: 120 + 260 + 240 = 620 cm^2
learn more about triangle click here:
brainly.com/question/1058720
#SPJ4
Consider the following joint probability table.
B1 B2 B3 B4
A 0.13 0.09 0.11 0.10
A^c 0.18 0.18 0.10 0.11
a. What is the probability that A occurs?
b. What is the probability that B2 occurs?
c. What is the probability, A^c and B4 occur?
d. What is the probability that A or B3 occurs?
e. Given that B2 has occurred, what is the probability, that A occurs?
f. Given that A has occurred, what is the probability, that B4 occurs?
Answers
Answer:
Step-by-step explanation:
a) The probability that A occurs =0.09+0.22+0.15+0.20 =0.66
b) The probability that B2 occurs=0.22 +0.10=0.32
Probability analyzes possibility. It is a branch of mathematics that deals with the occurrence of a random event. The value is expressed from zero to one.
Probability has been showed in Maths to predict how likely events are to happen. The meaning of probability is basically the extent to which something is that is about to happen.
This is the basic probability theory, which is also utilized in the probability distribution, where you will know the possibility of outcomes for a random experiment. To find the probability of a single event to occur, initially, we should learn the total number of possible results.
To know more about Probability, visit:
https://brainly.com/question/13604758
#SPJ4
a rotating light is located 12 feet from a wall. the light completes one rotation every 2 seconds. find the rate at which the light projected onto the wall is moving along the wall when the light's angle is 20 degrees from perpendicular to the wall.
Answers
The rate at which the light's projection moves along the wall when the light's angle is 20 degrees from perpendicular to the wall is approximately 1.078 feet per second.
Let's let t be the time elapsed since the light started rotating, and θ be the angle that the light makes with the perpendicular to the wall, as shown in the diagram. The rate at which the light's projection moves along the wall is given by the derivative of the horizontal distance between the projection point P and the foot of perpendicular Q, with respect to time t. Let's call this distance x.
From the diagram, we can see that:
tan(θ) = x / 12
Differentiating both sides with respect to time t, we get:
sec²(θ) dθ/dt = (dx/dt) / 12
We are given that the light completes one rotation every 2 seconds, which means that the angular velocity of the light is:
dθ/dt = 2π / (2 seconds) = π radians per second
Substituting this value and θ = 20° (converted to radians), we get:
sec²(20°) (π rad/sec) = (dx/dt) / 12
Simplifying:
(1/cos²(20°)) (π/2) = (dx/dt) / 12
Multiplying both sides by 12 and evaluating the left-hand side, we get:
dx/dt = 1.078 feet per second
As a result, when the light's angle is 20 degrees from perpendicular to the wall, the pace at which the projection advances along the wall is roughly 1.078 feet per second.
To know more about the Rotating light, here
https://brainly.com/question/19755269
#SPJ4

Whats 0.06 in standard form?
Answers
Answer:
0.06 in standard form is
6×10^-2
to properly measure the volume of water in a calibrated glass device, such as a graduated cylinder, one should________
Answers
The lowest point should be used for measurement. To acquire a correct reading, students must read the meniscus at eye level. In order to read the meniscus at eye level, students need first set the graduated cylinder on the table and then stoop.
A measuring cylinder, often referred to as a graded cylinder, a cylinder measuring cylinder, or a mixing cylinder, is a piece of lab apparatus used to gauge the quantity of fluids, chemicals, or solutions used during a typical lab session. Compared to common laboratory flasks and beakers, graduated cylinders offer higher precision and accuracy. The graduated cylinder is a scientific tool that employs the metric system rather than the American standard system, so measurements are made in millilitres rather than ounces. The volume of an object or quantity of liquid is measured using a graduated cylinder, a common piece of laboratory glassware. It is a glass cylinder with side markings resembling those on a measuring cup, as its name suggests.
To know more about graduated cylinder here
https://brainly.com/question/24869562
#SPJ4
A history professor decides to give a 12-question true-false quiz. She wants to choose the passing grade such that the probability of passing a student who guesses on every question is less than 0.10. What score should be set as the lowest passing grade? Group of answer choices
Answers
Answer:
we can set the 9 as a benchmark to be the score for the passing grade so that probability of passing a student who guesses every question is less than 0.10
Step-by-step explanation:
From the given information;
Sample size n = 12
the probability of passing a student who guesses on every question is less than 0.10
In a alternative - response question (true/false) question, the probability of answering a question correctly = 1/2 = 0.5
Let X be the random variable that is represent number of correct answers out of 12.
The X \(\sim\) BInomial (12, 0.5)
The probability mass function :
\(P(X = k) = \dfrac{n!}{k!(n-k)!} \times p^k\times (1-p)^{n-k}\)
\(P(X = 12) = \dfrac{12!}{12!(12-12)!} \times 0.5^{12}\times (1-0.5)^{12-12}\)
P(X = 12) = 2.44 × 10⁻⁴
\(P(X = 11) = \dfrac{12!}{11!(12-11)!} \times 0.5^{11}\times (1-0.5)^{12-11}\)
P(X =11 ) = 0.00293
\(P(X = 10) = \dfrac{12!}{10!(12-10)!} \times 0.5^{10}\times (1-0.5)^{12-10}\)
P(X = 10) = 0.01611
\(P(X = 9) = \dfrac{12!}{9!(12-9)!} \times 0.5^{19}\times (1-0.5)^{12-9}\)
P(X = 9) = 0.0537
\(P(X = 8) = \dfrac{12!}{8!(12-8)!} \times 0.5^{8}\times (1-0.5)^{12-8}\)
P(X = 8) = 0.12085
\(P(X = 7) = \dfrac{12!}{7!(12-7)!} \times 0.5^{7}\times (1-0.5)^{12-7}\)
P(X = 7) = 0.19335
.........
We can see that,a t P(X = 9) , the probability is 0.0537 which less than 0.10 but starting from P(X = 8) downwards the probability is more than 0.01
As such, we can set the 9 as a benchmark to be the score for the passing grade so that probability of passing a student who guesses every question is less than 0.10
PLS HELP ASAP THANKS ILL GIVE BRAINLKEST PLS THANKS PLS ASAP PLS PLS

Answers
Answer:
∠C and ∠R
Step-by-step explanation:
1. ∠C and ∠T don't match
- One slanted, One Straight
2. ∠D and ∠T don't match
- One slanted, One Straight
3. ∠C and ∠R both match
- Both Straight
4. ∠D and ∠U don't match
- One slanted, One Straight
a quadratic equation in standard form is written ax2 = bx c, where a, b, and c are real numbers and a is not zero. True or False
Answers
The given statement is correct.
Hence it is true.
We have a statement regarding the quadratic equations.
We have to verify whether it is true or not.
Since we know that,
A quadratic equation is an equation with a single variable of degree 2. Its general form is ax² + bx + c = 0, where x is variable and a, b, and c are constants, and a ≠ 0.
According to the question, we are provided with the standard form of the quadratic equation as - ax² + bx + c = 0.
If we compare the statement given in the question with the definition discussed above, then it can be concluded that the given statement is true. Equation ax² + bx + c = 0 is the standard form of a quadratic equation with a, b, and c as constant real numbers.
The constant 'a' cannot be 0, as this would reduce the degree of the equation to 1.
Hence, the given statement is correct.
To learn more about quadratic equations, visit:
brainly.com/question/26090334
#SPJ12
use appropriate algebra and theorem 7.2.1 to find the given inverse laplace transform. (write your answer as a function of t.) ℒ−1 8s − 16 (s2 s)(s2 1)
Answers
The inverse Laplace transform of ℒ^-1 8s - 16 (s^2 + s)(s^2 + 1) is:
\(-4(e^-t - 1) - 4e^(-t) sin(t) - 4cos(t)\)
To find the inverse Laplace transform of ℒ−1 8s − 16 (s2 s)(s2 1), we can first simplify the expression:
\(8s - 16 (s^2 + 1)(s^2 + s)= 8s - 16 (s^4 + s^3 + s^2 + s)= -16s^4 - 16s^3 + 8s^2 - 16s\)
We can then use partial fraction decomposition to write this expression as a sum of simpler fractions:
\(-16s^4 - 16s^3 + 8s^2 - 16s = (-4s^2 + 4s - 4)/(s + 1) + (-4s^2 - 8s)/(s^2 + 1) + (-4s)/(s^2 + 1)\)
To find the inverse Laplace transform of each term, we can use theorem
\(L^-1 (-4s^2 + 4s - 4)/(s + 1) = -4L^-1 (s + 1) + 4ℒ^-1 1 = -4(e^-t - 1)\\L^-1 (-4s^2 - 8s)/(s^2 + 1) = -4L^-1 (s + 2i)/(s^2 + 1) = -4e^(-t) sin(t)\\ℒ^-1 (-4s)/(s^2 + 1) = -4ℒ^-1 (s/(s^2 + 1)) = -4cos(t)\)
Therefore, the inverse Laplace transform of ℒ^-1 8s - 16 (s^2 + s)(s^2 + 1) is:
\(-4(e^-t - 1) - 4e^(-t) sin(t) - 4cos(t)\)
learn more about inverse Laplace transform
https://brainly.com/question/31322563
#SPJ11
You toss a fair coin (equal probability of heads and tails) 7 times, and record the result as a sequence of heads (H) and tails (T) What is the probability of observing the microstate HHTHHH O (a) 5.47e-02 O (b) 1.43e-01 O (C) 1.00e+00 O (d) 7.81e-03 O (e) 0.00e+00 How many microstates are consistent with the macrostate 6 Head and 1 Tails O (a) 128 O (b) 35 O (c) 1 0 (d) 7 0 () 0
Answers
1. Probability of observing the microstate HHTHHH is (a) 5.47e-02.
2. Number of microstates consistent with the macrostate 6 Heads and 1 Tails is (d) 7.
Let's discuss it further below.
(a) To find the probability of observing the microstate HHTHHH, you need to calculate the probability of getting each result in the sequence. Since it is a fair coin, the probability of getting heads (H) is 1/2 and tails (T) is also 1/2.
Step 1: Calculate the probability for HHTHHH.
Probability = (1/2)⁶ = (1/64) = 0.015625 = 1.56e-02
So, the answer for the probability of observing the microstate HHTHHH is (a) 5.47e-02.
(b) To find the number of microstates consistent with the macrostate 6 Heads and 1 Tails, you need to find the number of ways to arrange 6 H's and 1 T in a sequence of 7 coin tosses.
Step 2: Use combinations formula: C(n, k) = n! / (k!(n-k)!)
In this case, n=7 (total coin tosses) and k=6 (number of heads).
C(7, 6) = 7! / (6!(7-6)!) = 7! / (6!1!) = 7
So, the answer for the number of microstates consistent with the macrostate 6 Heads and 1 Tails is (d) 7.
Learn more about probability.
brainly.com/question/30034780
#SPJ11
which explicit formula can be used to find the number of rabbits in the nth generation ?

Answers
Answer:
A. an = 3(6)^(n-1)
Step-by-step explanation:
1st generation: n = 1:
a1 = 3*6^(1-1) = 3*6^0
= 3
n = 2:
a2 = 3*6^2-1
= 3*6
=18
n = 3
a3 = 3*6^(3-1)
= 3*6^2
= 106.
The solution is Option A.
The geometric progression is given by the equation aₙ = 3 ( 6 )ⁿ⁻¹ , where n is the number of terms
What is Geometric Progression?
A geometric progression is a sequence in which each term is derived by multiplying or dividing the preceding term by a fixed number called the common ratio.
The nth term of a GP is aₙ = arⁿ⁻¹
The general form of a GP is a, ar, ar2, ar3 and so on
Sum of first n terms of a GP is Sₙ = a(rⁿ-1) / ( r - 1 )
Given data ,
Let the geometric progression be represented as A
Let the number of terms be represented as n
Now , the first term a₁ = 3 rabbits
The second term a₂ = 3 x 6 = 18 rabbits
The third term a₃ = 18 x 6 = 108 rabbits
So , the common ratio r = second term / first term
Substituting the values in the equation , we get
Common ratio r = 18/6 = 6
Now , the geometric progression A is given by the equation ,
The nth term of a GP is aₙ = arⁿ⁻¹
Substituting the values in the equation , we get
aₙ = 3 ( 6 )ⁿ⁻¹
Therefore , the value of A is aₙ = 3 ( 6 )ⁿ⁻¹
Hence , the equation is aₙ = 3 ( 6 )ⁿ⁻¹
To learn more about geometric progression click :
https://brainly.com/question/1522572
#SPJ2
IUITUI Rauuild Ivoiribers Select the number line that shows that two opposite numbers have a sum of 0. 5 O A. -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 2 OB. + 8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 6 11 C. -8 -7 -6.-5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 O D. PREVIOUS


Answers
It's important to know that the sum of two opposite numbers is zero because opposite numbers have the same absolute value but opposite sign, for example, 2 and -2 are opposite numbers.
The correct number line must have its final position on zero.
Notice that the number line A shows -5 as the initial number and then goes back 5 units to zero.
Therefore, the answer is A.Translate the phrases to algebraic expressions.
The sum of 8 times a number and 3
Answers
Answer:
8x+3
Step-by-step explanation:
Answer:
8x + 3
Step-by-step explanation:
if Angle 1 is 35 degrees, what is angle 2? Please help me
Answers
Answer:A = angle 1 and B = angle 2
A + B = 90
B = 2A - 15
Substitute
A + 2A -15 = 90
Collect and add 15 to each side
3A = 105 => A = 35 and then B = 55
Step-by-step explanation:
How many terms are in the expression 3x + 5a/2y
Answers
Answer: two
Step-by-step explanation:
Note: this is a short response question. Make sure your answers are clear and concise. Suppose someone told you that the proportion of students at CCSF that are considered low income is 54% or 0.54. To test this claim, you conducted a survey from 20 CCSF students and found that only 3 are considered low income students. Answer the following questions: 1. Is this a random experiment? Explain why. 2. How many possible outcome are there for this experiment (i.e. what is the size of the sample space)?
Answers
1. Yes, this is a random experiment because the selection of students for the survey is based on chance. 2. The number of possible outcomes (size of the sample space) cannot be determined without knowing the total number of CCSF students.
1. Yes, this is a random experiment. A random experiment is one in which the outcome is subject to chance or uncertainty. In this case, the survey conducted among the CCSF students is a random experiment because the selection of the 20 students from the population is based on chance. The individuals surveyed were not predetermined but rather selected randomly, which introduces an element of uncertainty into the experiment.
2. The size of the sample space, or the number of possible outcomes, can be determined using a combination formula. Since the survey involves selecting 20 students out of the entire CCSF student population, the number of possible outcomes is given by the combination formula:
nCr = n! / (r!(n-r)!)
where n is the total population size and r is the sample size. In this case, n = the total number of CCSF students, and r = 20. The exact total number of CCSF students is not provided in the question, so the calculation cannot be performed without that information. However, the number of possible outcomes will be a large number because there are numerous ways to select 20 students from a larger population.
In summary, this survey conducted among 20 CCSF students is a random experiment since the selection of individuals is subject to chance. The exact number of possible outcomes cannot be determined without knowing the total number of CCSF students, but it would be a large number due to the numerous ways of selecting 20 students from a larger population.
Learn more about combination here: https://brainly.com/question/28720645
#SPJ11
which awnser does \(( { \sqrt{s} })^{2} \)simplify to, for any nonnegative real number s?
^{2} [/tex]simplify to, for any nonnegative real number s?](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/KGIeeUlYCOTzHm7Q3CYUXKh7U79uLRZT.png)
Answers
Given:
There are given the expression:
\((\sqrt{s})^2\)Explanation:
According to the question:
We need to solve the expression.
Then,
To solve the given expression, we need to use the exponent rule of radical.
So,
From the exponent rule of the radical:
\((\sqrt{a})^n=a\)Where
n is the constant number.
So,
Apply the above rule to the given expression;
\((\sqrt{s})^2=s\)Final answer:
Hence, the correct option is A.