The average height of BYU freshman from a random sample of 450 freshman at BYU is 68 inches with a standard deviation of 1.5 inches. What is the 98% confidence interval for the average height of BYU freshman?
a. (59.86, 60.14)
b. (67.83, 68.17)
c. (66.5. 69.5)
d. (67.86, 68.14)
Answers
Answer:
b. (67.83, 68.17)
Step-by-step explanation:
We have that to find our \(\alpha\) level, that is the subtraction of 1 by the confidence interval divided by 2. So:
\(\alpha = \frac{1 - 0.98}{2} = 0.01\)
Now, we have to find z in the Z-table as such z has a p-value of \(1 - \alpha\).
That is z with a pvalue of \(1 - 0.01 = 0.99\), so Z = 2.327.
Now, find the margin of error M as such
\(M = z\frac{\sigma}{\sqrt{n}}\)
In which \(\sigma\) is the standard deviation of the population and n is the size of the sample.
\(M = 2.327\frac{1.5}{\sqrt{450}} = 0.17\)
The lower end of the interval is the sample mean subtracted by M. So it is 68 - 0.17 = 67.83.
The upper end of the interval is the sample mean added to M. So it is 68 + 0.17 = 68.17.
This means that the correct answer is given by option B.
Related Questions
Find the measure of each angle in the following triangle
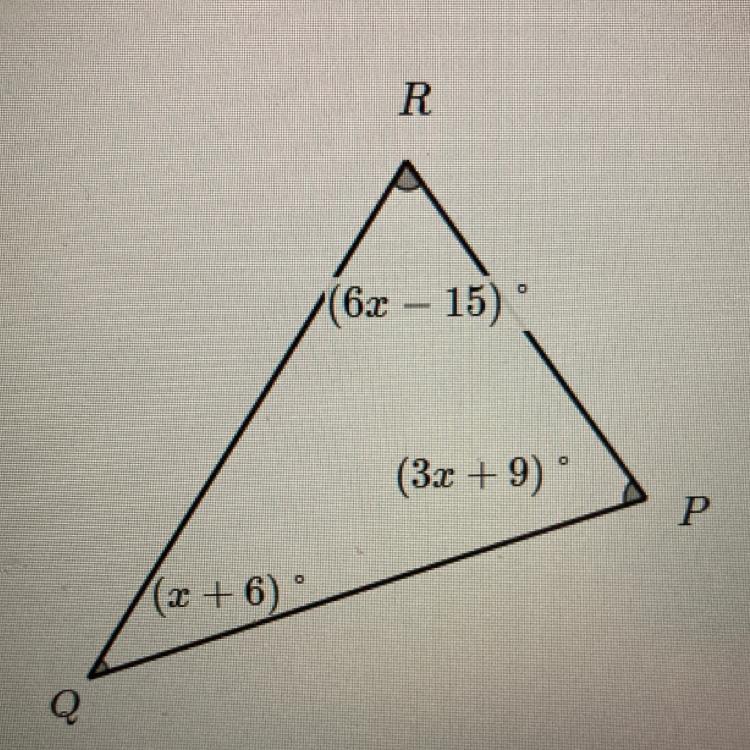
Answers
all the angles should add up to 180
6x-15+3x+9+x+6=180
move 6, 9 and -15 to 180 side
6x+3x+1x=180
add 6x+3x+1x
10x=180
180/10= 18
x is 18
R=6(18)-15 = 93
P=3(18)+9 = 63
Q=18+6 = 24
double check:
93+63+24= 180
URGENT!! ILL GIVE BRAINLIEST!!!! AND 100 POINTS!!!

Answers
The value of x that will make the two given solids similar is: d. x = 31.
What are the Dimensions of Similar Solids?If two solids are said to be similar to each other, it means that one is a scale copy of the other, and one is enlarged by a scale factor to get the dimension of the other.
Thus, the corresponding linear dimensions of two similar solids are proportional or they have equal ratio.
Based on this definition, the equation below would be created to find the value of x that would make both solids similar to each other.
29/14.5 = x/15.5
Cross multiply:
14.5x = (15.5)(29)
14.5x = 449.5
14.5x/14.5 = 449.5/14.5
x = 31.
Learn more about similar solids on:
https://brainly.com/question/16599646
#SPJ1
A regular octagon has a side length of 7 inches.
a. How many sides does an octagon have?
b. Find its perimeter.
a. An octagon has 8 sides.
b. The perimeter is _____
inches.
Answers
Solve for n. 7n - 2 = 5n + 6
Answers
Answer:
n = 4
Step-by-step explanation:
Pre-SolvingWe are given the equation 7n - 2 = 5n + 6, ans we want to solve it for n.
To do this, we need to isolate n one one side.
SolvingLet's start by adding 2 to both sides.
7n - 2 = 5n + 6
+2 +2
_______________
7n = 5n + 8
Now, subtract 5n from both sides.
7n = 5n + 8
-5n -5n
_______________
2n = 8
Divide both sides by 8 to get the value of n.
2n = 8
÷2 ÷2
________
n = 4
Solve the equation by first subtracting 2/3 from each side
3x + 2/3 =7 5/6
Answers
The solution to the equation is x = 2 7/18
How to determine the solution to the equationFrom the question, we have the following parameters that can be used in our computation:
3x + 2/3 =7 5/6
Solve the equation by first subtracting 2/3 from each side
So, we have
3x = 7 1/6
Divide both sides of the equation by 3
This gives
x = 2 7/18
Hence, the solution is 2 7/18
Read more about equation at
https://brainly.com/question/2972832
#SPJ1
If
to DEF?
A 23
B. 16°
C. 32°
D. 58°
Answers
The calculated measure of the angle D is (c) 32 degrees
How to determine the measure of the angleFrom the question, we have the following parameters that can be used in our computation:
The triangles ABC and DEF
The triangles are similar triangles
This means that the corresponding angles are equal
Given that
A = 32 degrees
And the corresponding angle is D
We have
D = 32 degrees
Hence, the measure of the angle is (c) 32 degrees
Read more about angles at
https://brainly.com/question/31898235
#SPJ1

Are the ratios 6:3 and 4:2 equivalent
Answers
Determine whether each of the following provides enough information to prove that △SQP ≅ △SQR. Select Yes or No for each statement.
Q is the midpoint of PR.
∠P ≅ ∠R
∠SQP is a right angle, ∠PSQ ≅ ∠RSQ
∠SQP is a right angle, m∠P = 33°, m∠RSQ = 57°
∠P ≅ ∠R, ∠PSQ ≅ ∠RSQ
Answers
For each statement for triangle SQP and SQR, Q is the midpoint of PR: No, ∠P ≅ ∠R: No, ∠PSQ ≅ ∠RSQ: Yes, m∠P = 33°, m∠RSQ = 57°: No, ∠P ≅ ∠R, ∠PSQ ≅ ∠RSQ: Yes.
What is triangle?
A triangle is a geometric shape that consists of three line segments connected end-to-end to form a closed shape. Triangles are one of the basic shapes studied in geometry and are used in a wide range of applications, from construction to computer graphics.
Here are the answers to whether each statement provides enough information to prove that △SQP ≅ △SQR:
Q is the midpoint of PR: No, this information alone is not sufficient to prove the triangles are congruent. We need additional information about the angles or sides.
∠P ≅ ∠R: No, this information alone is not sufficient to prove the triangles are congruent. We need additional information about the sides or other angles.
∠SQP is a right angle, ∠PSQ ≅ ∠RSQ: Yes, this information is sufficient to prove that the triangles are congruent by the angle-angle-side (AAS) congruence criterion.
∠SQP is a right angle, m∠P = 33°, m∠RSQ = 57°: No, this information alone is not sufficient to prove the triangles are congruent. We need additional information about the sides or other angles.
∠P ≅ ∠R, ∠PSQ ≅ ∠RSQ: Yes, this information is sufficient to prove that the triangles are congruent by the angle-angle-angle (AAA) congruence criterion.
To learn more about triangle visit:
https://brainly.com/question/17335144
#SPJ1
Four wires (red,green, blue and yellow) need to be attached to a circuit board. A robotic device will attach the wires. The wires can be attached in any order, and the production manager wishes to determnine which order would be the fastest for the robot to use.
Required:
Use the multiplication rule of counting to determine four choices for the first wire, three for the second wire, two for the third and only one for the fourth.
Answers
Answer:
24
Step-by-step explanation:
The topic here is COMBINATORICS.
The parent topic is PERMUTATIONS & COMBINATORICS.
Permutation deals with arrangement in a definite order while, as stated in the question here, definite order in not needed in Combinatorics.
Now, the multiplication rule of counting, also known as the rule of product, talks about the multiplication of the figures that represent the different ways of doing something.
For example, in this question, the robot needs to attach 4 wires to a circuit board. If you know how Physics or Electricity works, you'll that truly this is a combination matter and not permutation.
Putting/Connecting the 4 wires together (in a square shaped circuit for instance), the arrangement RGBY is different from RGYB or RBGY.
So there will be more ways to connect or combine these wires, than if we were to follow a definite rule like: "Red and Green must always stay together".
So using the multiplication rule of counting to determine 4 choices for the Red wire, 3 choices for the Green wire, 2 choices for the Blue wire, and 1 choice for the yellow wire, we have:
R4 x G3 x B2 x Y1 = 4 x 3 x 2 x 1 = 4! = 24
The term "4!" means "Four Factorial".
Divide. Express your answer in simplest form.
2 1/2 divided by 2 1/6
Answers
Answer:
15/13
Step-by-step explanation:
Convert to improper fractions: 5/2 divided by 13/6
Multiply the first term by reciprocal: 5/2 * 6/13 = 30/26
Simplify: 30/26 can become 15/13
\( = 2 \frac{1}{2} \div 2 \frac{1}{6} \)
\( = \frac{5}{2} \div \frac{13}{6} \)
\( = \frac{5}{2} \times \frac{6}{13} \)
\( = \frac{30}{26} \)
\( = \frac{30 \div 2}{26 \div 2} \)
\( = \frac{15}{13} \)
\(\color{hotpink} = 1 \frac{2}{13} \)
\(\therefore\color{olive}2 \frac{1}{2} \div 2 \frac{1}{6} = \color{hotpink} \frac{15}{13}\color{olive} (or) \color{hotpink}1\frac{2}{3} \)
Which number set correctly represents the range of the given data?
{(0, 0), (2, 0), (3, 0), (5, 0)}
{0, 2, 3,5)
{0, 2, 3)
{0,2)
(0)
Answers
Answer:
I would assume {0, 2, 3, 5}
Step-by-step explanation:
I would assume that answer because all three are given in the range of the given data set.
Answer:
The answer is [0] (D)
Step-by-step explanation:
Given the fact that the Range is Y value, we see 0,0,0,0
So its 0
y=3x+2
y=3x−6
how many solutions does the system have
Answers
Answer:
no solutions
Step-by-step explanation:
The lines are parallel since they have the same slope
y = mx+b where m is the slope
They have different y intercepts (b)
The will never intersect so they have no solutions
find the difference between 0.1 kg and 75g
Answers
Answer:
25 g
Step-by-step explanation:
0.1 kg can be written as 100 grams
& 75 g
while 1 kg is 1000 grams
so difference:-
(100- 75 ) grams
= 25 g
The difference between 0.1 kg and 75 g is 25 grams. To find the difference between 0.1 kg and 75g, you need to make sure both quantities have the same unit.
Since 1 kg is equal to 1000 g, you can convert 0.1 kg to grams:
0.1 kg = 0.1 * 1000 g = 100 g
Now, the two quantities are in the same unit:
0.1 kg - 75 g = 100 g - 75 g = 25 g
So, the difference between 0.1 kg and 75 g is 25 grams.
To know more about difference:
https://brainly.com/question/30241588
#SPJ2
What is the northerly Component of a wind blowing at 15ms from the South East?
Answers
The northerly component of the wind blowing at 15 m/s from the South East is approximately 10.605 m/s.
To determine the northerly component of a wind blowing from the South East, we need to consider the direction from which the wind is coming and its magnitude.
A wind blowing from the South East means it is coming from the South East direction towards the opposite direction, which is the North West. Since the wind is coming from the South East, we can say it has a southeasterly direction.
To find the northerly component, we need to break down the wind vector into its north and east components. The northerly component represents the part of the wind that is directed towards the north.
If we assume that the wind is blowing at an angle of 45 degrees with respect to the North, we can use trigonometry to find the components. Since the wind is blowing at 15 m/s, we can consider it as the hypotenuse of a right triangle.
The northerly component can be found using the sine of the angle:
Northerly Component = Wind Speed * sin(Angle)
Northerly Component = 15 m/s * sin(45°)
Using the value of sin(45°) (which is √2 / 2 ≈ 0.707), we can calculate the northerly component:
Northerly Component ≈ 15 m/s * 0.707
Northerly Component ≈ 10.605 m/s
For more such questions on northerly component
https://brainly.com/question/2926396
#SPJ8
En una ciudad de 5000 habitantes, la tasa diaria
de infección con un virus de la gripe varia directamente con el producto de
personas infectadas y el número de personas no infectadas. Cuando se han
infectado 1000 personas, la gripe se esparce a razón de 40 nuevos casos por día.
¿Para qué número de personas infectadas, la tasa diaria de infección es la
máxima?
Answers
According to the information, the maximum infection rate is: k * 2500 * (5000 - 2500) = 6250k = 40
How to calculate for what number of infected people, the daily infection rate is the maximum?To address this problem, we can use the law of the infection rate, which states that the infection rate is directly proportional to the product of the number of people infected and the number of people not infected. Therefore, we can write:
infection rate = k * (infected people) * (uninfected people)where "k" is a constant of proportionality. Since we want to find the number of people infected that produces the maximum infection rate, we can consider the infection rate as a function of the variable "x" representing the number of people infected. Therefore, we can write:
infection rate = k * x * (5000 - x)To find the value of "x" that maximizes the infection rate, we can derive this function and set the derivative equal to zero:
d(infection rate)/dx = k * (5000 - 2x) = 0This implies that 5000 - 2x = 0, and therefore:
x = 2500Therefore, the number of infected people that produces the maximum daily rate of infection is 2,500.
However, we must verify that this result is consistent with the information given in the problem. We know that when there are 1,000 people infected, the flu spreads at the rate of 40 new cases per day. Therefore, if we add 1,500 more infected people (for a total of 2,500), the infection rate would be:
infection rate = k * 2500 * (5000 - 2500) = 6250kIf the infection rate is 40 new cases per day, we have:
40 = 6250kwhich implies that:
k = 0.0064Therefore, the maximum infection rate is:
maximum infection rate = k * 2500 * (5000 - 2500) = 6250k = 40Learn more about infection in: https://brainly.com/question/29850356
#SPJ1
Which is a whole number?
0.86
2/5
98
35%
Answers
Answer:
98 is a whole number
Step-by-step explanation:
0.86 is a decimal
2/5 is a fraction
35% is a percentage
A bag contains 8 white marbles, 4 green marbles and 3 blue marbles. 2 marbles are selected at random without replacement, find the probability th
first marble is blue and the second marble is white, that is P(blue marble and white marble)
Answers
Answer:
24/225
Simplified: 8/75
Step-by-step explanation:
8 + 4 + 3 = 15
Since there are no replacements the denominator will get lower every time a marble is pulled.
First is blue which means,
3/15
The second is white,
8/15
If I'm not wrong you would multiply 3/15 and 8/15 and you get 24/225.
Simplified: 8/75
The probability that the first marble is blue and the second marble is white, that is P(blue marble and white marble) is 8/75.
What is the probability?Probability refers to a possibility that deals with the occurrence of random events. The probability of all the events occurring need to be 1.
The formula of probability is defined as the ratio of a number of favorable outcomes to the total number of outcomes.
A bag contains 8 white marbles, 4 green marbles and 3 blue marbles.
2 marbles are selected at random without replacement.
Total number of marbles
8 + 4 + 3 = 15
Since there are no replacements the denominator will get lower every time a marble is pulled.
The first marble is blue ; 3/15
The second is white ; 8/15
The probability that the first marble is blue and the second marble is white, that is P(blue marble and white marble)
= 3/15 x 8/15
= 24/225.
= 8/75
Learn more about probability here;
https://brainly.com/question/11234923
#SPJ2
Two parallel lines passing the vertices with red line r at points (c, d) at (2, 10) and (0, b) at (0, 6) and blue line s intercepts (c, 0) at (2, 0) and (0, a) at (0, minus 4) Statements Reasons 1. given 2. application of the slope formula 3. distance from to equals the distance from to definition of parallel lines 4. application of the distance formula 5. substitution property of equality 6. inverse property of addition 7. substitution property of equality Which step of the proof contains an error? A. Step 5 B. Step 6 C. Step 2 D. Step 4
Answers
Answer:
transitive property
Step-by-step explanation:
Solve for x:
4(x-5)
8
= 9y
X =
= [?]y + []
Enter
![Solve for x:4(x-5)8= 9yX == [?]y + []Enter](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/LbASv4mWYxdYXFA9gVR2mLKk0jlXUpSF.png)
Answers
4x - 20 = 72y
4x - 72y = 20
4x = 20 + 72y
X = 20/4 + 72/4 y
X = 5 + 18y
Gary weighed 187 pounds after graduating
high school. 5 years later he weighs 228
pounds. By what percentage has his weight
changed?
Plz helppppppp
Answers
eat chili snacks and spicy to burn fat
PLEASE HELP ASAP
Consider the graph of the line y = 1/2x-4 and the point
(-4,2).
The slope of a line parallel to the given line is
A point on the line parallel to the given line, passing
through (-4, 2), is
The slope of a line perpendicular to the given line is
v.
A point on the line perpendicular to the given line,
passing through (-4, 2), is
1) Intra
-12
-8
14
8
-8
y
8
12

Answers
1) Parallel lines have the same slope, so the answer is 1/2
2) Perpendicular lines have slopes that are negative reciprocals, so the answer is -2
3) The equation of the perpendicular is y = -2x - 6, so a point is (0, -6)
find w + y + y + z
someone pls help

Answers
Answer:
300
Step-by-step explanation:
30+30+w+x+y+z = 360 (all angles round a point add up to 360)
Simplifying :
60 + w+x+y+z = 360
Subtracting 60 from both sides :
w+x+y+z = 300
Hope this helped and brainliest ?
Sum of entire angle=360°
so
30+x+y+x+w+30=360w+x+y+z=360-60w+x+y+z=300What is the value of the expression below when y=4y=4? 3y^2 +y+8 3y 2 +y+8
Answers
Answer:
1. 18
2. 13.5
3. 3rd choice
4. 2nd choice
5. 18.6
6.3m + 8
7. 5x2 + y
i hope this work for you
For each pair of functions f, g below, find f(g(x)) and g(f(x))
Then, determine whether and are inverses of each other.
Simplify your answers as much as possible.
(Assume that your expressions are defined for all in the domain of the composition.
You do not have to indicate the domain.)

Answers
Answer:
See below
Step-by-step explanation:
Part A
\(f(g(x))=f(\frac{x}{3})=3(\frac{x}{3})=x\\g(f(x))=g(3x)=\frac{3x}{3}=x\)
Since BOTH \(f(g(x))=x\) and \(g(f(x))=x\), then \(f\) and \(g\) are inverses of each other
Part B
\(f(g(x))=f(\frac{x+1}{2})=2(\frac{x+1}{2})+1=x+1+1=x+2\\g(f(x))=g(2x+1)=\frac{(2x+1)+1}{2}=\frac{2x+2}{2}=x+1\)
Since BOTH \(f(g(x))\neq x\) and \(g(f(x))\neq x\), then \(f\) and \(g\) are NOT inverses of each other
Solve the system by graphing :y=2x-3y=-x+9
Answers
Answer:
(4,5)
Explanation:
Given the system of equations:
\(\begin{gathered} y=2x-3 \\ y=-x+9 \end{gathered}\)We graph each of the equation using the x and y-intercepts.
First Equation(y=2x-3)
When x=0
\(\begin{gathered} y=2x-3 \\ y=2(0)-3 \\ y=-3 \\ \implies(0,-3) \end{gathered}\)When y=0
\(\begin{gathered} 0=2x-3 \\ 2x=3 \\ x=\frac{3}{2} \\ x=1.5 \\ \implies(1.5,0) \end{gathered}\)Next, join the points (0,-3) and (1.5,0) as shown below:
Second Equation(y=-x+9)
When x=0
\(\begin{gathered} y=-x+9 \\ y=-0+9 \\ y=9 \\ \implies(0,9) \end{gathered}\)When y=0
\(\begin{gathered} 0=-x+9 \\ x=9 \\ \implies(9,0) \end{gathered}\)Next, join the points (0,9) and (9,0) on the same graph as shown below:
The point where the two lines intersect is the solution to the system of equations.
Therefore, the solution is (4,5).


when we say that an estimated regression coefficient is statistically significant, we mean that it is statistically different from 1. true or false
Answers
The statement that "an estimated regression coefficient is statistically significant if it is statistically different from 1" is false.
When is the estimated regression coefficient statistically significant?When we say that an estimated regression coefficient is statistically significant, we mean that it is statistically different from zero, not from 1.
The reason for this is that the null hypothesis in a hypothesis test for a regression coefficient is typically that the true value of the coefficient is zero. Therefore, if we reject the null hypothesis and find that the estimated coefficient is statistically significant, we conclude that there is evidence to suggest that the coefficient is not equal to zero and therefore has a non-zero effect on the response variable.
In some cases, we may be interested in testing whether a regression coefficient is equal to a specific value, such as 1. However, this would be a different hypothesis test with a different null hypothesis, and the result of this test would not necessarily be related to whether the coefficient is statistically significant or not.
Therefore, the statement that "an estimated regression coefficient is statistically significant if it is statistically different from 1" is not accurate.
Learn more about estimated regression coefficient on:
https://brainly.com/question/17004137
#SPJ1
B) What is the cost of making 35 items?
And c. The domain

Answers
The cost of making 35 items is 1100 and the domain is (-∞,∞)
The cost of making 35 items :
x = 35plug the value into the cost equation
C(35) = 10(35) + 800
C(35) = 350 + 800
C(35) = 1100
Hence, cost of making 35 items is 1100
The domain of the functionSince the value of X can be any real number, we can plug in any real number for x and get a real number output.
Hence, the domain = (-∞,∞)
Learn more on domain: https://brainly.com/question/28934802
#SPJ1
Can anyone help me out with this please!

Answers
Answer:
\(h(x)=\frac{1}{4}|x|\)
Step-by-step explanation:
In order to vertically stretch a function, we just need to multiply the function by our stretch factor.
So, we have the function:
\(g(x)=|x|\)
We want to find the equation of this function vertically shrunk by a factor of 1/4. So, multiplied the function by 1/4:
\(h(x)=\frac{1}{4}|x|\)
And this will be our answer :)
Section 5.2 Problem 21:
Solve the initial value problem and graph the solution.
\(y'' + 4y' + 10y = 0\)
\(y(0) = 3\)
\(y'(0) = - 2\)
Answers
Answer:
\(y(x)=e^{-2x}[3cos(\sqrt{6}x)+\frac{2\sqrt{6}}{3}sin(\sqrt{6}x)]\) (See attached graph)
Step-by-step explanation:
To solve a second-order homogeneous differential equation, we need to substitute each term with the auxiliary equation \(am^2+bm+c=0\) where the values of \(m\) are the roots:
\(y''+4y'+10y=0\\\\m^2+4m+10=0\\\\m^2+4m+10-6=0-6\\\\m^2+4m+4=-6\\\\(m+2)^2=-6\\\\m+2=\pm\sqrt{6}i\\\\m=-2\pm\sqrt{6}i\)
Since the values of \(m\) are complex conjugate roots, then the general solution is \(y(x)=e^{\alpha x}[C_1cos(\beta x)+C_2sin(\beta x)]\) where \(m=\alpha\pm\beta i\).
Thus, the general solution for our given differential equation is \(y(x)=e^{-2x}[C_1cos(\sqrt{6}x)+C_2sin(\sqrt{6}x)]\).
To account for both initial conditions, take the derivative of \(y(x)\), thus, \(y'(x)=-2e^{-2x}[C_1cos(\sqrt{6}x+C_2sin(\sqrt{6}x)]+e^{-2x}[-C_1\sqrt{6}sin(\sqrt{6}x)+C_2\sqrt{6}cos(\sqrt{6}x)]\)
Now, we can create our system of equations given our initial conditions:
\(y(x)=e^{-2x}[C_1cos(\sqrt{6}x)+C_2sin(\sqrt{6}x)]\\\\y(0)=e^{-2(0)}[C_1cos(\sqrt{6}(0))+C_2sin(\sqrt{6}(0))]=3\\\\C_1=3\)
\(y'(x)=-2e^{-2x}[C_1cos(\sqrt{6}x+C_2sin(\sqrt{6}x)]+e^{-2x}[-C_1\sqrt{6}sin(\sqrt{6}x)+C_2\sqrt{6}cos(\sqrt{6}x)]\\\\y'(0)=-2e^{-2(0)}[C_1cos(\sqrt{6}(0))+C_2sin(\sqrt{6}(0))]+e^{-2(0)}[-C_1\sqrt{6}sin(\sqrt{6}(0))+C_2\sqrt{6}cos(\sqrt{6}(0))]=-2\\\\-2C_1+\sqrt{6}C_2=-2\)
We then solve the system of equations, which becomes easy since we already know that \(C_1=3\):
\(-2C_1+\sqrt{6}C_2=-2\\\\-2(3)+\sqrt{6}C_2=-2\\\\-6+\sqrt{6}C_2=-2\\\\\sqrt{6}C_2=4\\\\C_2=\frac{4}{\sqrt{6}}\\ \\C_2=\frac{4\sqrt{6}}{6}\\ \\C_2=\frac{2\sqrt{6}}{3}\)
Thus, our final solution is:
\(y(x)=e^{-2x}[C_1cos(\sqrt{6}x)+C_2sin(\sqrt{6}x)]\\\\y(x)=e^{-2x}[3cos(\sqrt{6}x)+\frac{2\sqrt{6}}{3}sin(\sqrt{6}x)]\)
![Section 5.2 Problem 21: Solve the initial value problem and graph the solution.[tex]y'' + 4y' + 10y =](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/Sb0iKGE5QbuW88WfWGLqhf4EwLpGLVID.png)
Arnie has a storage unit that measures 7 ft by 6 ft by 9 ft. He will pack in cylindrical canisters into the unit and needs to determine how many will fit within the space. Each cylinder has a height of 2 ft and radius of 1.6 ft.
How many canisters will fit in Arnie’s storage unit? Use 3.14 for
π and round to the nearest canister.
Answers
We need to round to the nearest canister, Arnie can fit approximately 23 canisters in his storage unit.
To determine the number of canisters that will fit in Arnie's storage unit, we need to calculate the available space and the space occupied by each canister.
The storage unit has dimensions of 7 ft by 6 ft by 9 ft,
resulting in a total volume of 7 x 6 x 9 = 378 cubic feet.
Each canister has a height of 2 ft and a radius of 1.6 ft,
which means it occupies a cylindrical volume of
π ×\((1.6^2)\)× 2 = 16.128 cubic feet.
To find the number of canisters that fit,
we divide the total volume of the storage unit by the volume of each canister:
378 / 16.128 = 23.409 canisters.
The actual number of canisters may vary depending on the arrangement and orientation within the storage unit. This calculation assumes that the canisters are placed in a regular grid pattern with no wasted space.
Learn more about dimensions here:
https://brainly.com/question/31106945
#SPJ1