The area of the figure is square units.
3 units, 8 units, 3 units, 9 units, 3 units, 21 units
Answers
The area of the figure is 114 square units.
To determine the area of the figure, we need to identify its shape.
From the given dimensions, it appears that we have three rectangular sections.
The first section has a length of 3 units and a width of 8 units, giving us an area of 3 \(\times\) 8 = 24 square units.
The second section has a length of 3 units and a width of 9 units, resulting in an area of 3 \(\times\) 9 = 27 square units
The third section has a length of 3 units and a width of 21 units, yielding an area of 3 \(\times\) 21 = 63 square units.
To find the total area of the figure, we need to sum up the areas of the individual sections:
Total area = 24 + 27 + 63 = 114 square units.
Therefore, the area of the figure is 114 square units.
It's important to note that without a clear description or diagram of the figure, it's challenging to provide an accurate interpretation.
The given dimensions could represent various arrangements, and the resulting area would vary accordingly.
For similar question on area.
https://brainly.com/question/25292087
#SPJ8
Related Questions
Hiii this due today can you draw a digram for 5 times 20 please THIS IS DUE TODAY THANK You
Answers
Answer:
draw the diagram and multiply 5x20
What is the value of the expression 6.5 - (-7.25)?
Answers
Answer:
13.75
Step-by-step explanation:
Slash and dash. turn the both minuses into positives and add like normal. 6.5 plus 7.25 equals 13.75.
if you have 3/4 cup of flour how many eighths do you have?
Answers
Answer:
You have and you want to know how many eighths you have
You need to have the denominator to eighths to find out correctly
So 4 times 2 equals 8 but what you do one side (denominator/bottom) has to be done on the other side (numerator/top) to make it the equal value of the original fraction
So ×≈
So that means that you have 6, eighths
Answer: You have 6 eights of flour
Step-by-step explanation:
Reduce the equation to one of the standard forms, classify the surface, and sketch it. (a) z^2 = 4x^2 + 9y^2 + 36 (b) x = 2y^2 + 3z^2 (c) 4x^2 + y^2 + 4z^2 - 4y - 24z + 36 = 0 (d) x^2 - y^2 + z^2 - 4x - 2y - 2z = 0
Answers
Reduced the equation to one of the standard forms
(a) z²/36 = 4x²/36 + 9y²/36 + 1
(b) x = 2y² + 3z
(c) (x + y + 2z)²
(d) (x - y + z)²
What do you mean by equation?It is represented by an equal sign (=) and is used to solve for unknown values or to describe relationships between variables. Equations can be simple or complex, involving basic arithmetic operations or advanced mathematical concepts like trigonometry and calculus.
An equation can be used to solve for a single unknown value, for example, the equation 2x + 3 = 7 can be solved for x by subtracting 3 from both sides, giving us 2x = 4 and then dividing both sides by 2, giving us x = 2. In this example, x = 2 is the solution to the equation.
(a) The equation z² = 4x² + 9y² + 36 can be reduced to the standard form of an ellipsoid by dividing both sides by 36:
z²/36 = 4x²/36 + 9y²/36 + 1
This is the equation of an ellipsoid with center at the origin and semi-axes of length 3, 3/2, and 6, respectively. The surface is a solid and is classified as an oblate ellipsoid.
(b) The equation x = 2y² + 3z² is a standard parabolic cylinder equation. The surface is a cylinder and is classified as a parabolic cylinder.
(c) The equation 4x² + y² + 4z² - 4y - 24z + 36 = 0 can be reduced to the standard form of an ellipsoid by dividing both sides by 36:
x² + y² + 4z² - 4y - 24z + 36 = 0
= (x + y + 2z)²
This is the equation of an ellipsoid with center at the origin and semi-axes of length 3, 3, and 6, respectively. The surface is a solid and is classified as an oblate ellipsoid.
(d) The equation x² - y² + z² - 4x - 2y - 2z = 0 can be reduced to the standard form of a hyperboloid of two sheets by subtracting 1 from both sides:
x² - y² + z² - 4x - 2y - 2z + 1 = 1
= (x - y + z)²
This is the equation of a hyperboloid of two sheets with center at the point (-2, -1, -1) and semi-axes of length √2, √2, and √6, respectively. The surface is a solid and is classified as a hyperboloid of two sheets.
To know more about hyperboloid visit:
brainly.com/question/28356129
#SPJ4
After reducing the equation to one of the standard forms, the equations will be (a) z²/36 = 4x²/36 + 9y²/36 + 1, (b) x = 2y² + 3z, (c) (x + y + 2z)², and (d) (x - y + z)²
What do you mean by equation?It is represented by an equal sign (=) and is used to solve for unknown values or to describe relationships between variables. Equations can be simple or complex, involving basic arithmetic operations or advanced mathematical concepts like trigonometry and calculus.
An equation can be used to solve for a single unknown value, for example, the equation 2x + 3 = 7 can be solved for x by subtracting 3 from both sides, giving us 2x = 4 and then dividing both sides by 2, giving us x = 2. In this example, x = 2 is the solution to the equation.
(a) The equation z² = 4x² + 9y² + 36 can be reduced to the standard form of an ellipsoid by dividing both sides by 36:
z²/36 = 4x²/36 + 9y²/36 + 1
This is the equation of an ellipsoid with center at the origin and semi-axes of length 3, 3/2, and 6, respectively. The surface is a solid and is classified as an oblate ellipsoid.
(b) The equation x = 2y² + 3z² is a standard parabolic cylinder equation. The surface is a cylinder and is classified as a parabolic cylinder.
(c) The equation 4x² + y² + 4z² - 4y - 24z + 36 = 0 can be reduced to the standard form of an ellipsoid by dividing both sides by 36:
x² + y² + 4z² - 4y - 24z + 36 = 0
= (x + y + 2z)²
This is the equation of an ellipsoid with center at the origin and semi-axes of length 3, 3, and 6, respectively. The surface is a solid and is classified as an oblate ellipsoid.
(d) The equation x² - y² + z² - 4x - 2y - 2z = 0 can be reduced to the standard form of a hyperboloid of two sheets by subtracting 1 from both sides:
x² - y² + z² - 4x - 2y - 2z + 1 = 1
= (x - y + z)²
This is the equation of a hyperboloid of two sheets with center at the point (-2, -1, -1) and semi-axes of length √2, √2, and √6, respectively. The surface is a solid and is classified as a hyperboloid of two sheets.
To know more about hyperboloid visit:
brainly.com/question/28356129
#SPJ4
PLSSS HELP I LITERALLY HAVE NO CLUE WHAT IM DOING

Answers
1st row
1. 2x + x + x, x = 0
Plug in 0 as x.
0 + 0 + 0 = 0
2. 2x + x + x, x = 1
Plug in 1 as x.
2 + 1 + 1 = 4
3. 2x + x + x, x = 2
Plug in 2 as x.
4 + 2 + 2 = 8
2nd row
1. 4x, x = 0
Plug in 0 as x.
4 * 0 = 0
2. 4x, x = 1
Plug in 1 as x.
4 * 1 = 4
3. 4x, x = 2
4 * 2 = 8
Notice how the answers are the same.
This is because 2x + x + x = 4x, meaning they are the same equation.
Answer:
Attached in file
Step-by-step explanation:
What does this mean by substitution?
The act of substituting in algebra / pre-algebra / etc is plugging in a number for 'x'
In this question, they are wanting you to plug in 0, 1, and 2 to two different equations (2x+x+x and 4x) to see if they are the same equations.
(I'm going to try and make a graph, as visual learning helps)
| 2x+x+x 4x
x=0| a b
x=1 | c d
x=2| e f
Now I know that this is not perfect, but I inputted letters so that you know what I am solving for.
Solve for a:
Plug in x=0
2(0) + 0 + 0
2*0 = 0
0 + 0 + 0 = 0
So, a = 0 (What I am saying is the first blank is a, the blank next to it is b, etc)
Solve for b:
Plug in x=0
4(0) = 0
So, b = 0
Solve for c:
Plug in x=1
2(1) + 1 + 1
2 + 1 + 1
= 2 + 2
=4
b = 4
Solve for d:
Plug in x=1
4(1) = 4
d=4
Solve for e:
Plug in x=2
2(2) + 2 + 2
4 + 2 + 2
4 + 4
=8
e=8
Solve for f:
Plug in x=2
4(2)
f=8
There we go! I annotated this picture to have these values plugged into their respective spots!!
Hope this helped!!

ALGEBRA please put a very small explanation to the awnser


Answers
Certainly! The problem can be solved using the Pythagorean theorem,
which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In this case, the ladder acts as the hypotenuse, and we need to find the length of the vertical side (height) it reaches up the wall.
The ladder forms the hypotenuse, and its length is given as 12 meters. The distance from the foot of the ladder to the base of the wall represents one side of the triangle, which is 4.5 meters.
By substituting the given values into the Pythagorean theorem equation: (12m)^2 = h^2 + (4.5m)^2, we can solve for the unknown height 'h'.
Squaring 12m gives us 144m^2, and squaring 4.5m yields 20.25m^2. By subtracting 20.25m^2 from both sides of the equation, we isolate 'h^2'.
We then take the square root of both sides to find 'h'. The square root of 123.75m^2 is approximately 11.12m.
Therefore, the ladder reaches a height of approximately 11.12 meters up the wall.
For more questions Pythagorean theorem:
https://brainly.com/question/343682
#SPJ8
1. The proportion, p, of consumers who shop with coupons
is the ratio of the number, C, of consumers who use coupons
to the number, N, of consumers asked. Write an equation
for the proportion of consumers who shop with coupons.
Answers
The equation for the proportion, p, of consumers who shop with coupons is: p = C/N where C is the number of consumers who use coupons and N is the total number of consumers asked.
What is equation?An equation is a mathematical statement that indicates the equality of two expressions. It consists of two expressions separated by an equal sign (=). The expression on the left side of the equal sign is equivalent to the expression on the right side. Equations can have one or more variables, which are usually represented by letters such as x, y, or z. The goal in solving an equation is to determine the value(s) of the variable(s) that make the equation true. This involves manipulating the expressions on both sides of the equal sign using algebraic operations such as addition, subtraction, multiplication, and division, to isolate the variable on one side of the equation. Equations are used in many areas of mathematics and science to represent relationships between variables and to solve problems. They are also used in various fields such as engineering, physics, and economics to model real-world situations and make predictions based on mathematical analysis.
Here,
This equation represents the ratio of the number of consumers who use coupons to the total number of consumers. It is commonly used in statistics and market research to measure the prevalence of a certain behavior or preference among a population. By calculating the proportion of consumers who use coupons, businesses can make informed decisions about their pricing strategies, promotions, and advertising campaigns.
To know more about equation,
https://brainly.com/question/2228446
#SPJ9
one unit of a is made of two units of b, three units of c, and two units of d. b is composed pf one unit of e and two units of f. c is made of two units of f and one unit of d. e is made of two units of d. items a, c, d, and f have one-week lead times; b and e have lead times of two weeks. lot-for-lot (l4l) lot sizing is used for items a, b, c, and d; lots of size 50 and 180 are used for items e and f, respectively. item c has on-hand (beginning) inventory of 15; d has an on-hand inventory of 50; all other items have zero beginning inventories. we are scheduled to receive 20 units of item e in week 2; there ae no other scheduled receipts. construct simple and low-level-coded bill-to-materials (product structure tree) and indented and summarized parts lists. if 20 units of a are required in week 8, use the low-level-coded bill-of-materials to find the necessary planned-order releases for all components.
Answers
Data handling is the process of ensuring that research data is stored, archived, or disposed of in a safe and secure manner during and after the conclusion of a research project.
The following are the given details:
Item Leadtime On hand Inventory Lot sizing criteria Schedulereceipts
A 2 0 L4L 10 in week 2
B 1 0 LAL 0
C 1 10 50 0
D 2 0 50 0
E 1 50 180 50 in week 1
F 1 180 L4L 50 in week 1
The Complete MRP schedule can be seen in the attached images below:
To know more about data handling:
https://brainly.com/question/15877351
#SPJ4
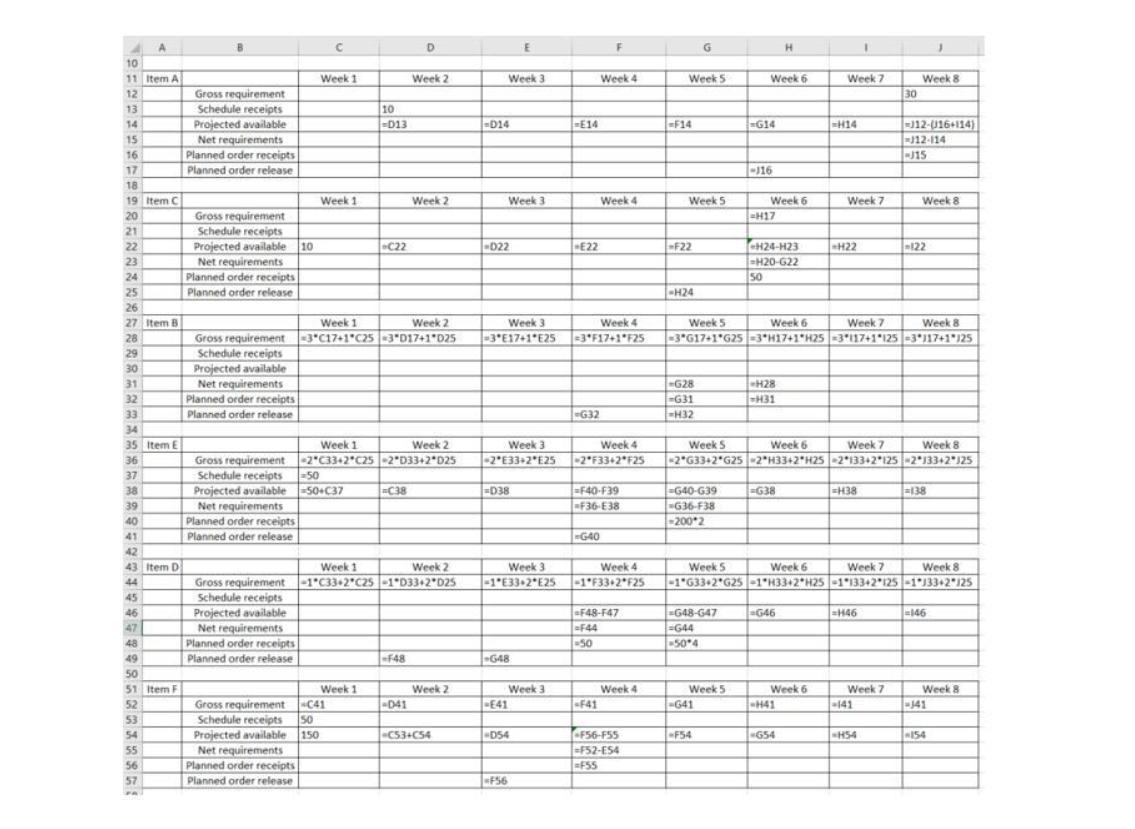

The gross requirements for each component are as follows:
b = 2 x a = 44 units in week 7
c = 3 x a = 66 units in week 7
d = 2 x e + 1 x c + 2 x a
= 110 units in week 3, 56 units in week 6, 44 units in week 7
e = 1 x b = 44 units in week 5
f = 2 x b + 2 x c = 88 units in week 5 and 112 units in week 6
Net requirements = Gross requirements - Projected on hand
Projected on hand = Planned order receipts - net requirements
Planned order receipts = net requirements
Planned order releases = net requirements adjusted as per the lead time
To read more about the Gross requirements:
https://brainly.com/question/29431904
#SPJ4



After begging his parents for 3 years, Ed is finally going to clown college! On the first day, his juggling instructor divides a box of bean bags equally among the 17 clowns in Ed's class. Each clown gets 4 bean bags. Which equation can you use to find the number of bean bags b in the instructor's box? Solve this equation for b to find the number of bean bags in the instructor's box. bean bags Questions
Answers
The equation that can be used to determine the number of bean bags in the instuctor's box is b = 17 x 4.
The number of bean bags in the instructor's box is 68.
What is multiplication?
Multplication is a mathematcial operation that can be used to determine the product of two or more numbers. The sign used to represent multiplication is ×.
To learn more about multiplication, please check: https://brainly.com/question/13814687
4x + y = 0
y-intercept
Submit
Answers
In the figure, m∠4=74°
and m∠3=43°
. Find m∠1
and m∠2
.

Answers
Answer:
Based on the information given, we know that angles 3 and 4 are supplementary (they add up to 180 degrees) and angles 2 and 4 are vertical angles (they are congruent). Therefore, we can write:
m∠4 + m∠3 = 180 (since angles 3 and 4 are supplementary)
m∠4 = m∠2 (since angles 2 and 4 are vertical angles)
Substituting m∠4 = m∠2 into the first equation, we get:
m∠2 + m∠3 = 180
Now we can solve for m∠2 and m∠3:
m∠3 = 43 (given)
m∠2 = 180 - m∠3 = 180 - 43 = 137
Since angles 1 and 2 are also supplementary, we can find m∠1 by subtracting m∠2 from 180:
m∠1 = 180 - m∠2 = 180 - 137 = 43
Therefore, m∠1 = 43 degrees and m∠2 = 137 degrees.
solve (2x - 3) (x + 2) = 0
Answers
Answer:
x=3/2
x=-2
Step-by-step explanation:
A) Find an equation for the line perpendicular to the tangent line to the curve y=x^3-4x+6 at the point (2,6)
-The equation is y=
b) What is the smallest slope on the curve? At what point on the curve does the curve have this slope?
-The smallest slope on the curve is
-The curve has the smallest slope at the point
c) Find equations for the tangent lines to the curve at the points where the slope of the curve is 8.
Answers
Answer:
f(x) = x³ - 4x + 6
f'(x) = 3x² - 4
a) f'(2) = 3(2²) - 4 = 12 - 4 = 8
6 = 8(2) + b
6 = 16 + b
b = -10
y = 8x - 10
b) 3x² - 4 = 0
3x² = 4, so x = ±2/√3 = ±(2/3)√3
= ±1.1547
f(-(2/3)√3) = 9.0792
f((2/3)√3) = 2.9208
c) 3x² - 4 = 8
3x² = 12
x² = 4, so x = ±2
f(-2) = (-2)³ - 4(-2) + 6 = -8 + 8 + 6 = 6
6 = -2(8) + b
6 = -16 + b
b = 22
y = 8x + 22
f(2) = 6
y = 8x - 10
The equation perpendicular to the tangent is y = -1/8x + 25/4
-The smallest slope on the curve is 2.92
The curve has the smallest slope at the point (1.15, 2.92)
The equations at tangent points are y = 8x + 16 and y = 8x - 16
Finding the equation perpendicular to the tangentFrom the question, we have the following parameters that can be used in our computation:
y = x³ - 4x + 6
Differentiate
So, we have
f'(x) = 3x² - 4
The point is (2, 6)
So, we have
f'(2) = 3(2)² - 4
f'(2) = 8
The slope of the perpendicular line is
Slope = -1/8
So, we have
y = -1/8(x - 2) + 6
y = -1/8x + 25/4
The smallest slope on the curveWe have
f'(x) = 3x² - 4
Set to 0
3x² - 4 = 0
Solve for x
x = √[4/3]
x = 1.15
So, we have
Smallest slope = (√[4/3])³ - 4(√[4/3]) + 6
Smallest slope = 2.92
So, the smallest slope is 2.92 at (1.15, 2.92)
The equation of the tangent lineHere, we set f'(x) to 8
3x² - 4 = 8
Solve for x
x = ±2
Calculate y at x = ±2
y = (-2)³ - 4(-2) + 6 = 6: (-2, 0)
y = (2)³ - 4(2) + 6 = 6: (2, 0)
The equations at these points are
y = 8x + 16
y = 8x - 16
Read more about tangent lines at
https://brainly.com/question/21595470
#SPJ1
Michael saw a pair of jeans that he really wants to buy. The price of the jeans is $25.60. He saw that they go on sale for weekend and will be 15% off. How much will he save?
Answers
Answer:
$21.76
Step-by-step explanation:
15% of $25.60= $3.84
$25.60-$3.84= $21.76
the sum of two numbers is 45 and the different is 21.what are the numbers
Answers
a - b = 21
a = 21 + b
Use substitution
21 + b + b = 45
2b = 24
b = 12
45 - 12 = 33
The numbers are 33 and 12
What is f(g(13))?
A mapping diagram is shown.

Answers
Answer:
(c) 32
Step-by-step explanation:
Given a map between x, g(x), and f(g(x)), you want to find f(g(13)).
Using a mapYou want the function value that results when 13 is the argument of g(x), and g(x) is the argument of f(x).
Locate the input (13) in the left column of the diagram. Follow the arrow to find g(13) = 16. Follow the arrow again to find f(16) = 32.
f(g(13)) = 32
Pat made a total of 48 pottery plates and cups, how many plates did she make?
Answers
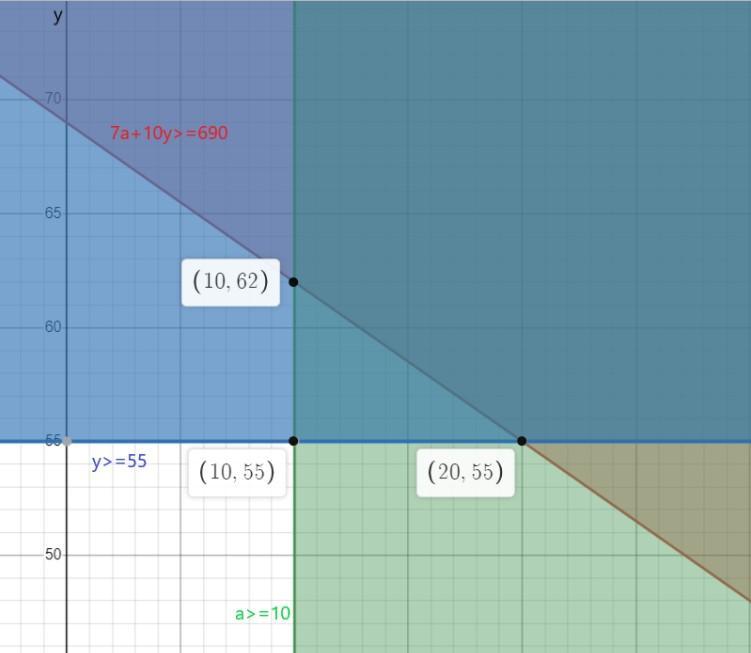
The drama club is selling tickets to their play to raise money for the show's expenses.
Each student ticket sells for $7 and each adult ticket sells for $10. The auditorium can
hold no more than 85 people. The drama club must make no less than $690 from
ticket sales to cover the show's costs. Also, they must sell a minimum of 10 student
tickets and at least 55 adult tickets. If a represents the number of student tickets sold
and y represents the number of adult tickets sold, write and solve a system of
inequalities graphically and determine one possible solution.

Answers
On solving the inequalities a ≥ 10, y ≥ 55, 7a + 10y ≥ 690, the solution is obtained as (20,55).
What is an inequality?
In Algebra, an inequality is a mathematical statement that uses the inequality symbol to illustrate the relationship between two expressions. An inequality symbol has non-equal expressions on both sides. It indicates that the phrase on the left should be bigger or smaller than the expression on the right, or vice versa.
Use the variables a and y to represent the number of student and adult tickets sold, respectively.
Then write the following system of inequalities -
a ≥ 10 (they must sell a minimum of 10 student tickets)
y ≥ 55 (they must sell at least 55 adult tickets)
7a + 10y ≥ 690 (they must make no less than $690 from ticket sales)
The first two inequalities are constraints on the number of tickets sold, and the third inequality represents the revenue constraint.
To find a possible solution, graph these inequalities on a coordinate plane and look for the feasible region that satisfies all three inequalities.
Alternatively, solve the system of inequalities using algebra.
First, simplify the third inequality by subtracting 7a from both sides -
10y ≥ 690 - 7a
Then, divide both sides by 10 -
y ≥ (690 - 7a)/10
This inequality represents the revenue constraint in terms of the number of student tickets sold.
Now combine the revenue constraint with the other two constraints -
a ≥ 10
y ≥ 55
y ≥ (690 - 7a)/10
Use substitution to solve for a in terms of y -
y ≥ (690 - 7a)/10
10y ≥ 690 - 7a
7a ≥ 690 - 10y
a ≥ (690 - 10y)/7
To find a possible solution, substitute a = (690 - 10y)/7 into the other two constraints -
(690 - 10y)/7 ≥ 10
y ≥ 55
These inequalities can be simplified -
690 - 10y ≥ 70
y ≥ 55
The first inequality can be solved for y -
-10y ≥ -620
y ≤ 62
Since it is known y ≥ 55, the feasible values for y are between 55 and 62, inclusive -
55 ≤ y ≤ 62
Now use the expression for a in terms of y to find the corresponding values of a -
a = (690 - 10y)/7
For each value of y between 55 and 62, inclusive, we can calculate a and check whether it satisfies the constraints -
a ≥ 10
y ≥ 55
7a + 10y ≥ 690
For example, when y = 55 -
a = (690 - 10(55))/7 = 20
7a + 10y = 7(20) + 10(55) = 690
Therefore, these values satisfy all three constraints, so one possible solution is a = 20 and y = 55.
To learn more about inequality from the given link
https://brainly.com/question/11234618
#SPJ1
"Match the expression and its value to the value of x that gives the expression its value by filling in the box in the correct column.
Evaluate the expression 4 n-5 r for n=-2 and r=3
(A) 23
(C) 7
(B) -7
(D) -23
The surface area for a rectangular prism with a square base is given the expression 2 s²+4 s h, where s is the side length of the square h is the height of the prism. What is the surface area in square feet rectangular prism when s=4 feet and h=6feet?"

Answers
Value of the expression 4n - 5r when n = -2 and r = 3 is -23.
The surface area in square feet rectangular prism when s=4 feet and h=6feet is 128 square feet.
What do you mean by algebraic expression?
The concept of algebraic expressions is the use of letters or alphabets to represent numbers without providing their precise values. We learned how to express an unknown value using letters like x, y, and z in the fundamentals of algebra. Here, we refer to these letters as variables. Variables and constants can both be used in an algebraic expression. A coefficient is any value that is added before a variable and then multiplied by it.
Given expression:
4n - 5r
When n = -2 and r = 3
The value of the expression become,
4(-2) - 5(3)
= -8 - 15
= -23
Hence, option D is correct.
Now, it is given that the surface area for a rectangular prism with a square base is given by the expression 2s²+4sh, where s is the side length of the square h is the height of the prism.
The surface area in square feet rectangular prism when s=4 feet and h=6feet is
2\((4)^{2}\) + 4(4)(6)
= 2(16) + 96
= 32 + 96
= 128 square feet
therefore, the surface area in square feet rectangular prism when s=4 feet and h=6feet is 128 square feet.
To learn more about the algebraic expression from the given link.
https://brainly.com/question/4344214
#SPJ4
2.1.2 Linear Tables and Graphs (Algebra 1)
The question is on the image below


Answers
Answer:
Step-by-step explanation:
1). Let the equation of a line is,
y = mx + b
Here, m = slope of the line
b = y-intercept
From the graph attached,
Slope = \(\frac{\text{Rise}}{\text{Run}}\) = \(\frac{1}{4}\)
y-intercept = -2
Equation → y = \(\frac{1}{4}x-2\)
2). Slope of the line = \(\frac{\text{Rise}}{\text{Run}}=\frac{3}{4}\)
y-intercept 'b' = -3
Equation → y = \(\frac{3}{4}x-4\)
3). Slope of the line = \(\frac{\text{Rise}}{\text{Run}}=\frac{-5}{0.75}\)
= \(-\frac{20}{3}\)
y-intercept = 5
Equation → y = \(-\frac{20}{3}+5\)
4). Slope of the line = \(\frac{\text{Rise}}{\text{Run}}=\frac{-2}{4}=-\frac{1}{2}\)
y-intercept = 4
Equation → y = \(-\frac{1}{2}x+4\)
5). Since, line is passing through origin (0, 0)
y-intercept = 0
Slope = \(\frac{\text{Rise}}{\text{Run}}=\frac{1}{1}\)
Equation → y = x
6). Slope of the line = \(\frac{\text{Rise}}{\text{Run}}=\frac{1}{4}\)
y-intercept = -4
Equation → y = \(\frac{1}{4}x-4\)
need help thankssssss

Answers
Answer:
301.44
Step-by-step explanation:
V=π r² h
V=π (4)² (12)
V= 603.19
divide by 2 to find half full: ≈ 301
301.44
Below is the graph of . Translate it to make it the graph of . y2468-2-4-6-8x2468-2-4-6-8
Answers
The graph of y = x^2 should be translated by 1 unit to the right and 3 units up.
What is a translation?In Mathematics, the translation of a geometric figure to the right simply means adding a digit to the value on the x-coordinate (x-axis) of the pre-image of a function while a geometric figure that is translated upward simply means adding a digit to the value on the y-coordinate (y-axis) of the pre-image.
In Mathematics, a vertical translation to the positive y-direction (upward) is modeled by this mathematical expression g(x) = f(x) + N.
Where:
N represents an integer.g(x) and f(x) represent a function.Therefore, we have the following:
f(x) = x^2
g(x) = f(x - 1) + N
g(x) = (x - 1)^2 + 3
Read more on translation here: brainly.com/question/16486008
#SPJ1


In a class of pupils, 13 play the flute and
piano.
12 play the flute only.
3 play the piano only.
7 play neither instrument.
How many pupils are in the class?
Answers
Answer:
35 Pupils
Step-by-step explanation:
You would add up each number: 13 + 12 + 3 + 7 = 35. I Hope This Helps :)
Answer:
45
Step-by-step explanation:
13 + 12 + 3 + 7
slope of line passes through (7/20, 8/3) and (3/8, 7/9)
Answers
Answer:
\(slope = \dfrac{-680}{9}\)
Step-by-step explanation:
We are given coordinates of two points:
Let the points be A and B respectively:
\(A(\dfrac{7}{20}, \dfrac{8}{3})\\B(\dfrac{3}{8}, \dfrac{7}{9})\)
To find the slope of line AB.
Formula for slope of a line passing through two points with coordinates \((x_1, y_1)\) and \((x_2,y_2)\) is given as:
\(m = \dfrac{y_2- y_1}{x_2- x_1}\)
Here, we have:
\(x_2 = \dfrac{3}{8}\\x_1 = \dfrac{7}{20}\\y_2 = \dfrac{7}{9}\\y_1 = \dfrac{8}{3}\\\)
Putting the values in formula:
\(m = \dfrac{\dfrac{7}{9}- \dfrac{8}{3}}{\dfrac{3}{8}- \dfrac{7}{20}}\\\Rightarrow m = \dfrac{\dfrac{7-24}{9}}{\dfrac{15-14}{40}}\\\Rightarrow m = \dfrac{\dfrac{-17}{9}}{\dfrac{1}{40}}\\\Rightarrow m = \dfrac{-17\times 40}{9}\\\Rightarrow m = \dfrac{-680}{9}\)
So, the slope of line AB passing through the given coordinates is:
\(m = \dfrac{-680}{9}\)
Music students and art students at a middle school were surveyed to choose a cardiovascular activity: playing sports or dancing.
Do you prefer dancing or playing sports?
Playing sports Dancing Row totals
Music students 32 15 47
Art students 31 22 53
Column totals 63 37 100
What is the marginal frequency of students who chose dancing?
15
22
37
53
Answers
The marginal frequency of students who chose dancing is 37.
The correct answer to the given question is option 3.
The marginal frequency of students who chose dancing can be calculated by adding up the number of students who chose dancing in each row or column. In this case, we need to add up the number of art students who chose dancing (22) and the number of music students who chose dancing (15), which gives us a total of 37. This is the marginal frequency of students who chose dancing.
Based on the survey results, it appears that a slightly higher percentage of art students prefer dancing (41.5%) compared to music students (31.9%). However, both groups of students seem to be fairly evenly split between dancing and playing sports, with a slight preference for playing sports overall.
It's worth noting that cardiovascular activity is important for overall health and well-being, and both dancing and playing sports can provide great opportunities for exercise and physical activity. Additionally, both activities can also be enjoyable and provide a sense of community and social connection, which is important for middle school students who are still developing their social skills and relationships. Ultimately, the choice between dancing and playing sports will depend on individual interests, preferences, and abilities.
For more such questions on frequency, click on:
https://brainly.com/question/254161
#SPJ8
Whose data did Kepler use to construct the laws of planetary motion? Aristarchus’s Aristotle’s Brahe’s Copernicus’s
Answers
Answer:
c or Brahe
Step-by-step explanation:
Answer: Option #4 or D. Copernicus’s
Step-by-step explanation: Correct answer is C on Edge.
This is a very tricky answer when you think about it!!
Because Kepler modified Copernicus's Model using data from Tycho Brahe.
Johannes Kepler accurately described the motions of the planets.
Used data collected by Tycho BraheConstructed the laws of planetary motion
Demonstrated that orbits were elliptical
Determined that planets move faster when closer to the Sun
Your bucket of Halloween candy has 125 pieces of candy in it. You decide that to ration yourself, you're going to only eat 5 pieces per day.
Answers
Answer:
you can eat candy for 25 days
Step-by-step explanation:
A ball is thrown up in the air from the top of a building. The function h(t) = -5t²+10t + 80 models the height of the ball, in feet, after t seconds. Graph this function.
What is the maximum height reached by the ball?
Answers
Answer:
Step-by-step explanation:
h(t)=-5t²+10t+80=-5(t²-2t+1-1)+80
=-5(t²+2t+1)+5+80
=-5(t-1)²+85
maximum height reached=85 ft


you have 10 bags full of coins. in each bag are infinite coins. but one bag is full of forgeries, and you can't remember which bag. but you do know that genuine coins weigh 1 gram, but forgeries weight 1.1 grams. you have to identify the bag with the forgeries in minimum readings. you are provided with a digital weighing machine.
Answers
If there are no forgeries, then total weight will be
= (1+2+3+4+5+6+7+8+9+10) = 55 grams
given that
they have 10 bags full of coins
in each bag are infinite coins.
but one bag is full of forgeries, and you can't remember which bag.
you know that genuine coins weigh= 1 gram
forgeries weight = 1.1 gram
now, we need to find which bag has forgeries in minimum readings
then take 1 coin from the first bag, 2 coins from the second bag . . . 10 coins from the tenth bag
If there are no forgeries, then total weight will be
= (1+2+3+4+5+6+7+8+9+10) = 55 grams
Therefore total weight should be 55 grams if the total weight is more than 55 grams then it has forgeries coins
To know more about weight:
https://brainly.com/question/23312072
#SPJ4
Total weight=55gm ,then there is no forgeries coin bag
1 bag with forgeries = take 1 coin from first bag
from 2 bag = take 2 coin
and similarly with all 10 bags.....
from 10th bag = take 10 coin
if there is no forgeries ,then total weight = (1+2+3+4+5+6+7+8+9+10)
=55gm
If bag weight 55.3 than we know that there are 3 forgeries.
So total weight=55 ,then there is no forgeries coin bag if weight is more than 55 than there is forgeries coin.
Learn more about coin here:-
https://brainly.com/question/29869268
#SPJ4
Factor the expression 2z²-17x+8
Answers
2(z²+4) -17x
1) Factorizing this polynomial 2z²-17x +8
2z²-17x +8 Let's find the LCM of 2, 8
2(z²+4) -17x
There's no step further to go since 17x and 2 can't be decomposed into prime factors.
2) So, the answer is
2(z²+4) -17x