the area of a parallelogram is 72 inches. what is the height?
Answers
9x8=72
the height should be 8?
Related Questions
Fill in the table 'using this function rule.
y = -5x+2
x
-1
0
1
2
y
0
0
0
X
4
S

Answers
Answer:
7, 2, -3, -8
Step-by-step explanation:
y = -5x + 2 Substitute in -1 for x
y = -5(-1) + 2
y = 5 + 2
y = 7
y = -5x + 2 Substitute in 0 for x
y = -5(0) + 2
y = 0 + 2
y = 2
y = -5 + 2 substitutes in 1 for x
y = -5(1) + 2
y = -5 + 2
y = -3
y = -5x + 2 Substitute in 2 for x
y = -5(2) + 2
y = -10 + 2
y = -8
Helping in the name of Jesus.
Find the exact length of the third side. (Pythagorean Theorem)

Answers
Answer:
3 sqrt(5) =c
Step-by-step explanation:
We can use the pythagorean theorem
a^2 + b^2 = c^2
3^2 + 6^2 = c^2
9+36 = c^2
45 = c^2
Take the square root of each side
sqrt(45) = sqrt(c^2)
sqrt(9)sqrt(5) = c
3 sqrt(5) =c
An English teacher reviewed 2 3 of an essay in 1 4 of an hour. At this rate, how many essays can she review in 1 hour? Simplify your answer and write it as a proper fraction, mixed number, or whole number. essays
Answers
The essays that she can review in 1 hour would be; 2 2/3.
What is a fraction?A fraction represents a part of a number or any number of equal parts.
We are given that English teacher reviewed 2 /3 of an essay in 1/ 4 of an hour.
Thus, Fraction of the essay reviewed = 2/3
Amount of time used = 1/4
Therefore, the fraction of essay for an hour can be calculated as;
= Fraction of the essay reviewed / Amount of time used
= 2/3 ÷ 1/4
= 2/3 × 4
= 8/3
= 2 2/3
Hence, She will review 2 2/3 essay.
Learn more about fractions on:
brainly.com/question/17220365
#SPJ1
Stephanie,Lois, and Tonya were all finding the value of the expression 4• (2)3. The final answers for each student are shown. Stephanie:4• (2)3 = 24 Lois: 4• (2)3 = 512 Tonya: 4• (2)3 = 32 who do you agree with? Why? The
Answers
Answer:
Stephanie
Step-by-step explanation:
Answer:
steaphanie im pretty sure
Step-by-step explanation:
The equation that represents ⨀A is (x+1)2+(y−1)2=16. Determine whether point B(3,1) is on the circle.
Answers
Answer:
Step-by-step explanation:
center=(-1,1)
radius=√16=4
distance between (-1,1) and (3,1)=√[(3+1)²+(1-1)²]=√[16+0]=√16=4=radius
Hence point lies on the circle.
473)1 12206115184 4•2D) -5 units(5.3)(5,-2)In the graph above, what's the distance between (5,-2) and (5, 3)?OA) 5 unitsOB) 1 unitOC) 3 units
Answers
Given:
The given two points are
\(\begin{gathered} (x1,y1)=(5,-2) \\ (x2,y2)=(5,3) \end{gathered}\)Required:
To find the distance between the given two points.
Explanation:
The diatnce between the two points is given by
\(\begin{gathered} d=\sqrt{(x2-x1)^2+(y2-y1)^2} \\ \\ =\sqrt{(5-5)^2+(3-(-2))^2} \\ \\ =\sqrt{0+5^2} \\ \\ =\sqrt{25} \\ \\ =5 \end{gathered}\)Final Answer:
The option A is correct.
5 units.
Liam will spin the pointer one time. What is the probability that the pointer will land on red?
Answers
Answer:
Step-by-step explanation:
What are the other colors?
if there are two colors ( red and another color ) then the probability of the pointer landing on red will be 1/2
similarly if there are 3 colors ( red and two other colors) then the probability of the pointer landing on red will be 1/3 ....
depends on how many colors are there
Jolene invests her savings in two bank accounts, one paying 3 percent and the other paying 9 percent simple
interest per year. She puts twice as much in the lower-yielding account because it is less risky. Her annual
interest is 3120 dollars. How much did she invest at each rate?
Amount invested at 3 percent interest is $____
Amount invested at 9 percent interest is $___
Answers
Let's denote the amount Jolene invested at 3 percent interest as 'x' dollars. Since she put twice as much in the lower-yielding account, the amount she invested at 9 percent interest would be '2x' dollars.
To calculate the interest earned from each account, we'll use the formula: Interest = Principal × Rate × Time.
For the 3 percent interest account:
Interest_3_percent = x × 0.03
For the 9 percent interest account:
Interest_9_percent = 2x × 0.09
We know that the total annual interest is $3120, so we can set up the equation:
Interest_3_percent + Interest_9_percent = 3120
Substituting the above equations, we have:
x × 0.03 + 2x × 0.09 = 3120
Simplifying the equation:
0.03x + 0.18x = 3120
0.21x = 3120
Dividing both sides of the equation by 0.21:
x = 3120 / 0.21
x = 14857.14
Therefore, Jolene invested approximately $14,857.14 at 3 percent interest and twice that amount, $29,714.29, at 9 percent interest.
Answer:
Step-by-step explanation:
X is the amount invested at 6%
Y is the amount invested at 9%
0.06X + 0.09Y = 4998
X = 2Y
0.06(2Y) + 0.09Y = 4998
.12Y + 0.09Y = 4998
0.21Y = 4998
21Y = 499800
Y = 499800/21 = 23800
So X = 2*23800 = 47600
$47,600 is invested at 6% and $23800 is invested at 9%
What is -5+8=-3y+10 equal I’m so lost
Answers
Answer:
y=7/3
Step-by-step explanation:
Answer:
7/3 = y
Step-by-step explanation:
-5+8=-3y+10
3 = -3y + 10
Subtract 10 from each side
3- 10 = -3y +10-10
-7 = -3y
Divide each side by -3
-7/-3 = -3y/-3
7/3 = y
Does anyone know how to directly ask a tutor a question? It’s like the option to is gone. Answer asap please!
Answers
Answer:
Just find the button to ask a question. Search around for it.
Step-by-step explanation:
Answer find the button to ask a question. you can search around for it
Step-by-step explanation:
Which of the following is a correct name for this angle? A. ABC B. ACB C. 2 CAB D. BAC
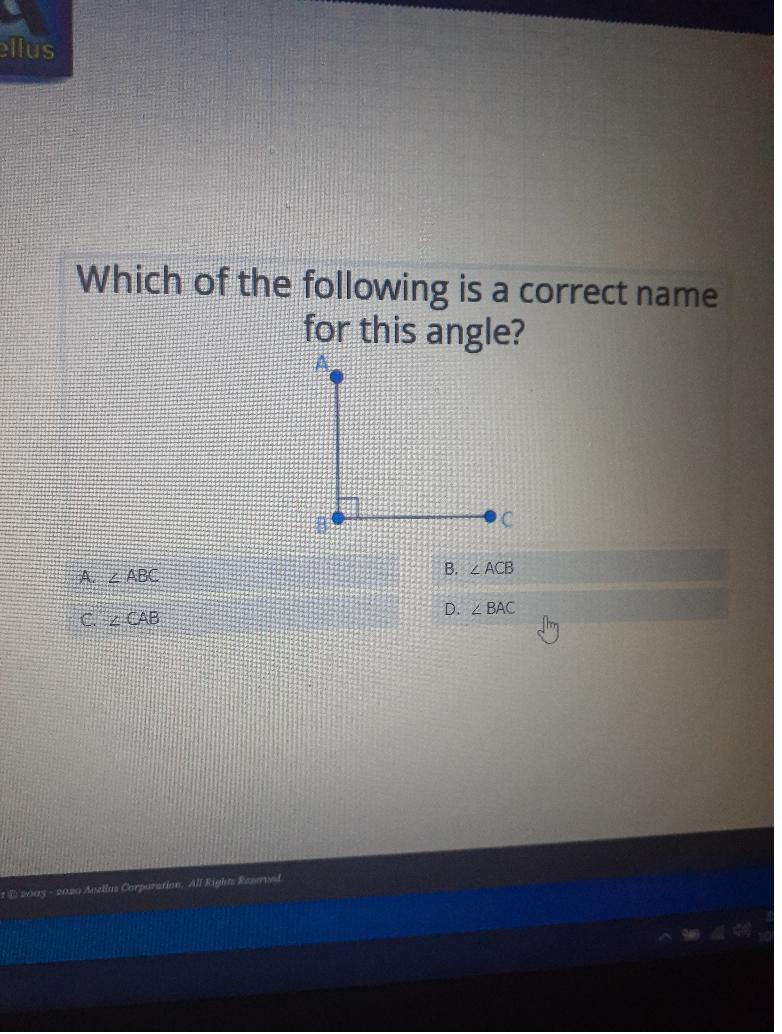
Answers
From the options given the correct answer is ∠ABC. This angle can also be called ∠CBA
State where in the ty-plane the hypotheses of the Existence and Uniqueness Theorem are satisfied for the equation y'=(ycot(2t))/(t^2+y^2+1)
Answers
We can conclude that the hypotheses of the Existence and Uniqueness Theorem are satisfied in any rectangular region in the ty-plane that does not contain the curve t² + y² = -1.
Where in the ty-plane the hypotheses of the existence and uniqueness theorem are satisfiedThe Existence and Uniqueness Theorem for first-order ordinary differential equations states that if a differential equation of the form y' = f(t, y) satisfies the following conditions in some rectangular region in the ty-plane:
1. f(t, y) is continuous in the region.
2. f(t, y) satisfies a Lipschitz condition in y in the region, i.e., there exists a constant L > 0 such that |f(t, y₁) - f(t, y₂)| ≤ L|y₁ - y₂| for all t and y₁, y₂ in the region.
then there exists a unique solution to the differential equation that passes through any point in the region.
In the case of the differential equation y' = (y cot(2t)) / (t² + y² + 1), we have:
f(t, y) = (y cot(2t)) / (t² + y² + 1)
This function is continuous everywhere except at the points where t² + y² + 1 = 0, which is the curve t² + y² = -1 in the ty-plane. Since this curve is not included in any rectangular region, we can say that f(t, y) is continuous in any rectangular region in the ty-plane.
To check if f(t, y) satisfies a Lipschitz condition in y, we can take the partial derivative of f with respect to y and check if it is bounded in any rectangular region. We have:
∂f/∂y = cot(2t) / (t² + y² + 1) - (2y² cot(2t)) / (t² + y² + 1)²
Taking the absolute value and simplifying, we get:
|∂f/∂y| = |cot(2t) / (t² + y² + 1) - (2y² cot(2t)) / (t² + y² + 1)²|
= |cot(2t) / (t² + y² + 1)| * |1 - (2y² / (t² + y² + 1)))|
Since 0 ≤ (2y² / (t² + y² + 1)) ≤ 1 for all t and y, we have:
1/2 ≤ |1 - (2y² / (t² + y² + 1)))| ≤ 1
Also, cot(2t) is bounded in any rectangular region that does not contain the points where cot(2t) is undefined (i.e., where t = (k + 1/2)π for some integer k). Therefore, we can find a constant L > 0 such that |∂f/∂y| ≤ L for all t and y in any rectangular region that does not contain the curve t² + y² = -1.
Learn more on differential equation here;
https://brainly.com/question/1164377
#SPJ1
What is the domain of the relation?

Answers
Decide whether the Experiment is a Binomial Experiment. If it is not, explain why:
You observe the gender of the next 850 babies born at a local hospital. The random variable represents the number of boys.
You draw a marble 350 times from a bag with three colors of marbles. The random variable represents the color of marble that is drawn.
Testing a cough suppressant using 820 people to determine if it is effective. The random variable represents the number of people who find the cough suppressant to be effective.
Answers
Answer:
Experiment 1 and 3 are clear binomial experiments.
Experiment 2 needs tweaking to be a binomial experiment.
Check Explanation.
Step-by-step explanation:
A binomial experiment is one in which
1) The probability of success doesn't change with every run or number of trials.
2) It usually consists of a fixed number of runs/trials with only two possible outcomes, a success or a failure.
3) The outcome of each trial/run of a binomial experiment is independent of one another.
Checking each of the experiments one at a time
- You observe the gender of the next 850 babies born at a local hospital. The random variable represents the number of boys.
For this experiment,
1) The probability of success doesn't change with every run or number of trials as it is a 50% chance that each child examined is a boy.
2) It consists of a fixed number of runs (850) with only two possible outcomes, success (if it's a boy) and failure (if it's a girl).
3) The probability of each trial being a boy is independent from all the other trials.
Hence, this experiment is a binomial experiment.
- You draw a marble 350 times from a bag with three colors of marbles. The random variable represents the color of marble that is drawn.
For this experiment,
1) If the marbles aren't being replaced after each draw, the probability of success, that is, picking a particular marble colour changes from trial to trial.
2) Although, it consist of a fixed number of runs/trials, there are more than two possible outcomes with 3 types of colours. Unless the experiment focuses on one colour and treats the other two colours as 'others', this condition too isn't satisfied.
3) Without replacement, the probability of success (picking a particular marble colour) in one trial isn't independent of the other trials.
This is not a binomial experiment as it doesn't satisfy all the required conditions to be one.
- Testing a cough suppressant using 820 people to determine if it is effective. The random variable represents the number of people who find the cough suppressant to be effective.
1) The probability of success doesn't change with every run or number of trials as it is the same chance that each person finds the cough suppressant to be effective.
2) It consists of a fixed number of runs (820) with only two possible outcomes, success (cough suppressant is effective) and failure (cough suppressant isn't effective).
3) The probability of each trial being a person that finds the cough suppressant to be effective, is independent from all the other trials.
Hence, this experiment is a binomial experiment.
Hope this Helps!!!
What is 6721 x 381 divided by 14 + 84
Answers
Let's break down the expression step by step:
1. Multiply: 6721 x 381 = 2,561,901.
2. Divide: 2,561,901 divided by 14 = 182,993.64 (rounded to two decimal places).
3. Add: 182,993.64 + 84 = 183,077.64 (rounded to two decimal places).
Therefore, the result of the expression 6721 x 381 divided by 14 + 84 is approximately 183,077.64.
Answer: 26129.6
Step-by-step explanation:
6721 x 381 = 2560701
14 + 84 = 98
2560701 / 98 = 26129.6
find x and y if the line through(0,0) and (x, y) has slope 1/2 and the line through (x, y) and (7,5) has slope 2
Answers
The values of the coordinates x and y is P ( 6 , 3 )
What is an Equation of a line?The equation of a line is expressed as y = mx + b where m is the slope and b is the y-intercept
And y - y₁ = m ( x - x₁ )
y = y-coordinate of second point
y₁ = y-coordinate of point one
m = slope
x = x-coordinate of second point
x₁ = x-coordinate of point one
The slope m = ( y₂ - y₁ ) / ( x₂ - x₁ )
Given data ,
Let the equation of line be represented as A
Now , the value of A is
Let the first point be P ( x , y )
Let the second point be Q ( 0 , 0 )
Now , the slope of the line is m₁ = ( y₂ - y₁ ) / ( x₂ - x₁ )
Substituting the values in the equation , we get
Slope m₁ = y / x
m₁ = 1/2
So , y/x = 1/2
And , x = 2y
Now , the third point is R ( 7 , 5 )
m₂ = ( 5 - y ) / ( 7 - x )
m₂ = 2
On simplifying , we get
( 5 - y ) / ( 7 - x ) = 2
Multiply by ( 7 - x ) , we get
5 - y = 14 - 2x
Adding 2x and subtracting 5 on both sides , we get
2x - y = 9
Substitute the value of x from m₁ , we get
2 ( 2y ) - y = 0
3y = 9
Divide by 3 on both sides , we get
y = 3
And , the value of x = 6
Hence , the coordinate of the point P is P ( 6 , 3 )
To learn more about equation of line click :
https://brainly.com/question/14200719
#SPJ9
julia needs to make 500 hamburgers for the a school function... hamburger patties are sold in packets of 12
how many packets of patties should she buy ?
Answers
Julia needs to buy 42 packets of patties to make 500 hamburgers for the school function
What is an equation?An equation is an expression that shows how two or more numbers and variables are related using mathematical operations of addition, subtraction, multiplication, division, exponents and so on.
Hamburger patties are sold in packets of 12. Let x represent the number of packet of patties to be bought to make 500 hamburgers. Hence:
12x = 500
x = 500/12
x = 41.67
x≅ 42
Julia needs to buy 42 packets
Find more on equation at: https://brainly.com/question/2972832
#SPJ1
In the figure below, $ABDC,$ $EFHG,$ and $ASHY$ are all squares; $AB=1$, $EF=1$, and $AY=5$. What is the area of quadrilateral $DYES$? [asy] size(5cm); defaultpen(black+1); pair a=(0,5); pair b=(1,5); pair c=(0,4); pair d=(1,4); pair e=(4,1); pair f=(5,1); pair g=(4,0); pair h=(5,0); pair y=(0,0); pair s=(5,5); draw(a--s--h--y--a); draw(c--d--b,gray); draw(g--e--f,gray); draw(d--y--e--s--d); dot(a); dot(b); dot(c); dot(d); dot(e); dot(f); dot(g); dot(h); dot(y); dot(s); label("$A$",a,NW); label("$B$",b,N); label("$C$",c,W); label("$D$",d,SE); label("$E$",e,NW); label("$F$",f,E); label("$G$",g,S); label("$H$",h,SE); label("$Y$",y,SW); label("$S$",s,NE); [/asy]
Answers
Since $ASHY$ is a square and $AY=5$, we have $AS=SY=5\sqrt{2}$. Since $ABDC$ is a square and $AB=1$, we have $AC=\sqrt{2}$, so $CY=5\sqrt{2}-\sqrt{2}=4\sqrt{2}$. Finally, since $EFHG$ is a square and $EF=1$, we have $EG=GF=1\sqrt{2}$.
[asy] size(6cm); defaultpen(black+1); pair a=(0,5); pair b=(1,5); pair c=(0,4); pair d=(1,4); pair e=(4,1); pair f=(5,1); pair g=(4,0); pair h=(5,0); pair y=(0,0); pair s=(5,5); draw(a--s--h--y--a); draw(c--d--b,gray); draw(g--e--f,gray); draw(d--y--e--s--d); dot(a); dot(b); dot(c); dot(d); dot(e); dot(f); dot(g); dot(h); dot(y); dot(s); label("$A$",a,NW); label("$B$",b,N); label("$C$",c,W); label("$D$",d,SE); label("$E$",e,NW); label("$F$",f,E); label("$G$",g,S); label("$H$",h,SE); label("$Y$",y,SW); label("$S$",s,NE); label("$1$",(a+b)/2,N); label("$\sqrt{2}$",(c+d)/2,N); label("$1\sqrt{2}$",(e+f)/2,N); label("$5$",(a+s)/2,W); label("$5$",(s+h)/2,E); label("$5\sqrt{2}$",(a+s)/2,NE); label("$5\sqrt{2}$",(s+h)/2,NW); label("$4\sqrt{2}$",(s+y)/2,NW); [/asy]
We can now compute the area of quadrilateral $DYES$ by subtracting the areas of triangles $DYE$ and $YES$ from the area of square $DESY$.
We have $[DYE]=\frac{1}{2}\cdot DY\cdot YE=\frac{1}{2}\cdot(4\sqrt{2})\cdot(5\sqrt{2}-1)=38-2\sqrt{2}$ and $[YES]=\frac{1}{2}\cdot YS\cdot ES=\frac{1}{2}\cdot(5\sqrt{2})\cdot(1\sqrt{2})=\frac{25}{2}$.
The area of square $DESY$ is $(DY+YE)^2=(4\sqrt{2}+5\sqrt{2}-1)^2=100-18\sqrt{2}$. Thus, the area of quadrilateral $DYES$ is \begin{align*}
[DESY]-[DYE]-[YES]&=\left(100-18\sqrt{2}\right)-\left(38-2\sqrt{2}\right)-\left(\frac{25}{2}\right)\
&=61-\frac{49}{2}\sqrt{2}.
\end{align*}Therefore, the area of quadrilateral $DYES$ is $\boxed{61-\frac{49}{2}\sqrt{2}}$.
During week 1 of a recycling drive, the fifth grade class recycled 9
pounds of glass and 123 pounds of newspaper. During week 2, the
fifth grade class recycled 8 pounds of glass and 13 pounds of
newspaper. How many more pounds of newspaper than glass did
the class recycle?
Answers
Answer:
119 pounds
Step-by-step explanation:
Glass :
1) 9 pounds
2) 8 pounds
9 + 8 = 17 pounds
Newspaper
1) 123 pounds
2) 13 pounds
123 + 13 = 136 pounds
136 - 17 = 119 pounds
{1, √2, √√3, 2, √5, ...}
need help knowing the sequence and the 3 next terms
Answers
Answer:
3, 2√2, √7
Step-by-step explanation:
compute the square roots of the next three prime numbers:
√7
√11
√13
Therefore, the next three terms of the sequence are:
{1, √2, √3, 2, √5, √7, √11, √13}
chatgpt
chat
Test Practice When Xavier buys his lunch, he saves the nickel
gets as change. How much money will Xavier have if he buys his
lunch 4 times one week and 2 times the second week?
Answers
Understanding:
First of all, each time Xavier buys lunch he saves a nickel. That means if he buys lunch twice, he is saving 2 nickels, buys 3 times he saves 3 nickels, and so on. To solve this problem we can simply add the times he bought lunch and that will equal the value of nickles he saved so far.
Solution:
First-week savings = 4 nickels
Second-week savings = 2 nickels
Simply, adding those together gives us 6 nickels.
Malcolm has $50 gift card to a local car wash and order is the ultimate car wash each visit is $8.95
Answers
The amount cheaper is the car washes Malcolm orders than the car washes Martha's order is $13.
The correct answer choice is option B.
How much cheaper is the car washes Malcolm orders than the car washes Martha's order?Malcolm's gift card = $50.
Cost Malcolm's car wash per visit = $7
Martha's gift card = $180
Cost Martha's car wash per visit = Difference between gift card balance of first and second visit
= $180 - $160
= $20
How cheap is the car washes Malcolm orders than the car washes Martha's order = $20 - $7
= $13
Therefore, Malcolm's car wash is cheaper than Martha's car wash by $13
The complete question is attached in the diagram.
Read more on graphs:
https://brainly.com/question/19040584
#SPJ1

The sum of 3 times the value of x and 2 is equal to 4 less than 5 times the value of x. Which equation can be used
to find the value of x2
3x + 2 4 - 5x
62% + 3 = 4 -5%
3x + 25% - 4
None of these
Answers
Answer:
3x + 2 4 5x
Step-by-step explanation:
The solution of the equation formed 3x + 5x = 4 - 2 will be; x = 1/4.
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables.
We have given that sum of 3 times the value of x and 2 is equal to 4 less than 5 times the value of x then;
The sum of 3 times the value of x and 2 means (3x + 2)
4 less than 5 times the value of x means (4 - 5x)
Therefore, the equation would be;
3x + 2 = 4 - 5x
Now solving for x;
3x + 5x = 4 - 2
8x = 2
x = 1/4
Hence, the solution of the equation formed 3x + 5x = 4 - 2 will be; x = 1/4.
Learn more about equations here;
https://brainly.com/question/25180086
#SPJ2
Three animals left 24 tracks in the mud. Half the tracks were made by either a dog or a fox. A deer made 4 tracks fewer than the dog and 4 tracks more than the fox. How many tracks did each animal leave?
Answers
The deer made 8 tracks, the fox made 4 tracks, and the dog made 12 tracks.
How to find the number of tracks each animal madeLet's start by defining variables for the number of tracks made by each animal.
Let:
d be the number of tracks made by the deer,
f be the number of tracks made by the fox, and
x be the number of tracks made by the dog
From the problem, we know that:
d + f + x = 24 ......(1)
We also know that:
d = x - 4 .......(2)
d = f + 4 ..........(3)
from this we can rightfully assume that the dog made half the tracks hence
x = 12 tracks
d = 12 - 4 = 8
solving for f
d = f + 4
f = d - 4 = 8 - 4 = 4
we can therefore say that the dog made 12 tracks, the deer made 8 tracks while the fox made 4 tracks
Learn more about word problems at:
https://brainly.com/question/13818690
#SPJ1
Find the value of k to the nearest whole number.
Answers
Answer:
theres no picture or something for the value of k
Please help me. Expert only. Right answer only.

Answers
Answer:
241.2
Step-by-step explanation:
Divide 201 by 10
\(201/10=20.1\)
Multiply 20.1 by 12
\(20.1 * 12 = 241.2\)
The answer is 241.2
MC1103: A travel agent books passages on three different tours, with half of her customers choosing tour T1, one-third choosing tour T2, and the remaining one-sixth choosing tour T3. The agent has noted that 3/4 of those who take T1 return to book passage again, 2/3 of those who take T2 return, and 1/2 of those who take T3 return. If a customer does return, what is the probability that the person first went on tour T2
Answers
Using conditional probability, it is found that there is a 0.3266 = 32.66% probability that the person first went on tour T2.
Conditional Probability
\(P(B|A) = \frac{P(A \cap B)}{P(A)}\)
In which
P(B|A) is the probability of event B happening, given that A happened. \(P(A \cap B)\) is the probability of both A and B happening. P(A) is the probability of A happening.In this problem:
Event A: Customer returns.Event B: Customer first went on tour T2.The percentages associated with a return are:
3/4 = 0.75 of 0.5(choosing T1).2/3 = 0.6667 of 1/3 = 0.3333(choosing T2).1/2 = 0.5 of 1/6 = 0.1667(choosing T3).Hence:
\(P(A) = 0.75(0.5) + 0.667(0.3333) + 0.5(0.1667) = 0.6806611\)
The probability of both returning and first going on T2 is:
\(P(A \cap B) = 0.667(0.3333)\)
Hence, the conditional probability is:
\(P(B|A) = \frac{P(A \cap B)}{P(A)} = \frac{0.667(0.3333)}{0.6806611} = 0.3266\)
0.3266 = 32.66% probability that the person first went on tour T2.
A similar problem is given at https://brainly.com/question/14398287
Someone help me please

Answers
Answer:
y=4
Step-by-step explanation:
The triangle on the right is a 30-60-90 triangle
The ratio of sides in a 30-60-90 triangle is 1:√3:2
y:x:8
SO y will be 4 because 8/y=2/1
What is the volume and surface are of a right circular cylinder with a diameter of 14 meters and a height of 9 meters
Answers
Answer: V≈1385.44m
Step-by-step explanation: V=π(d2)2h=π·(142)2·9≈1385.44236m³
Help me pleaseeeeeeeee
8(x-6)+58=-3(2x-8)+14x
THANK YOU!!!!!!!!!!
Answers
Second rearrange unknown terms to the left side of the equation: 8x+6x-14x=24+48-58
Third combine like terms: 0=24+48-58
Fourth calculate sum: 0=14
In conclusion there is no solution to this equation. Please give brainliest because this was a b11tch to type :)
Answer:
10 = 24
Step-by-step explanation:
\(8(x - 6) + 58 = - 3(2x - 8) + 14x\)
\(8x - 48 + 58 = - 6x + 24 + 14x\)
\(8x + 10 = 8x + 24\)
\(10 = 24\)
x €\( \O\)