Answers
Answer:
D) (x,y) → (x+4, y-6)
Step-by-step explanation:
Explanation:-
Given that the points are X(2,3), Y(5,6), and Z(8,6)
The vertical translation down 'd' units then transformed to
(x,y) → (x, y-d)
The vertical translation down '6' units then transformed to
(x,y) → (x, y-6)
X(2,3)→ X¹( 2, 3-6)
Y(5,6)→Y¹(5,6-6)
Z(8,6)→Z¹(8,6-6)
Again
The Horizontal translation 'c' units right then transformed to
(x,y) → (x+C, y-d)
The Horizontal translation '4' units right then transformed to
(x,y) → (x+4, y-6)
The new co-ordinates
X(2,3)→ X¹( 2+4, 3-6)→X¹(6,-3)
Y(5,6)→Y¹(5+4,6-6)→ Y¹(9,0)
Z(8,6)→Z¹(8+4,6-6)→Z¹(12,0)
Final answer:-
The new co-ordinates are
X¹(6,-3) ,Y¹(9,0), Z¹(12,0)
Related Questions
An airplane is traveling at a speed of 200 miles/hour with a bearing of 240°. The wind velocity is 60 miles/hour at a bearing of 25°. What are the
plane's actual speed and direction angle?
Answers
Answer:
225.1°
155mph
What is exponential form examples?
Answers
Exponential form is a way of representing repeated multiplications of the same number by writing the number as a base with the number of repeats written as a small number to its upper right.
In the exponential form, the exponent indicates the number of times the base is used as a factor.
For example, in the case of 16 it can be written as 2 × 2 × 2 × 2 = \(2^{4}\), where 2 is the “base” and 4 is the “exponent.
A product in which the factors are identical is called a power of that factor. The number that is repeated is called the base, and the number of times it repeats is called the exponent, power or degree. And the power that is written on the right upper side are called exponents. when multiplying the numbers having same base and different exponents then the base is kept same and the exponents are added.
To learn more about Exponential form please visit:
https://brainly.com/question/23275698
#SPJ4
Describe the transformation from f(x) to g(x) if the black parabola represents f(x)=x2 and the purple parabola is g(x) .

Answers
ANSWER:
Shift 3 units left and 4 units down
STEP-BY-STEP EXPLANATION:
The function g(x) is located in the third quadrant, that is, in the quadrant that is down and to the left.
We can carefully observe that the translation was 3 units to the left and 4 units down.
Write a system of linear equations in which (2, -1) is a solution of equation 1 but
not a solution of equation 2, and (5, 5) is a solution of the system. then solve the
system by substitution to verify that (5, 5) is the solution.
Answers
The sytem of liner equation are that satisfies the given conditon are:
L1 : 2x-y=5
L2 : 3x - y = 10
Given that one of the line of the sytem of equations passes through (2,-1) and also given that solution of system of equations is (5,5) so it justifies that the 1st line passes through (2.-1) and (5,5) so the equation of 1st line is given by:
To find the equation of a line that passes through the points (2, -1) and (5, 5), we can use the point-slope form of a line, which is:
y - y1 = m(x - x1)
where (x1, y1) is a point on the line, and m is the slope of the line.
To find the slope of the line, we can use the formula:
m = (y2 - y1) / (x2 - x1)
Substituting the coordinates of the two given points and the formula for the slope into the point-slope form, we get:
y - (-1) = ((5 +1) / (5 - 2))(x - 2)
= (6 / 3)(x - 2)
= 2(x - 2)
= 2x - 4
=> 2x- y =5
so the equation of line 1 is 2x-y=5
And as mentioned that equation of line that passes through (5,5) but as given it won't pass through (2,-1)
so let m be the slope of 2nd line and passes through (5,5)
so the equation of line is given by:
y-5 = m (x-5)
and if this line won't pass through (2,-1) then
-1 - 5 ≠ m (2 -5)
m ≠ 2
so the equation of 2nd line is given by:
y - 5 = 3(x-5)
=> 3x - y = 10
So the equation of sytem of liner equation are
L1 : 2x-y=5
L2 : 3x - y = 10
To know more about linear equation click on below link:
https://brainly.com/question/11897796#
#SPJ4
1b) Determine the measure of the unknown angle.
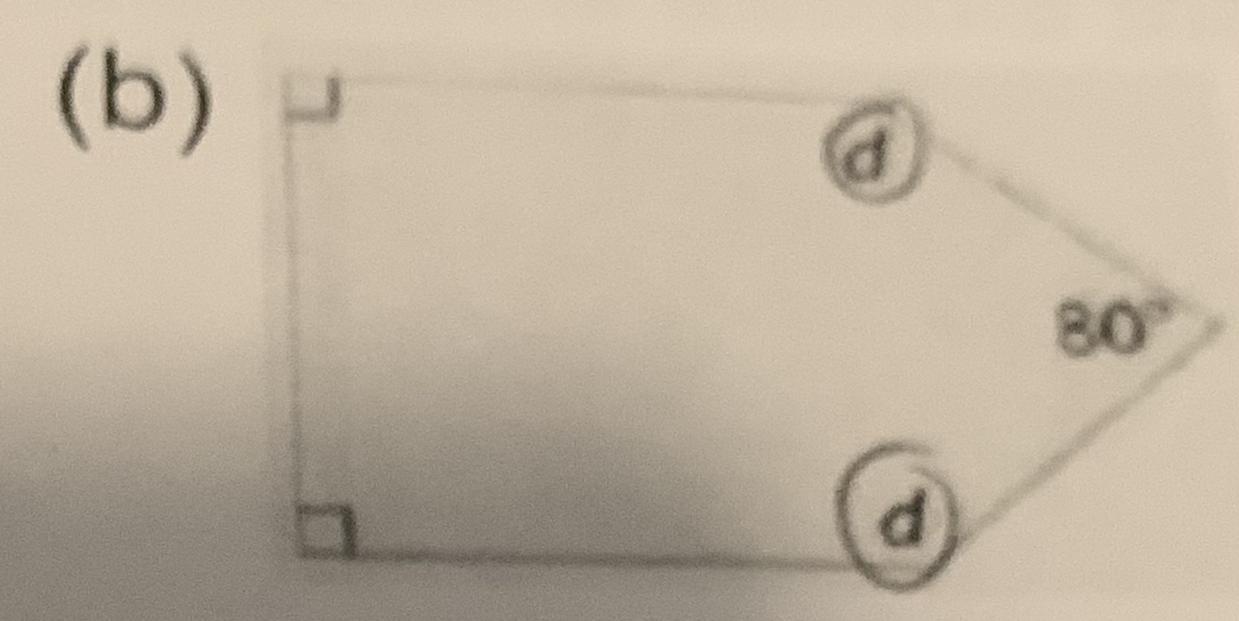
Answers
working : 540° - 90° -90° -80°= 280°
280/2 =140°
A train travelling at 20 m/s stops in 40 seconds. What is the acceleration of the train (numeric answers only - no units)
Answers
The equation of motion we will use is
\(v=u+at\)Where
v is the final velocity
u is the initial velocity
a is the acceleration
t is the time
From the problem, we can figure out that the starting velocity, u, is 20. The time, t, is 40. The final velocity, v, will be 0.
Substituting, let's figure out acceleration, a :
\(\begin{gathered} v=u+at \\ 0=20+a(40) \\ 0=20+40a \\ 40a=-20 \\ a=-\frac{20}{40} \\ a=-\frac{0.5m}{s^2} \end{gathered}\)The acceleration is negative because it is deceleration.
Here are two rectangular prisms: K, L. K= 6, 4, 5. L=5,5,5 1. Which figure do you think has the longer diagonal. 2. Calculate the lengths of both diagonals. Which one is actually longer?
Answers
Answer:
sorry. I need points.
Step-by-step explanation:
.......................
Un concensario de coches rebaja a 16000 un vehiculo que valia 18300 en que porcentaje lo han rebajado?
Answers
As a car dealer lowers a vehicle that was worth 18300 to 16000 by applying the formula of change in percentage we get that by 12.569 percentage (approximately) the price gets lowered .
The initial price of the car is set at P = 18300 (units)
The price after lowering drom P becomes A= 16000 (units)
Hence the change in price (or value) of the car, that is the price of the car is lowered by, C = (initial price - lowered price) = (P - A) = (18300 - 16000) units = 2300 units.
The formula for calculating percentage change is given as follows,
Change in percentage = [(Change in value)/ ( Initial value) ]*100
⇒Change in percentage = (C/ P)*100
⇒ Change in percentage =( 2300/ 18300)*100 = 12.569% (approximately)
To know more about change iin percentage here
https://brainly.com/question/14801224
#SPJ4
a television program director has 14 shows available for monday night but can choose only 5 shows. how many different possible combinations are there?
Answers
There are 240240 possible permutations of choosing 5 shows from 14 available shows. It can be obtained by applying the formula of permutation.
What is permutation?
In mathematics, it is the number of ways in which given number of items can be arranged in different orders.
Here, we need to select 5 iteams from the given 14 iteams.
\(P(14,5)=\frac{14!}{(14-5)!}\\=\frac{14!}{(9!)}\\=\frac{(14)(13)(12)(11)(10)(9!)}{(9!)}\\=(14)(13)(12)(11)(10)\\=240240\)
Hence, there are 240240 possible permutations of choosing 5 shows from 14 available shows.
Learn more about permutation from the following link:
https://brainly.com/question/12468032
#SPJ4
1. What is the circumference of a circle with a radius of 5 inches? Leave your
answer in terms of pi.
A = xr2
C = 21

Answers
Answer:
Option 1 = 10pi
Step-by-step explanation:
Formula-2•radius•pi
2•5•pi
10 pi
nate has a grid made of shaded and unshaded 2 cm by 2 cm squares, as shown. he randomly places a circle with a diameter of 3 cm on the board so that the centre of the circle is at the meeting point of four squares. the probability that he places the disk so that it is touching an equal number of shaded and unshaded squares is ab. what is a b ?
Answers
The value of a and b is 1.
THE PROBABILITY OF A AND BThe probability that Nate places the disk so that it is touching an equal number of shaded and unshaded squares is ab, where a and b are integers.
To find the value of a and b, we need to determine the total number of ways Nate can place the disk (the denominator of the probability fraction) and the number of ways he can place the disk so that it touches an equal number of shaded and unshaded squares (the numerator of the probability fraction).
Since the center of the circle must be at the meeting point of four squares, the only possible places for the center are the points where four squares meet. Since the grid is made of 2 cm x 2 cm squares, there are 4 shaded squares and 4 unshaded squares. So, there are 4 centers that could be placed on a shaded square and 4 centers that could be placed on an unshaded square.
So the denominator of the probability fraction is 8.
Now, to calculate the numerator, we need to determine the number of ways Nate can place the disk so that it touches an equal number of shaded and unshaded squares.
As the center of the circle is at the meeting point of four squares, the center of the circle is placed at the intersection of 2 shaded and 2 unshaded squares.
So, the numerator of the probability fraction is 8.
Therefore, the probability that Nate places the disk so that it is touching an equal number of shaded and unshaded squares is 8 ÷ 8 =1.
So the value of a and b is 1.
Learn more about Probability here:
https://brainly.com/question/11234923
#SPJ4
use a linear approximation (or differentials) to estimate the given number.
Answers
Using linear approximation, the estimated distance the boat will coast is approximately 266 feet. (Rounded to the nearest whole number.)
To estimate the distance the boat will coast using a linear approximation, we can consider the average velocity over the given time interval.
The initial velocity is 39 ft/s, and 9 seconds later, the velocity decreases to 20 ft/s. Thus, the average velocity can be approximated as:
Average velocity = (39 ft/s + 20 ft/s) / 2 = 29.5 ft/s
To estimate the distance traveled, we can multiply the average velocity by the time interval of 9 seconds:
Distance ≈ Average velocity * Time interval = 29.5 ft/s * 9 s ≈ 265.5 ft
Using linear approximation, we estimate that the boat will coast approximately 266 feet.
To learn more about number, click here:
brainly.com/question/3589540
#SPJ1
A population has a mean of 180 and a standard deviation of 36. A sample of 84 observations will be taken. The probability that the sample mean will be between 181 and 185 is?.
Answers
The probability that the sample mean will be between 181 and 185 is 0.3039.
Given,
The mean of a population, μ = 180
Standard deviation, σ = 36
Number of sample observations, n = 84
We have to find the probability that the sample mean will be between 181 and 185;
Lets convert 181 and 185 into z scores;
z = (x - μ) / (σ/√n)
x = 181z = (181 - 180) / (36/√84)
z = 1/3.93
z = 0.25
x = 185z = (185 - 180) / (36/√84)
z = 5 / 3.93
z = 1.27
Lets look z score table;
The area to the left of z = 0.25 is 0.5987
The area to the left of z = 1.27 is 0.8980
The probability that the z is between 0.25 and 1.27 would be 0.8980 – 0.5887 = 0.3039.
That is,
The probability that the sample mean will be between 181 and 185 is 0.3039.
Learn more about probability here;
https://brainly.com/question/6598268
#SPJ4
I WILL MARK BRAINLIEST IF CORRECT! Pls also give an explanation!
The sides of a square are 4 units long. One vertex of the square is located at (-1,1) on the standard (x,y) coordinate plane. Which of the following points could also be a vertex of the square?
a. (-3,3)
b. (-5,-3)
c. (3,3)
d. (-5,3)
e. (4,5)

Answers
Answer:
There is no solution (since none has side length of 4 units)
Step-by-step explanation:
If V (-1,1) is one of vertex of a square, then the next vertex to V distance must be the known value of 4
VA: V to (-3,3) = √(-1 - -3)² + (1 - 3)² = √8 = 2.8
VB: to (-5,-3) = √(-1 - -5)² + (1 - -3)² = √32 = 5.7
VC: o (3,3) = √(-1 -3)² + (1 - 3)² = √20 = 4.47
VD: to (-5,3) = √(-1 - -5)² + (1 - 3)² = √20 = 4.47
VE: to (4,5) = √(-1 - 4)² + (1 - 5)² = √41 = 6.4
Armando has $25 to spend. he wants to buy 2 pounds of hamburgers at $3 per pound, a bag of buns for $2, and 5 bags of chips for $4 each. Sort each statement into True or False.

Answers
Answer:
True- She needs $3 more. She will not have enough money to buy everything. The cost is $28.
False- She has $3 left over.
Step-by-step explanation:
2 pounds of burgers for $3 each is $6
1 bag o bun equals $2
5 bags of chips for $4 each is $20
$20 + $6 +$2 = $28
She only had $25 to spent, so she doesn't have enough money and needs to 3 more dollars.
another easy trig question

Answers
Answer:
X= 5.44 y= 17.85
Step-by-step explanation:
Given that your B angle is 60 degress you can use 17tan(60) to get X which is 5.44.
Then you a²+b²=c² to find y.
y=√17²+5.44²
y= 17.85
Answer: X= 5.44 y= 17.85
Hope this helps
What is the slope-intercept form of the function described by this table? x 1 2 3 4 y 8 13 18 23 Enter your answer by filling in the boxes. y = x +
Answers
Answer:
y = 5 x + 3
Step-by-step explanation:
I took the quiz
5,2,4/5 find the 10th term
Answers
512/390625
SOMEONE PLEASE HELP QUICKLY I WILL GIVE BRAINLIEST TO THE QUICKEST ANSWER
A two-digit locker combination is made up of two non-zero digits. Digits in
a combination are not repeated and range from 3 through 8.
Event A = choosing an odd number for the first digit
Event B = choosing an odd number for the second digit
If a combination is chosen at random, with each possible locker
combination being equally likely, what is P(A and B) expressed in simplest
form?
Answers
Answer:
1/6
Step-by-step explanation:
You are given n = 8 measurements: 4, 4, 7, 6, 4, 6, 6, 8. (a) Calculate the range. 4 (b) Calculate the sample mean, x. x=5625 (c) Calculate the sample variance, s2, and standard deviation
Answers
(a)The range of the given set of measurements is 4.
(b)The sample mean of the given set of measurements is approximately 5.625.
(c)The sample variance of the given set of measurements is approximately 2.337768, and the sample standard deviation is approximately 1.529.
(a) The range is the difference between the largest and smallest values in the set of measurements. In this case, the largest value is 8 and the smallest value is 4, so the range is 8 - 4 = 4.
To calculate the range, we subtract the smallest value from the largest value. In this case, the largest value is 8 and the smallest value is 4.
Range = Largest value - Smallest value
Range = 8 - 4
Range = 4
The range provides a simple measure of the spread or dispersion of the data. In this case, the range tells us that the values range from the smallest value of 4 to the largest value of 8, with a difference of 4 between them.
(b) The sample mean, denoted as x, is the sum of all the measurements divided by the total number of measurements.
To calculate the sample mean, we add up all the measurements and then divide by the total number of measurements. In this case, we have 8 measurements.
Sum of measurements = 4 + 4 + 7 + 6 + 4 + 6 + 6 + 8 = 45
Sample mean = Sum of measurements / Total number of measurements
Sample mean = 45 / 8
Sample mean ≈ 5.625
The sample mean represents the average value of the measurements and provides a measure of central tendency.
(c) The sample variance, denoted as s^2, measures the variability or dispersion of the data points around the sample mean. It is calculated as the average of the squared differences between each measurement and the sample mean.
To calculate the sample variance, we first calculate the squared difference between each measurement and the sample mean. Then, we average those squared differences.
Squared difference for each measurement:
(4 - 5.625)^2 = 2.890625
(4 - 5.625)^2 = 2.890625
(7 - 5.625)^2 = 1.890625
(6 - 5.625)^2 = 0.140625
(4 - 5.625)^2 = 2.890625
(6 - 5.625)^2 = 0.140625
(6 - 5.625)^2 = 0.140625
(8 - 5.625)^2 = 5.390625
Sum of squared differences = 2.890625 + 2.890625 + 1.890625 + 0.140625 + 2.890625 + 0.140625 + 0.140625 + 5.390625 = 16.364375
Sample variance = Sum of squared differences / (Total number of measurements - 1)
Sample variance = 16.364375 / (8 - 1)
Sample variance ≈ 2.337768
The standard deviation, denoted as s, is the square root of the sample variance.
Sample standard deviation = √(Sample variance)
Sample standard deviation = √(2.337768)
Sample standard deviation ≈ 1.529
These measures provide information about the dispersion or spread of the data points around the sample mean. A higher variance or standard deviation indicates greater variability in the measurements.
To know more about standard deviation, visit;
https://brainly.com/question/31516010
#SPJ11
A 4-foot long steel pipe consists of two concentric cylinders, with the inner cylinder hollowed out. The radius of the outside of the pipe is 6 inches and the radius of the inside of the pipe is 5.75 inches.
A. Determine the volume of metal used to build the pipe
B. If the pipe is to be powder-coated on the inside and outside surfaces, what is the total surface area to be powder-coated?

Answers
Answer:
Step-by-step explanation:
The radius of the outside of the pipe is 6 inches and the radius of the inside of the pipe
is 5.75 inches
Determine the volume of metal used to build the pipe.
How well a system is accepted by the users and incorporated into the ongoing operations of the business is defined in the technical feasibility.
Answers
technical feasibility is concerned with evaluating the technological aspects of a proposed project, assessing available resources, and determining if the project can be successfully implemented within the given constraints. It does not directly address user acceptance or incorporation into ongoing business operations, which fall under other aspects such as operational feasibility or organizational feasibility.
Technical feasibility is the evaluation of whether a proposed solution is capable of being developed with available technology and within budgetary and schedule constraints. It assesses the technical resources available in the business and the extent to which the proposed project may be developed from a technical standpoint.
A technical feasibility study focuses on the cost, time, and complexity of the project. It aims to identify and examine the factors that would help or hinder the implementation of the proposed system. This study determines whether the proposed system is achievable within the constraints of available technology, budget, and resources.
To achieve technical feasibility, the project should be analyzed from various angles, such as software, hardware, manpower, and location. It answers the question of whether the project is feasible in terms of the available technology. If the required technology is available, the project can be implemented; otherwise, it will not be feasible.
In summary, technical feasibility is concerned with evaluating the technological aspects of a proposed project, assessing available resources, and determining if the project can be successfully implemented within the given constraints. It does not directly address user acceptance or incorporation into ongoing business operations, which fall under other aspects such as operational feasibility or organizational feasibility.
To know more about technical feasibility
https://brainly.com/question/14009581
#SPJ11
Use Taylor polynomial approximation to avoid loss-of-significance error in the following formula when x is near 0 . The polynomial should be degree 6 , not counting the remainder term. Write the remainder term, but you do not need to estimate it. x3x−sin(x)
Answers
To use Taylor polynomial approximation to avoid loss-of-significance error in the formula x^3 * x - sin(x) when x is near 0, we can first find the Taylor polynomial of degree 6 for the function.
P(x) = f(a) + f'(a)(x-a) + (f''(a)(x-a)^2)/2! + (f'''(a)(x-a)^3)/3! + ... + (f^(n)(a)(x-a)^n)/n!
where f(a) represents the function value at the point a, and f^(n)(a) represents the nth derivative of the function evaluated at a.
For the given function, we have:
f(x) = x^3 * x - sin(x)
Taking the derivatives of f(x), we have:
f'(x) = 4x^3 - cos(x)
f''(x) = 12x^2 + sin(x)
f'''(x) = 24x - cos(x)
To find the Taylor polynomial of degree 6, we need the function values and derivatives evaluated at x = 0:
f(0) = 0
f'(0) = 0
f''(0) = 0
f'''(0) = 0
Using these values in the Taylor polynomial formula, we get:
P(x) = 0 + 0(x-0) + 0(x-0)^2/2! + 0(x-0)^3/3! + 0(x-0)^4/4! + 0(x-0)^5/5! + 0(x-0)^6/6!
Simplifying the polynomial, we have:
P(x) = 0
To know more about avoid visit :
https://brainly.com/question/30637335
#SPJ11
Find the area. Leave your answer in simple radical form.

Answers
Therefore, the area of the pentagon is 928 square units.
lengthLength is a measure of the size or extent of an object or a distance between two points. It refers to the longest dimension of an object or the distance between two points in space, typically measured in units such as inches, centimeters, meters, or miles. In mathematics, length is also used to describe the size of a line segment or a curve, which can be measured using various techniques such as Euclidean distance, arc length, or fractal dimension. Length is an important concept in many fields, including physics, engineering, geometry, and statistics.
Find the area.
Pentagon
apothem = 16 side = 23.2
Note: When necessary, enter your answer as a decimal If it is not a terminating decimal, round to the nearest hundredth
For the first question, we need more information to find the area of the triangle. Knowing the apothem and one side is not enough. We also need to know the number of sides of the triangle or the length of another side or the height.
For the second question, the formula to find the area of a regular pentagon is:
Area = (perimeter x apothem)/2
Since we are given the apothem and the side, we can find the perimeter of the pentagon as:
perimeter = 5 x side = 5 x 23.2 = 116
Substituting the values in the formula, we get:
Area = (116 x 16)/2 = 928
Therefore, the area of the pentagon is 928 square units.
To know more about perimeter visit:
https://brainly.com/question/9369181
#SPJ1
You have just inherited $150,261 from a trust that has matured. you would like to invest the total amount into an account that pays you an annual compounded interest rate of 9.1%, and you would like to make annual withdrawals over the next 20 years such that by the end of this 20 year period, the amount remaining in the account will be zero dollars. determine, from the given information, the amount of the annual withdrawals. round to the nearest cent. a. $16,578.03 c. $15,978.10 b. $162,851.31 d. $15,575.98
Answers
The amount of the annual withdrawals will be $16,574.24.The amount is the sum of the principal and the simple interest gain.
What is the amount?The complete repayment of money at the end of the time period for which it was borrowed is referred to as the amount.
The given data in the problem is;
P ia the annual payment
PV is the present value = $150,261
r is the rate of intreast = 9.1% = 0.091
n is the time period= 20
The formula for the annual payment is found as;
\(\rm P= \frac{r \times PV}{1-(1+r)^{-n}} \\\\ \rm P= \frac{0.091 \times 150261}{1-(1+0.091)^{-20}} \\\\ \rm P=16,754.2437\)
Hence the amount of the annual withdrawals will be $16,574.24.
To learn more about the amount refer to the link;
https://brainly.com/question/12184047
.........................

Answers
Hey there!
The answer is D
We solve this by multiplying the exponents, and we get 15:
3 x 5 = 15
So, the answer is 2^15
Hope it helps and have a great day!
What is the length of side x in a 30-60-90 triangle where one side is the square root of 3 and the other side is unknown?
Answers
Answer:
The length of side x in a 30-60-90 triangle is 2√3.
Step-by-step explanation:
The numbers 30-60-90 are angles, so we need to find the side x of a right triangle with the following information:
θ: is one angle of the right triangle = 30°
α: is the other angle of the right triangle = 60°
a: is one side of the right triangle = √3
b: is the other side of the right triangle =?
x: is the hypotenuse of the right triangle =?
The length of the hypotenuse can be found by Pitagoras:
\( x^{2} = a^{2} + b^{2} \) (1)
So, we need to find the side "b". We can calculate it with the given angles.
From the side "a" we have:
\( cos(\alpha) = \frac{a}{x} \)
\( cos(60) = \frac{\sqrt{3}}{x} \) (2)
From the side "b":
\( sin(\alpha) = \frac{b}{x} \)
\( sin(60) = \frac{b}{x} \) (3)
Now, we can calculate "b" by dividing equation (3) by equation (2).
\( tan(60) = \frac{\frac{b}{x}}{\frac{\sqrt{3}}{x}} \)
\( b = tan(60)*\sqrt{3} = 3 \)
Finally, we can find the length of the hypotenuse with equation (1):
\( x = \sqrt{a^{2} + b^{2}} = \sqrt{(\sqrt{3})^{2} + (3)^{2}} = 2\sqrt{3} \)
Therefore, the length of side x in a 30-60-90 triangle is 2√3.
I hope it helps you!
Use the grouping method to factor this polynomial.
3+2x2 +7 x + 14
Answers
Answer:
7 ( x + 3 )
Step-by-step explanation:
Use order of operations to multiply first.
3+2x2 +7 x + 14
3+4 +7 x + 14
Now group like terms.
3+ 7x + 4 + 14
Add like terms
7x + 21
Find the two multiples of 21.
7x + 7 x 3
Now factor out the 7.
7( x + 3 )
2 1/2 = 5n
I need help please
Answers
Answer:
1/2
Step-by-step explanation:
because 5 times 1/2 and you get 2 1/2
Convert 500kg to lbs
Answers
We can use the fact that 1 pound is equal to 0.45359237 kg and then convert it to kg first and then divide it by 0.45359237 kg/lb. So, 500 kg / 0.45359237 kg/lb = 1102.31 lbs
To convert a weight from kilograms (kg) to pounds (lbs), you need to know the conversion factor between the two units.
The conversion factor between kilograms and pounds is 1 kilogram = 2.20462 pounds. To convert a weight in kilograms to pounds, you simply multiply the weight in kilograms by the conversion factor.
To convert 500 kg to lbs, we can use the following calculation:
500 kg * 2.20462 lbs/kg = 1102.31 lbs
For more such questions on Conversion.
https://brainly.com/question/24545553#
#SPJ11
