Terrell gets paid a 5% sales commission on every solar-powered scooter he sells. If each scooter sells for $2,400 and Terrell sold 11 of them in April, how much did he make in sales commissions?
Answers
EXPLANATION
Terrel Commisision = 5% = 0.05 (in decimal form)
Scooter Sale Price = $2,400
Number of sold scooters = 11
He made in commision:
0.05x2400x11= 1,320
The answer is $1,320 in commision
Related Questions
HELP ME OUT PLEASE!!!!!
Answers
Answer:
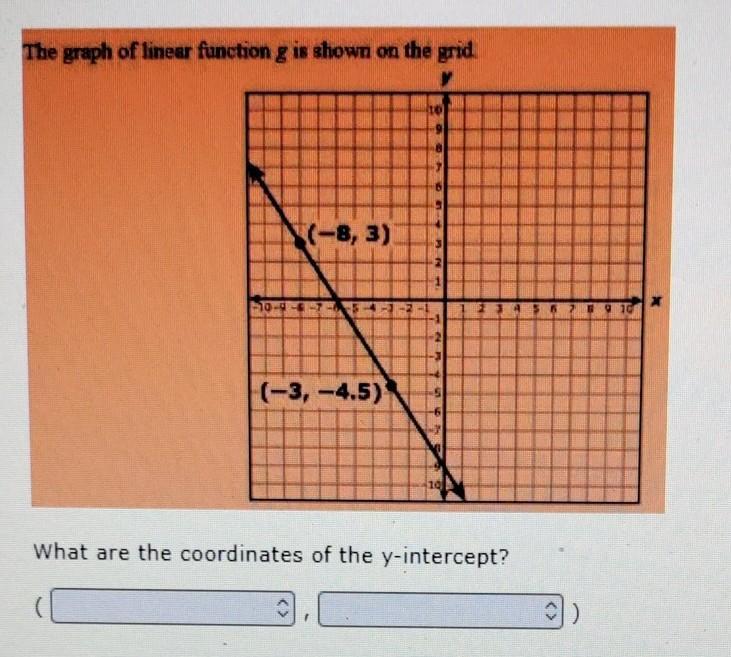
(0 , -9)
Step-by-step explanation:
The y intercept is where the line crosses the y axis.
need help with geometry

Answers
To find the height of the cylinder when the volume is given as 1500 in³ and the radius is 7 inches, we can use the formula for the volume of a cylinder:
Volume = π * r² * h
Substituting the given values, we have:
\(1500 = 3.14 * 7^2 * h1500 = 3.14 * 49 * h1500 = 153.86 * h\)
To solve for h, we divide both sides of the equation by 153.86:
h = 1500 / 153.86
h ≈ 9.75
Rounding the answer to the nearest hundredth, the height of the cylinder is approximately 9.75 inches.
Therefore, the height of the cylinder is 9.75 inches.
Note: It is important to use the accurate value of π, which is approximately 3.14159, for precise calculations. However, in this case, since you specified to use 3.14 for π, I have used that approximation to calculate the height.
For more such questions on volume
https://brainly.com/question/27710307
#SPJ8
solve equation -4m +5=3m-9
pls workings
Answers
Answer:
2
Step-by-step explanation:
- 4m + 5 = 3m - 9
3m - 9 = 5 - 4m
3m + 4m = 5 + 9
7m = 14
m = 14 / 7
m = 2
the volume of a rectangular prism is 10 cubic feet. what could the dimensions of the prism be
Answers
Answer: 2x5x1, 1x10x1 (in any order) and any 3 multiples that make 10
Step-by-step explanation:
Answer:
There are multiple possible sets of dimensions for a rectangular prism with a volume of 10 cubic feet. Here are some possible solutions:
A rectangular prism with dimensions of 1 ft x 2 ft x 5 ft (length x width x height) would have a volume of 10 cubic feet, since 1 x 2 x 5 = 10.
A rectangular prism with dimensions of 2 ft x 1 ft x 5 ft (length x width x height) would also have a volume of 10 cubic feet, since 2 x 1 x 5 = 10.
A rectangular prism with dimensions of 0.5 ft x 1 ft x 20 ft (length x width x height) would also have a volume of 10 cubic feet, since 0.5 x 1 x 20 = 10.
A rectangular prism with dimensions of 5 ft x 1 ft x 2 ft (length x width x height) would have a volume of 10 cubic feet, since 5 x 1 x 2 = 10.
There are infinitely many other possible sets of dimensions for a rectangular prism with a volume of 10 cubic feet.
help please asap i will give you a heart if you do

Answers
Answer:
30
Step-by-step explanation:
2(6)=12
3(6)=18
12+18=30
Step-by-step explanation:
its 30 2(6)=12 3(6)=18
30
-4x = 8
what is it??
Answers
Answer: if your solving for x it’s -2
Step-by-step explanation:
Answer:
x is -2
Step-by-step explanation:
because -4 x -2 is 8
Avery’s younger brother has 18 toy trains and 24 toy cars. He arranged the toys into groups consisting of the same amount of trains and cars with none left over. If he made the greatest number of groups possible, how many groups did he make? *
Answers
Answer:
24?
Step-by-step explanation:
I think it's 24 because if you add 24 and 18, you get 42 and since there are 2 toys, the largest amount of groups you can have is 24.
describe the error. What should the answer should've been?how did they get the wrong answer?

Answers
An absolute value is a distance, then, all the numbers that are absolute values are possitive, as a distance cannot be negaive:
Then,
\(\begin{gathered} \mleft|-x\mright|=x \\ \mleft|-8\mright|=8 \end{gathered}\)Then, the mistake is that the absolute value of -8 is 8 not -8The absolute value of a negative number is the number but possitive.

Which composition of two rigid motions maps ️ABC to ️A'B'C'

Answers
Answer:
C. Translation \((x,y) \longrightarrow (x-7, y+0)\), Reflection in the \(y\)-axis
Multiply. −2(−5)(−3)
Answers
Answer: -30
Step-by-step explanation:
-2 X -5 = 10
10 X -3 = -30
Therefore, -2(-5)(-3) = -30
The multiplication of −2(−5)(−3) is -30
The multiplication of numbers in brackets with negative signs takes a method whereby the signs are taken into account when performing the arithmetic operation.
From the given question, we are to multiply:
= - 2 × (-5) × (-3)
= +10 × (-3)
= -30
Learn more about the multiplication of numbers here:
https://brainly.com/question/1755985
Can someone help me with this math problem asap

Answers
The absolute value function for this problem is given as follows:
y = |x - 4| - 6.
How to define the absolute value function?An absolute value function of vertex (h,k) is defined as follows:
y = a|x - h| + k.
The coordinates of the vertex of the function are given as follows:
(4, -6).
The slope of 1 determines the leading coefficient a as follows:
a = 1.
Hence the function is given as follows:
y = |x - 4| - 6.
More can be learned about absolute value functions at brainly.com/question/3381225
#SPJ1
solve the equation -16=a- 19
Answers
Answer:
a = 3
Step-by-step explanation:
Collect like-terms:
\( - 16 = a - 19\)
\(a = - 16 + 19\)
\(a = 3\)
Answer: 3
Step-by-step explanation: you take 19 from 3 giving you -16
Which statements about the opposite of −12 are true? Select each correct answer. Responses −12 and its opposite are on located on the same side of zero on a number line. negative 12, and its opposite are on located on the same side of zero on a number line. The opposite of −12 is −1/12. The opposite of , negative 12, is , negative fraction 1 over 12, . −12 and its opposite are located the same distance from zero on a number line. negative 12, and its opposite are located the same distance from zero on a number line. The opposite of the opposite of −12 is −12.
Answers
Answer:
The opposite would be +12.
Step-by-step explanation:
In math, an opposite number is the number on the other side of zero on the number line that is the same distance from zero. For example, the number 5 is five spaces from zero on the right-hand side of the number line while the opposite. So the opposite would be -5 because it is five spaces from zero on the left side of a number line.
What is the volume of this cylinder? 40yd 11yd
Use ≈ 3.14 and round your answer to the nearest hundredth.
Answers
Volume of the cylinder is 15197.60(to the nearest hundredth).
What is cylinder?
In mathematics, Cylinder is the basic 3d shapes, which has two parallel circular bases at a distance. The two circular bases are joined by a curved surface, at a fixed distance from the center which is called height of the cylinder.
Given that the radius of the cylinder is 11yd.
and the height of the cylinder is 40yd.
Formula for the volume of cylinder is π × r² × h where π=3.14, r= radius and h= height.
Putting the values we get,
Volume of the cylinder is = 3.14 × (11)² × 40 cubic yd.
= 15197.6
Hence, Volume of the cylinder is 15197.60(to the nearest hundredth).
To know more about cylinder
https://brainly.com/question/16134180
#SPJ1
What is the probability that the two pointers will land on an odd number and letter C? Give the probability as a percent
Answers
Answer:
12.5%
Step-by-step explanation:
hope this helps and its right
Answer:
Your answer would be 12.5%.
Step-by-step explanation:
There are two types of spinners here and the outcome of them is independent. That means
P(odd number, C) = P(odd number) * P(C)
There are two odd numbers out of four numbers in the first spinner. The chance of odd number will be:
P(odd) = 2/(2+2)= 1/2= 50%
There are four letters and the desired outcome is C. The chance for C will be:
P(C) = 1/4= 25%
Then the chance will be:
P(odd number, C) = P(odd number) * P(C)
P(odd number, C) =50% * 25% = 12.5%
Therefore, 12.5% will be your final answer.
Michal got a $50 gift card to an online music store. He bought an $10 album.He wants to buy songs that cost $1.25? Per song. Write and some solve an inequality to find the most songs he can.
Answers
Answer:
Step-by-step explanation:
Step-by-step explanation:
Given that:
Worth of gift card = $50
Cost of album purchased = $10.00
Cost per song to purchase = $1.25
Number of songs to purchase = n
Inequality to model the situation :
Cost of album + cost per song * (Number of songs) ≤ worth of gift card
$10.00 + ($1.25 * n) ≤ $50
$10.00 + $1.25n ≤ $50
The body temperatures of a group of healthy adults have a bell-shaped distribution with a mean of 98.27°F and a standard
deviation of 0.54°F. Using the empirical rule, find each approximate percentage below.
a. What is the approximate percentage of healthy adults with body temperatures within 1 standard deviation of the mean, or
between 97.73 °F and 98.81°F?
Answers
Answer: follow this you'll be able to solve it
Step-by-step explanation: mean = 98.11F
standard deviation = 0.56F
99.79 – 98.11 = 1.68 = 3 standard deviations
96.43 – 98.11 = –1.68 = –3 standard deviations
96.43F and 99.79F are 3 standard deviations from the mean 98.11F.
By the empirical rule we know that 99.7% of the data lies within 3 standard deviation of the mean.
Approximately 68% of healthy adults in this group have body temperatures within 1 standard of the mean, or between 97.55F and 98.67F.
I need you to make a problem and solve it on the side and explain how explain it I’m making a practice test and I can show you examples of how I did the others This are the topics you can choose fromTopic 1: is the relation a function- domain and range Topic 2: zero is of a function

Answers
For topic (1), we have the following question:
Which of the following is a function: y=x² or x=y²?
Identify domain and range of each equation.
We can identify a given relation if it is a function or not by identifying the number of possible values of y.
The equations below are both relations.
\(y=x^2\text{ and }x=y^2\)However, only one of them is a function.
For the first equation, note that for each value of x, there is only one value of y. Some of the points on the equation are as follows.
\(\begin{gathered} x=-2 \\ y=x^2^{} \\ y=(-2)^2=4 \\ \\ x=0 \\ y=x^2 \\ y=0^2=0 \\ \\ x=2 \\ y=x^2 \\ y=2^2 \\ y=4 \end{gathered}\)Thus, the equation passes through the following points.
\((-2,4),(0,0),(2,4)\)Notice that no value of x is repeated. Therefore, the given relation is a function.
We can also determine it using graphs. The image below is the graph of the first equation.
If we test it using the vertical line test, no vertical line can pass through the graph twice. Therefore, it shows that the equation is a function.
On the otherhand, the other equation is not a function. This is because when we substitute -2 and 2 to the value of y, we will have the same value of x, which is equal to 4.
\(\begin{gathered} y=-2^{} \\ x=y^2 \\ x=(-2)^2=4 \\ \\ y=2 \\ x=y^2^{} \\ x=2^2=4 \end{gathered}\)Since there are two values of y for only one value of x, the equation must not be a function.
To illustrate this using its graph, we can notice that the vertical line below passes through two points on the graph when x=4.
Therefore, the second equation is not a function.
As for the domain and range, we can obtain it from both graphs.
The domain the set of all possible values of x. Thus, for the first equation, since it extends indefinitely to the left and right, the domain must be from negative infinity to positive infinity.
\(D_1\colon(-\infty,\infty)\)On the otherhand, since the second equation extends indefinitely to the right from 0, the domain must be from 0 to positive infinity, inclusive.
\(D_2\colon\lbrack0,\infty)\)As for the range, it is the set of all possible values of y.
Thus, for the first equation, since the graph extends indefinitely upwards from 0, the range must be from 0 to positive infinity, inclusive.
\(R_1\colon\lbrack0,\infty)\)On the otherhand, the graph of the second equation extends indefinitely upwards and downwards. Thus, its range must be from negative infinity to positive infinity.
\(R_2\colon(-\infty,\infty)\)To summarize, here are the questions and the answers for each question.
Which of the following is a function: y=x² or x=y²?
Answer: y=x²
Identify domain and range of each equation.
Answer:
For y=x²:
\(\begin{gathered} D\colon\text{ (-}\infty,\infty\text{)} \\ R\colon\lbrack0,\infty) \end{gathered}\)For x=y²:
\(\begin{gathered} D\colon\lbrack0,\infty) \\ R\colon(-\infty,\infty) \end{gathered}\)

How many two-digit, positive integers can be formed from the digits 1, 3, 5, and 9, if no digit is repeated?
24
16
12
Answers
Answer:
12
Step-by-step explanation:
Using Permutation Formula :
⁴P₂4! / 2!4 x 3 x 2! / 2!4 x 312how many ft is equal to 1.66m
Answers
Answer:
5.44 meters
Step-by-step explanation:
We Know
0.3048 meter = 1 ft
How many ft makes a height of 1.66m?
We Take
1.66 ÷ 0.3048 ≈ 5.44 meters
So, the answer is 5.44 meters.
Find the common difference of the sequence 4, 12, 20, ....
Answers
8
In this pattern, we have 4 12 then 20.
We can see that the difference 4 and 12 is 8.
Since the difference between 12 and 20 is also 8, the common difference of the sequence is 8.
What is 4a I will give brainiest to whoever’s is first

Answers
Answer:
I guess the equation would be 1s+1w+1j+4c= 6L
Step-by-step explanation:
the question is a bit confusing, but i hope this helped
ABCD is a trapezium in which AB= (3x + 2) cm, DC = (x + 3) cm and AD = (x - 1) cm.
(a) Given that the area of the trapezium is 10 cm², show that 4x²+x-25 = 0.
(b) Solve this equation and hence calculate the length of AB, giving your answer in centimetres correct to 2 significant figures.
Answers
(a) The area of a trapezium is given by the formula:
Area = (1/2) × sum of parallel sides × distance between them
Substituting the given values, we get:
10 = (1/2) × (AB + DC) × h
where h is the perpendicular distance between AB and DC.
We can express h in terms of AB and DC using the Pythagorean theorem, since AD is the height of the right triangle ACD:
AD² + h² = DC²
(x - 1)² + h² = (x + 3)²
x² - 2x + 1 + h² = x² + 6x + 9
h² = 8x + 8
Substituting this value of h² in the equation for the area, we get:
10 = (1/2) × (AB + DC) × (sqrt(8x + 8) / sqrt(1))
10 = (1/2) × (AB + DC) × sqrt(8x + 8)
Substituting the given values of AB and DC in terms of x, we get:
10 = (1/2) × ((3x + 2) + (x + 3)) × sqrt(8x + 8)
10 = (2x + 5) × sqrt(8x + 8)
(2x + 5)² × (8x + 8) = 100
(2x + 5)² × 2(x + 1) = 25
4x² + 4x + 25 = 25
4x² + x - 25 = 0
(b) We can solve the quadratic equation 4x² + x - 25 = 0 using the quadratic formula:
x = [-b ± sqrt(b² - 4ac)] / 2a
where a = 4, b = 1, and c = -25.
Substituting the values, we get:
x = [-1 ± sqrt(1² - 4(4)(-25))] / 2(4)
x = [-1 ± sqrt(401)] / 8
x = (-1 ± 20.025) / 8
x = -3.128 or x = 1.628
Since the length of a side cannot be negative, we reject the negative value of x and take x = 1.628.
Substituting this value of x in the expression for AB, we get:
AB = 3x + 2 = 3(1.628) + 2 = 7.884 ≈ 7.88 cm
Therefore, the length of AB is approximately 7.88 cm, correct to 2 significant figures.
Given the functions f(x)=7-2x and g(x)=5x-3 find g(f(-4)) find f(g(x))
Answers
Answer:
g(f(-4)) = -8
f(g(x)) = 13-10x
Step-by-step explanation:
g(f(-4)):
Plug in the equation f(x) into the variable x of g(x), we have:
\((gof)= 5(7-2x)-3\)
Plug in x = -4 and the answer is -8
f(g(x)):
Plug in the equation g(x) into the variable x of f(x), we have:
\(7-2(5x-3) = 7-10x+6 = 13-10x\)
Could someone do this ?

Answers
Answer:
A is the answer
Step-by-step explanation:
It's a larger number
I NEED HELP WITH THESE
I am pretty sure of my answers, so I just need someone to double check. Explanation is not needed because I know how to solve it, just needs to be checked. You can put one it you want.


Answers
Answer:
(b) 500 km (b) 6 secondsStep-by-step explanation:
1.The semi-major axis length is √47196900 = 6870 km. That distance from the center of the Earth means the satellite is ...
6780 -6370 = 500 . . . km
from the surface of the Earth.
The satellite is a maximum of 500 km from the Earth.
(It is a minimum of 250 km from Earth.)
__
2.The equation has a zero at t=6. When the car's velocity is zero, it is at a complete stop.
The car comes to a complete stop when time is 6 seconds.
(The car is still being accelerated, so it doesn't stay stopped.)
__
I prefer a graphing calculator for a quick solution. You can also solve this equation algebraically.
0 = 0.5t^2 -10.5t +45 . . . . t when v(t) = 0
t^2 -21t +90 = 0 . . . . . . . multiply by 2
(t -6)(t -15) = 0 . . . . . . . . factor
t = 6 or t = 15 . . . . . . . only t=6 is in the domain of the function

10)
Solve the triangle. Round decimal answers to the
nearest tenth.

Answers
The value of side length x and y in the right triangle is 5.7 and 9.4 respectively.
What is the value of x and y?The figure in the image is a right triangle.
Angle G = 59 degree
Hypotenuse = 11
Adjacent to angle G = x
Opposite to angle G = y
To solve for the missing side length x and y, we use the trigonometric ratio.
Note that:
Sine = opposite / hypotensue
Cosine = adjacent / hypotensue
Solving for x:
cos( G ) = adjacent / hypotensue
Plug in the values:
cos( 59 ) = x / 11
Cross multiply
x = cos( 59 ) × 11
x = 5.7 units
Solving for y:
sin( G ) = opposite / hypotensue
Plug in the values:
sin( 59 ) = y / 11
Cross multiply
y = sin( 59 ) × 11
y = 9.4 units
Therefore, the value of y is approximately 9.4 units.
Learn more about trigonometric ratio here: brainly.com/question/28016662
#SPJ1
Select the three equations that pass through the points (–4, –16) and (5, 2):
y + 4 = 2(x – 16)
y – 2 = 2(x – 5)
y = 2x – 8
y + 16 = 2(x + 4)
Answers
The equation of line passing through (-4, -16) and (5, 2) are y = 2x – 8, y - 2 = 2(x - 5) and y + 16 = 2(x + 4)
What is an equation?An equation is an expression that shows the relationship between two or more numbers and variables.
Equations are classified based on degree (value of highest exponents) as linear, quadratic, cubic and so on. Variables can be dependent or independent. Dependent variables depend on other variable while an independent variable do not depend.
The standard form for linear equation is:
y = mx + b
Where m is the slope and b is the y intercept
The equation of line passing through (5, 2) and (-4, -16) is:
y - 2 = [(-16-2)/(-4-5)](x - 5)
y - 2 = 2(x - 5)
y = 2x - 8
y + 16 = 2(x + 4)
Find out more on equation at: https://brainly.com/question/2972832
#SPJ1
A boat can travel 20 miles on 10 gallons of gasoline. How much gasoline will it need to go 34 miles?
Answers
Answer:
20 divided by 10 is 2 so for every 2 miles it travels it uses 1 gallon of gasoline. 20 + 14 is 34 so you divide 14 by 2 to get 7. then you add 10+7 to get 17. it will take 17 gallons of gasoline to go 34 miles
Step-by-step explanation:
In ΔKLM, l = 48 inches, ∠K=55° and ∠L=46°. Find the length of k, to the nearest inch.
Answers
Answer:
Step-by-step explanation:
(sin46)/48=(sin55)/k
k=48(sin55)/(sin46)
k=55 in