t is an exponential random variable with expected value 0.05, and b={t>0.1}.
(a) What is the conditional expected value of T given B?
E[T|B] = ________
(b) What is the conditional variance of T given B?
Var[T|B] = _________
Answers
Given, t is an exponential random variable with expected value 0.05, and b={t>0.1}.
(a) To find E[T|B], we need to use the formula:
E[T|B] = (1/P(B)) ∫t fT(t|B) dt
where P(B) is the probability of event B, fT(t|B) is the conditional density function of T given B.
Since t is an exponential random variable, its density function is fT(t) = λe^(-λt), for t ≥ 0, where λ is the rate parameter.
The expected value of T is E[T] = 1/λ. Given that the expected value of T is 0.05, we have λ = 1/0.05 = 20.
The probability of event B is P(B) = P(t > 0.1) = e^(-λt) = e^(-20*0.1) = e^(-2) ≈ 0.1353.
To find the conditional density function of T given B, we need to use Bayes' theorem:
fT(t|B) = (fB|T(B|t) * fT(t)) / fB
where fB|T(B|t) is the conditional density function of B given T, fT(t) is the density function of T, and fB is the marginal density function of B.
Since T and B are independent, we have fB|T(B|t) = fB(B) = 1/2, since the probability of B is 0.5.
Therefore, fT(t|B) = (1/2) * (20e^(-20t)) / 0.1353, for t > 0.1.
Substituting these values in the formula for E[T|B], we get:
E[T|B] = (1/0.1353) ∫t (1/2) * (20e^(-20t)) dt
= (1/0.1353) * [(t/2) * (-e^(-20t))]∣∣∣∣t=0.1∞
= 0.1325 (rounded to four decimal places).
Therefore, the conditional expected value of T given B is 0.1325.
(b) To find Var[T|B], we need to use the formula:
Var[T|B] = E[T^2|B] - [E[T|B]]^2
To find E[T^2|B], we need to use the formula:
E[T^2|B] = (1/P(B)) ∫t^2 fT(t|B) dt
Substituting the values we found earlier, we get:
E[T^2|B] = (1/0.1353) ∫t^2 (1/2) * (20e^(-20t)) dt
= (1/0.1353) * [(t^2/2) * (-e^(-20t))]∣∣∣∣t=0.1∞
= 0.01744 (rounded to five decimal places).
Substituting these values in the formula for Var[T|B], we get:
Var[T|B] = E[T^2|B] - [E[T|B]]^2
= 0.01744 - (0.1325)^2
= 0.00026875 (rounded to eight decimal places).
Therefore, the conditional variance of T given B is 0.
For more questions like variable visit the link below:
https://brainly.com/question/13100307
#SPJ11
Related Questions
Danielle is facing towards town A, which is at a bearing of 300 degrees from her. If she turns 135 degrees clockwise, she will be facing towards town B. What is the bearing of town B from Danielle?
Answers
The required bearing angle of town B from Thomas is 75°.
We have,
Bearing is basically an angle that is measured clockwise from the north. Bearing are generally written in three figure.
Given that
Thomas is facing towards town A, which is at a bearing of 300°.
Implies that town A is 300° from north.
If Thomas turns 135° clockwise, then he faces towards town B,
The bearing angle will be 300+135 = 435°
Since, one complete round makes angle 360°, therefore
The required bearing angle = 435 - 360 = 75
The bearing angle of town B from Thomas is 75°.
To know more about Bearing angle on:
brainly.com/question/10682201
#SPJ1
What is the vertical distance between (7, –12) to (7, 19)?
Answers
The vertical distance between (7, –12) and (7, 19) is 31 units.
What is a vertical line?
A vertical line is a straight line that goes straight up and down, perpendicular to the horizontal plane. In mathematics, a vertical line is one that has an undefined slope, since its slope cannot be calculated because the change in y-coordinates is zero.
Identify the two points: (7, –12) and (7, 19).
Note that both points have the same x-coordinate of 7, which means that they lie on a vertical line.
To find the vertical distance between the two points, we need to subtract their y-coordinates.
The y-coordinate of the first point is –12, and the y-coordinate of the second point is 19.
To find the difference between the two y-coordinates, we subtract the y-coordinate of the first point from the y-coordinate of the second point:
vertical distance = 19 - (-12)
The negative sign in front of 12 is because the y-coordinate of the first point is negative.
Simplify the expression by adding the two values:
vertical distance = 19 + 12
The final result is 31, which is the vertical distance between the two points.
Therefore, the vertical distance between (7, –12) and (7, 19) is 31 units. This means that if we were to draw a straight line between these two points, the line would be 31 units long if we measured it vertically.
To learn more about vertical lines from the given link:
https://brainly.com/question/30495648
#SPJ1
Answer:
D
Step-by-step explanation:
Which graph represents the function f(x) = |x| - 4?

Answers
Answer: The top graph.
Step-by-step explanation: The inflection is at x = 0, since the absolute value of x starts becoming greater as x decreases. E.g., at x = -2,
f(x) = |x| - 4
f(x) = |-2| - 4
f(x) = 2 - 4
f(x) = - 2
At x = -4
f(x) = |x| - 4
f(x) = |-4| - 4
f(x) = 4 - 4
f(x) = 0
Which of the following shows that the sum of two irrational numbers can be irrational?
A. (5+π)+(3-π)
B. √3+√5
C. (3+√5)+(3-√5)
D. (π/3)+(-π/3)
help?
Answers
Given:
The sum of irrational number in the options.
To find:
The option that shows the sum of two irrational numbers can be irrational.
Solution:
In option A,
\((5+\pi)+(3-\pi)=5+\pi+3-\pi\)
\((5+\pi)+(3-\pi)=5+3\)
\((5+\pi)+(3-\pi)=8\)
We know that 8 is a rational number. So, option A is incorrect.
In option B,
\(\sqrt{3}+\sqrt{5}\)
Here both numbers are irrational and it cannot be simplified further.
So, \(\sqrt{3}+\sqrt{5}\) is an irrational number and option B is correct.
In option C,
\((3+\sqrt{5})+(3-\sqrt{5})=3+\sqrt{5}+3-\sqrt{5}\)
\((3+\sqrt{5})+(3-\sqrt{5})=3+3\)
\((3+\sqrt{5})+(3-\sqrt{5})=6\)
We know that 6 is a rational number. So, option C is incorrect.
In option D,
\((\dfrac{\pi}{3})+(-\dfrac{\pi}{3})=\dfrac{\pi}{3}-\dfrac{\pi}{3}\)
\((\dfrac{\pi}{3})+(-\dfrac{\pi}{3})=0\)
We know that 0 is a rational number. So, option D is incorrect.
Therefore, the correct option is B.
help with my geometry please

Answers
Answer:
x = 11
z = 86
Step-by-step explanation:
8x + 6 and 10x-16 are vertical angles
Vertical angles are pairs of angles that are opposite each other and have the same vertex, or point of intersection. They are formed when two lines intersect at a point, and are always congruent, or of equal measure.
To solve this equation, we need to isolate the variable x on one side of the equation. To do this, we can start by subtracting 6 from both sides of the equation:
8x + 6 - 6 = 10x - 16 - 6
8x = 10x - 22
Now we can subtract 8x from both sides of the equation:
8x - 8x = 10x - 22 - 8x
0 = 2x - 22
To solve for x, we can add 22 to both sides of the equation:
0 + 22 = 2x - 22 + 22
22 = 2x
Finally, we can divide both sides of the equation by 2 to find the value of x: 22 / 2 = 2x / 2
x = 11
Therefore, the solution to the equation is x = 11.
Now that we have x, z is a supplementary angle to 8x + 6 (or you could do 10x - 16)
Supplementary angles are pairs of angles that add up to 180 degrees. They are formed when two lines intersect at a point, and the angles formed at the intersection are supplementary.
First plug in x, 8x + 6 = 8(11) + 6 = 88 + 6 = 94
180 - 94 = z
z = 86
A cylinder has a base diameter of 5 cm and a height of 8 cm.
The base diameter is increased by 15% and the height is decreased by 30%.
Find the percentage change in the volume of the cylinder.
Type each step of your working on a separate line.
Answers
Answer:
The new volume is 81.2% of the prior, this is true for any for any values of radius and height, as long as they are changed as stated.
Step-by-step explanation:
The volume of a cylinder is given by:
\(V = \pi*r^2*h\)
If we increase the diameter by 15%, then the radius is increased by 7.5% and the new radius is:
\(r_{new} = 1.075*r\)
If we decrease the height by 30%, then the new height is 70% of the prior and is given by:
\(h_{new} = 0.7*h\)
Applying to the volume formula we have:
\(V_{new} = pi*(r_{new})^2*h_{new}\)
\(V_{new} = \pi*(1.075*r)^2*0.7*h\\V_{new} = 1.16*0.7*\pi*r^2*h\\V_{new} = 0.812*\pi*r^2*h\\V_{new} = 0.812*V\)
The new volume is 81.2% of the prior, this is true for any for any values of radius and height, as long as they are changed as stated.
what is calculator with inverse tangent?
Answers
Calculator with inverse tangent is a calculator with four basic arithmetic operations and variety of functions such as logarithms, exponents, trigonometric functions etc.
A calculator with inverse tangent, commonly known as a scientific calculator, is a type of electronic calculator designed to perform mathematical calculations beyond basic arithmetic. In addition to the four basic arithmetic operations (addition, subtraction, multiplication, and division), it includes a variety of functions such as logarithms, exponents, trigonometric functions (sine, cosine, tangent), and their inverse functions (arcsine, arccosine, and arctangent).
The inverse tangent function, also known as arctangent, is one of the trigonometric functions that is commonly included in scientific calculators. It is used to determine the angle between the x-axis and a line drawn between the origin and a point on the graph of a function. In other words, it helps to find the angle whose tangent is a given number.
To use the inverse tangent function on a calculator, you will typically need to press the "tan^-1" or "arctan" button, followed by the number you want to find the arctangent of. The calculator will then display the angle in radians or degrees, depending on the mode it is set to.
Learn more about inverse tangent here
brainly.com/question/14998181
#SPJ4
100 POINTS! I WILL MARK BRAINLIEST. ONLY ANSWER IF YOU KNOW HOW TO DO IT. RANDOM ANSWERS WILL BE REPORTED! :)


Answers
Answer:
the cords are 4 -2
Step-by-step explanation:
Answer:
First pic (4, -2) second pic (-3, 2)
Can somebody help me with this? Please and Thank you

Answers
\(\text{Given that,}~ p(x) = x^2 +3 ~ \text{and}~ h(x) = \sqrt{x-3} \\\\(p \circ h)(x)\\\\=p(h(x))\\\\=p\left(\sqrt{x-3}\right)\\\\=\left(\sqrt{x-3} \right)^2 +3\\\\=x-3 +3\\\\=x\)
A model boat i 15 inche long if the boat i bulit to a cale of 1 : 250 inche how long i the real boat
define a variable
write a porortion
olve the porportion
anwer with word
Answers
If the scale of drawing is 1 inches : 250 inche and the real horse height is 15 inche, then the height of the horse in drawing is 0.06 inches.
What does a scale look like in math?The ratio that describes the relationship between the true figure itself and model is called the scale. It serves as a representation of the real statistics in smaller units on maps. A scale of 1:5, for instance, indicates that 1 on the map is approximately the size of 5 in the actual world.
Briefing:The scale of drawing the horse = 1 inch :
Therefore in scale
Horse height in drawing equals one inch
The height of the horse = 250 inche
The original height of the horse = 15 inche
The height in the picture = x inches
To find the height the horse in the picture, we have to use proportion
1 inch : 250 inche = x inches : 15 inche
1 / 250 = x / 15
1 × 15= 250x
250x = 15
x = 15/250
x = 0.06 inches
Therefore, the height of the horse in drawing is 0.06 inches
To know more about scale visit:
https://brainly.com/question/4261493
#SPJ4
What is the value of the expression x  exponent 2 when x = 4/5
Answers
Сильные слабые стороны человека
Answers
Answer:
Сильные:
Упорный, нацеленый на результат
Уверен в себе
Трудолюбивый
Общительный
Организованный
Самостоятельный
Дисциплинированный
Слабые:
Излишне стеснительный
Чрезмерно эмоциональный
Раздражительный и даже агрессивный
Не обладающий силой воли
Не умеющий вовремя промолчать
Гиперактивный
Принципиальный
(This exercise is from Physical Geology by Steven Earle and is used under a CC BY 4.0 license.) Heavy runoff can lead to flooding in streams and low-lying areas. The graph below shows the highest discharge per year between 1915 and 2014 on the Bow River at Calgary, Canada. Using this data set, we can calculate the recurrence interval (R) for any particular flood magnitude with the equation R=(n+1)/r, where n is the number of floods in the record being considered, and r is the rank of the particular flood. There are a few years missing in this record, and the actual number of data points is 95. The largest flood recorded on the Bow River over that period was in 2013, which attained a discharge of 1,840 m3/s on June 21. R; for that flood is (95+1)/1=96 years. The probability of such a flood in any future year is 1/R; which is 1%. The fifth largest flood was just a few years earlier in 2005 , at 791 m3/5. Ri for that flood is (95+1)/5=19.2 years. The recurrence probability is 5%. - Calculate the recurrence interval for the second largest flood (1.520 m3/s in 1932). Express your answer in units of years. - What is the probability that a flood of 1,520 m3/s will happen next year? - Examine the 100-year trend for floods on the Bow River. If you ignore the major floods (the labeled ones), what is the general trend of peak discharges over that time?
Answers
The recurrence interval for the second largest flood on the Bow River in 1932 is approximately 1.0106 years. The probability of a flood with a discharge of 1,520 m3/s occurring next year is roughly 98.95%. When examining the 100-year trend of peak discharges, excluding major floods, there is likely a general pattern of fluctuations but with overall stability in typical peak discharge values.
Using the provided data on the highest discharge per year on the Bow River at Calgary, Canada, we can calculate the recurrence interval (R) for specific flood magnitudes and determine the probability of such floods occurring in the future. Additionally, we can examine the 100-year trend for floods on the Bow River, excluding major floods, to identify the general trend of peak discharges over time.
1) Calculating the Recurrence Interval for the Second Largest Flood (1,520 m3/s in 1932):
To calculate the recurrence interval (R) for the second largest flood, we need to determine the rank of that flood. Since there are 95 data points in total, the rank of the second largest flood would be 94 (as the largest flood, in 2013, is excluded). Applying the formula R = (n + 1) / r, we have:
R = (95 + 1) / 94 = 1.0106 years
Therefore, the recurrence interval for the second largest flood (1,520 m3/s in 1932) is approximately 1.0106 years.
2) Probability of a Flood of 1,520 m3/s Occurring Next Year:
The probability of a flood of 1,520 m3/s happening next year can be calculated by taking the reciprocal of the recurrence interval for that flood. Using the previously calculated recurrence interval of 1.0106 years, we can determine the probability:
Probability = 1 / R = 1 / 1.0106 = 0.9895 or 98.95%
Thus, the probability of a flood of 1,520 m3/s occurring next year is approximately 98.95%.
3) Examination of the 100-Year Trend for Floods on the Bow River:
To analyze the 100-year trend for floods on the Bow River while excluding major floods, we focus on the peak discharges over time. Without considering the labeled major floods, we can observe the general trend of peak discharges.
Unfortunately, without specific data on the peak discharges for each year, we cannot provide a detailed analysis of the 100-year trend. However, by excluding major floods, it is likely that the general trend of peak discharges over time would show fluctuations and variations but with a relatively stable pattern. This implies that while individual flood events may vary, there might be an underlying consistency in terms of typical peak discharges over the 100-year period.
In summary, the recurrence interval for the second largest flood on the Bow River in 1932 is approximately 1.0106 years. The probability of a flood with a discharge of 1,520 m3/s occurring next year is roughly 98.95%. When examining the 100-year trend of peak discharges, excluding major floods, there is likely a general pattern of fluctuations but with overall stability in typical peak discharge values.
Learn more about probability here
https://brainly.com/question/25839839
#SPJ11
triangle ABC is a right triangle whose right angle is
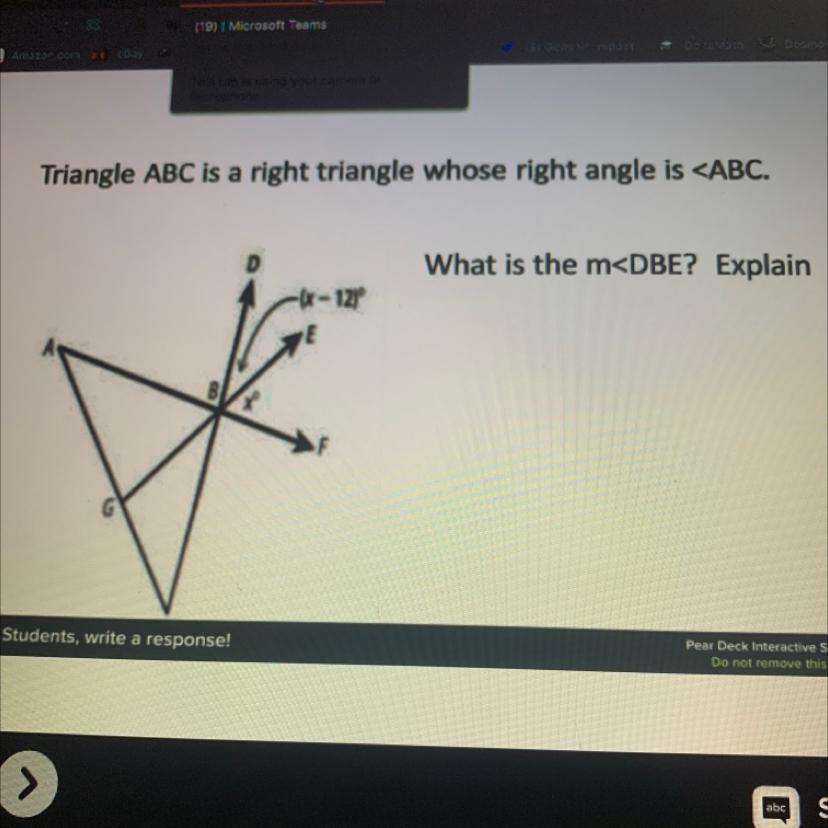
Answers
If triangle ABC is a right triangle and
A half circle has 180 degrees, so the sum of \(\begin{gathered} 90\text{ + (}x\text{-12)}+x\text{ = 180 } \\ x\text{ - 12 + x = 180 - 90 } \\ 2x\text{ - 12 = 90} \\ 2x\text{ = 90 + 12} \\ 2x\text{ = 102} \\ x=\text{ 102/2 } \\ x=\text{ 51º} \end{gathered}\)So, if x= 51º, then m


Find the range of the function y=3-x when the domain is {-2, 0, 3}
Answers
Answer:
-3
Step-by-step explanation:
when u look at it or slove it
Answer:
Step-by-step explanation:
The range is going to be the y value in this case.
y = 3 - - 2
y = 5
y = 3 - 0
y = 3
y = 3 - 3
y = 0
(5,3,0)
When you subtract an number from both sides of an inequality, do you flip or change the direction of the inequality?
Answers
Answer:
you only have to flip the inequality if you you are divide or multiplying by a negative
Helpppp need now!! Please thanks you

Answers
Answer:
The last one is incorrect
Step-by-step explanation:
Sam drove from San Diego (elevation 210 feet) to the Grand Canyon (elevation -247 feet). What is the difference in elevation between San Diego and the Grand Canyon?
Answers
Answer:
The difference is elevation is 457 feet.
Step-by-step explanation:
You simply add the two numbers together.
The equation y = 0.75 represents the cost of watermelon in dollars (y) and the number of Pounds of watermelon(x). What is the cost of an 11 pound watermelon?
Answers
The cost of 11 pounds of watermelon is $8.25.
What is an equation?
There are many different ways to define an equation. The definition of an equation in algebra is a mathematical statement that demonstrates the equality of two mathematical expressions. For instance, the equation 4x + 8 = 17 consists of the two expressions 4x + 8 and 17, which are separated by the 'equal' sign. Mathematical algebraic equations typically have one or more variables.
The given equation is y = 0.75x, where x represents the number of Pounds of watermelon and y represents the cost of watermelon in dollars.
Putting x = 11 in the equation y = 0.75x:
y = 0.75×11
y = 8.25
The cost of 11-pound watermelon is $8.25.
To learn more about the substitution in an equation, click on the below link:
https://brainly.com/question/5433795
#SPJ1
What is the LCD of 8 5/12 and 3 5/8?
A.24
B.96
D.48
C.16
Answers
Answer:
24
Step-by-step explanation:
12, 24
8, 16, 24
Given that triangle RST is isosceles, find the value of ZS

Answers
Answer:
120°
Step-by-step explanation:
\(m\angle S = 180\degree - 2\times 30\degree \\\\
m\angle S = 180\degree - 60\degree \\\\
\huge\purple {\boxed{m\angle S = 120\degree}} \)
The economy is in a recession. Real GDP is well below potential GDP. If the government wants to increase real GDP so that it is closer to potential GDP, it could ____. (Select all that apply.) Group of answer choices -increase government spending -decrease government spending -decrease taxes -increase taxes
Answers
To increase real GDP and bring it closer to potential GDP during a recession, the government could increase government spending and/or decrease taxes.
During a recession, when real GDP is below potential GDP, the government can use fiscal policy tools to stimulate economic growth and close the GDP gap. The two options that can be effective in this situation are increasing government spending and decreasing taxes.
Increase government spending: By increasing spending on infrastructure projects, education, healthcare, or other sectors, the government can create demand in the economy, which leads to increased production and employment, ultimately raising real GDP.
Decrease taxes: Reducing taxes can provide individuals and businesses with more disposable income, encouraging consumption and investment. This increased spending and investment can boost aggregate demand, leading to higher production levels and closing the GDP gap.
Decreasing government spending and increasing taxes, on the other hand, would have contractionary effects, potentially exacerbating the recessionary conditions by reducing overall demand in the economy. Therefore, these options are not suitable for increasing real GDP during a recession.
Learn more about GDP here: brainly.com/question/32551875
#SPJ11
Your total for dinner was $18.50. If you want to leave a 20% tip, how much will your grand total be?
Answers
Answer:
$3.70 honestly just divide lol
what can sometimes be a rhombus
A. parallelogram
B. rectangle
C. quadrilateral
D. trapezoid
Answers
Answer:
A, parallelogram
Step-by-step explanation:
Because they are both parallel.
Answer:
I am not shure, but I think it is C.
Hey um can somone help me out please i dont know what is correct and wrong

Answers
2. Calculator Boy is correct, while Mathy Girl is wrong. After Calculator Boy distributed the 2, he correctly calculated that the 8x could not be subtracted by the “-6 -7”. It left his equation with “8x -13” as the -6 and -7 would combine. Mathy Girl distributed correctly as well, however, she wrote that you could subtract the “-6” from the “8x” which cannot happen. The -6 does not have a variable (x), so it cannot subtract from the “8x”.
I apologize if the explanation is a bit confusing… comment if you would like extra help and I can try to explain it differently!
An auditing software can identify 63.7% of misreporting issues in accounting ledgers. Let X be the number of accounting misreporting transactions identified by the software among 50 randomly selected transactions for the last 3 months.
Determine the probability that no misreported transactions are found.
Determine the probability that less than 10 misreported transactions are found.
Determine the probability that at least half of the transactions are misreported.
If the firm applying the auditing software as a test run finds no misreporting, it will receive a $200 compensation, but if there are less than 10 misreported transactions it will have to pay a fee of $50, and if the misreported transactions represent more than half of the transactions then the fee will be $100. Determine the expected monetary gain (assuming that the auditing software is correct when identifying a misreporting).
Answers
The auditing software can identify 63.7% of misreporting issues in accounting ledgers. The probability that no misreported transactions are found is 1 - 63.7% = 36.3%. The probability that at least half of the transactions are misreported is 1 - P(X 25) = 1 - P(X 24) P(X 24) = _(i=0)24 (50C_i) (0.363)i (1 - 0.363)(50 - i) 0.0001. The expected monetary gain is approximately -$49.8.
Given that an auditing software can identify 63.7% of misreporting issues in accounting ledgers. Let X be the number of accounting misreporting transactions identified by the software among 50 randomly selected transactions for the last 3 months.Probability that no misreported transactions are found:X follows a binomial distribution with n = 50 and p = 1 - 63.7% = 36.3%.P(X = 0) = (1 - p)^n = (1 - 0.637)^50 ≈ 0.0002Probability that less than 10 misreported transactions are found:
P(X < 10) = P(X ≤ 9)P(X ≤ 9)
= P(X = 0) + P(X = 1) + P(X = 2) + ... + P(X = 9)P(X ≤ 9)
= ∑_(i=0)^9 (50C_i ) (0.363)^i (1 - 0.363)^(50 - i) ≈ 0.99
Probability that at least half of the transactions are misreported:
P(X ≥ 25)P(X ≥ 25)
= P(X > 24)P(X > 24)
= 1 - P(X ≤ 24)P(X ≤ 24)
= ∑_(i=0)^24 (50C_i ) (0.363)^i (1 - 0.363)^(50 - i) ≈ 0.0001
Expected monetary gain:Let Y be the amount of money that the firm gets to earn or pay. The probability distribution of Y can be shown below:Outcomes: $200, -$50, -$100
Probabilities: P(X = 0), P(0 < X < 10), P(X ≥ 25)P(X = 0)
= 0.0002P(0 < X < 10)
= 0.99 - 0.0002 = 0.9898P(X ≥ 25)
= 0.0001E(Y)
= ($200 x P(X = 0)) + (-$50 x P(0 < X < 10)) + (-$100 x P(X ≥ 25))E(Y)
= ($200 x 0.0002) + (-$50 x 0.9898) + (-$100 x 0.0001)≈ -$49.8
Therefore, the expected monetary gain is approximately -$49.8.
To know more about probability Visit:
https://brainly.com/question/31828911
#SPJ11
find each missing length to the nearest tenth

Answers
Answer: 4.1
Step-by-step explanation: To find a missing leg you must square both numbers, then subtract the leg you do have from the hypotenuse ( 33.64 - 16.81) to get the squared number for the missing leg ( 16.83). You then have to find the square root of that number and round to the nearest tenth (4.1).
ch02 04 given wins = a0 a1 x population e1 . what is the regression term that describes a0 in the equation?
Answers
a0 is the regression term that describes the constant or intercept in the linear regression equation.
In a simple linear regression model, the equation takes the form of y = a0 + a1x + e1, where y is the dependent variable (or response variable), x is the independent variable (or predictor variable), a0 is the intercept or constant term, a1 is the coefficient of the independent variable, and e1 is the error term.
The intercept term, a0, represents the value of the dependent variable when the independent variable is zero. For example, in a linear regression model that predicts salary based on years of experience, the intercept would represent the starting salary for someone with zero years of experience. The intercept is an important component of the regression equation because it allows us to make predictions for values of x that are outside the range of our observed data.
The coefficient, a1, represents the change in the dependent variable for each one-unit increase in the independent variable. In the salary example, the coefficient would represent the average increase in salary for each additional year of experience.
Both the intercept and coefficient are estimated from the data using methods such as least squares regression. Once these values are estimated, we can use them to make predictions for new values of x.
Learn more about equation from
https://brainly.com/question/29174899
#SPJ11
Please help me solve this.

Answers
Step-by-step explanation:
Steps are in the picture above.
Note:if you need to ask any question please let me know.

a nurse manager approves two staff nurses to attend a national conference
Answers
The nurse manager approves two staff nurses to attend a national conference.
The nurse manager has given their authorization or consent for two staff nurses to participate in and attend a national conference. This decision indicates that the nurse manager recognizes the value and relevance of the conference for professional development and sees the benefit of the staff nurses' participation. By approving their attendance, the nurse manager demonstrates support for their growth, learning, and exposure to new knowledge, experiences, and networking opportunities available at the conference.
To know more about nurse,
https://brainly.com/question/29544576
#SPJ11