Suppose you work as ski instructor over winter break earning $12 per hour. The amount of your weekly paycheck (before taxes are taken out) could be written F(x) = 12x.
Answers
Answer: Yes.
Step-by-step explanation:
Yes, that is correct. The variable x represents the hours you worked each week.
Related Questions
Find the specified areas for a Upper N left-parenthesis 0 comma 1 right-parenthesis density. (a) The area below z equals 1.04 Round your answer to three decimal places. areaequals the absolute tolerance is +/-0.001 (b) The area above z equals -1.4 Round your answer to three decimal places. areaequals the absolute tolerance is +/-0.001 (c) The area between z equals 1.1 and z equals 2.1 Round your answer to three decimal places. areaequals the absolute tolerance is +/-0.001
Answers
The area between z=1.1 and z=2.1 is approximately 0.982 - 0.864 = 0.118, rounded to three decimal places.
To find the area below z=1.04 for an Upper N(0,1) density, you will need to use the standard normal distribution table or a calculator with a z-table function. Here are the steps:
1. Locate the value of z=1.04 in the table or use the calculator's function.
2. Find the corresponding area value (which represents the probability or percentage of values below z=1.04).
The area below z=1.04 is approximately 0.851, rounded to three decimal places.
(b) To find the area above z=-1.4 for an Upper N(0,1) density, follow these steps:
1. Locate the value of z=-1.4 in the table or use the calculator's function.
2. Find the corresponding area value.
3. Since we need the area above z=-1.4, subtract the area value found in step 2 from 1.
The area above z=-1.4 is approximately 1 - 0.0808 = 0.919, rounded to three decimal places.
(c) To find the area between z=1.1 and z=2.1 for an Upper N(0,1) density, follow these steps:
1. Locate the values of z=1.1 and z=2.1 in the table or use the calculator's function.
2. Find the corresponding area values for both z=1.1 and z=2.1.
3. Subtract the area value of z=1.1 from the area value of z=2.1 to find the area between them.
The area between z=1.1 and z=2.1 is approximately 0.982 - 0.864 = 0.118, rounded to three decimal places.
Learn more about area
brainly.com/question/27683633
#SPJ11
Help meee please help meeee
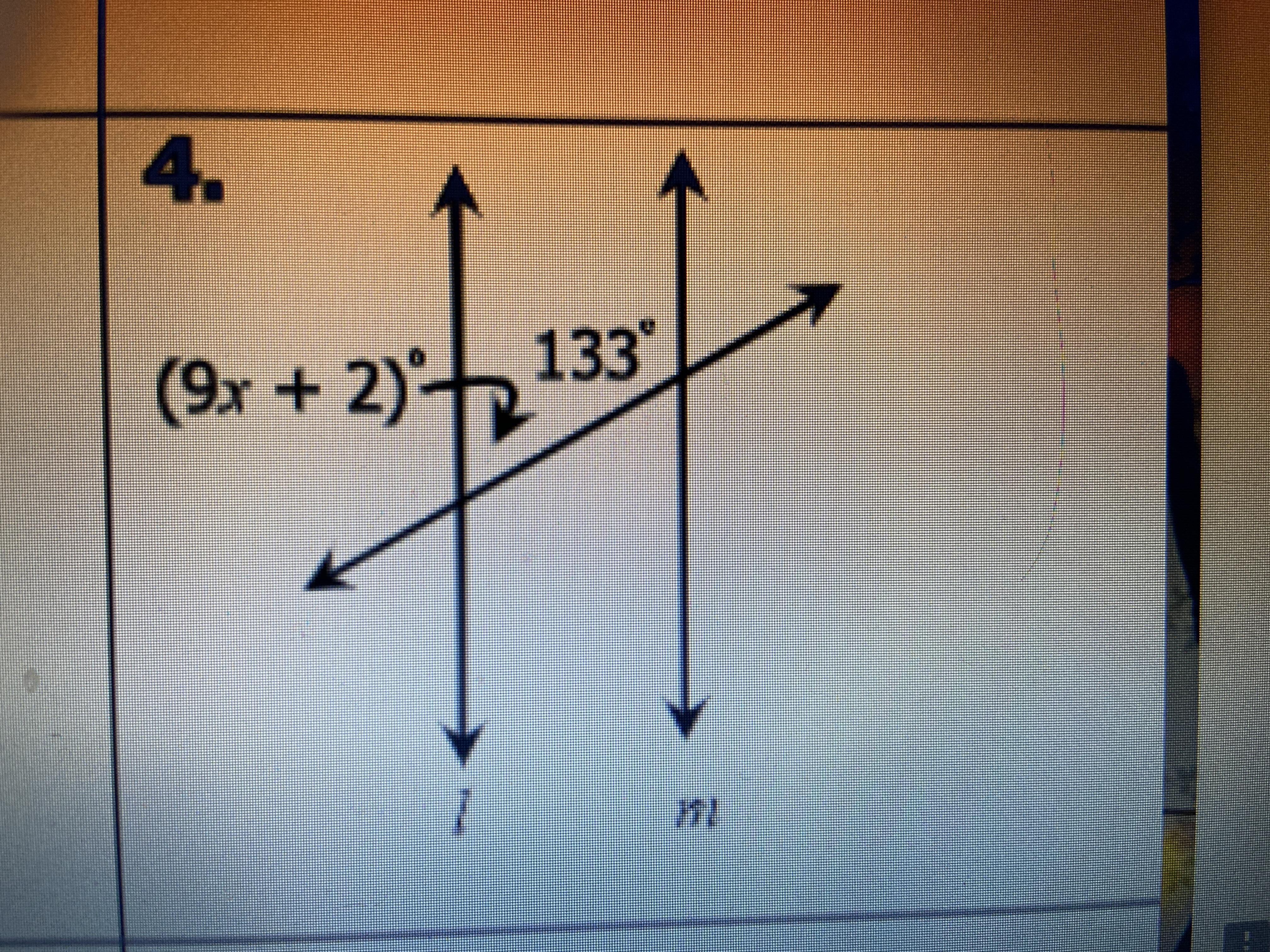
Answers
Answer:
133+9x+2=180 (sum of interior angle on the same side of transversal is 180°)
9x=180-135
x=5
U can either subtract 2 and 133 from both sides or subtract 135 (133+2)
Which gives you:
9x= 45
The u divide 9 on both sides to get x alone
Which leaves with:
X=5 which is ur answer
(5.) Verify the first four Euclidean postulates in single elliptic geometry. Hint: Imitate the corresponding proofs of these results in hyperbolic geometry. (See Chapter 7.)
Answers
In elliptic geometry, which is a non-Euclidean geometry, the first four Euclidean postulates are not valid.
However, we can still examine how they are violated and discuss the corresponding proofs in hyperbolic geometry.
1. First Postulate (Postulate of Line Existence):
Euclidean Postulate:
Given any two distinct points, there exists a unique line that passes through them.
Violation in Elliptic Geometry:
In elliptic geometry, any two distinct points do not have a unique line passing through them.
Instead, there are multiple lines that pass through any two points.
Proof in Hyperbolic Geometry:
In hyperbolic geometry, we can prove that given any two distinct points, there are infinitely many lines passing through them.
This can be demonstrated using the Poincaré disk model or the hyperboloid model.
2. Second Postulate (Postulate of Line Extension):
Euclidean Postulate:
Any line segment can be extended indefinitely to form a line.
Violation in Elliptic Geometry:
In elliptic geometry, a line segment cannot be extended indefinitely since the lines in this geometry are closed curves.
Proof in Hyperbolic Geometry:
In hyperbolic geometry, we can show that a line segment can be extended indefinitely by demonstrating the existence of parallel lines that do not intersect.
3. Third Postulate (Postulate of Angle Measure):
Euclidean Postulate:
Given a line and a point not on the line, there exists a unique line parallel to the given line.
Violation in Elliptic Geometry:
In elliptic geometry, there are no parallel lines.
Any two lines will eventually intersect.
Proof in Hyperbolic Geometry:
In hyperbolic geometry, we can prove the existence of multiple parallel lines through a given point not on a line.
This can be achieved by showing that the sum of angles in a triangle is always less than 180 degrees.
4. Fourth Postulate (Postulate of Congruent Triangles):
Euclidean Postulate:
If two triangles have three congruent sides, they are congruent.
Violation in Elliptic Geometry:
In elliptic geometry, two triangles with three congruent sides may not be congruent.
Additional conditions, such as congruent angles, are necessary to determine triangle congruence.
Proof in Hyperbolic Geometry:
In hyperbolic geometry, we can prove that two triangles with three congruent sides are congruent.
This can be demonstrated using the hyperbolic version of the SAS (Side-Angle-Side) congruence criterion.
In summary, in elliptic geometry, the first four Euclidean postulates are not valid, and their corresponding proofs in hyperbolic geometry show how these postulates are violated or modified to fit the geometrical properties of the respective geometries.
Lean more about Euclidean postulates from this link:
https://brainly.com/question/28165056
#SPJ11
An object is moving at a speed of 2 centimeters ever 7 seconds. express this speed in meters per week.
Answers
The speed of the object is 12121 m per week.
What does it mean to do speed?
“Speed” is a street name for various stimulant drugs that teens, young adults and others use to feel more alert and focused, and in some cases, to feel high. Some people also use various forms of speed to reduce their appetite. Types of speed include: Amphetamines (used to treat ADHD, narcolepsy, and depression)The object is moving at a speed of 2 centimeters every 7 seconds.
We need to find the speed in m per week.
2 cm = 0.02 m
1 week = 604800 s
7 s = \(1.65 * 10^{-6} week\)
Speed = distance/time
So,
\(v = \frac{0.02 m}{1.65 * 10^{-6 } week}\)
\(v = 12121.21 m/ week\)
or v = 12121 m/ week
So, the speed of the object is 12121 m per week.
Learn more about speed
brainly.com/question/7359669
#SPJ4
Compute the limit by substituting the Maclaurin series for the trig and inverse trig functions. (Use symbolic notation and fractions where needed.) tan(9x) – 9x cos (9x) – 243 x3 — = lim x0 75
Answers
The limit is -243/75 or -3.24.
How did we get the value?To compute the limit using the Maclaurin series for trigonometric and inverse trigonometric functions, express each term in the given expression using their respective series expansions. Break down each term:
1. The Maclaurin series expansion for tangent (tan) function is:
tan(x) = x + (x³)/3 + (2x⁵)/15 + (17x⁷)/315 + ...
Substitute 9x for x in this series expansion to get the Maclaurin series for tan(9x):
tan(9x) = 9x + (81x³)/3 + (2 x (729x⁵))/15 + (17 × (6561x⁷))/315 + ...
2. The Maclaurin series expansion for cosine (cos) function is:
cos(x) = 1 - (x²)/2 + (x⁴)/24 - (x⁶)/720 + ...
Again, substitute 9x for x in this series expansion to get the Maclaurin series for cos(9x):
cos(9x) = 1 - (81x²)/2 + (6561x⁴)/24 - (59049x⁶)/720 + ...
3. The cubic term, 243x³, does not require substitution or approximation.
Now, rewrite the given expression using the Maclaurin series for trigonometric and inverse trigonometric functions:
lim(x->0) [tan(9x) - 9x cos(9x) - 243x³]/75
= lim(x->0) [(9x + (81x³)/3 + (2 × (729x⁵))/15 + (17 × (6561x⁷))/315) - 9x(1 - (81x²)/2 + (6561x⁴)/24 - (59049x⁶)/720) - 243x³]/75
Now, simplify and collect the terms with the same power of x:
= lim(x->0) [(9x - 9x) + (81x³/3 - 81x³/2) + (2 × (729x⁵)/15) - (17 × (6561x⁷)/315) + (9x³/2) - (81x⁵/24) + (729x⁷/80) - (17 × (6561x⁷)/315) - 243x³]/75
The terms (9x - 9x) and (81x³/3 - 81x³/2) cancel out, leaving:
= lim(x->0) [(2 × (729x⁵)/15) - (17 × (6561x⁷)/315) + (9x³/2) - (81x⁵/24) + (729x⁷/80) - (17 × (6561x⁷)/315) - 243x³]/75
Now, simplify further and remove the common factor of x³ from the remaining terms:
= lim(x->0) [(2 × (729x²)/15) - (17 x (6561x⁴/315) + (9x/2) - (81x²/24) + (729x⁴80) - (17 x. (6561x⁴)/315) - 243]/75
Finally, take the limit as x
approaches 0 by directly substituting x = 0 into the expression:
= [(2 × (729(0)²)/15) - (17 x (6561(0)⁴)/315) + (9(0)/2) - (81(0)²/24) + (729(0)⁴/80) - (17 × (6561(0)⁴)/315) - 243]/75
= [-243]/75
Simplifying further:
= -243/75
Therefore, the limit is -243/75 or -3.24.
learn more about trigonometric functions: https://brainly.com/question/25618616
#SPJ4
Please Help! No Silly Answers Please! I would appreciate correct answers. Thank you all! Please try and include Scratch Work, Thank you.

Answers
Answer:
y in (7,y) = 14
Step-by-step explanation:
A General Linear function is as the following:
y = mx + c, Where: m: slope of the line, c: y-intercept
Given that:
Point 1 (P1) = (1,5)
Point 2 (P2) = (3, 11)
Point 3 (P3) = (7,y)
By substituting in the linear function with P1:
5 = m + c ---> (1)
By substituting in the linear function with P2:
11 = 3m + c ---> (2)
By multiplying equation (1) times 3 and subtracting eq. (2) from it:
(15 = 3m + 3c) - (11 = 3m + c) =
4 = 2c
Then, c = 2
By substituting with "c" in eq. (1):
5 = m + 2
Then, m = 3
Hence,
the function of this line is:
y = 3x + 2
So,
to get "y" in P3, we are going to substitute with 7:
y = 3(7) + 2
then "y" in P3 = 23
Another Solution:
by getting the slope of the line:
\(Slope = \frac{\triangle y}{\triangle x}\) Where: Δy: change in y points, Δx: change in x points
by utilizing P1 & P2 in slope formula:
\(slope = \frac{11 - 5}{3 - 1} = \frac{6}{2} = 3\)
By substituting with P1 in the linear function:
5 = 3 + c
Then, c = 2
the function of the line is:
y = 3x + 2
So,
to get "y" in P3, we are going to substitute with 7:
y = 3(7) + 2
then "y" in P3 = 23
hope you find this easy to understand....
Have any questions? Write in the comments.
give me brainliest if you found this answer useful
HELP PLSSSSS TY
Health Club Fees You are choosing between two health clubs. Club A offers membership for a fee of $14 plus a monthly fee of $29. Club B offers membership for a fee of $28 plus a monthly fee of $22. After how many months will the total cost of each health club be the same?
Answers
Answer:
2 months
Step-by-step explanation:
To solve this equation create an expression for the cost of each club. Use the slope-intercept form of y=mx+b where m is the monthly fee and b is the flat fee. So the 2 expressions would be A) 29x+14 and B) 22x+28. Since we want to find when these are equal, set the expressions equal to each other. This gives the equation 29x+14=22x+28. Then, solve for x.
29x+14=22x+287x+14=287x=14x=2When solved, x=2. This means that after 2 months the cost of each will be the same.
A group of 4 people go to a restaurant and the bill without tax comes to $105.73. Tax is 6%. Remember to round to the nearest hundredth because this is money. After tax is added, you want to leave a 20% tip on the new total. The group of 4 people decides to split the total cost equally. How much will each person pay?
i need the answer fasttttt
Answers
Each person need to pay $ 80.88345.
What is Unitary Method?The unitary technique involves first determining the value of a single unit, followed by the value of the necessary number of units.
For example, Let's say Ram spends 36 Rs. for a dozen (12) bananas.
12 bananas will set you back 36 Rs. 1 banana costs 36 x 12 = 3 Rupees.
As a result, one banana costs three rupees. Let's say we need to calculate the price of 15 bananas.
This may be done as follows: 15 bananas cost 3 rupees each; 15 units cost 45 rupees.
Given:
Bill without tax = 105.73
Tax = 6%
So, bill amount after tax = 105. 73 + 105. 73 x 6/100
= 105.73 + 6.3438
= $112.0738
Addition of 20% tip = 112.0738 + 211.46 = $323.5338.
If the amount is divided among 4 people, each will pay
= 323.5338/4
= $ 80.88345
Learn more about Unitary Method here:
https://brainly.com/question/22056199
#SPJ1
a rose garden is formed by joining a rectangle and a semicircle, as shown below. the rectangle is long and wide. if the gardener wants to build a fence around the garden, how many feet of fence are required? (use the value for , and do not round your answer. be sure to include the correct unit in your answer.)
Answers
A rose garden is formed by rectangular and semi-circular parts. If the gardener wants to build a fence around the garden, then total 134.95 feet of fence are required.
The perimeter is defined as calculating the outer length of boundaries of shape.
Perimeter of semi-circle : The product of pi and the radius of a semi-circle is known as the perimeter of the semi-circle, P = π× radius. The sum of the length of the four sides of a rectangle is known as the perimeter of a rectangle, P = 2( length + width).We have a rose garden is formed by joining a rectangle and a semicircle, as present in above figure. We have to determine the feet of fence are required to build a fence around the garden.
From the above figure, length of rectangular part, l = 34 ft
Width of rectangular part, w = 26 ft.
Also, diameter of semi-circular part, d
= 26 ft
Radius of of semi-circular part, r = d/2
= 26/2 ft = 13 ft
So, the perimeter of semi-circular part, Pₛ= π× r = π× 13 ft
= 40.95 ft.
Here, the fence required for the rectangle shape is three sides that two long sides and one wide side. The fourth side of the width is already covered by the semi-circular part. So, the perimeter formula for the rectangle shape, Pᵣ = 2l + w. Therefore, perimeter of garden
= Pₛ + Pᵣ
= 40.95 ft + 2×34 ft + 26 ft
= 68 ft + 26 ft + 40.95 ft
= 134.95 ft.
Hence, required value is 134.95 feet.
For more information about perimeter, refer:
https://brainly.com/question/19819849
#SPJ4
Complete question:
The above figure complete the question. a rose garden is formed by joining a rectangle and a semicircle, as shown below. the rectangle is 34 feet long and 26 feet wide. if the gardener wants to build a fence around the garden, how many feet of fence are required? (use the value for , and do not round your answer. be sure to include the correct unit in your answer.)

The sphere has a radius of 12 meters, What is the volume of the sphere
Answers
\(\Large{\underline{\mathcal{Given: }}}\)
radius = 12m
volume = ❓
\(\Large{\underline{\mathcal{solution :}}}\)
volume of a sphere:
☞4/3 πr³ cu.units
☞4/3 × 22/7 × 12 × 12 × 12
☞ 7214 m³
0.1 6
---- =. -----
0.4. P
With solution please
Answers
Answer:
I think it is 0.12P because 16-4 is 12 so yeah. that is what I think
Order these numbers from least to greatest.
3/4, -1/5, -5/16, 0.90, -0.52
0.90, 3/4, -5/16 , -0.52, -1/5
-1/5 , -5/16 , -0.52, 3/4, 0.90
0.90, 3/4, -0.52, -5/16 , -1/5
-0.52, -5/16 , -1/5 , 3/4, 0.90
Answers
Answer:
0.90, 3/4, -5/16 , -0.52, -1/5Step-by-step explanation:
A charity organization is having a fundraiser. P represents the fundraiser's profit (in dollars) if n tickets are sold. A negative profit means the expenses exceeded the income from tickets. P=70n-1500. What are the expenses of the fundraiser?
Answers
P = 70n - 1500
If the profit P is negative, then the expenses of the fundraiser exceeded the income from tickets.
Setting P equal to zero and solving for n gives us the breakeven point, which is the number of tickets that must be sold to cover the expenses:
0 = 70n - 1500
70n = 1500
n = 21.43
Since we can't sell a fractional number of tickets, we will round up to the nearest whole number, which gives us:
n = 22
Therefore, if the organization sells 22 tickets, the profit will be zero, and the expenses will be equal to the revenue generated by the ticket sales:
P = 70n - 1500
P = 70(22) - 1500
P = 1540 - 1500
P = 40
So the expenses of the fundraiser would be $40 if they sell 22 tickets.
Find the surface area of the triangular prism shown below.
12
units²
10
10
14.
Answers
Answer:
The triangular prism has two triangular bases and three rectangular lateral faces.
First, we need to find the area of each triangular base. Using the formula for the area of a triangle:
base x height / 2
We can calculate the area of one triangular base as:
(10 x 12) / 2 = 60 units²
Now we need to find the area of each rectangular lateral face. All three faces have the same dimensions of 10 units by 14 units, so the area of each face is:
10 x 14 = 140 units²
To find the total surface area of the prism, we add up the areas of both triangular bases and all three rectangular faces:
Total surface area = 2 x (area of triangular base) + 3 x (area of rectangular face)
Total surface area = 2 x 60 units² + 3 x 140 units²
Total surface area = 120 units² + 420 units²
Total surface area = 540 units²
Therefore, the surface area of the triangular prism is 540 square units.
Help!!! (Look at the picture)

Answers
Answer:
x > 90
Step-by-step explanation:
To solve this, we will use the multiplication property of equality. We need to multiply both sides by 6, this will get us x > 90.
Write the given expression as the sum and/or difference of
logarithms. Express all exponents as coefficients.
log3 (x^10z^5) =
Answers
The expression log3(x^10z^5) can be written as the sum of two logarithms: 10log3(x) + 5log3(z).
To express the given expression as the sum and/or difference of logarithms, we use the logarithmic property log_a(b^c) = clog_a(b). In this case, we have log3(x^10z^5). By applying the property, we can separate the exponents as coefficients of the logarithms. The exponent 10 in x^10 becomes the coefficient in front of the logarithm log3(x), and the exponent 5 in z^5 becomes the coefficient in front of the logarithm log3(z).
Therefore, the expression log3(x^10z^5) can be written as the sum of two logarithms: 10log3(x) + 5log3(z). This notation represents the same value as the original expression but is written in a different form that separates the variables x and z with their respective exponents as coefficients.
Learn more about logarithms here: brainly.com/question/30226560
#SPJ11
6/7 divided by 3 =
Answer please (work it out or not idc)
Answers
Answer:
Step-by-step
2/7
How do I find the slope of the image below??!!

Answers
Answer:
Step-by-step explanation:
what impact does multicollinearity have on the p-values on the slopes in a regression model?
Answers
It is important to check for multicollinearity in a regression model and take steps to reduce it, such as removing one of the highly correlated independent variables or using regularization techniques.
Multicollinearity is a statistical phenomenon where two or more independent variables in a regression model are highly correlated with each other. This can cause problems in the regression model as it becomes difficult to distinguish the individual effects of the independent variables on the dependent variable.
When multicollinearity is present in a regression model, the p-values of the slopes of the independent variables are affected. The p-value measures the probability of obtaining a result as extreme or more extreme than the observed result, assuming that the null hypothesis is true. The null hypothesis in a regression model is that the slope of the independent variable is zero, meaning that there is no relationship between the independent variable and the dependent variable.
Multicollinearity can cause the standard errors of the slopes to increase, leading to inflated p-values. In other words, the significance of the relationship between the independent variable and the dependent variable may be underestimated. This is because the highly correlated independent variables are both trying to explain the same variation in the dependent variable, leading to an unreliable estimate of the effect of each independent variable on the dependent variable.
Therefore, it is important to check for multicollinearity in a regression model and take steps to reduce it, such as removing one of the highly correlated independent variables or using regularization techniques. This can help to ensure that the regression model produces reliable estimates of the effects of the independent variables on the dependent variable.
for more questions on multicollinearity
https://brainly.com/question/17216244
#SPJ11
Can someone reflect (7,6) across the x axis then reflect across the y axis
Answers
Answer:
(7, -6)
(-7, -6).............
..
Answer: -7,-6
Step-by-step explanation:
So if we look at a graph 7,6 is on the right upper quadrant since its completely positiv, once we relfect the x axis then it becomes 7,-6 then once we reflect across the why axis it finally becomes -7,-6
You are facing north. You turn 45 degrees to your left. Take two steps forward. Turn 180 degrees. Turn 45 degrees to your right. Take one step back. Turn 90 degrees to your right. Which one of these statements is true?* You are facing the same direction you started. You are facing east. You are facing south. You are standing on the same spot you started out on. You are facing west.
Answers
Answer: Northeast - unless you are at the South Pole, in which case you are still facing North.
Step-by-step explanation
Sequence:
Facing North
90 degrees left = facing West
180 degrees right = facing East
reverse = facing West
45 degrees left = facing Southwest
reverse = facing Northeast
Eric rode his small motor bike 5 4/5 miles in 1/3 of an hour what is his average speed per mile
Answers
The Average speed is 17.4 mph.
What is Average speed?The average speed is calculated by dividing the total distance travelled by the total amount of motion time.
The overall distance the object covers in a given amount of time is its average speed. A scalar value represents the average speed. It has no direction and is indicated by the magnitude.
Average speed = Distance travelled/ Time taken
Given:
Distance = 5 4/5 = 29/5 miles
Time= 1/3 hours
So, Average speed = Distance travelled/ Time taken
Average speed= 29/5 x 3/1
= 87/5
= 17.4 mph
Hence, the Average speed is 17.4 mph.
Learn more about average speed here:
https://brainly.com/question/12322912
#SPJ1
solve the homogeneous differential equation in terms of x and y. a homogeneous differential equation is an equation of the form m(x, y) dx n(x, y) dy
Answers
To solve a homogeneous differential equation of the form m(x, y)dx + n(x, y)dy = 0, we can use the substitution y = vx.
By following the steps above, you can solve a homogeneous differential equation and obtain the solution in terms of x and y.
1. Compute the derivative of y with respect to x: dy/dx = v + x * dv/dx.
2. Substitute the values of y and dy/dx in the original equation: m(x, vx)dx + n(x, vx)(v + x * dv/dx)dx = 0.
3. Simplify the equation by dividing through by dx: m(x, vx) + n(x, vx)(v + x * dv/dx) = 0.
4. Rearrange the terms to isolate dv/dx: n(x, vx) * dv/dx = -m(x, vx) - n(x, vx) * v.
5. Divide through by n(x, vx): dv/dx = (-m(x, vx) - n(x, vx) * v) / n(x, vx).
6. This is now a separable differential equation. Separate the variables and integrate both sides: ∫(1 / n(x, vx)) dv = -∫[(m(x, vx) + n(x, vx) * v) / n(x, vx)] dx.
7. Integrate both sides with respect to v and x, respectively.
8. Solve for v.
9. Substitute the value of v back into the equation y = vx.
10. This will give you the general solution of the homogeneous differential equation in terms of x and y.
In conclusion, by following the steps above, you can solve a homogeneous differential equation and obtain the solution in terms of x and y.
To know more about homogeneous visit;
brainly.com/question/32618717
#SPJ11
Please help me I need to finish this :)

Answers
the gram-schmidt process produces from a linearly independent set {x1, x2, . . . , xp} an orthogonal set {v1, v2, . . . , vp} with the property that span{v1, . . . , vk}
Answers
The statement is true.
An orthogonal set with the same dimension as the initial collection of vectors is created by the Gram-Schmidt process.
Given that,
From a linearly independent collection of {x₁, x₂,..., xp}, the gram-Schmidt process creates an orthogonal set of {v₁, v₂,..., vp} with the feature that for each k, the vectors v₁...vk span the same subspace as that spanned by x₁...xk.
Whether the claim is true or false must be determined.
The statement is true.
An orthogonal set with the same dimension as the initial collection of vectors is created by the Gram-Schmidt process. An orthogonal set is further linearly independent. The orthogonal set produced by the Gram-Schmidt process and the original set will cover the same subspace if their dimensions are the same.
To learn more about orthogonal visit: https://brainly.com/question/2292926
#SPJ4
_____ placing research participants into the conditions of the experiment in such a way that each participant has an equal chance of being assigned to any level of the independent variable
Answers
Random assignment is the process of placing research participants into the conditions of an experiment in such a way that each participant has an equal chance of being assigned to any level of the independent variable.
Random assignment helps to ensure that the groups being compared in an experiment are equivalent at the start of the study, minimizing the influence of confounding variables and increasing the internal validity of the research.
By randomly assigning participants to different conditions, researchers can infer that any observed differences between groups after the experiment are due to the manipulation of the independent variable rather than preexisting differences between the groups.
Random assignment can be achieved through various methods, such as using random number tables, computer-generated randomization, or random assignment software.
It is an important aspect of experimental design and helps to strengthen the causal inferences that can be drawn from the research findings.
To know more about experimental design refer here:
https://brainly.com/question/28145500#
#SPJ11
Which statement must be true about the triangle below

Answers
Answer:
angle s equals to angle t
Step-by-step explanation:
the triangle is an isosceles triangle so...angle s equals to angle t
if a skip rope is a meter long and its a cm less how much is it pls answer
Answers
Answer:
99cm
Step-by-step explanation:
A meter is equal to 100cm
The rope is a metre (m) long but a centimetre (cm) less.
100cm - 1cm = 99cm
Xavier is driving home. He starts 250 miles from home and his car can travel 28 miles per gallon of gasoline he uses. Xavier stops at a rest stop that is 100 miles from home. Let g be the amount or gas he has used at that point. Set up and solve an equation for how much gas Xavier used to get to the rest stop.
Answers
Answer:
For 100 miles he uses 3.571 gallons of gasoline.
In equation form it is y/x*100
Step-by-step explanation:
Unitary Method
He travels 28 miles per gallon of gasoline.
For 1 mile he uses 1/28 gallons
For 100 miles he uses 1/28 * 100= 100/28= 3.571 gallons of gasoline.
Let x be the miles and y be the gallons of gasoline used to travel x miles.
Then for 1 mile the gallons of gasoline used will be y/ x gallons.
For 100 miles the gallons of gasoline used will be y/x *100 gallons.
In equation form it is y/x*100 gallons for 100 miles where x is the number of miles and y is the amount of gallons.
Line r passes through the points (1,1) and (8,9) . line s is perpendicular to r what is the slope of line s?
Answers
Answer: \(\frac{-7}{8}\)
Step-by-step explanation:
First, we will need to find the slope of line r.
\(\displaystyle \frac{y_{2} -y_{1} }{x_{2} -x_{1}} =\frac{9-1}{8-1}=\frac{8}{7}\)
Next, we know that perpendicular slopes are negative reciprocals of one another. To find the slope of line s, we will find the negative reciprocal of line r's slope.
\(\displaystyle \frac{8}{7} \rightarrow \frac{-7}{8}\)