suppose there are only two weather states: sunny and raining. If
today is sunny, the probability of raining for tomorrow is 0.6. If today is raining, the
probability of sunny for tomorrow is 0.7. Based on climatic records, during a year of 365
2
days, the number of sunny days is 265 days on average, and the remaining days are raining.
Please do the following
(1) What is the probability of sunny for tomorrow given today is sunny?
(2) What is the probability of raining for tomorrow given today is raining?
(3) Given today is sunny, what is the probability that yesterday is sunny as well?
Answers
Imagine there are only two possible weather conditions: sunny and rainy. If it's sunny today, there is a 0.6 percent probability it will rain tomorrow. If it rains today, there is a 0.7 percent probability that it will be sunny tomorrow. Based on climatic records, during a year of 365 2 days, the number of sunny days is 265 days on average, and the remaining days are raining.
Please do the following
(1) Given that today is sunny, what is the probability that tomorrow will be sunny?
(2) Given that it is raining today, what is the probability that it will rain tomorrow?
1. The probability of sunny for tomorrow given today is sunny is 0.4.
2. the probability of raining for tomorrow given today is raining is 0.3
Given that
If it's sunny today, there is a 0.6 percent probability it will rain tomorrow.
If it rains today, there is a 0.7 percent probability that it will be sunny tomorrow.
A year of 365 days, the number of sunny days is 265 days on average, and the remaining days are raining that are 100.
1. The probability of sunny for tomorrow given today is sunny is
1-0.6=0.4
2. the probability of raining for tomorrow given today is raining is
1-0.7=0.3
To learn more about probability visit: https://brainly.com/question/11234923
#SPJ9
Related Questions
Bennett Griffin and Chula Garza organized Cole Valley Book Store as a corporation; each contributed $71,500 cash to start the business and received 5,600 shares of common stock. The store completed its first year of operations on December 31, current year. On that date, the following financial items for the year were determined: December 31, current year, cash on hand and in the bank, $69,250; December 31, current year, amounts due from customers from sales of books, $43,500; unused portion of store and office equipment, $72,500; December 31, current year, amounts owed to publishers for books purchased, $12,400; one-year note payable to a local bank for $3,200. No dividends were declared or paid to the stockholders during the year.
Required:
Complete the following balance sheet as of the end of the current year. Some information has been given below.
What was the amount of net income for the year? (Hint: Use the retained earnings equation [Beginning Retained Earnings + Net Income − Dividends = Ending Retained Earnings] to solve for net income.)
Answers
he net income for the year is $16,550.
Calculation of the net income for the year:Retained earnings equation is:Beginning Retained Earnings + Net Income − Dividends = Ending Retained EarningsWhere, Beginning Retained Earnings = $0 (not given)Ending Retained Earnings = $16,550 (calculated from balance sheet)Dividends = $0 (not given)
Therefore,Net Income = Ending Retained Earnings - Beginning Retained Earnings + Dividends= $16,550 - $0 + $0= $16,550 Balance Sheet of Cole Valley Book Store as of December 31, current year:Current assets Cash on hand and in bank = $69,250 Amounts due from customers from sales of books = $43,500 Total current assets = $112,750 Property, plant, and equipment Unused portion of store and office equipment = $72,500
Total assets = $185,250Liabilities Amounts owed to publishers for books purchased = $12,400 One-year note payable to a local bank = $3,200 Total liabilities = $15,600 Stock holders' Equity Common stock, 5,600 shares at $71,500 = $400,400 Retained earnings, beginning = $0Net income = $16,550 Retained earnings, ending = $16,550 Total stockholders' equity = $416,950Total liabilities and stockholders' equity = $185,250 + $15,600 + $416,950= $617,800
for more search question income
https://brainly.com/question/30157678
#SPJ8
Which answers describe the shape below? Check all that apply.
31
A
A. Quadrilateral
B. Rhombus
C. Trapezoid
D. Parallelogram
E. Rectangle
F. Square

Answers
Answer:
A and D are correct. This is a parallelogram, which is a quadrilateral. B is not correct because not all the sides are congruent. C is not correct. E and F are not correct because this parallelogram does not have any right angles.
if one cup fills the jug to the second interval, how many cups do you need to fill the jug to 4?
Answers
2 cups you need to fill the jug to 4.
What is ratio?The ratio can be defined as the number that can be used to represent one quantity as a percentage of another. Only when the two numbers in a ratio have the same unit can they be compared. Ratios are used to compare two objects.
It depends on the size and markings of the jug.
If we assume that the jug is divided into equal intervals and each interval represents an equal volume,
then we can say that filling the jug to the second interval means that the jug is 1/2 full.
To fill the jug to the fourth interval, we need to fill the remaining 2 intervals, which means we need to add another 2 cups of liquid.
So, the answer is 2 cups.
Learn more about ratios here:
https://brainly.com/question/13419413
#SPJ9
Shawn wants to paint all the surfaces of the table shown below.
A. the volume of 3 rectangular prisms
B. the surface area of 1 triangle and 4 cylinders
C. the volume of 1 rectangular prism and 3 cylinders
D. the surface area of 2 triangles and 1 rectangular prism
What's the answer? How do I solve for this?!

Answers
the answer is D
The figure can be divided into a rectangle and 2 triangles
3/7 of which is 2 1/14
Answers
Answer:
Let the number be x
The statement is written as
\( \frac{3}{7}x = \frac{29}{14} \)
Multiply through by 14
That's
\( 14 \times \frac{3}{7} x = \frac{29}{14} \times 14\)
We get
2 × 3x = 29
6x = 29
Divide both sides by 6
That's
\( \frac{6x}{6} = \frac{29}{6} \)
\(x \: = \frac{29}{6} \: \: or \\ 4 \frac{5}{6} \)
Hope this helps you
Mrs. Pearce conducted a survey in her class on the ages of famous people. The table below shows the results of her survey. Guess Actual Age 15 28 25 28 39 50 36 24 42 56 45 72 80 Which equations could best represent the line-of-best-fit for the given data set?
Answers
Answer:
y=1.19x-4.3
Step-by-step explanation:
I did the math
Answer:
just here to steal some old points! sorry and thanks
Step-by-step explanation:
This problem considers maxima of functions f:C â R where f is a convex function and C CR"" is a convex set. (i) Assume f is a not the constant function over C. Show that f does not attain a maximum at any point in the int(C). (ii) Assume C is a compact convex set and that f is continuous and convex over C. Show that at least one maximizer is an extreme point of C. (Hint: Assume statement is false and prove a contradiction.)
Answers
1) The given statement " assuming f is not the constant function over c. So, f cannot attain a maximum in the interior of c." is truly proved and we have also
2) proved that "if c is a compact convex set, and f is a continuous convex function over c, then at least one maximizer is an extreme point of c" where f is convex function and c is convex set.
Assume that f is not a constant function over c and that f attains a maximum at some point x in the interior of c. Since x is in the interior of c, there exists a small enough ball B around x that is completely contained in the interior of c. Since f is convex, it is also continuous on c, so it is continuous on B. By the extreme value theorem, f attains a maximum on B at some point y. However, since f is not constant over c, there exists a point z in c such that f(z) > f(y). Since B is contained in the interior of c, z is not in B, and hence z is not equal to y. But this contradicts the fact that y is a maximum of f on B. Therefore, f cannot attain a maximum in the interior of c.
(ii) Assume that c is a compact convex set, f is continuous and convex over c, and that no maximizer is an extreme point of c. Since c is compact, there exists a finite set of extreme points {p1, p2, ..., pk} such that any point in c can be written as a convex combination of these extreme points. That is, for any x in c, there exist non-negative coefficients {a1, a2, ..., ak} such that x = a1p1 + a2p2 + ... + akpk, and a1 + a2 + ... + ak = 1.
Since none of the maximizers are extreme points, each maximizer x can be written as a convex combination of the extreme points with at least one non-zero coefficient. That is, for each maximizer x, there exists a set of indices {i1, i2, ..., im} such that x = b1p i1 + b2p i2 + ... + bm p im , where b j > 0 for all j and m < k.
Consider the set S = {x in c : f(x) ≥ f(p i1 ) for all i1 = 1, 2, ..., k}. Since f is continuous and c is compact, S is also compact. Moreover, since f(p i1 ) is a constant for each i1, S is a convex set.
We claim that S is non-empty. To see this, let x1 be any maximizer of f on c. Since x1 is not an extreme point, it can be written as a convex combination of some extreme points {p i1 , p i2 , ..., p im }. Since f(x1) is maximal, it must be that f(x1) ≥ f(p i1 ) for all i1. Hence x1 is in S, so S is non-empty.
Since S is a non-empty compact convex set, it has an extreme point x*. By the definition of S, we have f(x*) ≥ f(p i1 ) for all i1 = 1, 2, ..., k. We claim that x* is a maximizer of f on c.
Suppose not. Then there exists some point y in c such that f(y) > f(x*). By the convexity of f, there exists some t in (0,1) such that f(tx* + (1-t)y) > f(x*). Since x* is an extreme point of S and S is convex, it must be that tx* + (1-t)y is not in S. Therefore, there exists some i1 such that f(tx* + (1-t)y) < f(p i1 ). But this contradicts the fact that x* is an extreme point of S and f(x*) ≥ f(p i1 ) for all i1. Hence, x* is indeed a maximizer of f on c, and since x* is an extreme point of c, we have shown that at least one maximizer of f is an extreme point of c.
Therefore, we have proved that if c is a compact convex set, and f is a continuous convex function over c, then at least one maximizer is an extreme point of c.
To know more about convex function:
brainly.com/question/30340321
#SPJ4
For the polynomial function, describe the end behavior of its graph.
f(x) = 2x3 + 5x
Answers
Combine like terms.
9 + 12t – 6t
Question 3 options:
9 – 12t
21
21t
9 + 6t
Answers
The expression can be simplified to obtain as 9 + 6t.
What is an Algebraic expression?An algebraic expression can be obtained by doing mathematical operations on the variable and constant terms.
The variable part of an algebraic expression can never be added or subtracted from the constant part.
The given algebraic expression is 9 + 12t – 6t.
It can be simplified as follows,
9 + 12t – 6t
Here 9 is a constant.
And, the terms 12t and 6t have the same variable t.
Which implies they are like terms.
Since the like terms in an expression can be added to subtracted, the given expression can be simplified as below,
9 + 12t – 6t
⇒ 9 + 6t
Hence, the simplification of the given expression results as 9 + 6t.
To know more about algebraic expression click on,
brainly.com/question/953809
#SPJ1
i need help right now!!!

Answers
Answer:
I believe it would be 4x-8=-3x+13
Bookwork code: N84
Look at the poster below showing the price of pencils in a stationery shop.
Annabel wants to buy exactly 76 pencils. What is the lowest amount she can
pay?
Give your answer in pounds (£).
spar
..
Pencils for sale!
30p each
Pack of 10
pencils for £2
Answers
Based on mathematical operations, the lowest amount that Annabel can pay for pencils is $15.20
How is the lowest amount determined?The lowest amount that Annabel can pay for pencils can be determined using the mathematical operations of multiplication and division.
Multiplication and division are two of the four basic mathematical operations, including addition and subtraction.
If Annabel chooses to purchase the first pencil at 30p each, she would pay £22.80 (£0.30 x 76).
If Annabel chooses to purchase the second pencil class of a pack of 10 pencils for £2, she would pay £15.20 [£2 x (76 ÷ 10)].
Pencils for sale
30p each
Pack of 10 pencils for £2
Thus, if Annabel wants to buy the pencils, she can either pay £15.20 or £22.80, but using mathematical operations, the lowest amount she can pay is £15.20.
Learn more about mathematical operations at https://brainly.com/question/4721701.
#SPJ1
Robert earns $300 every week. What equation shows the relationship between salary per week (s), number of weeks worked (w), and total income (t).
w = 300 − 30
s − h = t
w − h − t = s
t = 300w
h = 300w
Answers
he entire graph of the function is shown in the figure below.
Write the domain and range of using interval notation.
Someone please help me. I really nee help. this question is due tonight before 8 and im stuck.

Answers
The given graph shows that the function is periodic and fluctuates between y = -2 and y = 2. So, the range of the function is [-2,2].
The graph covers one period, which is from x = -3 to x = 3, and then repeats itself indefinitely in both directions. So, the domain of the function is (-∞, ∞).
In general, the domain of a function consists of all the possible input values that the function can take. In this case, since the function repeats itself indefinitely, it can take any input value from negative infinity to positive infinity.
So, the domain is (-∞, ∞). The range of a function, on the other hand, consists of all the possible output values that the function can produce.
In this case, the function oscillates between y = -2 and y = 2, so the range is [-2,2]. The interval notation for the domain is (-∞, ∞) and for the range is [-2,2].
for such more questions on function
https://brainly.com/question/11624077
#SPJ8
The product of two fractions is 2/1/2 if one of the fraction is 7/1/2 find the other
Answers
Then, we have:
7/ 1/2 . x
= 2 / 1/2
Simplifying the left-hand side, we get:
7x = 4
Dividing both sides by 7, we get:
x = 4/7
Therefore, the other fraction is
4/7
if a line cuts the y-axis aty=-6 and the slope of the line is-10, find the equation of the line.
Answers
Answer:
y = -10x -6
Step-by-step explanation:
Among all pairs of numbers whose sum is 24, find a pair whose product is as large as possible. Show the work(the steps)! Write an equation of the corresponding quadratic function. How parabola opens? What is the maximum product? Does this function has a maximum value or the minimum value? Explain. Graph the function and upload the image.
Answers
The pair of numbers that yields the maximum product when their sum is 24 is (12, 12), and the maximum product is 144. The corresponding quadratic function is P(x) = -x^2 + 24x, and the parabola opens downwards.
To find a pair of numbers whose sum is 24 and whose product is as large as possible, we can use the concept of maximizing a quadratic function.
Let's denote the two numbers as x and y. We know that x + y = 24. We want to maximize the product xy.
To solve this problem, we can rewrite the equation x + y = 24 as y = 24 - x. Now we can express the product xy in terms of a single variable, x:
P(x) = x(24 - x)
This equation represents a quadratic function. To find the maximum value of the product, we need to determine the vertex of the parabola.
The quadratic function can be rewritten as P(x) = -x^2 + 24x. We recognize that the coefficient of x^2 is negative, which means the parabola opens downwards.
To find the vertex of the parabola, we can use the formula x = -b / (2a), where a = -1 and b = 24. Plugging in these values, we get x = -24 / (2 * -1) = 12.
Substituting the value of x into the equation y = 24 - x, we find y = 24 - 12 = 12.
So the pair of numbers that yields the maximum product is (12, 12). The maximum product is obtained by evaluating the quadratic function at the vertex: P(12) = 12(24 - 12) = 12(12) = 144.
Therefore, the maximum product is 144. This quadratic function has a maximum value because the parabola opens downwards.
To graph the function, you can plot several points and connect them to form a parabolic shape. Here is an uploaded image of the graph of the quadratic function: [Image: Parabola Graph]
For more such question on function. visit :
https://brainly.com/question/11624077
#SPJ8
The number line below represents which combined inequality? xs-6 orx 25 xs -6 and x 2 5 X2 -6 and x s 5 x2-6 or x s 5

Answers
Answer
Option C is correct.
x ≥ -6 and x ≤ 5
Explanation
In graphing inequality equations, the first thing to note is that whenever the equation to be graphed has (< or >), the circle at the beginning of the arrow is usually unshaded.
But whenever the inequality has either (≤ or ≥), the circle at the beginning of the arrow will be shaded.
Since the beginning of the blue mark is a shaded circle, the inequality is (≤ or ≥).
And considering that the region of the answer is between -6 and 5, it is evident that x is greater than or equal to -6 and less than or equal to 5. In mathematical terms,
x ≥ -6 and x ≤ 5
-6 ≤ x ≤ 5
Hope this Helps!!!
S-348
a-1.7 t
Area
Perimeter
Type
s = 3.3 yds
a = 1 65 yds
Area
Perimeter:
Type:
7)
s=5.4 mm
a = 2.57 mm
Area:
Perimeter:
Type:
Identify and Calculate the Area and Perimeter for ea
2)
a-8.2 yds
c-94 yds
Area
Perimeter.
Type:
5)
a
b
Ares
8)
a 66 cm
Triangle
h
Perimeter
Type.
Area
b-4.6 yds
a
h- 5.98 cm
Trapezoi
a=2.5 cm
a-1.25 cm
Perimeter
Type
Can someone solve help solve these???

Answers
Solve the system:
3x+6y=51
y=40-5x
Write down your solution here
Answers
Answer:
x=7 y=5
Step-by-step explanation:
3x+6(40-5x)=51
3x+240-30x=51
-27x+240=51
-27x=-189
27x=189
x=7
y=40-5(7)
y=40-35
y=5
You need to used the second equation and isolate either x or y. It’s your choice. Then, use that and substitute it in for the first equation. Then you will get an integer and substitute it back to the second equation.
HELPPPP THXX PLAAAAASSSSSSSS
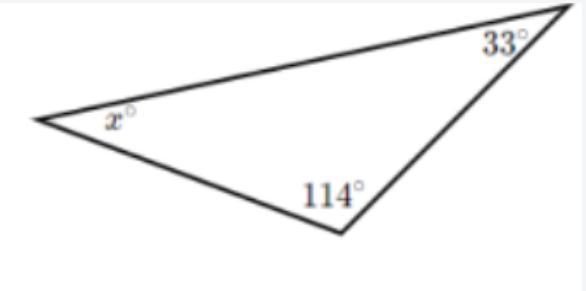
Answers
Answer:
43
Step-by-step explanation:
interior angles add up to 180
This is really important i have to get this one tomorrow please help me



Answers
A rancher has 200 feet of fencing to enclose two adjacent rectangular corrals. What dimensions should
be used so that the enclosed area will be a maximum?
Answers
Length is 33.33 feet and width is 25 feet are dimensions should
be used so that the enclosed area will be a maximum.
What is Area of Rectangle?The area of Rectangle is length times of width
Given that, a rancher has 200 feet of fencing to enclose two adjacent rectangular corrals of the same dimensions.
Here, the dimensions of the rectangles are the same.
The width of the two rectangles is W=2W+2W=4W
The length of the two rectangles is L=L+L+L=3L
Because the adjacent side has a common length.
3L+4W=200
3L=200-4W
Divide both sides by 3
L=(200-4W)/3
Let us form an equation using the area of rectangle formula:
A=2LW
=2(200-4W)/3.W
A=400-8W²/3
Let us differentiate to get the area to be maximized dA/dW=0
1/3×(400-8W²)=0
1/3(400-16W)=0
400-16W=0
400=16W
Divide both sides by 16
W=25
The width is 25 feet.
Substitute W value in equation to get L value:
L=200-4×25/3
=200-100/3
=100/3
=33.33
The length is 33.33 feet.
Now let us find the maximum area
A=2LW
=2×33.33×25
=1666.66
Hence, length is 33.33 feet and width is 25 feet are dimensions should
be used so that the enclosed area will be a maximum.
To learn more on Rectangle click:
https://brainly.com/question/20693059
#SPJ1
7 + 3x — 12х = 3x +1.
Answers
Point A is 3 units to the right of, and 20 units lower than, point B. Find the
slope of the line connecting points A and B.
O 20
3
O 20
3
O
-17
3
20
Answers
Answer:
02987329619
Step-by-step explanation:
02987329619
Answer:
kk
Step-by-step explanation:
Find angles A, B, C and D

Answers
Answer: a=101 b=79 c=83 d=97
Hello! I'm stuck here. I've tried solving it and I'm not getting any of the answers.

Answers
We have the cost function C(d) and the revenue function R(d) as:
\(C(d)=10500+3.9d\)\(\begin{gathered} R(d)=d(14.5-0.00003d) \\ R(d)=14.5d-0.00003d^2 \end{gathered}\)The profit can be defined as the difference between the revenue and the cost, so we can express it as:
\(\begin{gathered} P(d)=R(d)-C(d) \\ P(d)=(14.5d-0.00003d^2)-(10500+3.9d) \\ P(d)=-0.00003d^2+14.5d-3.9d-10500 \\ P(d)=-0.00003d+10.6d-10500 \end{gathered}\)We can now evaluate it for d = 30,000 as:
\(\begin{gathered} P=-0.00003\cdot(30,000)^2+10.6(30,000)-10,500 \\ P=-0.00003\cdot900,000,000+318,000-10,500 \\ P=-27,000+318,000-10,500 \\ P=280,500 \end{gathered}\)Answer: the profit for 30,000 units is $280,500 [Fourth option].
Plz help me!!!!! 3. &4 only!!!

Answers
Answer:
Step-by-step explanation:
3.
Note that
\(L_1 : 4x-y=10 \\ L_2: -2x+4y=16\)
aren't parralel lines. So they are intersected in one point.
Answer: Number of solutions is ONE. The system is soluble
4.
Similarly to 3. Number of solutions is ONE. The system is soluble
Suppose that the IQ of a randomly selected student from a university is normal with mean 115 and standard deviation 25. Determine the interval of values that is centered at the mean and for which 50% of the students have IQ's in that interval.
Answers
Answer:
The interval is [98,132]
Step-by-step explanation:
Normal Probability Distribution
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Normal with mean 115 and standard deviation 25.
This means that \(\mu = 115, \sigma = 25\)
Determine the interval of values that is centered at the mean and for which 50% of the students have IQ's in that interval.
Between the 50 - (50/2) = 25th percentile and the 50 + (50/2) = 75th percentile.
25th percentile:
X when Z has a p-value of 0.25, so X when Z = -0.675.
\(Z = \frac{X - \mu}{\sigma}\)
\(-0.675 = \frac{X - 115}{25}\)
\(X - 115 = -0.675*25\)
\(X = 98\)
75th percentile:
X when Z has a p-value of 0.75, so X when Z = 0.675.
\(Z = \frac{X - \mu}{\sigma}\)
\(0.675 = \frac{X - 115}{25}\)
\(X - 115 = 0.675*25\)
\(X = 132\)
The interval is [98,132]
The Kelly Students Council sold holiday swags for $10 for a fundraiser.. They spent $90 on materials to make the swags.. If they want to make at least $400,, how many swags do they need to sell? Write and solve the inequality.
Answers
Answer:
the answer would be 49
Step-by-step explanation:
they need to sell 49 to get their money back and make the 400 dollar goal
Use the drop-down menus below to represent the solution to the system of the two linear equations shown on the graph.
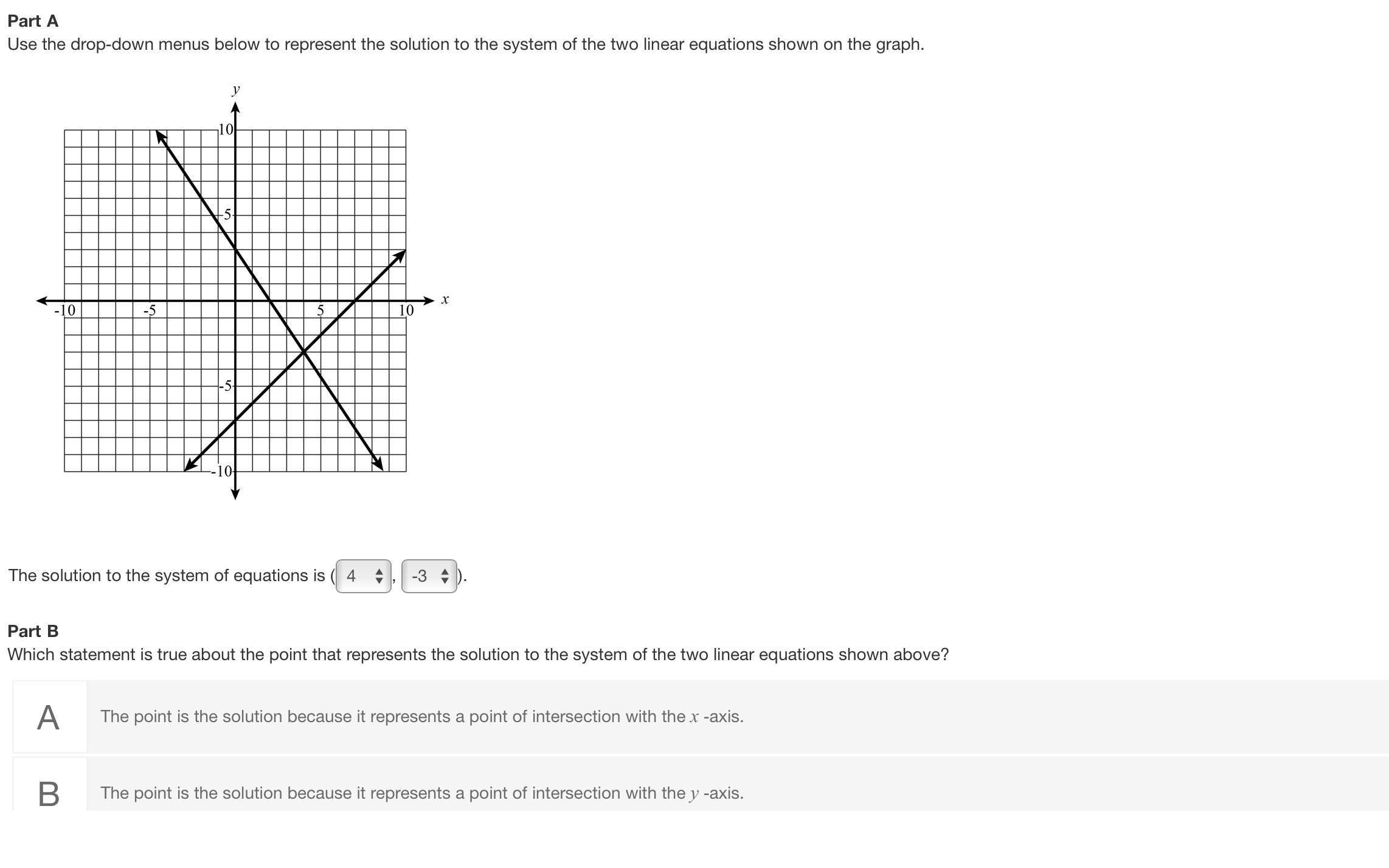

Answers
Answer:
• (a) (4, -3)
,• (b) Option C
Explanation:
Part A
Given the graph to the system of equations, the solution to the system is the point where the two lines intersect.
Tracing the points of intersection to the x and y-axis respectively, the solution to the system of equations is:
\((4,-3)\)Part B
The point that satisfies the solution to the system of two linear equations shown above is the solution because that is the only point that satisfies both equations simultaneously.
Option C is correct.