Suppose the distributor charges the artist a $50.00 cost for distribution, and the streaming services pay $5.00 per unit. (Note: One unit = one thousand streams)
Model the profit for the total number of streams by answering the questions below:
1. Use the cost for distribution to build the y-intercept. What is the y-intercept?
2. Use the payment per unit to build the slope. What is the slope?
3. What is the equation of this line?
4. After how many streams will the distributor charges be paid?
5. How many streams would it take to profit $950,000?
Answers
y-intercept of the function is (0, 50), the slope of the function is 5, the equation of the line is P(x) = 50 + 5x and it would take 189990 streams to profit $950,000.
What does math's intercept mean?The x-intercept and y-intercept are the points where a centre line the x- and y-axes, respectively.
Briefing:Given the following parameters
Fixed price = $50
The rate of change is $5 if streaming providers pay $ 5.00 per unit.
The necessary profit is provided as follows for the entire number of streams:
P(x) = 50 + 5x
The y-intercept is the location where x equals zero.
P(x) = 50 + 5x
P(0) = 50 + 5(0)
P(0) = 50
Thus, the function's y-intercept is (0, 50)
For the slope
mx = 5x
m = 5
Consequently, the function's slope is 5.
Equation of this line is P(x) = 50 + 5x
P(x) = 50 + 5x = 950000
5x = 950000 - 50
5x = 949950
x = 189990
Hence, it would take 189990 streams to profit $950,000.
To know more about intercept visit:
https://brainly.com/question/14180189
#SPJ1
Related Questions
Three friends — let’s call them X, Y , and Z — like to play pool (pocket billiards). There are some pool games that involve three players, but these people instead like to play 9-ball, which is a game between two players with the property that a tie cannot occur (there’s always a winner and a loser in any given round). Since it’s not possible for all three of these friends to play at the same time, they use a simple rule to decide who plays in the next round: loser sits down. For example, suppose that, in round 1, X and Y play; then if X wins, Y sits down and the next game is between X and Z. Question: in the long run, which two players square off against each other most often? Least often? So far what I’ve described is completely realistic, but now we need to make a (strong) simplifying assumption. In practice people get tired and/or discouraged, so the probability that (say) X beats Y in any single round is probably not constant in time, but let’s pretend it is, to get a kind of baseline analysis: let 0 < pXY < 1 be the probability that X beats Y in any given game, and define 0 < pXZ < 1 and 0 < pY Z < 1 correspondingly. Consider the stochastic process P that keeps track of
Answers
Answer:
Step-by-step explanation:
(a) If the state space is taken as \(S = \{(XY),(XZ),(YZ)\}\) , the probability of transitioning from one state, say (XY) to another state, say (XZ) will be the same as the probability of Y losing out to X, because if X and Y were playing and Y loses to X, then X and Z will play in the next match. This probability is constant with time, as mentioned in the question. Hence, the probabilities of moving from one state to another are constant over time. Hence, the Markov chain is time-homogeneous.
(b) The state transition matrix will be:
\(P=\begin{vmatrix} 0 & p_{XY} & (1-p_{XY})\\ p_{XZ}& 0& (1-p_{XZ})\\ p_{YZ}&(1-p_{YZ}) & 0\end{vmatrix},\)
where as stated in part (b) above, the rows of the matrix state the probability of transitioning from one of the states \(S = \{(XY),(XZ),(YZ)\}\) (in that order) at time n and the columns of the matrix state the probability of transitioning to one of the states \(S = \{(XY),(XZ),(YZ)\}\) (in the same order) at time n+1.
Consider the entries in the matrix. For example, if players X and Y are playing at time n (row 1), then X beats Y with probability \(p_{XY}\), then since Y is the loser, he sits out and X plays with Z (column 2) at the next time step. Hence, P(1, 2) = \(p_{XY}\). P(1, 1) = 0 because if X and Y are playing, one of them will be a loser and thus X and Y both together will not play at the next time step. \(P(1, 3) = 1 - p_{XY}\), because if X and Y are playing, and Y beats X, the probability of which is\(1 - p_{XY}\), then Y and Z play each other at the next time step. Similarly,\(P(2, 1) = p_{XZ}\), because if X and Z are playing and X beats Z with probability\(p_{XZ}\), then X plays Y at the next time step.
(c) At equilibrium,
\(vP = v,\)
i.e., the steady state distribution v of the Markov Chain is such that after applying the transition probabilities (i.e., multiplying by the matrix P), we get back the same steady state distribution v. The Eigenvalues of the matrix P are found below:
\(:det(P-\lambda I)=0\Rightarrow \begin{vmatrix} 0-\lambda & 0.6 & 0.4\\ 0.975& 0-\lambda& 0.025\\ 0.95& 0.05& 0-\lambda\end{vmatrix}=0\)
\(\Rightarrow -\lambda ^3+0.9663\lambda +0.0337=0\\\Rightarrow (\lambda -1)(\lambda ^2+\lambda +0.0337)=0\)
The solutions are
\(\lambda =1,-0.0349,-0.9651.\) These are the eigenvalues of P.
The sum of all the rows of the matrix\(P-\lambda I\) is equal to 0 when \(\lambda =1.\)Hence, one of the eigenvectors is :
\(\overline{x} = \begin{bmatrix} 1\\ 1\\ 1 \end{bmatrix}.\)
The other eigenvectors can be found using Gaussian elimination:
\(\overline{x} = \begin{bmatrix} 1\\ -0.9862\\ -0.9333 \end{bmatrix}, \overline{x} = \begin{bmatrix} -0.0017\\ -0.6666\\ 1 \end{bmatrix}\)
Hence, we can write:
\(P = V * D * V^{-1}\), where
\(V = \begin{bmatrix} 1 & 1 & -0.0017\\ 1 & -0.9862 & -0.6666 \\ 1 & -0.9333 & 1 \end{bmatrix}\)
and
\(D = \begin{bmatrix} 1 & 0 & 0\\ 0 & -0.9651 & 0 \\ 0 & 0 & -0.0349 \end{bmatrix}\)
After n time steps, the distribution of states is:
\(v = v_0P^n\Rightarrow v = v_0(VDV^{-1})^n=v_0(VDV^{-1}VDV^{-1}...VDV^{-1})=v_0(VD^nV^{-1}).\)
Let n be very large, say n = 1000 (steady state) and let v0 = [0.333 0.333 0.333] be the initial state. then,
\(D^n \approx \begin{bmatrix} 1 & 0 & 0\\ 0& 0 &0 \\ 0 & 0 & 0 \end{bmatrix}.\)
Hence,
\(v=v_0(VD^nV^{-1})=v_0(V\begin{bmatrix} 1 & 0 & 0\\ 0 &0 &0 \\ 0& 0 & 0 \end{bmatrix}V^{-1})=[0.491, 0.305, 0.204].\)
Now, it can be verified that
\(vP = [0.491, 0.305,0.204]P=[0.491, 0.305,0.204].\)
answers for the homework
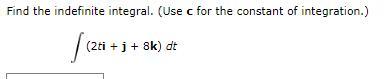
Answers
The indefinite integral of ∫(2ti+j+8k)dt is t²i +tj+8tk+c.
Given the expression is ∫(2ti+j+8k)dt
The indefinite integrals, also known as the derivatives of functions, are integrals that can be computed using the process of differentiation in reverse.
Further approaches for resolving indefinite integrals include integration by parts, substitution, integration of partial fractions, and integration of inverse trigonometric functions.
now, ∫(2ti+j+8k)dt
= 2t²/2 i + tj +8tk
= t²i +tj+8tk+c
hence we get the indefinite integral as t²i +tj+8tk+c
Learn more about Indefinite integral here:
brainly.com/question/22008756
#SPJ1
I would really appreciate some help. Thanks!
Seth has game and education apps on his tablet. He noticed that he has 5 game apps for every 2 education apps. Which of the following is another way to write this ratio?
A. 2:3
B. 2:5
C. 3:2
D. 5:2
Answers
Answer:
D
Step-by-step explanation:
the question says that he has 5 to 2 and if you put it in a fraction you cant reduce it so therefore the answer has to be 5:2
Answer:
D. 5:2
Step-by-step explanation:
He has 5 games so 5: for every 2 school apps so 5:2
PLEASE HELP ASAP! DUE SOON !

Answers
Answer & Step-by-step explanation:
The domain of the function g(x) = ⟨÷⟩6x + 6 is the set of all real numbers, since dividing by zero is not defined.
And it is a linear function, which means that it is a straight line in a 2-dimensional graph. The slope of the line is 6, and the y-intercept is 6, meaning that when x=0, the value of g(x) is 6.
Helppppppppp pleaseeee ASAP

Answers
Answer:
y = (x + 4)^2 - 3
Use Foil to solve (x + 4):
(x + 4)(x + 4) = x^2 + 8x + 16
Plug it back into original equation:
y = x^2 + 8x + 16 - 3
y = x^2 + 8x + 13 is the answer :)
PLS HELP ASAP THIS IS DUE NOW!!!!

Answers
Answer:
Trapezoid, rectangle, rhombus
Step-by-step explanation:
hope this helps!
Which expression is equivalent to
-32 3/5
-8
-3/325
3/325
1/8
Answers
Answer:
\(-32^\frac{3}{5} = -8\)
Step-by-step explanation:
Given
\(-32^\frac{3}{5}\)
Required
The equivalent expression
We have:
\(-32^\frac{3}{5}\)
Rewrite as:
\(-32^\frac{3}{5} = (-32)^\frac{3}{5}\)
Expand
\(-32^\frac{3}{5} = (-2^5)^\frac{3}{5}\)
Remove bracket
\(-32^\frac{3}{5} = -2^\frac{5*3}{5}\)
\(-32^\frac{3}{5} = -2^3\)
\(-32^\frac{3}{5} = -8\)
After the introduction of a new soft drink, 200 people are asked to take a taste test to see how it is being received. Of those who participated, 48 said they preferred the new soft drink, 112 preferred the old soft drink, and 40 could not tell any difference. What is the probability that a person in this survey, chosen at random, preferred the new soft drink
Answers
Answer:
Step-by-step explanation:
The possibility is 48/200
The probability of people preferred the new soft drink is 6/25.
To find the probability.
What is probability?probability is the ratio of the number of favorable outcomes and the total number of possible outcomes.
Given that:
Total number of people taste test=200
Number of people who participated new soft drink=48
Number of people who participated old soft drink=112
Number of people who participated could not tell any difference=40
So, the probability of people preferred the new soft drink=
favorable outcome/total number of outcome
probability of people preferred the new soft drink=48/200
probability of people preferred the new soft drink=6/25
So, the probability of people preferred the new soft drink is 6/25.
Learn more about probability here:
https://brainly.com/question/23471143
#SPJ2
Pls send only answers - no work




Answers
Answer:
No
Step-by-step explanation:
If you are just seeking answers, you are basically cheating and trying to get someone to do your work...which will not help you learn the material ....sad.
Use properties to find the sum or product.1. 6 X 892. 93 +(68 +7)3. 5 X 23 X 24. 8 X 51 5. 34 + 0 + 18+ 26 6. 6 X 107
Answers
3. We want to solve using properties;
\(\begin{gathered} 5\times23\times2 \\ =5\times2\times23 \\ =5\times2\times(20+3) \\ =10\times(20+3) \\ =(10\times20)+(10\times3) \\ =200+30 \\ =230 \end{gathered}\)It simply involve trying to reduce numbers to their simpliest form to make multiplication and addition easy without using calculator.
like; 21=20+1, 39=40-1 etc.
4. Given;
\(\begin{gathered} 8\times51 \\ =8\times(50+1) \\ =8\times50+8\times1 \\ =400+8 \\ =408 \end{gathered}\)in the formula C= prn, p stands for
A. percent
B. period
C. price per item
D. promotion
Answers
Answer:
C.
Step-by-step explanation:
The sum of a number x and -7 is less than or equal to 18.
Answers
Step-by-step explanation:
x + (-7) ≤ 18
x - 7 ≤ 18
x ≤ 18 + 7
x ≤ 25
Value of x is less than or equal to 25
Find the volume of a right circular cone that has a height of 11.4 in and a base with a radius of 5.1 in. Round your answer to the nearest tenth of cubic inch.
Answers
Answer:
155.3"^3
Step-by-step explanation:
the volume of a cone: 1/3 \(\pi\)r^2 h
the volume of a right circular cone will be
1/3 \(\pi\)(5.1)^2 * 11.4
310.60 for a full circular cone.
for a right circular cone, we use 90/180 of the volume.
= 155.3
The volume of the cone is 121.8 in³.
A cone is a 3-dimensional shape that consists of a flat circular base and a tip known as the vertex.
Volume of a cone = \(\frac{1}{3}\)πr²h
Where:
π = pi = 22/7
r = radius
h = height
Volume = \(\frac{1}{3}\) x 22/7 x 5.1² x 11.4 = 121.8 in³
To round off to the nearest tenth, if the hundredth figure is greater or equal to 5, add to the tenth figure, if this is not the case, the tenth figure remains unchanged.
To learn more about how to determine the volume of a cone, please check: https://brainly.com/question/14273451
what is the equation for the perpendicular bisector of the line segment whose endpoints are (-7, 2) and (-1,-6)
Answers
The equation of the perpendicular bisector of the line segment with endpoints (-7, 2) and (-1, -6) is y = (3/4)x + 1.
To find the equation of the perpendicular bisector of a line segment, we need to determine the midpoint of the line segment and the slope of the line segment. The perpendicular bisector will have a negative reciprocal slope compared to the line segment and will pass through the midpoint.
Given the endpoints (-7, 2) and (-1, -6), we can find the midpoint using the midpoint formula:
Midpoint = ((x1 + x2)/2, (y1 + y2)/2)
Midpoint = ((-7 + (-1))/2, (2 + (-6))/2)
= (-8/2, -4/2)
= (-4, -2)
The midpoint of the line segment is (-4, -2).
Next, we need to find the slope of the line segment using the slope formula:
Slope = (y2 - y1)/(x2 - x1)
Slope = (-6 - 2)/(-1 - (-7))
= (-6 - 2)/(-1 + 7)
= (-8)/(6)
= -4/3
The slope of the line segment is -4/3.
Since the perpendicular bisector has a negative reciprocal slope, the slope of the perpendicular bisector will be 3/4.
Now, we can use the midpoint (-4, -2) and the slope 3/4 in the point-slope form of a line to find the equation of the perpendicular bisector:
y - y1 = m(x - x1)
y - (-2) = (3/4)(x - (-4))
y + 2 = (3/4)(x + 4)
y + 2 = (3/4)x + 3
y = (3/4)x + 1.
For more such questions on Line segment:
https://brainly.com/question/2437195
#SPJ8
Read the following prompt and type your response in the space provided.
Describe the relationship between the probability of an event and its complement.
If the probability of an event is 0.95, what is the probability of its complement?
Answers
The probability of the complement of the event is 0.05.
The complement of an event is the probability of that event not occurring. The relationship between the probability of an event and its complement is that they always add up to 1.
Therefore, if the probability of an event occurring is p, then the probability of its complement not occurring is 1-p.
In the case where the probability of an event is 0.95, the probability of its complement not occurring would be 1-0.95 = 0.05. This means that the probability of the complement of the event is 0.05.
This concept is important in probability theory and is used to calculate the probabilities of events and their complements. It allows us to consider all possible outcomes of a given situation and calculate the likelihood of each of them.
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
Question 3
2 pts
1 km = 0.62 mi. The distance between Lowell and Shelby is 280 miles. How many
kilometers is this?
Round your answer to the nearest whole kilometer.
Do not include "km" with your response; provide just a numeric answer.
Answers
Answer:450.61
Step-by-step explanation:
How do I solve for this?

Answers
Answer: \(cosx =- \sqrt{ 1 - sin^2x}\)
Step-by-step explanation:
Generally speaking; \(cos^2x + sin^2x = 1\)
rearranging this gives us all sorts of cool things.
for now, we will use: \(cosx = \sqrt{ 1 - sin^2x}\)
This however, is general.
In the third quadrant, cosine is negative. So cosx in QIII will be:
\(cosx =- \sqrt{ 1 - sin^2x}\)
and thats the answer :)
A penguin walks 10 feet in 6 seconds. At this speed:
How far does the penguin walk in 45 seconds?
How long does it take the penguin to walk 45 feet?
Explain or show your reasoning.
PLS KEEP THIS SIMPLE LIKE A 6TH GRADE ANSWER I JUST WANT TO KNOW THIS
Answers
Answer: The penguin will walk 75.15 feet in 45 sec
Answer:653745
Step-by-step explanation:
Determine if the waveform has dc, even, or odd symmetry. (b) Obtain its cosine/sine Fourier series representation.
Answers
Answer and Step-by-step explanation:
Solution:
(a)
The waveform has even symmetry.
(b) Obtain its cosine/sine Fourier series representation.
Given:
Period = T = 4 s
W0 = 2π/ T = π / 2 rad/s
F(t) = { -5t( -2≤t≤5t 0s≤ t ≤2s )}
a0= 1/ T ∫_(-t/2)^(t/2)f(t)dt
= 1/4 [ ∫_(-2)^0〖-5tdt+ ∫_0^25tdt〗]
= 1/4 [5/2 x 4 + 5/2 x 4]
= 1/4 [20 /2 + 20 / 2]
= 1/4 [10 + 10]
= 1/4 (20)
= 5
An= 2/T ∫_(-t/2)^(t/2)〖f(t)cos(nw0t)dt〗
= 1/2 [∫_(-2)^0〖-5tcos(nπ/2)tdt+ ∫_0^2〖5tcos(nπ/2)tdt〗〗]
= 20 / n2π2 [ cos(nπ) – 1]
Bn = 0
(Even symmetry)
F(t) = 5 + Ʃn=1∞ 20 / n2π2 [ cos(nπ) -1] (cos (nπ/2)t)

Calvin estimated he would need 8 hours to
complete his science project. It actually took
him 12 1/2 hours to get everything done. What
was his percent error?
Answers
Answer:45%
Step-by-step explanation:
Hope this helps.
I’m not really good at percentages but I’m sorry I couldn’t give you the full answer. You got this though! <3
Select the correct answer.
Evaluate the following expression when x = -4 and y = 4.
x
6
−
x
4
y
A.
1
,
025
4
B.
1
,
023
4
C.
16
,
385
4
D.
−
1
,
023
4

Answers
Answer:
1023/4
Step-by-step explanation:
shown in the picture

Write the fraction or mixed number as a percent.
2 3/10
Answers
Answer:
230%
Step-by-step explanation:
2x3/10=23/10=2.3x100%=230%
Find the probability that a randomly selected point within the square falls in the red shaded square

Answers
The probability that a randomly selected point within the square falls in the red shaded square is 1/16
What is probability?A probability is a number that reflects the chance or likelihood that a particular event will occur. The certainty of an event to occur is 1 and it is 100% in percentage.
Probability = sample space /total outcome
sample space is the area of the red shaded square and the total outcome is the big square.
Area of red shaded square = 1 × 1 = 1unit²
area of the big square = 4 × 4 = 16 units²
Therefore the probability that a point selected falls on the red shaded square
= 1/16
learn more about probability from
https://brainly.com/question/24756209
#SPJ1
Only answer if you know the real answer please appreciate it answer question number 2 please

Answers
Answer:
0.99
Step-by-step explanation:
Median is the middle term (or mean of the middle two terms) of a series arranged in order of magnitude.
Here the weights are already arranged in order and the middle term is 0.99
Therefor the median = 0.99
Help me please pleasessssss

Answers
2/3 - 6 please show your work
Answers
Answer:
\(\frac{-16}{3} or -5\frac{1}{3}\)
Step-by-step explanation:
\(\frac{2}{3} - 6\) We know that if you add \(\frac{1}{3}\) to \(\frac{2}{3}\\\) it will equal 1.
You need to use that knowledge to solve this problem easier.
So... you have negative six, add \(\frac{2}{3}\\\) to it.
You should get the number \(\frac{-16}{3}\)
Let me know if you need more help!
Triangle ABC was dilated using the rule DO,4. Triangle A'B'C' is the result of the dilation.
Point O is the center of dilation. Triangle A B C is dilated to create triangle A prime B prime C prime. The length of O B is three-fourths.
What is OB'?
1.5 units
3 units
4.5 units
6 units
Mark this and return
Answers
Answer:
(b) 3 units
Step-by-step explanation:
You want to know the length of OB' when OB = 3/4 and ∆ABC is dilated about point O by a factor of 4.
DilationThe dilation factor multiplies every length.
If OB is 3/4, then OB' is 4(3/4) = 3.
The length of OB' is 3 units.
<95141404393>
Find the value of y when
2x. + 6y = 1
Fast please!!!???
Answers
6y = -2x+1
Divide all the number with 6
Y = -1/3 + 1/6 or 1.7
What is an example of "an enumeration of its range {aξ : ξ < α}"?

Answers
An example of "an enumeration of its range {aξ : ξ < α}" in this case would be the list of natural numbers {0, 1, 2, 3, ...}, which represents the ordinal numbers less than ω^2.
How to determine an example of "an enumeration of its range {aξ : ξ < α}"An example of "an enumeration of its range {aξ : ξ < α}" can be found in the context of ordinal numbers.
Let's consider the ordinal number α = ω^2, where ω represents the first infinite ordinal (the set of all natural numbers). In this case, the range {aξ : ξ < α} refers to the collection of all ordinal numbers that are less than α.
The ordinal numbers less than ω^2 can be enumerated as follows:
a0 = 0
a1 = 1
a2 = 2
...
an = n
...
Each natural number n corresponds to an ordinal number less than ω^2. The enumeration continues indefinitely, as there are infinitely many ordinal numbers less than ω^2.
So, an example of "an enumeration of its range {aξ : ξ < α}" in this case would be the list of natural numbers {0, 1, 2, 3, ...}, which represents the ordinal numbers less than ω^2.
Learn more about range at https://brainly.com/question/26098895
SPJ1
What percent of 500 is 20?
Answers
Answer: 4%
Step-by-step explanation:
To answer this question we will put the total (500) in the denominator and the portion (20) in the numerator. Then we will divide.
20 / 500 = 0.04
Next, a decimal multiplied by 100 becomes a percent.
0.04 * 100 = 4%