Suppose that an Internal Revenue Service (IRS) representative claims that the average tax deduction for medical care is $1,250, and assume that this variable is normally distributed. A taxpayer who believes that the deduction might be less than $1,250 decides to randomly sample 12 families who have an average deduction of $934 with a standard deviation of $616. a. What are the null and alternative hypotheses? b. What is the value of the test statistic, i.e. t-stat, in this example? Show your work. c. What is the p-value associated with this test statistic? (HINT: you have less than 30 observations so you will need to use t-table to obtain critical values.) d. What can you conclude at the 10-percent level of significance? What can you conclude at the 5-percent level of significance? Explain. (HINT: you have less than 30 observations so you will need to use t-table to obtain critical values.)
Answers
Step-by-step explanation:
We have bar x = 934
S = 616
n = 12
A.
Null hypothesis: h0: u = 1250
Alternative hypothesis: h1: u< 1250
B. To get the t test statistic
T = 934-1250/616/√12
T = -316/616/3.4641
= -316/117.824
= -1.777
C. O value = p(t<-1.777)
This gives 0.0516
D. At 10% significance
O.0516<0.1 so we reject the null hypothesis and conclude that this deduction is < than 1250
At 5% level of significance
O.o516>0.05. we do not reject the null hypothesis. We conclude there is insufficient evidence of claim being less than 1250
Related Questions
Let V denote the set of all differentiable real-valued functions defined on the real line. Prove that V is a vector space with the operations of addition and scalar multiplication.
Answers
V is a vector space with the operations of addition and scalar multiplication.
Since f(t) and g(t) are real numbers, you're utilizing the fact that the real numbers themselves are commutative in that step, which truly confused me when I first learned about it and after.
Let V denote the set of all differentiable real-valued functions defined on the real line.
You only need to mention that real-number addition is commutative. Since f is not a number until you evaluate, you couldn't do it before you did.
On a different note, you cannot say that
f+g=f(t)+g(t)
but you can say that (f+g)(t)=f(t)+g(t)
So V is a vector space with the operations of addition and scalar multiplication.
Know more about scalar multiplication
https://brainly.com/question/26649852
#SPJ4
If C(x) = 16000 + 600x − 1.8x2 + 0.004x3 is the cost function and p(x) = 4200 − 6x is the demand function, find the production level that will maximize profit. (Hint: If the profit is maximized, then the marginal revenue equals the marginal cost.)
Answers
Answer:
Quantity that will maximize profit=1000
Step-by-step explanation:
Assume quantity=x
Revenue=price*quantity
=(4200-6x)x
=4200x-6x^2
Marginal revenue(MR) =4200-12x
Cost(x)= 16000 + 600x − 1.8x2 + 0.004x3
Marginal cost(MC) =600-3.6x+0.012x^2
Marginal cost=Marginal revenue
600-3.6x+0.012x^2=4200-12x
600-3.6x+0.012x^2-4200+12x=0
0.012x^2-8.4x-3600=0
Solve the quadratic equation using
x= -b +or- √b^2-4ac/2a
a=0.012
b=-8.4
c=-3600
x=-(-8.4) +or- √(-8.4)^2- (4)(0.012)(-3600) / (2)(0.012)
= 8.4 +or- √70.56-(-172.8) / 0.024
= 8.4 +or- √70.56+172.8 / 0.024
= 8.4 +or- √243.36 / 0.024
= 8.4 +or- 15.6/0.024
= 8.4/0.024 +15.6/0.024
= 350+650
x=1000
OR
= 8.4/0.024 -15.6/0.024
= 350 - 650
= -300
x=1000 or -300
Quantity that maximises profits can not be negative
So, quantity that maximises profits=1000
For each ordered pair (x, y), determine whether it is a solution to the inequality y≤0.
(8,-43)
(4.-22)
(-3,25)
(-7,45)
Is it a solution?
Answers
Answer:
(8,-43)
(4,-22)
Step-by-step explanation:
In order for the ordered pair to be a solution of the inequality, you must be able to plug in the y-value of the ordered pair and it must be less than or equal to 0.
For example:
(4,-22)
x=4 ; y=-22
Plug y into the inequality
y≤0
-22≤0
Since the statement is true, I know that (4,-22) must be a solution to the inequality.
Another way to solve this problem is by graphing. If an ordered pair is in the shaded region, it is a solution to the inequality. Attached is a graph of both the inequality and ordered pairs plotted.
If this answer helped you, please leave a thanks or a Brainliest!!!
Have a GREAT day!!!

Answer:
Step-by-step explanation:
To determine whether each ordered pair is a solution to the inequality y ≤ 0, we need to check if the y-coordinate of each pair is less than or equal to zero.
Let's check each ordered pair:
(8, -43):
The y-coordinate is -43. Since -43 is less than zero, this ordered pair is a solution to the inequality y ≤ 0.
(4, -22):
The y-coordinate is -22. Since -22 is less than zero, this ordered pair is a solution to the inequality y ≤ 0.
(-3, 25):
The y-coordinate is 25. Since 25 is greater than zero, this ordered pair is not a solution to the inequality y ≤ 0.
(-7, 45):
The y-coordinate is 45. Since 45 is greater than zero, this ordered pair is not a solution to the inequality y ≤ 0.
So, the solutions to the inequality y ≤ 0 are:
(8, -43) and (4, -22).
En la final de un concurso escolar de
matemática participan 6 alumnos de los
cuales 3 son alumnos del colegio A. Si se
premia a los dos primeros con regalos
diferentes, entonces la probabilidad de que
los alumnos del colegio A obtengan los dos
premios (no hay empates), es:
Answers
Usando la distribución hipergeométrica, la probabilidad de que los alumnos del colegio A obtengan los dos premios (no hay empates), es: 0.2 = 20%.
¿Qué es la fórmula de distribución hipergeométrica?La fórmula es:
\(P(X = x) = h(x,N,n,k) = \frac{C_{k,x}C_{N-k,n-x}}{C_{N,n}}\)
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
Los parámetros son:
x es el número de éxitos.N es el tamaño de la población.n es el tamaño de la muestra.k es el número total de resultados deseados.Los valores de los parámetros son:
N = 6, k = 3, n = 2.
La probabilidad de que los alumnos del colegio A obtengan los dos premios (no hay empates), es P(X = 2), por eso:
\(P(X = x) = h(x,N,n,k) = \frac{C_{k,x}C_{N-k,n-x}}{C_{N,n}}\)
\(P(X = 2) = h(2,6,2,3) = \frac{C_{3,2}C_{3,0}}{C_{6,2}} = 0.2\)
Puede-se aprender más a cerca de la distribución hipergeométrica en https://brainly.com/question/24826394
#SPJ1
Study the solutions of the three equations on the right. Then, complete the statements below. There are two real solutions if the radicand is There is one real solution if the radicand is There are no real solutions if the radicand is 1. y = negative 16 x squared + 32 x minus 10. x = StartFraction negative 32 plus-or-minus StartRoot 384 EndRoot Over negative 32 EndFraction. 2. y = 4 x squared + 12 x + 9. x = StartFraction negative 12 plus-or-minus StartRoot 0 EndRoot Over 8 EndFraction. 3. y = 3x squared minus 5 x + 4. x = StartFraction 5 plus-or-minus StartRoot negative 23 EndRoot Over 6 EndFraction.
Answers
Answer:
There are two real solutions if the radicand is
✔ positive.
There is one real solution if the radicand is
✔ zero.
There are no real solutions if the radicand is
✔ negative.
Step-by-step explanation:
ON MY DOG KIDS DIS RIGHT
Answer:
1.Postieve
2.Zero
3.Negative.
Step-by-step explanation
i did it on ed and got it right.
Desperate Need Of Help

Answers
The domain and range of the graph above in interval notation include the following:
Domain = [-6, 3]
Range = [-3, 3]
What is a domain?In Mathematics and Geometry, a domain refers to the set of all real numbers (x-values) for which a particular function (equation) is defined.
In Mathematics and Geometry, the horizontal portion of any graph is used to represent all domain values and they are both read and written from smaller to larger numerical values, which simply means from the left of any graph to the right.
By critically observing the graph shown in the image attached above, we can reasonably and logically deduce the following domain and range:
Domain = [-6, 3] or -6 ≤ x < 3.
Range = [-3, 3] or -3 < y < 3
Read more on domain here: brainly.com/question/9765637
#SPJ1
quater of 80? its for my maths, thanks xx
Answers
explanation
20*4= 80
hope i helped!
Quarter of 80:
= 80 x 1/4
= 80/4
= 20
Brand A has a box of 25 forks for 1.99 and Brand B has a box of 42 totals for 3.89. What is the unit price for each brand and what brand is a better buy based on unit price
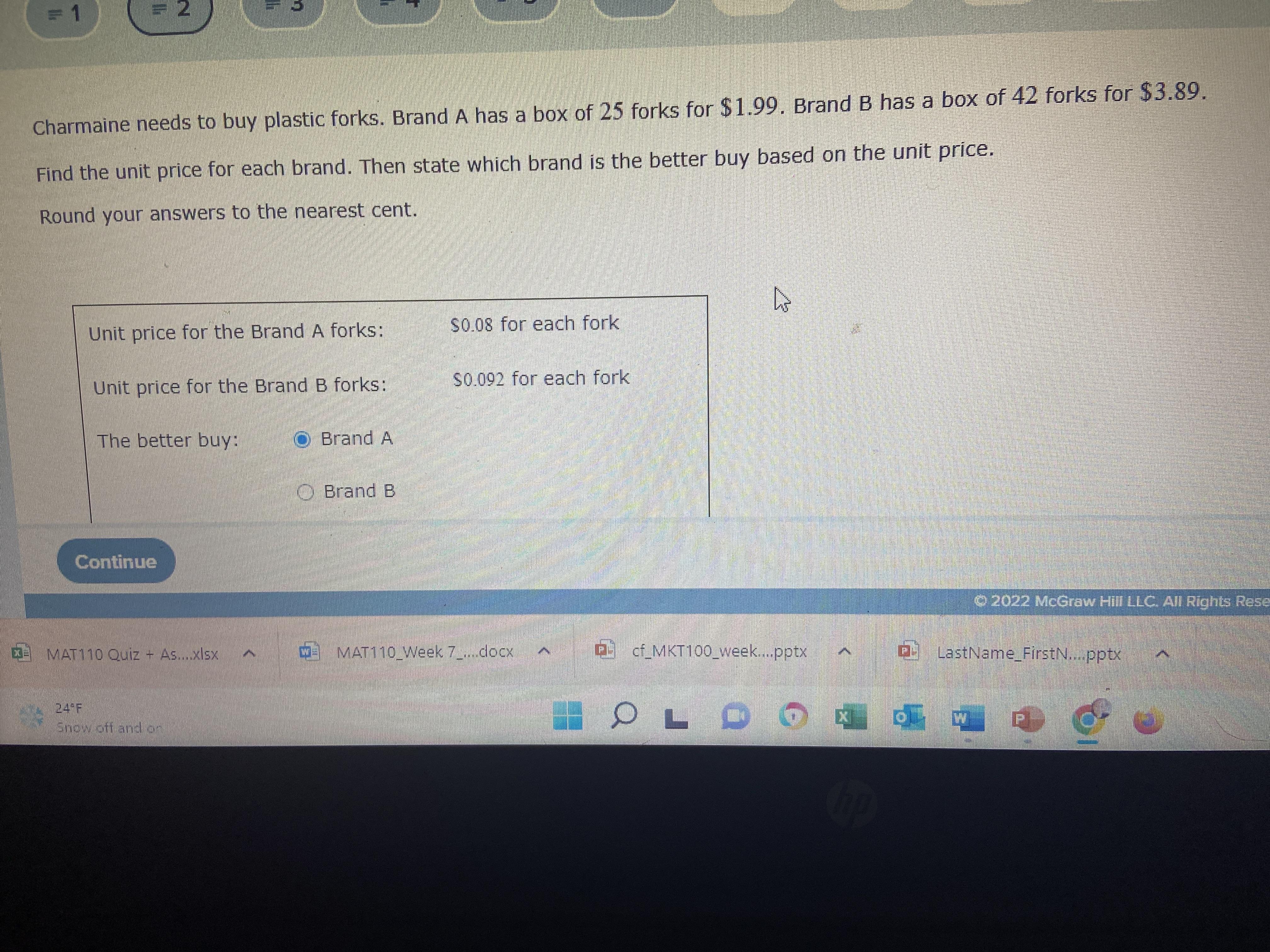
Answers
Answer:
Brand A
Step-by-step explanation:
Brand A has a box of 25 forks for 1.99
Take the price per fork
1.99 /25 = .0796
.08 per fork
Brand B has a box of 42 totals for 3.89
3.89 / 42
.092319048
.09 per fork
25 points! Please help! Will give brainliest to correct answer!

Answers
Answer:
I think AC is 6.
Step-by-step explanation:
This looks like an equilateral triangle so that means because there is a 3 on one side of the line it should be the same on the other side of the line so 3 x 2 = 6.
Step-by-step explanation:
\(triangle \: abd \\ using \: pythagoras \: theorem \\ {hyp}^{2} = {adj}^{2} + {opp}^{2} \\ {12}^{2} = {3}^{2} + {opp}^{2} \\ 144 = 9 + {x}^{2} \\ 144 - 9 = {x}^{2} \\ 135 = {x}^{2} \\ take \: the \: square \: of \: both \: sides \\x = 11.62\)
using the opposite side of triangle and
\(using \: pythagoras \: theorem \\ {16}^{2} = {11.62}^{2} + {x}^{2} \\ 256 = 135.02 + {x}^{2} \\ 256 - 135.02 = {x}^{2} \\ 120.198 = {x}^{2} \\ take \: the \: roots \: of \: both \: sides \\ x = 10.96\)
therefore the length of line AC
\( = 3 + 10.96 \\ = 13.96\)
hope this helps
Please find the area of the unshaded portion in the diagram above

Answers
Answer:
148 cm²Step-by-step explanation:
find the two areas and remove the shaded one
18 * 10 - 8 * 4 (remember pemdas)
180 - 32 =
148 cm²
Functions defined by integrals, please let me know if you have any questions regarding the materials, I'd be more than happy to help. Thanks!

Answers
Given the function
\(D\left(t\right)=\frac{6t}{1+2t}\)Notice that
\(\begin{gathered} D\left(t\right)=6\left(\frac{t}{1+2t}\right)=6\left(\frac{1}{2}-\frac{1}{4t+2}\right) \\ \Rightarrow D\left(t\right)=6\left(\frac{1}{2}-\frac{1}{2\left(2t+1\right)}\right) \end{gathered}\)Then, integrate D(t) from t=0 to t=3, as shown below
\(\Rightarrow\int_0^3D\left(t\right)dt=\int_0^36\left(\frac{1}{2}-\frac{1}{2\left(2t+1\right)}\right)dt=6\left(\frac{1}{2}\int_0^3dt-\frac{1}{2}\int_0^3\frac{dt}{\left(2t+1\right)}\right?\)Then,
\(\Rightarrow\int_0^3D\left(t\right)dt=6\left(\frac{1}{2}*3-\frac{1}{2}\int_0^3\frac{dt}{2t+1}\right)\)As for the remaining integral, set x=2t+1; then dx=2dt. Solving using that substitution,
as for the integration limits, when t=3, x=7, and when t=0, x=1.
\(\int_0^3\frac{dt}{2t+1}=\frac{1}{2}\int_1^7\frac{dx}{x}=\frac{1}{2}\left(ln\left(7\right)-ln\left(1\right)\right?=\frac{1}{2}\left(ln\left(\frac{7}{1}\right)\right)=\frac{1}{2}ln\left(7\right)\)Therefore,
\(\Rightarrow\int_0^3D\left(t\right)dt=6\left(\frac{3}{2}-\frac{1}{2}\left(\frac{1}{2}ln\left(7\right)\right)\right)=9-\frac{3}{2}ln\left(7\right)\)Rounding to three decimal places,
\(\Rightarrow\int_0^3D\lparen t)dt\approx6.081\)Thus, the answer is 6.081
The graph displays the distance a CO2 car traveled in a race.
Help!!!

Answers
Answer:
5 seconds per foot
Step-by-step explanation:
Answer:A
Step-by-step explanation:
Kris currently has $190 and plans to earn more money each of the 8 weekends this summer She wants at least $1,625 by the end of the summer Write and solve an inequality for the amount of money Kris needs to earn each weekend Which answer choice best interprets the solution in the context of the problem?
A. Kris needs $179.38 more to meet her goal
B. Kris needs $13.13 each hour to meet her goal
C. Kris needs to earn at least $179.38 each weekend to meet her goal
D. Kris needs to earn $105 more to meet her goal
Answers
Kris currently has $190 and wants to have at least $1,625 by the end of the summer. To find out how much money she needs to earn each weekend we need to subtract the money she already has from the money she wants to have and divide that by the number of weekends.
$1,625 - $190 = $1,435
$1,435 ÷ 8 = $179.38
So, Kris needs to earn at least $179.38 each weekend to reach her goal.
Answer choice C. Kris needs to earn at least $179.38 each weekend to meet her goal. is the best interpretation of the solution in the context of the problem.
5 and (-5) are 0 pair
Answers
Answer:
Yes they are a 0 pair
Step-by-step explanation:
5+(-5)=0
5-5=0
Find each product. Then determine which conclusion can be drawn based on the results.
√2•√2
√5•√7
√ 2•18
√2•√6
The product of two irrational numbers is always rational.
The product of two irrational numbers can be rational or irrational.
The product of two irrational numbers is always irrational.
The product of two irrational numbers cannot be determined.
Answers
Answer:
Second answer:
"The product of two irrational numbers can be rational or irrational"
Step-by-step explanation:
notice from the first product
\(\sqrt{2} \,* \,\sqrt{2} = \sqrt{4} = 2\)
that the product of two irrational numbers can give us a rational one.
from the other three examples, the answer for the products always contains a square root that cannot be reduced, so they all result in an irrational number.
Then, depending on the type of irrationals used, the product can be either rational or irrational.
2.6x0.47pls help
pls pls
Answers
Answer:
1.222
Step-by-step explanation:
I’m am really confused on this question

Answers
Answer:
2x^7
Step-by-step explanation:
add the exponents because they both are x
2x^4*x^3=2x^7
Mitchell plans to use ASA to prove that two triangles made from a rectangular piece of wood are the same. Which diagram would support his plan to use ASA?
Answers
The solution is given below.
What is triangle?A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted \triangle ABC. In Euclidean geometry, any three points, when non-collinear, determine a unique triangle and simultaneously, a unique plane.
here, we have,
Remember that the Angle-Side-Angle Postulate (ASA) states that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.
According to this, the correct answer is: given below.
To learn more on triangle click:
brainly.com/question/29126067
#SPJ1

Which functions have a maximum and are transformed to the left and down of the parent function, f(x)=x2? Check
all that apply.
p(x) = 14(x + 7)² + 1
g(x) = -5(x + 10)² - 1
s(x) = –(x − 1)? +0.5
g(x) = 2x² + 10x-35
t(x) = -2x² - 4x - 3
Answers
Using translation concepts, the functions that have a maximum and are transformed to the left and down of the parent function are given by:
g(x) = -5(x + 10)² - 1t(x) = -2x² - 4x - 3What is a translation?A translation is represented by a change in the function graph, according to operations such as multiplication or sum/subtraction in it's definition.
For the translations, we have that:
Shift left, hence x -> x + a, a > 0.Shift down, hence y -> y - a, a > 0.Having a maximum means that the leading coefficient is negative.The functions that respect these conditions are:
g(x) = -5(x + 10)² - 1t(x) = -2x² - 4x - 3 = -2(x² + 2x) - 3 = -2(x + 1)² - 1More can be learned about translation concepts at https://brainly.com/question/4521517
#SPJ1
a data collected by a final year statistics students shows that , of the 120 cars which took the road worthiness test at DVLA office in kumasi in june 2023, only 60% passed .Among those who failed due to faults in brakes, light and steering occured as follows : brake only 14, brakes and steering 7, brake and light 10, steering and light only 3, brakes , steering and light 4. Both the number of cars that failed due to fault in steering only is the same as those that failed due to faults in light only. i. how many cars had faulty light ii. find the number of cars which had only one fault iii. find the number of cars which had at least two fault iv. find the number of cars which had fault in brake or light but not steering
Answers
According to given data collection, the answers are as follows: 17 cars had faulty light, 34 cars had only one fault, 11 cars had at least two faults and 41 cars had a fault in brake or light but not steering.
What is data collection?
Data collection is the process of gathering and measuring information or data on variables of interest, in an established systematic fashion that enables one to answer queries, stated research questions, test hypotheses, and evaluate outcomes.
i. To find the number of cars that had faulty light, we need to add up the number of cars that failed with faults in light: brake and light, steering and light only, and brakes, steering, and light. So, 10 + 3 + 4 = 17 cars had faulty light.
ii. To find the number of cars that had only one fault, we need to add up the number of cars that failed with only brake, only steering, or only light faults. So, 14 + 3 + 17 = 34 cars had only one fault.
iii. To find the number of cars that had at least two faults, we need to add up the number of cars that failed with 2 or 3 faults. So, 7 + 4 = 11 cars had at least two faults.
iv. To find the number of cars that had a fault in brake or light but not steering, we need to add up the number of cars that failed with only brake or light faults. So, 14 + 10 + 17 = 41 cars had a fault in brake or light but not steering.
Therefore, according to given data collection, the answers are as follows: 17 cars had faulty light, 34 cars had only one fault, 11 cars had at least two faults and 41 cars had a fault in brake or light but not steering.
To learn more about data collection visit:
https://brainly.com/question/29441681
#SPJ1
dividing 1/9 is equal to multiplying by
Answers
Answer: 9
Step-by-step explanation: To divide we need to flip the second fraction we are dividing by. For example:
10/1 divided by 1/4 = 10/1 times 4/1. So in this case, the answer is 40.
Now lets try it with 1/9.
X divided by 1/9 = X times 9/1.
So dividing by 1/9 is equal to multiplying by 9.
Find two z values, one positive and one negative, that are equidistant from the mean SO that the areas in the two tails add to 5% A) z =+1,96 and z = -1,96 B) 2 =+0.13andz =-0.13 2= +1.65 and 2 =-1.65 D) z = +2.58 and z =-2.58
Answers
The two z values are -1.96 and +1.96 this means that option A is the correct choice.
From the given information we know that P(-z<Z or Z>z) = 5% = 0.05.
Then the table (area under the normal curve) the probability of values smaller than a certain z-score of the standard normal distribution.
Now the standard normal distribution is symmetric about 0.
P(-z<Z)=P(-z<Z or Z>z)/2
P(-z<Z)=0.05/2
P(-z<Z)=0.025
Here we have to determine the corresponding z-score in area under the normal curve table.
The corresponding z-score z is then given in row/column title of area under the normal curve table which corresponding to a probability of 0.025 or the probability closest.
-z = -1.96
Two z -values , positive and negative that are equidistance from the mean so that the area in two tailed total 5% are,
= ±1.967 = ±1.96
z=-1.96,+1.96
Therefore, the correct option is A.
To learn more about standard normal distribution check the link below:
https://brainly.com/question/26822684
#SPJ4
for each of the number lines, write an absolute value equation in the form |x-c|=d, where c and d are some numbers, to satisfy the given solution set.

Answers
An absolute value is the numerical value of a number without consideration of its sign. It can be represented graphically by a straight line known as a number line. Absolute value equations are equations that include absolute values of variables or unknown quantities. The following are examples of how to write an absolute value equation in the form |x-c|=d to fit the provided solution sets:
Example 1:
Solution set: {x|x≤-3 or x≥1}
Absolute value equation: |x-(-1)|=4
Explanation: -1 is the midpoint of the two ranges (-3 and 1) in the solution set. |x-(-1)|=|x+1| is the absolute value expression for the midpoint -1. The distance d from -1 to the solutions' furthest endpoints, 1 and -3, is four, hence the value of d in the absolute value equation is 4.
For such more question on equations
https://brainly.com/question/22688504
#SPJ11
Which equation describes the graph? y = |x – 2| + 1
y = |x + 1| + 2
y = |x – 1| + 2
y = |x + 2| + 1
Answers
An equation that describes the graph include the following: C. y = |x – 1| + 2.
What is a translation?In Mathematics and Geometry, the translation of a graph to the right simply means adding a digit to the numerical value on the x-coordinate of the pre-image while the translation of a graph upward simply means adding a digit to the numerical value on the y-coordinate (y-axis) of the pre-image.
Since the parent function is f(x) = |x|, g(x) or y would be created by translating f(x) one (1) unit to the right and two units upward as follows;
f(x) = |x|
g(x) = f(x - 1) + 2
y = |x – 1| + 2
Read more on function and translation here: brainly.com/question/31559256
#SPJ1
Missing information:
The question is incomplete and the complete question is shown in the attached picture.

A red purse contains $7, and a black purse contains $10. Each package contains X red purses and Y black purses. If there are N packages (N ≥ 2) and the total value of them is $2021 and if each of X, Y, and N are positive integers, what is X+Y+N?
Answers
If each of X, Y, and N are positive integers, then the value of X+Y+N is 212.1
What are system of inequalities?A collection of inequalities for which we consider common solution for all inequalities is called a system of inequalities.
WE are given that A red purse contains $7, and a black purse contains $10. Each package contains X red purses and Y black purses.
X = 7
Y = 10
If there are N packages (N ≥ 2) and the total value of them is $2021
X + Y = One packages
N packages = N(X + Y ) = 10 N
if each of X, Y, and N are positive integers, then;
10 N = 2021
N = 2021/10
N = 202.1
Therefore, X+Y+N = 10 + 202.1 = 212.1
Learn more about solutions to the system of inequalities here:
https://brainly.com/question/16339562
#SPJ1
Consider the figure below and answer the questions that follows. Please help me prepare for my finals!!!!

Answers
Using the distance formula, the length of segment PQ is:
C. √68 units
How to Find the Length of a Segment Using the Distance Formula?The distance formula is given as:
d = \(\sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\).
Segment PQ has the following endpoints:
P(-2, 3)
Q(6, 1)
To find the length of segment PQ using the distance formula, we can apply the formula, where:
\((x_1, y_1)\)are the coordinates of point P
\((x_2, y_2)\) are the coordinates of point Q.
Given:
P(-2, 3) = \((x_1, y_1)\)
Q(6, 1) = \((x_2, y_2)\)
Let's substitute the values into the formula:
PQ = √[(6 - (-2))² + (1 - 3)²]
PQ = √[(8)² + (-2)²)
PQ = √(64 + 4)
length of segment PQ = √68 units
Learn more about length of segment on:
https://brainly.com/question/24778489
#SPJ1
please help i just need to get this done.

Answers
The equation of the line in slope-point form, slope-intercept form, and standard form are y = -100x + 1250, y - 1250 = -100(x-0) and 100x + y = 1250 respectively
How to write the equation of a line in point-slope form?
The equation of a line in point-slope form is given as y − y 1 = m ( x − x 1),
where ( x 1, y1 ) is the point given and m is the slope
m = y2-y1 / x2-x1, where x1 = 0, y1 = 1,250 and x2 = 5, y2 = 750
m = 750-1250 / 5-0
m = -500/5 = -100
Thus, the slope-point form:
y − y 1 = m ( x − x 1 )
y - 1250 = -100(x-0)
The equation of a line in slope-intercept form is given as y = mx+c,
where (x, y) is the point given, m is the slope and c is the y-intercept
where x1 = 0, y1 = 1,250 and m = -100
y = mx + c
1250 = -100(0) + c
c = 1250
Thus, the equation in slope-intercept form is:
y = -100x + 1250
The equation of a line in standard form is given as ax + by = c, where a, b, c are real numbers
Rewrite y = -100x + 1250. Thus, the equation in standard form is:
100x + y = 1250
Learn more about equation of a line on:
https://brainly.com/question/13763238
#SPJ1
Plz help. I dont know how to solve this plz.

Answers
Answer:
its 0,6
Step-by-step explanation:
you just move however much it asks
Answer:
(0,6)
Step-by-step explanation:
your basically imagining that your moving that point following the directions in the word problem. go left 3 times, go up 2 times.
The circumference of a circle is 11 π ft. Find its diameter, in feet.
Answers
The diameter of the circle when the circumference is 11 π ft will be 11 feet.
What is the circumference of a circle?A circle's circumference is defined as the linear distance around its boundary, or if a circle is opened to form a straight line.
The formula for the circumference of a circle is:
C = πd
where C is the circumference and d is the diameter.
We are given that the circumference of the circle is 11π ft, so we can set up an equation:
11π = πd
Simplifying by dividing both sides by π:
11 = d
Therefore, the diameter of the circle is 11 feet.
To know more about the circumference of a circle follow
https://brainly.com/question/23986334
#SPJ1
A television selling for $940.00 is marked down by 15%. What is the price after the markdown?
Answers
Step-by-step explanation:
100%-> 940.00
100%-15%=85%
85%->940.00 ÷ 100 x 85
=799. 00