Suppose $a$, $b$ and $c$ are integers such that the greatest common divisor of $x^2 ax b$ and $x^2 bx c$ is $x 1$ (in the set of polynomials in $x$ with integer coefficients), and the least common multiple of $x^2 ax b$ and $x^2 bx c$ is $x^3-4x^2 x 6$. Find $a b c$.
Answers
The GCD is \(x+1\), so \(x+1\) divides both \(x^2+ax+b\) and \(x^2+bx+c\). For some \(\alpha\) and \(\beta\) we can write
\(x^2 + ax + b = (x + 1) (x - \alpha)\)
\(x^2 + bx + c = (x + 1) (x - \beta)\)
Expanding the right sides, we get
\(x^2 + ax + b = x^2 + (1 - \alpha) x - \alpha\)
\(x^2 + bx + c = x^2 + (1 - \beta) x - \beta\)
\(x+1\) also divides the LCM, so
\(x^3 - 4x^2 + x + 6 = (x + 1) (x - \alpha) (x - \beta)\)
and expanding gives
\(x^3 - 4x^2 + x + 6 = x^3 + (1 - \alpha - \beta) x^2 + (\alpha \beta - \alpha - \beta) x + \alpha \beta\)
Matching up all the coefficients, we have
\(\begin{cases} a = 1 - \alpha \\ b = -\alpha \\ b = 1 - \beta \\ c = -\beta \\ -4 = 1 - \alpha - \beta \\ 1 = \alpha \beta - \alpha - \beta \\ 6 = \alpha \beta \end{cases} \implies \alpha + \beta = 5\)
All the unknowns are integers, and we have the prime factorization 6 = 2×3 that also satisfies 5 = 2 + 3.
• If \(\alpha=2\) and \(\beta=3\), then \(a=-1\), \(b=-2\), and \(c=-3\).
• If \(\alpha=3\) and \(\beta=2\), then there is no solution for \(a,b,c\) since
\(\begin{cases}b = -\alpha \\ b = 1-\beta \end{cases} \implies \alpha = \beta - 1\)
but 3 ≠ 2 - 1 = 1.
It follows that \(a + b + c = -1 - 2 - 3 = \boxed{-6}\).
Related Questions
PLEASE HELP ITS URGENT!!

Answers
Answer:
answer is D from what I got
in a large population, 68 % of the people have been vaccinated. if 3 people are randomly selected, what is the probability that at least one of them has been vaccinated?
Answers
in a large population, 68 % of the people have been vaccinated. if 3 people are randomly selected, 0.968 is the probability that at least one of them has been vaccinated.
What is probability?A probability is a number that expresses the possibility or likelihood that a specific event will take place. In addition to being represented as percentages ranging from 0% to 100%, probabilities can also be expressed as proportions between 0 and 1.
The probability is a measure of how likely an event is to occur. It gauges the event's degree of certainty. P(E) = Number of Favorable Outcomes/Number of All Outcomes is the formula for probability.
Given that,
In a large population, 68% of the people have been vaccinated.
Among them 3 people are randomly selected.
probability that at least one of them is vaccinated:
= 1 - P (none of the 3 has been vaccinated)
= 1 - (1 - 0.68)³
=0.968
To know more about probability refer to:
https://brainly.com/question/13604758
#SPJ4
Lonnie is an architect, who must add a new building on an already crowded college campus. To generate the most original solution to this problem, he will most likely
Answers
To generate the most original solution to the problem of adding a new building on an already crowded college campus, Lonnie can employ various techniques and strategies that are often used in the field of architecture and design.
Lonnie could take:
Research and Analysis:
Before developing a design solution, Lonnie can research and analyze the existing campus architecture and the surrounding environment.
By understanding the context, Lonnie can identify potential constraints, opportunities, and design challenges, which can inform his design decisions.
Creative Brainstorming:
Lonnie can brainstorm and generate a wide range of design ideas, without censoring or judging them.
This can be done individually or in a group, using various brainstorming techniques such as mind mapping, word association, or random stimulus.
Sketching and Modeling:
Lonnie can explore and refine his design ideas by sketching and modeling them in two- or three-dimensions.
This can help him visualize the design in different scales and perspectives, and experiment with different materials, textures, and colors.
Prototyping and Testing:
Lonnie can create physical or digital prototypes of the design to test its feasibility, functionality, and aesthetic qualities.
This can involve building mock-ups, conducting simulations, or using virtual reality tools.
Cross-Disciplinary Collaboration:
Lonnie can collaborate with experts from different fields, such as engineering, sustainability, psychology, or sociology, to incorporate their knowledge and perspectives into the design process.
This can help Lonnie generate innovative and holistic solutions that address multiple needs and values.
Lonnie can generate original and effective design solutions that meet the needs and aspirations of the campus community.
For similar questions on Architecture
https://brainly.com/question/16135742
#SPJ11
Q1-) Consider a manufacturing system with two machines. Suppose that when both ma- chines are available, one is in use and the other is on standby. The probability that a machine in use fails during a day is p. When it fails its repair may start only the next day if the single repair facility is available. It takes two days to repair a failed machine. We can use a Markov Chain model to describe the evolution of this system. Let Xn = (i, j), n ≥ 0 denote the states of the Markov chain, where i is the number of machines in working condition and j is the number of elapsed repair days of a machine at the repair facility at the beginning of the n'th day. The corresponding transition probability matrix is (2,0) (1,0) (1,1) (0,1) (2,0) [1-p P 0 0 (1,0) 0 0 1-p Р P= (1,1) 1-p 0 0 P (0,1) 0 1 0 0 For parts (a)-(c) do not assume a specific value for p, leave your answer in terms of p. (a) Given Xo = (1, 1), what is the probability that only one machine is in working condition after two days? (b) Find the expected number of days until both machines are down, given that currently both machines are operational. (c) Find the steady state probabilities. (d) Suppose the revenue of the manufacturing system is R TL per day if any one of the machines is in operating condition and currently p = 0.3. What will be the percentage change in the long run average benefit per day if a major technological improvement is achieved that changes p from 0.3 to 0.2?
Answers
(a) To find the probability that only one machine is in working condition after two days, we need to determine the probability of transitioning from state (1, 1) to state (1, 0) after two days.
From the transition probability matrix, we see that to transition from (1, 1) to (1, 0) in one day, both machines need to remain operational, which has a probability of (1 - p) * (1 - p) = (1 - p)^2.
Therefore, the probability of transitioning from (1, 1) to (1, 0) after two days is ((1 - p) * (1 - p))^2 = (1 - p)^4.
(b) To find the expected number of days until both machines are down, given that currently both machines are operational, we need to consider the transition probabilities from state (2, 0) to state (0, 1).
From the transition probability matrix, we see that to transition from (2, 0) to (0, 1) in one day, both machines need to fail, which has a probability of p * p = p^2.
Therefore, the expected number of days until both machines are down, given that both machines are currently operational, is 1 / (p^2).
(c) To find the steady-state probabilities, we need to solve the equation πP = π, where π is the row vector of steady-state probabilities and P is the transition probability matrix.
Solving this equation will give us the steady-state probabilities for each state (i, j). Since the given matrix is not provided, it is not possible to calculate the exact steady-state probabilities without the specific values of the transition probabilities.
(d) To determine the percentage change in the long-run average benefit per day if p changes from 0.3 to 0.2, we would need to know how the revenue R TL is related to the probability p. Without this information, it is not possible to calculate the percentage change.
To learn more about probability : brainly.com/question/31828911
#SPJ11
evaluate dw/dt at t = 4 for the function w (x,y)= e^y - ln x; x = t^2, y = ln t
Answers
dw/dt at t = 4 = -2/4 + 4 = 3
We can use the chain rule to find dw/dt:
dw/dt = (∂w/∂x) (dx/dt) + (∂w/∂y) (dy/dt)
First, we need to find ∂w/∂x and ∂w/∂y:
∂w/∂x = -1/x
∂w/∂y = e^y
Next, we can substitute x = t^2 and y = ln t into these expressions:
∂w/∂x = -1/(t^2)
∂w/∂y = e^(ln t) = t
We also have dx/dt = 2t and dy/dt = 1/t. Substituting all these values into the formula for dw/dt, we get:
dw/dt = (∂w/∂x) (dx/dt) + (∂w/∂y) (dy/dt)
= (-1/(t^2)) (2t) + (t) (1/t)
= -2/t + t
Finally, we can evaluate dw/dt at t = 4:
dw/dt = -2/t + t
dw/dt at t = 4 = -2/4 + 4 = 3
To know more about chain rule refer here:
https://brainly.com/question/28972262
#SPJ11
Need help can’t find answer anywhere

Answers
Both the angles can be equated because they are alternate interior angle.
Hence,
3x = 2x + 20
→ 3x - 2x = 20
→ x = 20
helpppppppppppp btw not a test

Answers
Answer:
2.1
Step-by-step explanation:
Find the surface area of the composite figure. Round your answer to the nearest tenth if necessary.

Answers
If the length,breadth, height of cuboid are 16 m, 5 m,4 m , slant height of pyramid is 10m, height be 6 m then the surface area of composite figure be 444 \(m^{2}\).
Given that the length,breadth,height of cuboid are 16m,5 m, 4m and slant height be 10 m and height be 6 m.
Surface area is basically sum of area of all the sides of a figure.
Surface area of composite figure = area of cuboid less area of common side + area of 2 slant sides of pyramid+area of two triangles.
=2(lb+bh+hl)-(lb)+2(slant height*breadth of cuboid)+2[1/2* length of cuboid* height of triangle)
=2(16*5+5*4+4*16)-16*5+2(10*5)+2[1/2*16*6]
=2(80+20+64)-80+2*50+2(48)
=2(164)-80+100+96
=328-80+196
=248+196
=444\(m^{2}\)
Hence the surface area of composite figure having a cuboid and pyramid on top is 444\(m^{2}\).
Learn more about surface area at https://brainly.com/question/1297098
#SPJ1
36. What is the value of f(3) if f(x) = -4x + 2?
F -14
G-10
H-6
J 14
Answers
Answer:
G-10
Step-by-step explanation:
because i dont have time to expalin
Let R be the region in the first quadrant lying outside the circle r=87 and inside the cardioid r=87(1+cos 6). Evaluate SI sin e da. R
Answers
To evaluate ∬ᵣ sin(θ) dA over region R, where R is the region in the first quadrant lying outside the circle r = 87 and inside the cardioid r = 87(1 + cos(6θ)): the answer is 0.
The given region R lies between two curves: the circle r = 87 and the cardioid r = 87(1 + cos(6θ)). The region is bounded by the x-axis and the positive y-axis.
Since the region lies outside the circle and inside the cardioid, there is no overlap between the two curves. Therefore, the region R is empty, resulting in an area of zero.
Since the integral of sin(θ) over an empty region is zero, the value of ∬ᵣ sin(θ) dA is 0.
Hence, the main answer is 0.
learn more about cardioid here:
https://brainly.com/question/32730534
#SPJ11
6x-3=3x+12 what is the solution to the equation?
Answers
Answer:
x=5
Step-by-step explanation:
add 3 to both sides of the equation: -3+3=0 12+3=15 simplified: 6x=3x+15 then subtract 3x from both sides of the equation. simplified: 3x=15
then divide both sides by 3. simplified: x=5
If AB=6 A B = 6 and BC=11 B C = 11 ,what is the length of AC A C ?
Answers
The length of the third side can be in range of [1, 17].
What are triangles?A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. In Euclidean geometry, any three points, when non-collinear, determine a unique triangle and simultaneously, a unique plane
Given is that in triangle ABC, AB = 6 and BC = 11.
In a triangle, the sum of two sides of a triangle is always greater than the third side. This means -
AB + BC > AC
(6 + 11) > AC
AC < 17
Therefore, the length of the third side can be in range of [1, 17].
To solve more questions on triangles, visit the link below -
brainly.com/question/12413243
#SPJ1
The equations 9 x minus 10 y = 6, 8 x minus 10 y = negative 23, 9 x + 10 y = negative 16, and 8 x + 10 y = 13 are shown on the graph below. On a coordinate plane, there are 4 lines. Green line goes through (negative 2, 0.75) and (negative 2, 1.5). Blue line goes through (negative 1.75, 0) and (1, negative 2). Pink line goes through (negative 1.5, negative 2), and (1.5, 0.75). Purple line goes through (0, 1.25) and (1, 0.5). PLEASE ANSWER IS 2 MINUTES WILL GIVE BRAINLIEST Which is the approximate solution for the system of equations 8 x minus 10 y = negative 23 and 9 x + 10 y = negative 16? (–2.3, 0.5) (–2.5, 1) (–2.3, –0.5) (–2.5, –1)
Answers
Answer:
Step-by-step explanation:
The two equations are 8x-10y=-23 and 9x+10y=-16.
If you plug them both into a graphing calculator, you will see that the point where they cross (the solution) is (-2.3, 0.5).
The answer is A.
Answer:
i think it is A
Step-by-step explanation:
if right pls give brainliest
Nvm it is right pls give brainliest i need 5 to get to next rank
An international fast food chain is looking at opening a new franchise in Emerald, Queensland. They contact a marketing research firm to help them assess the level of interest in the restaurant within the town. From a list of all the residential addresses in Emerald, the firm selects a simple random sample of 100 and mails a brief questionnaire to each. The population of interest is
Select one:
a. all people in Emerald, Queensland.
b. all adults in Emerald, Queensland.
c. the 100 addresses to which the questionnaire was mailed.
d. the people in Emerald who eat fast food.
e. all residential addresses in Emerald, Queensland.
Answers
The population of interest is: A. all people in Emerald, Queensland.
The population of interest refers to the group of individuals that the research is trying to draw inferences about. In this case, the international fast food chain is looking to assess the level of interest in opening a franchise in Emerald, Queensland.
Therefore, the population of interest is all people who live in Emerald, Queensland, as they are the group that the research is trying to understand. The sample of 100 addresses that the research firm selected is just a subset of this population and the questionnaires are being sent to them to infer about the entire population.
To know more ablout food chain click on below link:
https://brainly.com/question/16065961#
#SPJ4
The difference of x and y is 14. The value of x is 3 more than
twice the value of y. Write two equations and graph to find
the value of x.
O X = 25
O x = -17
OX= 4
O x = 11
Answers
The value of X = 25.
The difference of x and y is 14. The value of x is 3 more thantwice the value of y. Find the value of x and y.Solution:
The two equations are
(i) the first condition is difference of x and y is 14
x - y = 14 ---------equation 1
(ii) the second condition of the given data is value of x is 3 times more than two times of y value.
x - 2y = 3 --------equation 2
From equation 2, we have to separate two variables x and y,
x = 3 + 2y --------equation 3
We have to Substitute equation 3 in equation 1
3 + 2y - y = 14
3 + y = 14
y = 14 - 3
y = 11
Substitute y = 11 in equation 1........
x - 11 = 14
x = 14 + 11
x = 25
So, the value of x is 25 and y is 11.
To learn more about equations refer to:
https://brainly.com/question/2972832
#SPJ1
Answer:
x - y = 14x - 2y = 3x = 25Step-by-step explanation:
Given the difference of x and y is 14, and the difference of x and 2y is 3, you want two equations, their graph, and the value of x.
EquationsThe difference of 'a' and 'b' is (a -b). Here, the two differences are expressed as the equations ...
x - y = 14x - 2y = 3GraphThe attachment shows a graph of these equations. Their point of intersection is (25, 11), meaning the value of x is 25.
The graph of the first equation is easily drawn by recognizing the x- and y-intercepts are 14 and -14, respectively.
The graph of the second equation will go through the x-intercept point of (3, 0) and the y-intercept point of (0, -3/2). It is probably easier to graph this by hand by considering the x-intercept point and the slope of 1/2.
Algebraic solutionSince we're only interested in the value of x, it is convenient to eliminate the variable y. We can to that by subtracting the second equation from twice the first:
2(x -y) -(x -2y) = 2(14) -(3)
x = 25 . . . . . . . . . simplify

Find the sum. 12.9 + 4.5 + 3.66
Answers
Answer:
21.06
Step-by-step explanation:
the answer is 21.06
hope this helped!
Please help. Don’t answer if you don’t know. Your waisting my points when you do so. I need it to be right also. Thanks-
Answers
Answer:
what? answers I can see it
Step-by-step explanation:
please check before you message
PLSSS HELP IF YOU TURLY KNOW THISS

Answers
Answer:
3 1/2
Step-by-step explanation:
the letter j is HALFway between four and three so it is 3 1/2
Someone please help me

Answers
Answer:
m∠B ≈ 28.05°
Step-by-step explanation:
Because we don't know whether this is a right triangle, we'll need to use the Law of Sines to find the measure of angle B (aka m∠B).
The Law of Sines relates a triangle's side lengths and the sines of its angles and is given by the following:
\(\frac{sin(A)}{a} =\frac{sin(B)}{b} =\frac{sin(C)}{c}\).
Thus, we can plug in 36 for C, 15 for c, and 12 for b to find the measure of angle B:
Step 1: Plug in values and simplify:
sin(36) / 15 = sin(B) / 12
0.0391856835 = sin(B) / 12
Step 2: Multiply both sides by 12:
(0.0391856835) = sin(B) / 12) * 12
0.4702282018 = sin(B)
Step 3: Take the inverse sine of 0.4702282018 to find the measure of angle B:
sin^-1 (0.4702282018) = B
28.04911063
28.05 = B
Thus, the measure of is approximately 28.05° (if you want or need to round more or less, feel free to).
which is the completely factored form of 12x^3-60x^2+4x-20
Answers
Answer:
4(x-5)(3x² +1)
Step-by-step:
Add and subtract the second term to the expression and factor by grouping.
Hope this helps!
Which line is a line of symmetry for the figure below?
A.
Line A
B.
Line C
C.
Line D
D.
Line B

Answers
Answer:
A.
Line A
Please mark my answer the brainliestIn the figure b and c are parallel lines select all the statements that are true

Answers
Did you ever get the answer
Answer:
Im the king of answers
Step-by-step explanation:
The answer is A, C, and E
3. What is the surface area of this composite solid? Show your work.
5 ft
5 ft
3 ft
4 ft
10 ft
8 ft
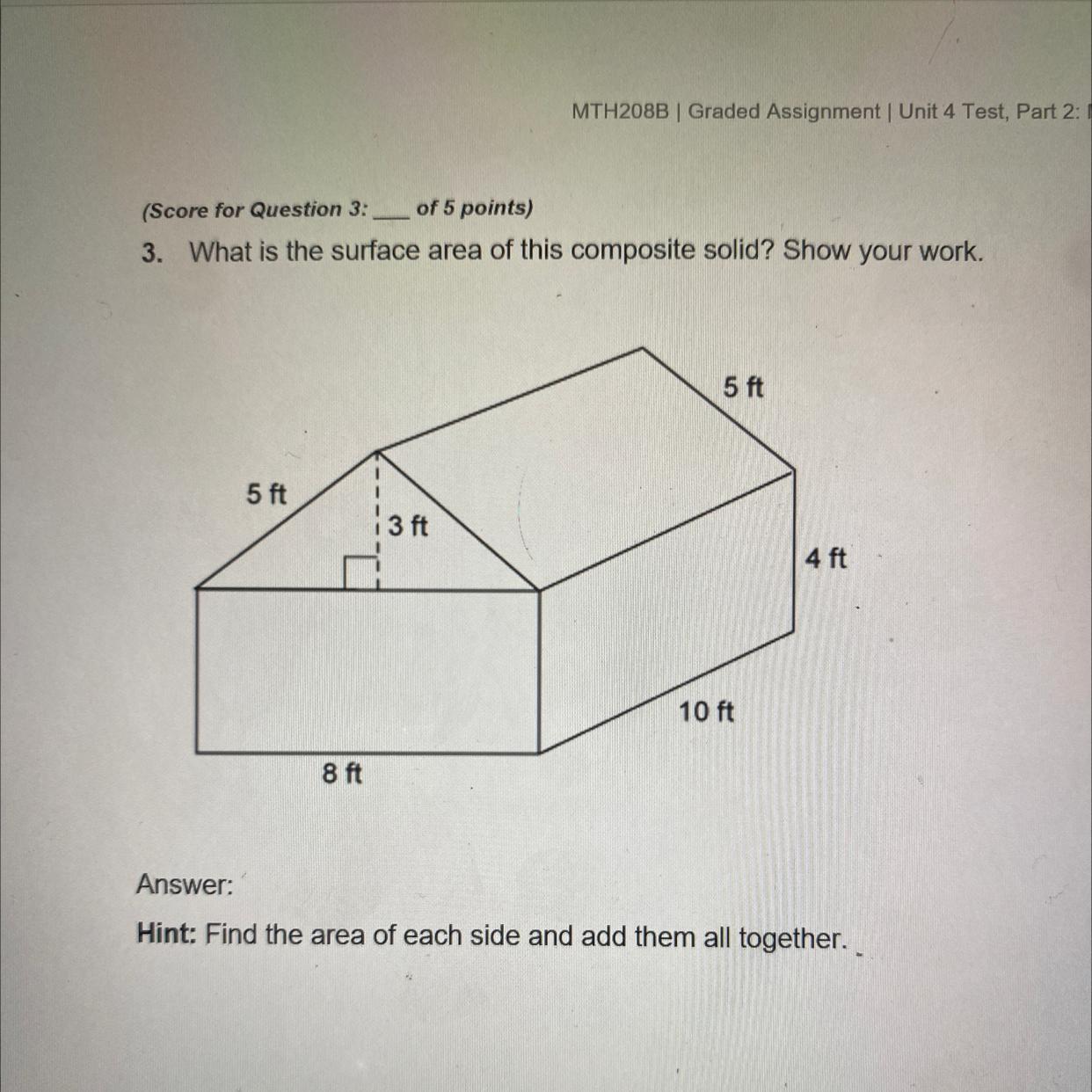
Answers
By finding the area of the simpler parts, we will see that the total surface area of the figure is 348 ft^2
How we do get the surface area?
We can divide this in smaller parts. First, remember that for a triangle of base b and height h, the area is:
A = b*h/2
Then for each of the triangles in the image, the area is:
A = 8ft*3ft/2 = 12 ft^2
And we have two of these.
Then we have the base, a rectangle of 8ft by 10ft, with an area:
A' = 8ft*10ft = 80ft^2
Then we have the front and back sides, rectangles of 8ft by 4ft, with an area:
A'' = 8ft*4ft = 32 ft^2 (we have two of these).
Then the lateral sides, rectangles of 10ft by 4ft, with an area:
A''' = 10ft*4ft = 40ft^2 (we have two of these)
Finally, we have the top rectangles, of 5ft by 10ft, each with an area:
A'''' = 5ft*10ft = 50ft^2 (we have two of these).
Adding all the areas, we get:
Area = 2*(12 ft^2 + 32 ft^2 + 40ft^2 + 50ft^2) + 80ft^2 = 348 ft^2
If you want to learn more about areas, you can read:
https://brainly.com/question/24487155
Bill’s FICA tax is 7.65% of his earnings of 325.78 per week. How much FICA tax should his employer withhold?
A. $27.92
B.$26.42
C. $25.28
D. $24.92
Answers
The employer of Bill’s FICA should withhold D. $24.92 in taxes
What is a percentage?Percentage is defined as the number that represents a ratio of a total that is divided by 100 equal parts. It is represented by the symbol %.
To solve this exercise, the percentage formula and the procedure to be applied is as follows:
n= (% * nt) / 100
Where:
% = percentagen= number portionnt = total of the number portionInformation about the problem:
% = 7.65%nt = $325.78n = ?Using the percentage formulate, we get how much FICA tax should his employer withhold:
n= (% * nt) / 100
n = (7.65 * $325.78)/100
n = $2492.22/100
n = $24.92
Learn more about percentage at: brainly.com/question/24877689
#SPJ4
find thevsurface area of a square pyramid wuth side length 3 km and slant height 5 km

Answers
The Total Surface Area = 4 triangles + 1 square
The TSA of the Pyramid = 4(1/2 bh) + LxL
\(\begin{gathered} d^2=3^2+3^2 \\ d^2=9+9 \\ d=\sqrt[]{18}\text{ =}\sqrt[]{9\times2}=\sqrt[]{9}\text{ }\times\sqrt[]{2}\text{ =3 }\sqrt[]{2} \end{gathered}\)\(\begin{gathered} 5^2=h^2+(\frac{3}{2})^2 \\ 25-\frac{9}{4}=h^2 \\ 25-2.25=h^2 \\ h=\sqrt[]{22.5}\text{ =1.5km} \end{gathered}\)TSA of the pyramid =
\(4(\frac{1}{2}\times5\times3)+(3^2)=(2\times15)+9=30+9=39km^2\)
Which relationship would form a graph that is not a straight line?

Answers
Answer:
D
Step-by-step explanation:
The last line is not a straight line because when you start from 1 and plug higher numbers, you see that forms a quadratic curve or parabola.
a container full of vegetable oil is slowly leaking at a constant rate. after hours, liters of oil remained in the container. after hours, liters of oil remained in the container. let represent the remaining amount of oil in the container and let represent the elapsed time (in hours). write a linear equation to estimate the remaining amount of oil based on the elapsed time. express numbers as decimals or integers.
Answers
For every hour that passes, the container loses 1.5 liters of oil.
To write a linear equation to estimate the remaining amount of oil based on the elapsed time, we can use the slope-intercept form of a linear equation, y = mx + b, where y represents the remaining amount of oil, x represents the elapsed time, m represents the slope of the line, and b represents the y-intercept.
Since the container is leaking at a constant rate, we can assume that the slope of the line is constant. We can find the slope by using the formula:
m = (y2 - y1) / (x2 - x1)
where (x1, y1) represents the first data point (hours, liters of oil), and (x2, y2) represents the second data point.
Using the given data, we have:
m = (y2 - y1) / (x2 - x1)
m = (4.5 - 6) / (2 - 1)
m = -1.5
This means that for every hour that passes, the container loses 1.5 liters of oil.
To find the y-intercept, we can use one of the data points and solve for b:
y = mx + b
6 = (-1.5)(1) + b
b = 7.5
This means that at time zero (when no time has elapsed), there are 7.5 liters of oil remaining in the container.
Therefore, the linear equation to estimate the remaining amount of oil based on the elapsed time is:
y = -1.5x + 7.5
This equation tells us that as time passes, the amount of oil in the container decreases at a constant rate of 1.5 liters per hour. The y-intercept of 7.5 represents the initial amount of oil in the container before any time has elapsed.
Learn more about equation brainly.com/question/10413253
#SPJ11
a shape has 4 sides and exactly 1 pair of parallel sides, what is best name for this shape
Answers
Answer:
This shape would be a trapezoid :)
Step-by-step explanation:
complex numbers are represented on a cartesian coordinate system with a horizontal real axis and a vertical ___ axis.
Answers
Answer: imaginary axis
Step-by-step explanation:
The first approximation of 537 can be written a b' where the greatest common divisor of a and bis 1, with a= type your answer... b = = type your answer...
Answers
The first approximation of 537 can be written as a = 536 and b = 1, where the greatest common divisor of a and b is 1.
In number theory, the greatest common divisor (GCD) of two numbers is the largest positive integer that divides both numbers without leaving a remainder. In this case, since a = 536 and b = 1, the GCD of a and b is 1. This means that 536 and 1 have no common factors other than 1.
The first approximation of 537 can be expressed as a product of these two numbers, a and b, where a represents the larger part of the approximation and b represents the smaller part. In this case, a is equal to 536, and b is equal to 1. Since the GCD of a and b is 1, it indicates that 536 and 1 have no common factors other than 1. This approximation may not be the most accurate, but it satisfies the condition of having a GCD of 1.
Learn more about greatest common divisor :
https://brainly.com/question/23270841
#SPJ11