Sung borrowed money from his parents over the last three days. This is represented by the negative values in the table.
What is the total of the values?
What is the average of the values?
Day 1 is negative 4 dollars, day 2 is negative 2 dollars, day 3 is negative 3 dollars.

Answers
Answer:
-$9
-$3
Step-by-step explanation:
So sorry i'm late!
Answer:
I'm terrible at explaining so here's a screenshot
Step-by-step explanation:

Related Questions
struggling with these

Answers
The graphs of the quadratic expressions are added as attachment
Solving the quadratic expressions by graphFunction 5
Given that
y = -x² + 8x - 14
The graph is added as an attachment and the solution is x = 2.59 and x = 5.41
Function 6
Given that
y = 1/2x² - x - 3
The graph is added as an attachment and the solution is x = -1.65 and x = 3.65
Function 7
Given that
y > x² + 6x + 5
The graph is added as an attachment and the solution is x values between -5 and -1 (exclusive)
Function 8
Given that
y ≤ 2x² - 4
The graph is added as an attachment and the solution is x values outside -1.414 and 1.414 (inclusive)
Read more about quadratic functions at
https://brainly.com/question/25841119
#SPJ1

URGENT!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
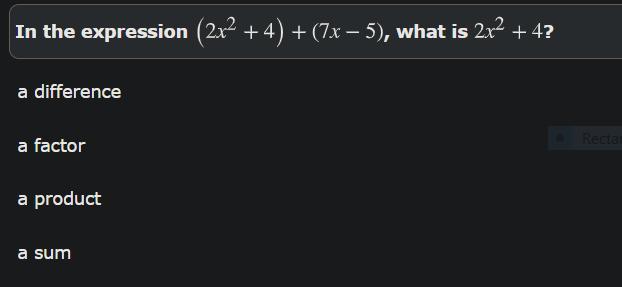
Answers
Answer:
factor I'm pretty sure sorry if I'm wrong
what's the formula of
(a+b)³ = ?
Answers
Answer:
(a+b)³=a³+3a²b+3ab²+b³
Answer:
Step-by-step explanation:
Hello!
(a+b)(a+b)(a+b)
(a+b)(a+b) = a²+2ab + b²
(a²+2ab + b²) (a+b)=
a³ + a²b + 2a²b + 2ab² + ab² + b³ =
a³ + b³ + 2a²b + 2ab² + ab² + a²b
Convert them please

Answers
Answer:
a) 1.999 moles He
b) 0.50 moles Cu
Step-by-step explanation:
Step-by-step explanation:
1 km = 1000 m = 0.621371 miles
so,
786.3 m = 0.7863 km (simply divide by 1000).
40 km/h = 40×0.621371 mph (as the reference of 1 hour stays the same).
= 24.8548 mph
always consider the direction of the conversion rate : are you going from a smaller to a larger unit, or from a larger to a smaller unit ?
if we would have said
1 m = 0.001 km
then we would have converted 786.3 m by multiplying it by 0.001 (also getting 0.7863 km as result, of course).
but because we defined it the other way around, we had to divide by 1000. it is clear that this is the same operation, yes ?
in the same way, if we would have said
1 mile = 1.60934 km
then we would have converted 40 km to miles by dividing 40 by 1.60934. again getting the same result, of course.
Bob borrowed $2,500 at an annual interest rate of 3%
Answers
Answer:
Ex:
after 7 years you will have: $3074.68
Step-by-step explanation:
$2500 × 1.037 = $2500 × 1.2299 = $3074.68
let f(p) = 15 and f(q) = 20 where p = (3, 4) and q = (3.03, 3.96). approximate the directional derivative of f at p in the direction of q.
Answers
The approximate directional derivative of f at point p in the direction of q is 0.
To approximate the directional derivative of f at point p in the direction of q, we can use the formula:
Df(p;q) ≈ ∇f(p) · u
where ∇f(p) represents the gradient of f at point p, and u is the unit vector in the direction of q.
First, let's compute the gradient ∇f(p) at point p:
∇f(p) = (∂f/∂x, ∂f/∂y)
Since f(p) = 15, the function f is constant, and the partial derivatives are both zero:
∂f/∂x = 0
∂f/∂y = 0
Therefore, ∇f(p) = (0, 0).
Next, let's calculate the unit vector u in the direction of q:
u = q - p / ||q - p||
Substituting the given values:
u = (3.03, 3.96) - (3, 4) / ||(3.03, 3.96) - (3, 4)||
Performing the calculations:
u = (0.03, -0.04) / ||(0.03, -0.04)||
To find ||(0.03, -0.04)||, we calculate the Euclidean norm (magnitude) of the vector:
||(0.03, -0.04)|| = sqrt((0.03)^2 + (-0.04)^2) = sqrt(0.0009 + 0.0016) = sqrt(0.0025) = 0.05
Therefore, the unit vector u is:
u = (0.03, -0.04) / 0.05 = (0.6, -0.8)
Finally, we can approximate the directional derivative of f at point p in the direction of q using the formula:
Df(p;q) ≈ ∇f(p) · u
Substituting the values:
Df(p;q) ≈ (0, 0) · (0.6, -0.8) = 0
Know more about directional derivative here:
https://brainly.com/question/30365299
#SPJ11
g(n) = -1 +1 n f(n) = - 1 n-1

Answers
a pipe made of metal 1cm thick , has and external radius of 11cm. find the volume of metal used in making 2.4 m long pipe
Answers
Answer:
The volume of metal used in making 2.4 m long pipe is 1.58 cm³
Step-by-step explanation:
From the question,
The external radius is 11cm.
Also, the thickness of the pipe is 1cm, then we can determine the internal radius.
Internal radius = External radius - the thickness
Internal radius = 11cm - 1cm
Internal radius = 10cm
Now, to find the volume of metal used in making the long pipe,
The volume of metal used in making the long pipe is the difference between the volume of the external cylinder and the volume of the internal cylinder.
Volume of a cylinder is given by the formula below
\(V = \pi r^{2}h\)
Where \(V\) is the volume of the cylinder
\(\pi\) is constant ( Take \(\pi\) = 3.14)
\(r\) is the radius
and \(h\) is the height
Let the radius of the external cylinder be R,
then, R = 11 cm = 0.11 m
and let the radius of the internal cylinder be r
then, r = 10 cm = 0.10 m
Then,
The volume of metal used in making the long pipe = \(\pi R^{2}h - \pi r^{2}h\)
= \(\pi (R^{2} - r^{2})h\)
= \(3.14\times(0.11^{2} - 0.10^{2})\times2.4\)
= \(3.14\times(0.0121 - 0.01)\times2.4\\\)
= \(3.14\times(0.0021 )\times2.4\\\)
= 0.0158 m³ or 1.58 cm³
Hence, the volume of metal used in making 2.4 m long pipe is 1.58 cm³
according to statista, united airlines controlled 15% of the domestic market during a recent year. a random sample of 125 domestic passengers that year was selected. using the normal approximation to the binomial distribution, what is the probability that 10 or fewer passengers from this sample were on united airlines flights? group of answer choices 0.0485 0.0192 0.2877 0.4286
Answers
Answer:
Step-by-step explanation:
Q4) Let x denote the time taken to run a road race. Suppose x is approximately normally distributed with a mean of 190 minutes and a standard deviation of 21 minutes. If one runner is selected at random, what is the probability that this runner will complete this road race: In less than 160 minutes? * 0.764 0.765 0.0764 0.0765 In 215 to 245 minutes? * 0.1128 O 0.1120 O 0.1125 0.1126
Answers
a. The probability that this runner will complete this road race: In less than 160 minutes is 0.0764. The correct answer is C.
b. The probability that this runner will complete this road race: In 215 to 245 minutes is 0.1125 The correct answer is C.
a. To find the probability for each scenario, we'll use the given normal distribution parameters:
Mean (μ) = 190 minutes
Standard Deviation (σ) = 21 minutes
Probability of completing the road race in less than 160 minutes:
To calculate this probability, we need to find the area under the normal distribution curve to the left of 160 minutes.
Using the z-score formula: z = (x - μ) / σ
z = (160 - 190) / 21
z ≈ -1.4286
We can then use a standard normal distribution table or statistical software to find the corresponding cumulative probability.
From the standard normal distribution table, the cumulative probability for z ≈ -1.4286 is approximately 0.0764.
Therefore, the probability of completing the road race in less than 160 minutes is approximately 0.0764. The correct answer is C.
b. Probability of completing the road race in 215 to 245 minutes:
To calculate this probability, we need to find the area under the normal distribution curve between 215 and 245 minutes.
First, we calculate the z-scores for each endpoint:
For 215 minutes:
z1 = (215 - 190) / 21
z1 ≈ 1.1905
For 245 minutes:
z2 = (245 - 190) / 21
z2 ≈ 2.6190
Next, we find the cumulative probabilities for each z-score.
From the standard normal distribution table:
The cumulative probability for z ≈ 1.1905 is approximately 0.8820.
The cumulative probability for z ≈ 2.6190 is approximately 0.9955.
To find the probability between these two z-scores, we subtract the cumulative probability at the lower z-score from the cumulative probability at the higher z-score:
Probability = 0.9955 - 0.8820
Probability ≈ 0.1125
Therefore, the probability of completing the road race in 215 to 245 minutes is approximately 0.1125. The correct answer is C.
Learn more about probability at https://brainly.com/question/32274851
#SPJ11
Admission to the Chesterfield County Fair is $10. Once you are inside, it costs x dollars to go on each ride. When BeckWhen Andrew makes chocolate chip cookies at home, he typically mixes x ounces of chocolate chips into the batter. In his last batch, he decided to make the cookies extra delicious and used 30% more chocolate chips.y went to the fair last weekend, she went on 4 rides.
Answers
The total cost for Beck to attend the fair and go on 4 rides can be calculated as follows:
Cost of admission: $10
Cost of 4 rides: 4x
Total cost: $10 + 4x
Since we are not given the value of x, we cannot calculate the total cost. However, we know that each ride costs x dollars, so we can use this information to find the cost of each ride if we are given the total cost. Alternatively, if we are given the cost of each ride, we can find the total cost by substituting the value of x into the equation.
As the question does not provide any information about the value of x or the total cost, we cannot provide a specific answer to this question.
Anna has a loyalty card good for a 7% discount at her local grocery store. What number should she multiply the prices on the tags by to find the price she would have to pay, before tax, in one step?
Answers
Anna should multiply the prices on the tags by 0.93 to find the price she would have to pay before tax in one step.
Given that Anna has a loyalty card good for a 7% discount at her local grocery store.
We have to find the number should she multiply the prices on the tags by to find the price she would have to pay, before tax
Anna should multiply the prices on the tags by 0.93 (which is 1 minus the 7% discount) to find the price she would have to pay before tax in one step.
For example, if an item costs $10 before the discount, Anna would pay $10 x 0.93 = $9.30 after the discount.
Hence, Anna should multiply the prices on the tags by 0.93 to find the price she would have to pay before tax in one step.
To learn more on Percentage click:
https://brainly.com/question/24159063
#SPJ1
There are 365 days in a year and 24 hours in a day. How Many hours are in 4 years?
Answers
Answer: 8,760 Hours
Step-by-step explanation:
Write the equation of the line graphed below.

Answers
Williamsburg 3 1/2 hours playing his video game on Monday he spent another 2 1/2 hours playing on Wednesday how many hours did he play all together
Answers
Answer:
6 hours
Step-by-step explanation:
3 plus 2 equals 5 and 1/2+1/2=6
The parabola in the image has its focus at (4,3). Its directrix is the line y=1. The point (8,6) is on the parabola.
4
3
2
ol
Answers
Answer
:
Step-by-step explanation:
Which of the following two sets are equal? \( A=\{1,2,3\} \) and \( B=\{2,1,3\} \) \( A=\{1,2\} \) and \( B=\{1\} \) \( A=\{1,2,4\} \) and \( B=\{1,2,3\} \) \( A=\{1,2\} \) and \( B=\{1,2,3\} \)
Answers
The sets that are equal are A = {1, 2, 3} and B = {2, 1, 3}
The order of elements does not matter when determining the equality of sets. Both sets A and B contain the same elements, namely 1, 2, and 3, even though their order is different. Therefore, we can say that A and B are equal sets.
The other sets mentioned, A = {1, 2} and B = {1}, A = {1, 2, 4} and B = {1, 2, 3}, and A = {1, 2} and B = {1, 2, 3}, are not equal because they have different elements. In the first case, set A has two elements, while set B has only one element.
In the second case, set A contains the element 4, which is not present in set B.
In the third case, set A has two elements, while set B has three elements, including the element 3, which is not present in set A.
for such more question on sets
https://brainly.com/question/29870206
#SPJ8

Is direct variation the same as slope?
Answers
Answer:
Step-by-step explanation:
A direct variation is a linear relationship between variables so they have a constant ratio. It is a special case of the slope-intercept form y =mx +b, where b = 0.
Lol, it seems like nobody helps anyone here anymore. It’s just full of bots
Answers
Answer:
Nah i gotcha, I'm always helping around people, as long as i understand the question myself Imfao
A scientist mixes water (containing no salt) with a solution that contains 40% salt. she wants to obtain 120 ounces of a mixture that is 35% salt. how many ounces of water and how many ounces of the 40% salt solution should she use?
Answers
She must use 187.5 ounces of water and 62.5 ounces of salt solution for her experiment.
What is an equation?
The definition of an equation in algebra is a mathematical statement that proves two mathematical expressions are equal. Consider the equation 3x + 5 = 14, where 3x + 5 and 14 are two expressions that are separated by the symbol "equal."
The smallest equivalent fraction of the number is the form that is the simplest. How to find the most basic form: In the numerator and denominator, look for shared factors. Examine the fraction to see if one of the numbers is a prime number.
Say w= the amount of water in oz, then the 60% of the solution is 250 - w
Set up the equation:
Use distributive property first
0.60(250-w) = 0.15 x 250
Isolate to solve for w
150- 0.60w= 37.5
-0.60w= 37.5-150
0.60w= -112.5
w= 187.5 ounces
250-187.5= 62.5 ounces salt solution
Therefore, she must use 187.5 ounces of water and 62.5 ounces of salt solution for her experiment.
To learn more about distributive property refer to:
https://brainly.com/question/2807928
#SPJ1
A meter is to be bolted to a switchboard. The meter studs that will fit into the holes on the switchboard are 0.4365 -inch in diameter. What are the hole sizes, expressed in decimal form, if they are to be 1.32-inch larger in diameter than the studs
Answers
The hole size required for the meter to be bolted to the switchboard is 1.7565 inches in diameter, expressed in decimal form.
To find the hole size for the meter to be bolted to the switchboard, you need to add the given diameter difference of 1.32 inches to the diameter of the meter studs. The meter studs are 0.4365 inches in diameter. So, the calculation is as follows:
Hole size = Meter stud diameter + Diameter difference
Hole size = 0.4365 inches + 1.32 inches
Hole size = 1.7565 inches
Know more about diameter here:
https://brainly.com/question/5501950
#SPJ11
a committee will be formed with 4 managers and 4 engineers selected randomly without replacement from 11 managers and 16 engineers. what is the probab
Answers
The probability that engineer Jane or manager Mary is on the committee will be 1/11 formed with 4 managers and 4 engineers selected randomly without replacement from 11 managers and 16 engineers.
The probability of an event is a number that indicates how likely the event is to occur. It is expressed as a number in the range from 0 and 1, or, using percentage notation, in the range from 0% to 100%.
Probability = Expected/Total outcome
If 4 managers were randomly selected from 11 managers, the probability will be 4/11.
If 4 engineers were randomly selected from 16 engineers, the probability will be 4/16.
The probability that engineer Jane or manager Mary is on the committee will be -
= 4/11 * 4/16
= 1/11
Therefore, the probability is 1/11.
The given question is incomplete, the given question is given below :
A committee will be formed with 4 managers and 4 engineers selected randomly without replacement from 11 managers and 16 engineers. What is the probability that engineer Jane or manager Mary is on the committee?
To know more about probability
https://brainly.com/question/30034780
#SPJ4
Action video rents dvds and video games to its customers. The cost to rent d, DVD movies, is $3.50 each and the cost to rent r, video games, is $2.50 each. Which of these represents the possible number of DVDs that could be rented for no more that $20?
Answers
Answer:
d = 5.71
Step-by-step explanation:
Let
Quantity of DVD movies = d
Quantity of Video games = r
Price of DVD movies = $3.50
Price of video games = $2.50
Total budget plan for DVD movies= $20
Which of these represents the possible number of DVDs that could be rented for no more that $20
Price of DVD movies × Quantity of DVD movies = $20
$3.50 × d = $20
3.50d = 20
Divide both sides by 3.50
d = 20/3.50
= 5.71
Approximately to the nearest whole number = 6
hello please help thanks

Answers
Answer:
oceans and the Sun
Step-by-step explanation:
The Sun heats ocean water causing some to evaporate. Tides move the ocean water. Waves move ocean water onto the shore.
assume that the diameter d of a circle is a differentiable function of t, and let c be the circumference of the circle. find an equation that relates d times c divided by d times t and times d divided by d times t. c = πd d times c divided by d times t is equal to pi times d d times c divided by d times t is equal to pi times the quantity d times d divided by d times t end quantity d times c divided by d times t is equal to pi times d times the quantity d times d divided by d times t end quantity
Answers
The relationship between the diameter (d) and circumference (c) of a circle can be expressed by the equation d * c / (d * t) = π * (d * d) / (d * t), where t represents a variable related to time.
The equation d * c / (d * t) = π * (d * d) / (d * t) relates the diameter (d), circumference (c), and a variable (t) that is likely associated with time or another independent parameter. This equation demonstrates a relationship between these variables in terms of their derivatives.
To understand the equation, let's break it down. The left side of the equation, d * c / (d * t), represents the rate of change of the circumference with respect to the variable t. Similarly, the right side of the equation, π * (d * d) / (d * t), represents the rate of change of π * (d * d) with respect to t.
By setting these two rates of change equal to each other, the equation establishes a relationship between the derivative of the circumference and the derivative of π * (d * d) with respect to t. This equation can be useful in studying the dynamics or properties of circles where the diameter varies over time or another parameter.
Overall, the equation relates the derivatives of the diameter, circumference, and another variable, providing a mathematical expression to describe their relationship.
Learn more about circumference here:
https://brainly.com/question/28757341
#SPJ11
Krystal wanted to buy her favorite jeans while they were on sale. The original price of the jeans was $50 and was reduced to $25 dollars after the sale. What percentage was the price of the jeans reduced?
Answers
7x-4y=3y-14 What is the literal equation for y.
Answers
Answer:
Step-by-step explanation:
7x - 4y = 3y - 14
7x - 7y = -14
-7y = -7x - 14
y = x + 2
Answer:
7x-4y-3y = -14 (bring the positive 3 towards the other side)
7x-7y = -14
-7y = -14-7x (since the question asks for y, bring the x to the other side to leave y with its coefficient)
y = (-14-7x) ÷ -7 (divide the whole equation by -7 to leave the y by itself)
y = 2+x
professor salton's research is about the relationship between work and study among college students. in his survey, he asked respondents to report how many hours they work for a non-academic job. professor salton's measure for work is:
Answers
Professor Salton's measure for work is the number of hours worked for a non-academic job, as reported by respondents in his survey.
This measure is a simple but effective way to gain an understanding of how work can impact a student's academic studies. It provides a direct measure of the amount of time that students spend working outside their academic pursuits, and can be used to quantify the potential effects of working on their educational success.
By taking this measure, Professor Salton has provided an effective way of analyzing the relationship between work and study. It allows researchers to determine whether working has an impact on student performance and academic outcomes. It also allows researchers to investigate whether certain types of work, such as part-time or full-time employment, have more of an impact than others.
Ultimately, this measure is an invaluable tool for researchers to gain a better understanding of the effects of work on student success.
See more about measure at: https://brainly.com/question/30925181
#SPJ11
Find the value of x.

Answers
Answer:
x=67.5
Step-by-step explanation:
The interior angles of a triangle add up to 180. therefore
45+x+x=180
2x=135
x=67.5
Answer:
x=67.5
Step-by-step explanation:
180-45=135
135/2
67.5
What's the answer for?
One and one third + one and one three fourth
Answers
one and one third + one and three fourths equals three and one twelfth (3 1/12).
To add these two mixed numbers, we need to convert them to improper fractions:
1 and 1/3 = 4/3
1 and 3/4 = 7/4
Now we can add the two fractions:
4/3 + 7/4
To add fractions with different denominators, we need to find a common denominator. In this case, the least common multiple of 3 and 4 is 12:
4/3 + 7/4 = (16/12) + (21/12)
= 37/12
Now we can convert the improper fraction back to a mixed number:
37/12 = 3 and 1/12
what is number?
In mathematics, a number is a quantity that represents a magnitude or size of a particular quantity or measurement. Numbers can be classified into different categories such as whole numbers, integers, rational numbers, irrational numbers, real numbers, and complex numbers.
To learn more about numbers visit:
brainly.com/question/17429689
#SPJ11