Subtract.
78.9−5.64 Pls help
Answers
Answer:
73.26
Step-by-step explanation:
I hope this helps :)
Answer:
73.26 is your answer.
Step-by-step explanation:
Related Questions
what two ratios equivalent to the ratio of 9/4?
Answers
Answer: Ratio 4:9 is also 49 . This ratio is in reduced form (no whole can be divided into both evenly).
Step-by-step explanation:
Answer:
Step-by-step explanation:
1. 9/4= 9/4 ÷ 2=?
2. 9/4 ÷2= 1.125
3. 1.125= 9/8 = 9:8
Solve the system of equations.
\begin{aligned} & -4x+3y = -2 \\\\ & y=x-1 \end{aligned}
−4x+3y=−2
y=x−1
Answers
Answer:
x = -1 ; y=0
Step-by-step explanation:
We plug in the y, from the second equation, in the first one. By doing so we obtain:
-4x +3(x-1) = -2
-4x + 3x - 3 =-2
-x = 1
x= -1
Now we take this value and plug it in the second equation:
y = 1-1 = 0
Solution:
(-1,0)
-4x+3x-3=-2
-4x+3x=-2+3
-x=1
x=-1
y=-1-1
y=-2
(x,y)
(-1, -2)
Find the slope of the tangent line to the curve defined by 4x2+5xy+y4=370
at the point (−9,−1)
Answers
Answer:
The slope of the tangent line to the curve at the given point is -11/7.
Step-by-step explanation:
Differentiation is an algebraic process that finds the gradient (slope) of a curve. At a point, the gradient of a curve is the same as the gradient of the tangent line to the curve at that point.
Given function:
\(4x^2+5xy+y^4=370\)
To differentiate an equation that contains a mixture of x and y terms, use implicit differentiation.
Begin by placing d/dx in front of each term of the equation:
\(\dfrac{\text{d}}{\text{d}x}4x^2+\dfrac{\text{d}}{\text{d}x}5xy+\dfrac{\text{d}}{\text{d}x}y^4=\dfrac{\text{d}}{\text{d}x}370\)
Differentiate the terms in x only (and constant terms):
\(\implies 8x+\dfrac{\text{d}}{\text{d}x}5xy+\dfrac{\text{d}}{\text{d}x}y^4=0\)
Use the chain rule to differentiate terms in y only. In practice, this means differentiate with respect to y, and place dy/dx at the end:
\(\implies 8x+\dfrac{\text{d}}{\text{d}x}5xy+4y^3\dfrac{\text{d}y}{\text{d}x}=0\)
Use the product rule to differentiate terms in both x and y.
\(\boxed{\dfrac{\text{d}}{\text{d}x}u(x)v(y)=u(x)\dfrac{\text{d}}{\text{d}x}v(y)+v(y)\dfrac{\text{d}}{\text{d}x}u(x)}\)
\(\implies 8x+\left(5x\dfrac{\text{d}}{\text{d}x}y+y\dfrac{\text{d}}{\text{d}x}5x\right)+4y^3\dfrac{\text{d}y}{\text{d}x}=0\)
\(\implies 8x+5x\dfrac{\text{d}y}{\text{d}x}+5y+4y^3\dfrac{\text{d}y}{\text{d}x}=0\)
Rearrange the resulting equation in x, y and dy/dx to make dy/dx the subject:
\(\implies 5x\dfrac{\text{d}y}{\text{d}x}+4y^3\dfrac{\text{d}y}{\text{d}x}=-8x-5y\)
\(\implies \dfrac{\text{d}y}{\text{d}x}(5x+4y^3)=-8x-5y\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=\dfrac{-8x-5y}{5x+4y^3}\)
To find the slope of the tangent line at the point (-9, -1), substitute x = -9 and y = -1 into the differentiated equation:
\(\implies \dfrac{\text{d}y}{\text{d}x}=\dfrac{-8(-9)-5(-1)}{5(-9)+4(-1)^3}\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=\dfrac{72+5}{-45-4}\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=-\dfrac{77}{49}\)
\(\implies \dfrac{\text{d}y}{\text{d}x}=-\dfrac{11}{7}\)
Therefore, slope of the tangent line to the curve at the given point is -11/7.
I don’t have a question this is just the answer:))

Answers
Factor the expression -8x 2+ 22x - 15
Answers
From 1985 to 2007, the number B B of federally insured banks could be approximated by B ( t ) = − 329.4 t + 13747 B(t)=-329.4t+13747 where t is the year and t=0 corresponds to 1985. How many federally insured banks were there in 1990?
Answers
Answer:
12100
Step-by-step explanation:
If the number B of federally insured banks could be approximated by B ( t ) = − 329.4 t + 13747 from 1985 to 2007 where t = 0 correspond to year 1985
In order to determine the amount of federally insured banks that were there in 1990, we will first calculate the year range from initial time 1985 till 1990
The amount of time during this period is 5years. Substituting t = 5 into the modeled equation will give;
B ( t ) = − 329.4 t + 13747
B(5) = -329.4(5) + 13747
B(5) = -1647+13747
B(5) = 12100
This shows that there will be 12100 federally insured banks are there in the year 1990.
Part A: Choose one value for a and one value for b that would make both of the following inequalities true:
a < b and |b| < |a|
Answers
The correct answer is, by choosing a = -2 and b = 1, we satisfy both inequalities .a < b:
To make both inequalities true, we need to select values for a and b that satisfy the given conditions:
a < b: This inequality means that the value of a should be less than the value of b.
|b| < |a|: This inequality means that the absolute value of b should be less than the absolute value of a.
One possible solution that satisfies both conditions is:
a = -2
b = 1
With these values, we have:
-2 < 1 (a < b)
|-1| < |2| (|b| < |a|)
Therefore, by choosing a = -2 and b = 1, we satisfy both inequalities.a < b:
This inequality states that the value of a should be less than the value of b. In other words, a needs to be positioned to the left of b on the number line. To satisfy this condition, we can choose a to be any number that is less than b. In the example I provided, a = -2 and b = 1, we can see that -2 is indeed less than 1, fulfilling the requirement.
|b| < |a|:
This inequality involves the absolute values of a and b. The absolute value of a number is its distance from zero on the number line, always resulting in a non-negative value. The inequality states that the absolute value of b should be less than the absolute value of a. To satisfy this condition, we can choose b to be any number with a smaller absolute value than a. In the example I provided, |1| is less than |(-2)|, as 1 is closer to zero than -2, fulfilling the requirement.
By selecting a = -2 and b = 1, we satisfy both inequalities: a < b and |b| < |a|. The specific values of -2 and 1 were chosen as an example, but there are multiple other values that would also satisfy the given conditions. The important aspect is that a is indeed less than b, and the absolute value of b is smaller than the absolute value of a.
Learn more about inequality here:
https://brainly.com/question/30238989
#SPJ8
has 600 feet of fencing to use in making a yard for her new puppyThe yard she has planned has a length that is 75 feet less than twice the widthWhat are the dimensions of the yard
Answers
The dimension of the yard is 175ft x 125 ft.
Given that,
L = length = 2W-75 feet
P = perimeter = 600 feet
Since yard is have a rectangular size,
And rectangles are four-sided polygons with all internal angles equal to 90 degrees. At each corner or vertex, two sides meet at right angles. The rectangle differs from a square in that its opposite sides are equal in length.
W = width;
Since, perimeter is 2 times of sum of length and width of rectangle.
P=2(L+W)
⇒600ft=2(L+W)
Divide each side by 2.
300 feet = L+W
L can be substituted.
300ft = 2W-75ft + W Take 75 feet off each side.
375 ft = 3W
Divide each side by three to get
W = 125 ft
It is 125 feet wide.
L=2W-75ft
L=2(125ft)-75ft
L=250ft-75ft
L=175ft
Thus dimension is 175ft x 125 ft.
Learn more about the rectangle visit:
https://brainly.com/question/2607596
#SPJ1
DAC = 2x+4 and BAC= 3x +1

Answers
Answer:
x=17
Step-by-step explanation:
Since ABCD is a rectangle, ∠DAB=90.
∠DAB=∠DAC+∠BAC
90=(2x+4)+(3x+1)
90=5x+5
5x=85
x=17
1.2.2 Determine the total cost of the HP'LASER JET'?
Answers
Answer:
£139.98
Step-by-step explanation:
£139.99
SAVE
£0.01
£139.98
VAT incl.
A candle is burning. It starts out 12 inches long. After 1 hour, it is 10 inches long. After 3 hours, it is 5.5 inches
1. Explain one reason why it might be reasonable to model the relationship between time and height of the candle with a linear function.
2. Explain one reason it might NOT be reasonable to model this relationship with a linear relationship
Answers
The reasons for (1) and (2) are added below
Why it is reasonable to use a linear functionOne reason why it might be reasonable to model the relationship between time and height of the candle with a linear function is that the rate of change of the candle's height appears to be constant over time.
Why it is unreasonableOne reason why it might NOT be reasonable to model this relationship with a linear function is that the candle's height cannot continue to decrease indefinitely.
This means that the candle's height is bounded and cannot continue to decrease linearly forever.
Read more about functions at
https://brainly.com/question/2030026
#SPJ1
Find the equation of the line that passes through (-4, 2) and is perpendicular to the line that goes through (-4, 6) and (5, 2).
Answers
Answer:
9x -4y = -44
Step-by-step explanation:
You want the equation of the line through (-4, 2) and perpendicular to the line through (-4, 6) and (5, 2).
Equation of a LineThe equation of a line through (h, k) and perpendicular to the line through (x1, y1) and (x2, y2) can be written as ...
(x2 -x1)(x -h) +(y2 -y1)(y -k) = 0
Using the given points, this becomes ...
(5 -(-4))(x -(-4)) +(2 -6)(y -2) = 0
9(x +4) -4(y -2) = 0
Expanding this gives the general form equation:
9x -4y +44 = 0
Subtracting the constant gives the standard form equation:
9x -4y = -44

Question 2. Determine the height of the tower.

Answers
The height of the tower is h = 0. 079 km
How to determine the heightFrom the information given, we have that;
AB = 1.1 km
h = unknown
h = a tan 6
h = b tan 13
Equate the expression for height, we have;
a tan 6= b tan 13
But we have that;
a + b = AB = 1.1
Then, we get;
a tan 6 = (1.1 - a) tan 13
a tan 6 = 1.1 tan 13 - a tan 13
a( tan 6 + tan 13) = 1.1 tan 13
Divide by the coefficient, we get;
a = 0.756km
But we have that;
h = a tan 6
h = 0.756 tan 6
h = 0. 079 km
Learn more about trigonometric identities at: https://brainly.com/question/7331447
#SPJ1
what are the features of the function g if g(x)= f(x+4) +8
Answers
The domain, range, x-intercept, or y-intercept of g(x) = f(x + 4) + 8. The features of g depend on the corresponding features of f.
Given the function g(x) = f(x + 4) + 8, let's examine its features:
Domain:
The domain of the function g will be the same as the domain of the function f, which depends on the restrictions or constraints of f. However, it is important to note that shifting the input by 4 units (x + 4) does not inherently change the domain unless there are specific restrictions imposed by f.
Range:
Similar to the domain, the range of the function g will depend on the range of the function f.
x-intercept:
The x-intercept of a function is the point where the graph intersects the x-axis, meaning the y-coordinate is zero (y = 0). To find the x-intercept of g(x), we set g(x) = 0 and solve for x.
0 = f(x + 4) + 8
By subtracting 8 from both sides:
-8 = f(x + 4)
Since the exact value of x that makes f(x + 4) equal to -8. The x-intercept will depend on the behavior of f.
y-intercept:
The y-intercept of a function is the point where the graph intersects the y-axis, meaning the x-coordinate is zero (x = 0). To find the y-intercept of g(x), we substitute x = 0 into the function:
g(0) = f(0 + 4) + 8
g(0) = f(4) + 8
Again, the specific value of f(4) will depend on the behavior of the function f.
for such more question on function
https://brainly.com/question/14723549
#SPJ8
Let's roll two dice and find the probability of rolling a certain sum. Is this a simple or compound event?
Two dice - Red and Blue
Recall that a simple event has one and only one outcome of interest. In this example, we are rolling two dice, but we are only interested in one outcome, the sum of the two dice. This is a simple event.
What is the probability of:
Rolling a sum of 1?
Rolling a sum of 3?
Rolling a sum of 12?
Rolling a sum of 7?
Since we are rolling a pair of dice and looking for the sum, the sample space is a little more complicated than rolling one die. The chart below will help us determine the possible outcomes. The top row indicates the numbers on the sides of the blue die and the first column represents the number on the sides of the red die. The white area indicates the sum of the numbers in the row and column.
# Rolled 1 2 3 4 5 6
1 1+1=2
1
+
1
=
2
1+2=3
1
+
2
=
3
1+3=4
1
+
3
=
4
1+4=5
1
+
4
=
5
1+5=6
1
+
5
=
6
1+6=7
1
+
6
=
7
2 2+1=3
2
+
1
=
3
2+2=4
2
+
2
=
4
2+3=5
2
+
3
=
5
2+4=6
2
+
4
=
6
2+5=7
2
+
5
=
7
2+6=8
2
+
6
=
8
3 3+1=4
3
+
1
=
4
3+2=5
3
+
2
=
5
3+3=6
3
+
3
=
6
3+4=7
3
+
4
=
7
3+5=8
3
+
5
=
8
3+6=9
3
+
6
=
9
4 4+1=5
4
+
1
=
5
4+2=6
4
+
2
=
6
4+3=7
4
+
3
=
7
4+4=8
4
+
4
=
8
4+5=9
4
+
5
=
9
4+6=10
4
+
6
=
10
5 5+1=6
5
+
1
=
6
5+2=7
5
+
2
=
7
5+3=8
5
+
3
=
8
5+4=9
5
+
4
=
9
5+5=10
5
+
5
=
10
5+6=11
5
+
6
=
11
6 6+1=7
6
+
1
=
7
6+2=8
6
+
2
=
8
6+3=9
6
+
3
=
9
6+4=10
6
+
4
=
10
6+5=11
6
+
5
=
11
6+6=12
6
+
6
=
12
How many outcomes are in the sample space? Answer
Answers
Answer:
the answer to your question how many outcomes is really gonn adepend on you you slove you problem but my amswer is gonna be 7.
The following are the ages (years) of 5 people in a room:
18, 25, 18, 21, 16
A person enters the room.
The mean age of the 6 people is now 25.
What is the age of the person who entered the room?
Answers
Explanation:
Let x be the age of the person who enter the room
(18 + 25 + 18 + 21 + 16 + x)/6 = 25
(77 + x)/6 = 25
77 + x = 25(6)
77 + x = 150
x = 150 - 77
x = 73
Solve for x in 2•8 X 867•5x
Answers
Step-by-step explanation:
867.5x ×2.8
is is equal to 2429x
Write the coordinates of the vertices after a reflection over the x-axis. 1072
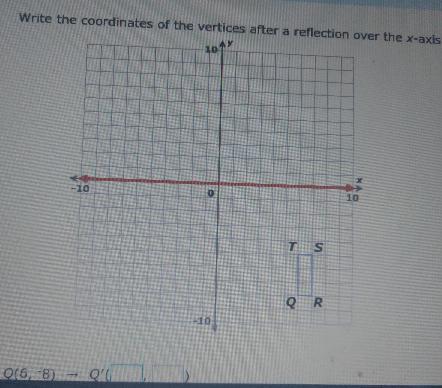
Answers
The reflection about x-axis results in same x coodinate with oppositive of y coordinate. It can be expressed as,
\((x,y)\rightarrow(x,-y)\)Determine the coordinates of the vertices after reflection over the x-axis.
\(Q(6,-8)\rightarrow Q^{\prime}(6,8)\)\(R(7,-8)\rightarrow R^{\prime}(7,8)\)\(S(7,-5)\rightarrow Q^{\prime}(7,5)\)\(T(6,-5)\rightarrow T^{\prime}(6,5)\)(40 POINTS!!) WRITE AN EQUATION FOR EACH SITUATION !
(Each package weighs 64 pounds)
a. each package contains 4 boxes. Each box contains a 7 pound bag of beans and a bag of rice. The rice bags are identical.
b. Each package contains 4 identical bags of rice and a 7 pound bag of beans
Answers
Answer:
Answer is below
Step-by-step explanation:
A. 64 / 4 - 7
B. 9 / 4 = 2.25
A. (Each box is 16 pounds) (Rice weighs 9 pounds)
Based on the information in the table, what
was the approximate value of this item in
1980?

Answers
Answer:
B) 4,700
Step-by-step explanation:
6000 - 4000 = 2000
2000 in 15 year, find how much for each year
2000/ 15 = 133.3333333
133.3333333 estimated = 133
133 approximately for each year
1975 to 1980 is five years
133 x 5 = 665
4000 + 665 = 4665
4665 rounded the the nearest hundred
4700
The area of a rectangle is 2 square feet. The perimeter of the rectangle
is 9 ft. Find the length, 1, and width, w, of the rectangle. What is 12 + W2?
Answers
Answer:
The area of the rectangle is 72 square feet
Step-by-step explanation:
what is the absolute value of -0.575
Answers
Answer:
hQIwgqhioiojhwvjia I VJILAija IOJA iojiao JIOA JIOJIA JIoj ijioJ Jjio ji jijioJI JIioj jio
Step-by-step explanation:
ADD 34
Point: (2,7)
Reflected across y-axis: (-2,7)
Reflected across x-axis: ????
My options for the answer is
(-7,-2)
(-2,7)
(2,-7) which answer is it I have already tried the first one and it said it was wrong.
Answers
Answer:
(2,-7)
Step-by-step explanation:
Reflection rule for across the x-axis: \((x,y)\rightarrow (x,-y)\)
Using the rule and point (2,7):
\((2,7)\rightarrow(2,-7)\)
(2,-7) should be the correct answer.
Brainilest Appreciated.
Indicate which formula you would use to solve for the missing side B and then write your answer correct to two decimal places.Write only the formula down.. Single line text.
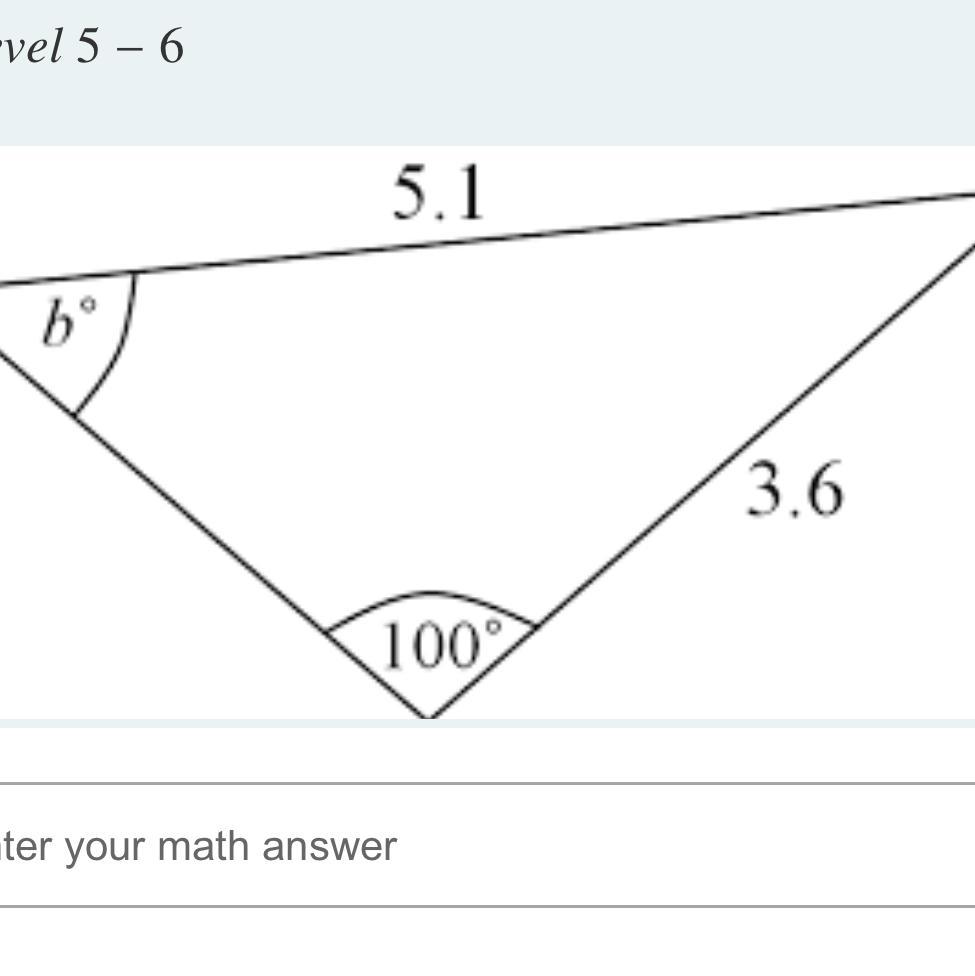
Answers
Answer:
The measure of the angle \(b\) is approximately 44.040°.
Step-by-step explanation:
We need to apply Law of the Sine to determine the value of angle \(b\), since the length of the side opposite to this side and another side length and its opposite angle are known. That is:
\(\frac{3.6}{\sin b} = \frac{5.1}{\sin 100^{\circ}}\)
\(\sin b = \frac{3.6}{5.1}\times \sin 100^{\circ}\)
\(b = \sin^{-1}\left(\frac{3.6}{5.1}\times \sin 100^{\circ} \right)\)
\(b \approx 44.040^{\circ}\)
The measure of the angle \(b\) is approximately 44.040°.
There were 5 babies born at a hospital in one day. One baby was male and four were female. If a baby is as likely to be a male as a female, find the probability of this outcome by expanding (m +f)5. Round to the nearest percent if necessary.
Answers
Answer:
If four babies are born in a given hospital on the same day, the outcome that all four will be boys is
1/2^4=1/16
The outcome that three will be boys and one a girl would be 4x1/2^3x1/2=1/4
the outcome that two will be boys and 2 will be girls is
6x1/2^2x1/2^2=3/8
Step-by-step explanation:
I am struggling to find domain and range please help thank you

Answers
Answer:
Domain: 0, 1, 2, 3, 4,
Range: 1, 2, 3, 4, 5,
Step-by-step explanation:
Based on the graph the domain of the function is 0, 1, 2, 3, 4, and the range is 1, 2, 3, 4, 5, therefore, the answer is:
hey can i get help here? im just a middle schooler and my school just jumped into this with no explanation. so far highschoolers helped me understand it more than any teacher could. so in those terms, thank you so much!

Answers
Answer:
the closest answer is the last option, so I would say that is the correct one.
Step-by-step explanation:
4.5 x 4.5 x π =
20.25 x π =
63.6172....
Past insurance company audits have found that 2 percent of dependents claimed on an employee’s health insurance actually are ineligible for health benefits. An auditor examines a random sample of 7 claimed dependents. (a) What is the probability that all are eligible? (b) That at least one is ineligible?
Answers
Using the binomial distribution, it is found that the probabilities are given by:
a) 0.8681 = 86.81%.
b) 0.1319 = 13.19%.
What is the binomial distribution formula?The formula is:
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
The parameters are:
x is the number of successes.n is the number of trials.p is the probability of a success on a single trial.In this problem, we have that:
98% of the employees are eligible, hence p = 0.98.A sample of 7 was taken, hence n = 7.Item a:
The probability is P(X = 7), hence:
P(X = 7) = 0.98^7 = 0.8681 = 86.81%.
Item b:
The probability is:
P(X < 7) = 1 - P(X = 7) = 1 - 0.8681 = 0.1319 = 13.19%.
More can be learned about the binomial distribution at https://brainly.com/question/24863377
The diameter of a standard dart board is 18”. What is the area of the dart board?
Answers
Find the gcf of the following numbers using continuous division. Write ur answer
1.) 24 and 72
3.) 24,32 and 48
2.) 18,27 and 45
4.) 24 and 36
Pls answer I need it thank you!
Answers
Answer:
Step-by-step explanation:
The continuous division method is an effective method to determine the GCF of two or more numbers, aside from the listing method where we are listing down the common factors before determining the greatest among them.
In continuous division, we are just simply dividing the numbers by their common factors until such time that we find no more common factors except for 1 to them to be divided. After which, we will just multiply the common factors that we used to divide them. The result will be our GCF. Let us try the exercise given above:
1. Find the GCF of 24 and 72
2 / 24 72
2 / 12 36
2 / 6 18
3 / 3 9
/ 1 3
Since we keep on dividing the numbers by 2 for 3 repetitions, we arrived at 3 and 9 by which we divide by 3 and we get 1 and 3 which we can no longer divide. So the GCF is: 2x2x2x3 = 24
Therefore, the GCF of 24 and 72 is 24.
2. Find the GCF of 24, 32 and 48
2 / 24 32 48
2 / 12 16 24
2 / 6 8 12
/ 3 4 6
So the GCF is: 2x2x2 = 8
Therefore, the GCF of 24, 32 and 48 is 8.
3. Find the GCF of 18, 27 and 45.
3 / 18 27 45
3 / 6 9 15
/ 2 3 5
So the GCF is: 3x3 = 9
Therefore, the GCF of 18, 27 and 45 is 9.
4. Find the GCF of 24 and 36.
2 / 24 36
2 / 12 18
3 / 6 9
/ 2 3
So the GCF is 2x2x3 = 12
Therefore, the GCF of 24 and 36 is 12.