State the domain of the function y = 3x+1.
Answers
The domain of the function y = 3x+1 is the set of all real values
How to determine the domain?From the question, we have the following parameters that can be used in our computation:
Function: y = 3x + 1
The above function is a linear function
A linear function can take any real number as its input
This means that the domain of the function contains all real values
Read more about domain at
https://brainly.com/question/13146216
#SPJ1
Related Questions
Triangle ABC is shown in the xy-coordinate plane. It will be rotates 90 degrees clockwise about the origin to form triangle A'B'C'. Graph the correct orientation of A'B'C' in the coordinate plane
Answers
For a 90 degrees clockwise rotation,
A' = (y, -x) = (1, -2)
B' = (y, -x) = (3, -3)
C' = (y, -x) = (2, -5)
How to graph a triangleTo plot a triangle onto a coordinate plane, these instructions must be followed:
Begin by drawing x and y axes to establish the necessary framework.
Choose three points upon which to place the vertices of the triangle on the graph.
Then connect the selected points through straight lines, thus resulting in the appearance of three sides; representing each point's distance from one another respectively.
Subsequently attach letter designations such as A, B, and C to each vertex.
Lastly, inspect the measurements of the sides and angles between them to confirm that they correspond with requisites specific to your chosen triangle type (such as an equilateral or Isosceles shape).
Read more about triangles here:
https://brainly.com/question/1058720
#SPJ1


what are the zeros of the function represented by the quadratic expression 2x^2 + x - 3?
A: x= -3/2 and x= 1
B: x= -2/3 and x= 1
C: x= -1 and x= 2/3
D: -1 and x= -3/2
Answers
T is the midpoint of PQ. PT=3x+8 and TQ = 5x-8. What is PT?
Answers
Answer:
PT = 32
Step-by-step explanation:
From the question, we are told that:
T is the midpoint of PQ
This means:
PT = TQ
PT=3x+8 and TQ = 5x-8
Step 1
We solve for x
3x + 8 = 5x - 8
Collect like terms
8 + 8 = 5x - 3x
16 = 2x
x = 16/2
x = 8
Step 2
We can solve for PT now
PT=3x+8
x = 8
PT = 3×8 + 8
PT = 24 + 8
PT = 32
Therefore, PT = 32
a rectangular poster has an area of 24 \large ft^2. the height of the poster is 6 feet less than three times its width. find the dimensions of the poster.
Answers
The dimensions of the rectangular poster are 4 feet in width and 6 feet in height.
To find the dimensions of the rectangular poster with an area of 24 ft^2 and height being 6 feet less than three times its width, we can follow these steps:
Let the width of the poster be represented by the variable w (in feet).
According to the given information, the height of the poster is 6 feet less than three times its width. We can express this as: height = 3w - 6.
The area of a rectangle is calculated by multiplying its width and height. So, we have the equation: area = width * height.
Substitute the given area and the expression for height into the equation: 24 = w * (3w - 6).
Solve the equation for w:
24 = w * (3w - 6)
24 = 3w^2 - 6w
0 = 3w^2 - 6w - 24
Factor the equation:
0 = 3(w^2 - 2w - 8)
0 = 3(w - 4)(w + 2)
Solve for w:
w - 4 = 0 => w = 4
w + 2 = 0 => w = -2 (discard this solution, as width cannot be negative)
Now that we've found the width (w = 4 feet), we can find the height by substituting w back into the height equation:
height = 3w - 6
height = 3(4) - 6
height = 12 - 6
height = 6 feet
So, the dimensions of the rectangular poster are 4 feet in width and 6 feet in height.
for more questions on rectangular
https://brainly.com/question/19819849
#SPJ11
Determine the length of the missing sides for each special right triangle. Leave answer in exact (reduced radical) form. Geometry!! pls help!!

Answers
Answer:
\(a = 18 \sqrt{3} \)
\(c = 36\)

4) Given f(x)=2x^5+5x^3−6x+2; find (a) f′ (1)= ? (b) f′′′ (2)= ?
Answers
f'(1) = 19. f'''(2) = 510.Given f(x)=2x^5+5x^3−6x+2: f'(1) = 19, f'''(2) = 510. To find the derivatives of the function f(x) = 2x^5 + 5x^3 - 6x + 2, we can use the power rule and the sum rule of differentiation.
(a) First, let's find f'(x), the first derivative of f(x): f'(x) = d/dx (2x^5) + d/dx (5x^3) - d/dx (6x) + d/dx (2) = 10x^4 + 15x^2 - 6. To find f'(1), we substitute x = 1 into the derivative: f'(1) = 10(1)^4 + 15(1)^2 - 6 = 10 + 15 - 6 = 19. Therefore, f'(1) = 19. (b) Now, let's find the third derivative f'''(x): f'''(x) = d^3/dx^3 (10x^4) + d^3/dx^3 (15x^2) - d^3/dx^3 (6). = 120x^2 + 30.
To find f'''(2), we substitute x = 2 into the third derivative: f'''(2) = 120(2)^2 + 30 = 120(4) + 30 = 480 + 30 = 510. Therefore, f'''(2) = 510.
To learn more about power rule click here: brainly.com/question/23418174
#SPJ11
What are the coordinates of the vertex of the function f(x) = x2 − 12x + 5?
(6, 31)
(−6, 31)
(6, −31)
(−6, −31)
Answers
Answer: (6, -31)
Explanation: See attachment

I need help please, I need this to be step by step word explained its solved already! THHANK YOU SO MUCH

Answers
Answer:
Step-by-step explanation:
Explanation in image

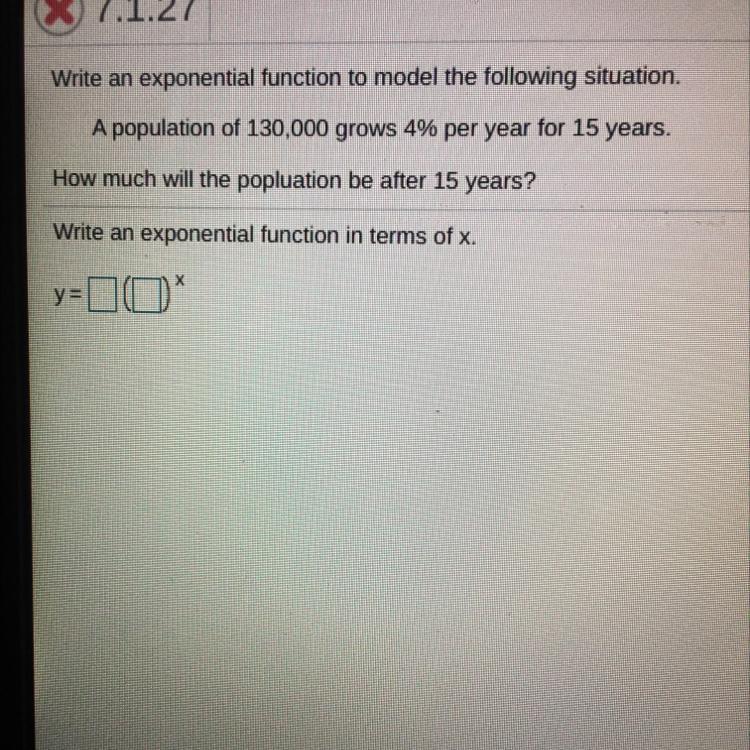
Write an exponential function to model the following situation.
A population of 130,000 grows 4% per year for 15 years.
How much will the popluation be after 15 years?
Write an exponential function in terms of x.
х
y=10
Answers
Answer:
234000
Step-by-step explanation:
Given data
population =130,000
Rate=4%
Time= 15 years
The expression for the growth is
y=P(1+r)^x
substitute
y=130000(1+0.04)^15
y=130000(1.04)^15
y=130000*1.800
y=234000
Hence the new population figure is 234000
COLOR THEME
Q ZOOM
1. Ace Cable TV offers two monthly plans. Plan A costs $55 a month plus $3 for each premium
channel the customer selects. Plan B costs $25 a month plus $8 for each premium channel
the customer selects. What number of channels will cause the cost of both plans to be the
same?
The anwsers
Answers
Selecting 6 premium channels will make the cost of both plans the same that will cause the cost of both plans to be the same, we need to set up an equation and solve for the unknown variable.
To find the number of channels that will cause the cost of both plans to be the same, we need to set up an equation and solve for the unknown variable. Let's assume the number of premium channels selected is represented by "x". For Plan A, the cost is $55 + $3x. For Plan B, the cost is $25 + $8x. To find the number of channels that will make the costs equal, we can set up the equation:
55 + 3x = 25 + 8x
Now, we can solve for "x". First, let's isolate the "x" term on one side of the equation by subtracting 3x from both sides:
55 - 25 = 8x - 3x
30 = 5x
Next, divide both sides by 5 to solve for "x":
x = 30 / 5
x = 6
To know more about cost,
https://brainly.com/question/28877940
#SPJ11
Use elementary row operations to transform the augmented coefficient matrix to echelon form. Then solve the system by back substitution. X₁-4x2 +5x3. = 23 2x₁ + x₂ + x3 = 10 -3x + 2x₂-3x3 = = -23 *** An echelon form for the augmented coefficient matrix is What is the solution to the linear system? Select the correct choice below and, if necessary, fill in the answer box(es) in your choice. OA. There is a unique solution, x₁ = x₂ = x3 - (Simplify your answers.) B. There are infinitely many solutions of the form x₁ = x2-x3-t where t is a real number. (Simplify your answers. Type expressions using t as the variable.) 21 OC. There are infinitely many solutions of the form x, .X₂S, X₁t where s and t are real numbers. (Simplify your answer. Type expression using s and t as the variables.) D. There is no solution.
Answers
The solution to the linear system is unique solution which is x₁ = 1/6, x₂ = 3/2, and x₃ = 17/6.
The correct answer is option A.
To solve the given system of linear equations using elementary row operations and back substitution, let's start by representing the augmented coefficient matrix:
[1 -4 5 | 23]
[2 1 1 | 10]
[-3 2 -3 | -23]
We'll apply row operations to transform this matrix into echelon form:
1. Multiply Row 2 by -2 and add it to Row 1:
[1 -4 5 | 23]
[0 9 -9 | -6]
[-3 2 -3 | -23]
2. Multiply Row 3 by 3 and add it to Row 1:
[1 -4 5 | 23]
[0 9 -9 | -6]
[0 -10 6 | -68]
3. Multiply Row 2 by 10/9:
[1 -4 5 | 23]
[0 1 -1 | -2/3]
[0 -10 6 | -68]
4. Multiply Row 2 by 4 and add it to Row 1:
[1 0 1 | 5/3]
[0 1 -1 | -2/3]
[0 -10 6 | -68]
5. Multiply Row 2 by 10 and add it to Row 3:
[1 0 1 | 5/3]
[0 1 -1 | -2/3]
[0 0 -4 | -34/3]
Now, we have the augmented coefficient matrix in echelon form. Let's solve the system using back substitution:
From Row 3, we can deduce that -4x₃ = -34/3, which simplifies to x₃ = 34/12 = 17/6.
From Row 2, we can substitute the value of x₃ and find that x₂ - x₃ = -2/3, which becomes x₂ - (17/6) = -2/3. Simplifying, we get x₂ = 17/6 - 2/3 = 9/6 = 3/2.
From Row 1, we can substitute the values of x₂ and x₃ and find that x₁ + x₂ = 5/3, which becomes x₁ + 3/2 = 5/3. Simplifying, we get x₁ = 5/3 - 3/2 = 10/6 - 9/6 = 1/6.
For more such information on: unique solution
https://brainly.com/question/31028007
#SPJ8
Honestly I don't know what to do at this point please help
Joe is working at the storage yard. It is 50 yards from the entrance (V) to the checkpoint (W). From there, it is 40 yards to the guard post (X). From his spot at the guard post, Joe notices a barrel tipped over 12 yards away (Z). The spill stretches to the fence (Y). If AXYZ is similar to AXVW, what is the distance d across the chemical spill? * zd Y 12 yd X 40 yd 50 yd W

Answers
Answer:
15 yds
Step-by-step explanation:
40 divided by 50 equals 4/5, so the lengths of the other triangle have to match that ratio. 3 fits into 12 four times and 15 five times, which makes it a four to five ratio.
find the sum or standard form of 10⁰+9⁰+7⁰+5⁰+3⁰+1¹⁰⁰
Answers
Answer:
6
Step-by-step explanation:
10⁰=1
9⁰=1
7⁰=1
5⁰=1
3⁰=1
1¹⁰⁰=1
so,
10⁰+9⁰+7⁰+5⁰+3⁰+1¹⁰⁰=1+1+1+1+1+1=6
Answer:
6
Step-by-step explanation:
We are working with exponents
Any number to the power of 0 is 1
a^0 = 1
1 to a power is 1
10⁰+9⁰+7⁰+5⁰+3⁰+1¹⁰⁰
1 + 1 + 1 + 1 + 1 + 1
6
49
11. What is the value of the expression m^3, when m=-8. (Hint: m to the the
third power)
Your answer
Answers
Hey there!
m^3
= -8^3
= -8 * -8 * -8
= 64 * -8
= -512
Therefore, your answer is: -512
Good luck on your assignment and enjoy your day!
~Amphitrite1040:)
The Fibonacci sequence 1, 1, 2, 3, 5, 8, 13, 21, … starts with two 1s, and each term afterward is the sum of its two predecessors. Which one of the ten digits is the last to appear in the ones position of a number in the Fibonacci sequence?
Answers
Answer:
6
Step-by-step explanation:
Note that any digits other than the units digit will not affect the answer. So to make computation quicker, we can just look at the Fibonacci sequence in $:
$1,1,2,3,5,8,3,1,4,5,9,4,3,7,0,7,7,4,1,5,6,....$
The last digit to appear in the units position of a number in the Fibonacci sequence is $6.
The last to appear in the ones position of a number in the Fibonacci sequence is \(6\).
The Fibonacci sequence \(1, 1, 2, 3, 5, 8, 13, 21\), … starts with two 1s, and each term afterward is the sum of its two predecessors.
The next terms are:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946.
Here, it can be seen that \(6\) is the last to appear in the ones position of a number in the Fibonacci sequence.
Learn more here:
https://brainly.com/question/13247630?referrer=searchResults
A marching band director needs to divide 44 members into two groups. He wants the ratio of band members in group 1 to band members in group 2 to be 1 to 3. How many band members will be in group 2?.
Answers
If the ratio of band members in group 1 to band members in group 2 is 1 to 3, then for every 3 band members in group 2, there will be 1 band member in group 1.Therefore, group 2 will have 11 band members.
What is ratio and proportion?Comparing two numbers or quantities results in a ratio. Usually, it is expressed in the form "a:b" or "a/b," with a and b standing for the two quantities under comparison. Contrarily, a percentage is an equation that states that two ratios are equal. Alternatively said, a proportion is a claim that one ratio is equal to another.
For example, if the ratio of apples to oranges in a basket is 2:3, this implies that there are three oranges per each two apples. We may alternatively state that the ratio of apples to total number of fruits in the basket is 2:5, because 2 + 3 = 5. The two ratios (2:3 and 2:5) are proportionate in this instance. Also, ratio of band members in group 1 to band members in group 2 to be 1 to 3
How to solve?
If the director wants to divide 44 band members into two groups, with this ratio, then the number of band members in group 2 will be 44 / (1 + 3) = 44 / 4 = 11 band members.
To learn more about ratio and proportion, visit:
https://brainly.com/question/26974513
#SPJ4
________ scale is an actual number of purchases in a certain time period, dollars spent, miles traveled, number of children in the household, or years of college education.
Answers
Ratio scale is an actual number of purchases in a certain time period, dollars spent, miles traveled, number of children in the household, or years of college education.
The ratio scale is the highest form of measurement and has all the properties of the nominal, ordinal, and interval scales.
It has an absolute zero point and measurements that can be mathematically operated on.
Therefore, it is easy to calculate ratios and compare magnitudes between different things with ratio scales. The zero point implies that nothing is available in the variable.
As a result, comparisons with ratios are more precise. The ratio scale is the most useful of the four scales of measurement because it allows for more precise and standardized measurement with mathematical operations.
Therefore, Ratio scale is an actual number of purchases in a certain time period, dollars spent, miles traveled, number of children in the household, or years of college education.
Learn more about ratio scale here:
https://brainly.com/question/31315229
#SPJ11
Find the missing side lengths

Answers
Answer:
\( \sin(45) = \frac{o}{h} \\ 0.7 = \frac{x}{18 \sqrt{2} } \\ 0.7 \times 18 \sqrt{2} = x \\ 0.7 \times 25.45 = x \\ 17.8 = x\)
\( {x}^{2} + {y}^{2} =( 18 \sqrt{2} ) ^{2} \\ {17.8}^{2} + {y}^{2} = 648 \\ 316.84 + {y}^{2} = 648 \\ {y}^{2} = 648 - 316.84 \\ {y}^{2} = 331.16 \\ y = 18.19\)
I need help solving this practiceThe answer options for the three boxes are located at the bottom of the picture One answer option per box

Answers
To answer this question we will use the following trigonometric identity:
\(\sin^2\theta+\cos^2\theta=1.\)Solving the first equation for cosθ we get:
\(\begin{gathered} x-2=4\cos\theta+2-2, \\ x-2=4\cos\theta, \\ \frac{x-2}{4}=\frac{4\cos\theta}{4}, \\ \frac{x-2}{4}=\cos\theta. \end{gathered}\)Solving the second equation for sinθ we get:
\(\begin{gathered} y+5=2\sin\theta-5+5, \\ y+5=2\sin\theta, \\ \frac{y+5}{2}=\frac{2\sin\theta}{2} \\ \frac{y+5}{2}=\sin\theta. \end{gathered}\)Substituting
\(\cos\theta=\frac{x-2}{4}\text{ and }\sin\theta=\frac{y+5}{2}\)in the trigonometric identity we get:
\((\frac{x-2}{4})^2+(\frac{y+5}{2})^2=1.\)Simplifying the above result we get:
\(\frac{(x-2)^2}{16}+\frac{(y+5)^2}{4}=1\)Finally, recall that:
\(-1\leq\cos\theta\le1.\)Therefore:
\(\begin{gathered} -4+2\leq4\cos\theta+2\leq4+2, \\ -2\leq4\cos\theta+2\leq6. \end{gathered}\)Therefore x is on the interval:
\([-2,6].\)Answer:
\(\frac{(x-2)^2}{16}+\frac{(y+5)^2}{4}=1\)where x is on the interval
\([-2,6].\)
let a and b be integers. prove that if ab = 4, then (a – b)3 – 9(a – b) = 0.
Answers
Let \(\(a\)\) and \(\(b\)\) be integers such that \(\(ab = 4\)\). We want to prove that \(\((a - b)^3 - 9(a - b) = 0\).\)
Starting with the left side of the equation, we have:
\(\((a - b)^3 - 9(a - b)\)\)
Using the identity \(\((x - y)^3 = x^3 - 3x^2y + 3xy^2 - y^3\)\), we can expand the cube of the binomial \((a - b)\):
\(\(a^3 - 3a^2b + 3ab^2 - b^3 - 9(a - b)\)\)
Rearranging the terms, we have:
\(\(a^3 - b^3 - 3a^2b + 3ab^2 - 9a + 9b\)\)
Since \(\(ab = 4\)\), we can substitute \(\(4\)\) for \(\(ab\)\) in the equation:
\(\(a^3 - b^3 - 3a^2(4) + 3a(4^2) - 9a + 9b\)\)
Simplifying further, we get:
\(\(a^3 - b^3 - 12a^2 + 48a - 9a + 9b\)\)
Now, notice that \(\(a^3 - b^3\)\) can be factored as \(\((a - b)(a^2 + ab + b^2)\):\)
\(\((a - b)(a^2 + ab + b^2) - 12a^2 + 48a - 9a + 9b\)\)
Since \(\(ab = 4\)\), we can substitute \(\(4\)\) for \(\(ab\)\) in the equation:
\(\((a - b)(a^2 + 4 + b^2) - 12a^2 + 48a - 9a + 9b\)\)
Simplifying further, we get:
\(\((a - b)(a^2 + 4 + b^2) - 12a^2 + 39a + 9b\)\)
Now, we can observe that \(\(a^2 + 4 + b^2\)\) is always greater than or equal to \(\(0\)\) since it involves the sum of squares, which is non-negative.
Therefore, \(\((a - b)(a^2 + 4 + b^2) - 12a^2 + 39a + 9b\)\) will be equal to \(\(0\)\) if and only if \(\(a - b = 0\)\) since the expression \(\((a - b)(a^2 + 4 + b^2)\)\) will be equal to \(\(0\)\) only when \(\(a - b = 0\).\)
Hence, we have proved that if \(\(ab = 4\)\), then \(\((a - b)^3 - 9(a - b) = 0\).\)
To know more about satisfies visit-
brainly.com/question/16993710
#SPJ11
use the big-0 limit lemma to show that log(n) = o(n). then use the limit lemma to show that nx log n = o(nx 1) for any constant x.
Answers
The big-O limit lemma states that if f(n) = O(g(n)) as n approaches infinity, then lim n→∞ f(n)/g(n) = C for some constant C.
We must demonstrate that for any constant C > 0, there exists an N such that for all n > N, |log(n)| C*n in order to demonstrate that log(n) = o(n). Here's how to go about it:
For any constant C > 0, choose N = e^C. Then, for all n > N, we have:
log(n) < C
So, |log(n)| < C
And, |log(n)| < C*n
This means that log(n) = o(n), as required.
To show that n^x log(n) = o(n^x) for any constant x, we use the big-O limit lemma. Since log(n) = o(n), we have:
lim n→∞ (n^x log(n))/(n^x) = lim n→∞ log(n)/n^(x-1) = C for some constant C.
Since the limit of the right side is a finite constant, we can conclude that n^x log(n) = o(n^x), as required.
To know more about the big-0 limit lemma on brainly : brainly.com/question/15099298
#SPJ4
A contractor is required by a county planning department to submit anywhere from one to five forms (depending on the nature of the project) in applying for a building permit. Let r.v. X = the number of forms required of the next applicant. The probability that x forms are required is known to be proportional to x; that is, pX(x) = cx for x = 1, . . . , 5.
(a) (1 mark). What is the value of c?
(b) (1 mark). What is the probability that at most three forms are required?
(c) (1 mark). What is the probability that between two and four forms (inclusive) are required?
(d) (2 marks). Could pX(x) = x^2/50 for x = 1, . . . , 5 be a probability distribution of X? Explain.
Answers
The probability that x forms are required is known to be proportional to c = 1/15. c= 2/5 c= 3/5, c= 1.1
(a) Since the probabilities must sum to 1, we have:
pX(1) + pX(2) + pX(3) + pX(4) + pX(5) = c(1 + 2 + 3 + 4 + 5) = 15c
Therefore, c = 1/(1 + 2 + 3 + 4 + 5) = 1/15.
(b) The probability that at most three forms are required is:
P(X ≤ 3) = pX(1) + pX(2) + pX(3) = c(1 + 2 + 3) = 6c = 2/5.
(c) The probability that between two and four forms (inclusive) are required is:
P(2 ≤ X ≤ 4) = pX(2) + pX(3) + pX(4) = c(2 + 3 + 4) = 9c = 3/5.
(d) No, because the probabilities do not sum to 1:
Σ pX(x) from x = 1 to 5
= (1/50)(1 + 4 + 9 + 16 + 25)
= 55/50
= 1.1
Learn more about probabilities
https://brainly.com/question/30034780
#SPJ4
maggie is 16 years old and she is pregnant, what is the likely percentage that maggie will get pregnant again 2 years after the first baby's birth?
Answers
The likely percentage that Maggie will get pregnant again 2 years after the first baby's birth is not predictable as it depends on various factors.
It's important to note that individual circumstances can vary greatly, and predicting an exact percentage of Maggie's likelihood of getting pregnant again in 2 years isn't possible. However, some factors that may influence her chances include her age, contraceptive use, and personal choices.
Teenagers have a higher fertility rate, but using effective contraceptives and making informed decisions can reduce the likelihood of a subsequent pregnancy. It's crucial for Maggie to consult with a healthcare professional for personalized advice and support.
While research suggests that the chances of getting pregnant in the first year after childbirth are relatively high, the likelihood decreases over time, and after two years, it may be lower than the chances of getting pregnant for the first time.
To learn more about percentage, click here:
https://brainly.com/question/29306119
#SPJ11
PLEASE HELP ME I'M FAILING MATH-
Select the correct texts in the passage. Julian factored the expression
\( {2x}^{4} + {2x}^{3} - {x}^{2} - x\)
His work is shown. At which step did Julian make his first mistake, and which statement describes the mistake?
\(julian \: should \: have \:factored \:( {2x}^{2} - 1) \: as \: a \: difference \: of \: squares \: \\ \\ julian \: incorrectly \: factored \: - 1 \: from \: the \: second \: group \: of \: terms \: \\ \\ julian \: should \: have \: factored \: 2x \: from \: all \: terms \: instead \: of \: x \: \\ \\ julian \: incorrectly \: factored \: {2x}^{2} \: from \: the \: first \: group \: of \: terms\)
Answers
Julian factored the expression of 2x^4 + 2x³ - x²- x, the step 2 ( x (2x² (x + 1)) - 1(x − 1)) is wrong statement.
What is an expression?Expression in maths is defined as the collection of numbers variables and functions by using signs like addition, subtraction, multiplication, and division.
We have been given an expression as;
2\(x^{4}\) + 2x³ - x²- x
Step 1;
x(2x³ + 2x²- x − 1)
Step 2;
x (2x² (x + 1)) - 1(x − 1)
Step 3;
x²(2x²-1) (x + 1)(x - 1)
Hence, Julian incorrectly factored -1 from the second group of terms.
we can write the correct factored as;
x (2x²- 1))(x + 1)
Therefore, Julian factored the expression of 2\(x^{4}\) + 2x³ - x²- x, the step 2 ( x (2x² (x + 1)) - 1(x − 1)) is wrong statement.
To know more about an expression follow;
brainly.com/question/19876186
#SPJ5
HELPPP ASAP!!! WILL GIVE BRAINLYIST!!

Answers
Answer: The reflection is across x = 6.
Step-by-step explanation:
As you look at the reflection, you can see there is a shadowing with the two points on this graph. Point X1 is on (6, -1) and Point X is on (6, -7)
When looking at the graph, you can easily eliminate the x-axis and y-axis for an answer is because neither Point X1 nor Point X has a relationship to the axis.
Since the coordinates are precisely 6 units from each other, there is a reflection across x = 6.
Therefore, the reflection is across x = 6. Hope this helps!
-From a 5th Grade Honors Student
Sisters math question
5th
D16. The problem 7,291 – 19 is solved below using partial quotients. Identify what partial quotient was used in each step. Then, identify
your final quotient.
STEP 1
7291
- 5700
1591
- 1520
71
57
14
STEP 2
STEP 3
YOU CAN NOT MAKE ANY MORE GROUPS OF 19.
WHAT IS LEFT BECOMES YOUR REMAINDER
Answers
Answer:
How does one find use partial quotients for subration
Step-by-step explanation:
If a circle with a diameter of 4 inches rotates 1000°, what distance will any one spot on
its edge actually travel?
Answers
We first convert from degrees to radians multiplying by π/180:
θ = 1000° × π/180 = 17.45 rad
The radius is:
r = d/2 = 4 in /2 = 2 inch
So, The distance traveled is given by the product of the angle in radians and the radius. This is:
d = θr = (17.45 rad)(2 inch) = 34.9 inch
A continuous random variable is a random variable: A. that is derived from a random population B. whose values are countable C. that is determined by random probability D. that can assume any value in one or more intervals
Answers
Help please I am really struggling with this practice !

Answers
Answer:
The answer would be 71 because x = 9 so y = 71
Taylor drives 375 miles to get to his cousin's house. If the drive takes 15 hours, what is Taylor's rate of speed?
Answers
Answer:
25 mph
Step-by-step explanation:
The formula for speed is s = d/t.
s - speed
d - distance
t - time
For your problem, 375 mi is the distance and 15 hrs is the time. When you divide 375/15, you get an answer of 25. The unit of measure is miles per hour or mph. In the end, Taylor's speed is 25 mph. Hope this helps!!