State The Absolute value and the opposite of the number. -24, 8, 31, -17
Answers
24
8
31
17
absolute value with positive numbers are always positive if I remember correctly.
oooo and the opposite
24
-8
-31
and 17
Related Questions
Determine the value of x

Answers
Answer:
X=12
Step-by-step explanation:
70+25+9x-23=180°
95+9x-23=180°
9x+72=180°
9x=180°-72
9x=108°
x=12.
Find a positive number such that the sum of and is as small as possible. does this problem require optimization over an open interval or a closed interval? a. closed b. open
Answers
To find a positive number such that the sum of and is as small as possible, we need to use optimization. This problem requires optimization over a closed interval. The given problem is as follows, Let x be a positive number. Find a positive number such that the sum of and is as small as possible.
To find a positive number such that the sum of and is as small as possible, we need to use optimization. This problem requires optimization over a closed interval. The given problem is as follows, Let x be a positive number. Find a positive number such that the sum of and is as small as possible. So, we need to minimize the sum of and . Now, let's use calculus to find the minimum value of the sum.To find the minimum value, we have to find the derivative of the sum of and , i.e. f(x) with respect to x, which is given by f '(x) as shown below:
f '(x) = 1/x^2 - 1/(1-x)^2
We can see that this function is defined on the closed interval [0, 1]. The reason why we are using the closed interval is that x is a positive number, and both endpoints are included to ensure that we cover all positive numbers. Therefore, the problem requires optimization over a closed interval. This means that the minimum value exists and is achieved either at one of the endpoints of the interval or at a critical point in the interior of the interval.
To know more about positive number visit: https://brainly.com/question/17887499
#SPJ11
A bag contains 11 red M&Ms, 8 green M&Ms, and 6 blue M&Ms.What is the ratio of blue M&Ms to green M&Ms?
Answers
Answer:
The answer is 6/25 :8/25
I need help on a problem
Answers
b. Cannot be determined
Explanation:b. The triangle have one congruent angles and one congruent sides, this is not enough information to conclude that they are congruent triangles.
James sleeps for 8 hours in a day. what percentage of the day is james a. asleep b. awake
Answers
Step-by-step explanation:
asleep percentage :- ( 8h /24h ) 100 % = 33.33%
awake percentage :- ( 16h / 24h ) 100 % = 66.67%
Omega Instruments budgeted $430,000 per year to pay for special-order ceramic parts over the next 5 years. If the company expects the cost of the parts to increase uniformly according to an arithmetic gradient of $10.000 per year, what is the cost estimated to be in year 1 at an interest rate of 18% per year. The estimated cost is $
Answers
The estimated cost in year 1 is $526,400.
The initial cost is $430,000, and the cost increases uniformly according to an arithmetic gradient of $10,000 per year. At an interest rate of 18% per year, the estimated cost in year 1 is $526,400.
The arithmetic gradient is the fixed amount added to the previous value to arrive at the new value. An example of an arithmetic gradient is an investment or a payment that grows at a consistent rate. The annual increase in cost is $10,000, and this value remains constant throughout the five-year period.
The formula for arithmetic gradient is:
Arithmetic gradient = (Final cost - Initial cost) / (Number of years - 1)
The interest rate, or the cost of borrowing, is a percentage of the amount borrowed that must be repaid along with the principal amount. We will use the simple interest formula to calculate the estimated cost in year 1 since it is not stated otherwise.
Simple interest formula is:
I = Prt
Where: I = Interest amount
P = Principal amount
r = Rate of interest
t = Time period (in years)
Calculating the estimated cost in year 1 using simple interest:Initial cost = $430,000
Arithmetic gradient = $10,000
Number of years = 5
Final cost = Initial cost + Arithmetic gradient x (Number of years - 1)
Final cost = $430,000 + $10,000 x (5 - 1)
Final cost = $430,000 + $40,000
Final cost = $470,000
Principal amount = $470,000
Rate of interest = 18%
Time period = 1 yearI = PrtI = $470,000 x 0.18 x 1I = $84,600
Estimated cost in year 1 = Principal amount + Interest amount
Estimated cost in year 1 = $470,000 + $84,600
Estimated cost in year 1 = $554,600 ≈ $526,400 (rounded to the nearest dollar)
Therefore, the estimated cost in year 1 is $526,400.
Know more about estimated cost here,
https://brainly.com/question/33047951
#SPJ11
to calculate the cpi, the bureau of labor statistics uses
Answers
The CPI uses data from the Consumer Expenditure (CE) survey to determine the weights of the different categories of goods and services in the CPI. The CE survey collects data on the out-of-pocket expenses spent to acquire all consumer products and services.
CPI price data are collected via two surveys: one survey collects prices for commodities and services and the other survey collects prices for rent. The CPI survey collects about 94,000 prices per month to compute indexes for commodities and services.
The U.S. Consumer Price Index (CPI) is a collection of consumer price indices determined by the U.S. Bureau of Labor Statistics (BLS). To be specific, the BLS routinely calculates many distinctive CPIs that is practiced for several purposes.
Learn more about Bureau of Labor Statistics at:
https://brainly.com/question/25414516
#SPJ4
The given question is incomplete, So, take the similar question:
How does the Bureau of Labor Statistics calculate the CPI?
Combine like terms. -3 + 7x^2- 4x – 5 + 3x^2 – 2x
Answers
The expression is given as,
\(-3+7x^2-4x-5+3x^2-2x\)Rearranging the like terms,
\(7x^2+3x^2-4x-2x-5-3\)Like terms : Terms that have same power of variable.
Simplifying further,
\(10x^2-6x-8\)Thus the result of the given expression is,
\(10x^2-6x-8\)Answer:
-8 + 10x^2 - 6x
Step-by-step explanation:
(doesn’t have to be in this order)
1. Combine numbers with the x^2
-3 + 10x^2 - 4x - 5 - 2x
2. Combine regular numbers
-8 + 10x^2 - 4x - 2x
3. Combine numbers with the plain x
-8 + 10x^2 - 6x
What additional information is needed to show that ABC 2 ADEF by ASA?
A.AB≈DE
В.BC≈EF
с.AB ≈AC
D.AC≈DF

Answers
Answer:
AB≈DE
then, in triangle ABC&in triangle DEF
angle CAB =angle FDE
side AB= side DE
angle ABC= angle FED
So, triangle ATC≈ triangle DEF (A.S.A)
which graph of ordered pais shows a proportional relationship? i need help lol
Answers
What property of operations will be used to simplify the product of a binomial and trinomial? *
Answers
Answer:
Distributive property.
Step-by-step explanation:
A distributive property is a rule that states that, multiplying two factors such as a binomial and trinomial would give the same result as multiplying the sum of two addends by the other factor.
Hence, the distributive property is used to simplify the product of a binomial and trinomial.
For example, let's find the product of (2x + 4)(5x² + 3x + 10)
First of all, we would distribute trinomial into each of the term in the binomial.
2x(5x² + 3x + 10) + 4(5x² + 3x + 10)
Distributing the monomial into the trinomial, we have;
2x(5x²) + 2x(3x) + 2(10) + 4(5x²) + 4x(3x) + 4(10)
Expanding the bracket, we have;
10x³ + 6x² + 10 + 20x² + 12x² + 40
Collecting like terms, we have;
10x³ + (6x² + 20x² + 12x²) + 10 + 40
10x³ + 38x² + 50
Therefore, (2x + 4)(5x² + 3x + 10) = 10x³ + 38x² + 50
pleez help meeeeeeeeeeeeeeeeeee

Answers
Answer:
i believe its A and D hope this helps:)
Step-by-step explanation:
Combine the like terms to create an equivalent expression.
12r + 5 + 3 + 4r
Answers
Answer:
16r+8
Step-by-step explanation:
12r+4r+8=
16r+8
Please HELP im begging anyone Question 6 options:
The Edwards family spends $800 per month on groceries for their family. If this is 18% of their monthly budget, then what is their monthly budget?
Round to the nearest cent (hundredths place).
I suck at math so like yeah and i really need this good grade please
Answers
Answer:
$444.44
Step-by-step explanation:
Let the monthly budget of Edward family be $x.
-> 18% of x = 800
-> 0.18x = 800
-> x = 800/0.18
-> x = 444.44
Thus, the monthly budget of Edward family is $444.44.
A random variable is normally distributed with a mean of ? = 50 and a standard deviation of ? = 5.
a. What is the probability the random variable will assume a value between 45 and 55 (to 4 decimals)?
b. What is the probability the random variable will assume a value between 40 and 60 (to 4 decimals)?
Answers
a. There is a 0.6827 percent chance that the random variable will take on a value between 45 and 55. b. There is a 0.9545 percent chance that the random variable will take on a value between 40 and 60.
a. To find the probability that the random variable will assume a value between 45 and 55, we need to calculate the z-scores for each value and then use a standard normal distribution table or calculator.
The z-score for 45 is:
\(z = (45 - 50) / 5 = -1\)
The z-score for 55 is:
\(z = (55 - 50) / 5 = 1\)
Using a standard normal distribution table or calculator, we find the probability of the random variable assuming a value between 45 and 55 is:
P(-1 < Z < 1) = 0.6827 (to 4 decimals)
As a result, there is a 0.6827 percent chance that the random variable will take a value between 45 and 55.
b. To find the probability that the random variable will assume a value between 40 and 60, we again need to calculate the z-scores for each value and then use a standard normal distribution table or calculator.
The z-score for 40 is:
\(z = (40 - 50) / 5 = -2\)
The z-score for 60 is:
\(z = (60 - 50) / 5 = 2\)
Using a standard normal distribution table or calculator, we find the probability of the random variable assuming a value between 40 and 60 is:
P(-2 < Z < 2) = 0.9545 (to 4 decimals)
Hence, there is a 0.9545 percent chance that the random variable will take on a value between 40 and 60.
Learn more about probability here:
https://brainly.com/question/27223994
#SPJ4
How many factors does the algebraic expression 5xy have?
Answers
1 coefficient
Answer: 3 Factors
Step-by-step explanation:
a school has 2 computer labs.Each lab has 30 computers. A total of 6 computers in the school are not working. which experission can you use to find the number of working computers i the school
Answers
Answer:
30(2)-6
Step-by-step explanation:
30 computers in 2 labs minus the 6 broken computers.
Answer:
54
Step-by-step explanation:
2 times 30 =60 - 6 = 54
i think
Helena has taken out a $9,300 unsubsidized stafford loan to pay for her college education. she plans to graduate in four years. the loan has a duration of ten years and an interest rate of 6.4%, compounded monthly. by the time helena graduates, how much greater will the amount of interest capitalized be than the minimum amount that she could pay to prevent interest capitalization? round all dollar values to the nearest cent. a. $238.46 b. $496.00 c. $595.20 d. $324.33
Answers
Answer:
$324.33
Step-by-step explanation:
the answer is $324.33
The amount of interest capitalized is greater than the minimum amount that she could pay to prevent interest capitalization by; D: $324.33
What is the minimum Principal?We will use the formula: A = P(1 + r/n)^(nt)
Where:
A = final amount
P = initial principal ($9300)
r = interest rate (6.4% or 0.064)
n = number of times interest applied per time period
t = number of time period elapsed.
Thus;
9300(1 + 0.064/12)^(12*4) - 9300 = $2705.13
Also;
9300(0.064/12) * 4 * 12 = $2380.8
Answer = $2705.13 - $2380.8
Answer = $324.33
Read more about Principal amount at; https://brainly.com/question/25545513
help appreciated thanks

Answers
Answer:
No
Step-by-step explanation:
x=(b-5)/c≠(5-b)/c
supposedly
b=6
c=1
x=6-5/1=1
x=5-6/1= -1
1≠ -1
Answer:
No
Step-by-step explanation:
x = b - 5 / L equal to - (5 - b) / L
Are the two triangles similar? How do you know? (image attached)
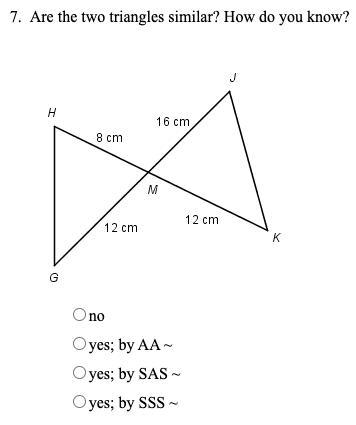
Answers
Answer:
no
Step-by-step explanation:
they're not same because no angles are mentioned and sides are diff too
Gonzalez Manufacturing borrowed $21000. Part of the money was borrowed at 10%, part at 12%, and part at 14%. The total amount borrowed at 10% and 12%
was twice the amount borrowed at 14%. Find the amount borrowed at each rate if the annual interest was $2580
How much money was borrowed at 10%?
How much money was borrowed at 12%?
How much money was borrowed at 14%?
Answers
Answer:
10% — $550012% — $700014% — $8500Step-by-step explanation:
You want to know the amount borrowed at 10%, 12%, and 14% if the total borrowed was $21000, the total interest was $2580, and the total of amounts borrowed at 10% and 14% was double the amount borrowed at 12%.
EquationsThe relations give rise to three equations. If we let x, y, z represent the respective amounts borrowed at 10%, 12%, and 14%, we have ...
x + y + z = 21000 . . . . . . total borrowed
0.10x +0.12y +0.14z = 2580 . . . . . . total interest
x + y = 2z . . . . . . . . . . . relationship between amounts
Writing the last equation as ...
x -2y +z = 0
we can formulate the problem as a matrix equation and use a solver to find the solution. We have done that in the attachment. It tells us the amounts borrowed are ...
10% — $550012% — $700014% — $8500__
Additional comment
Recognizing that the amount at 12% is 1/3 of the total, we can use that fact to rewrite the other two equations. The interest on the $7000 at 12% is $840, so we have ...
x + y = 140000.10x +0.14y = 1740These two equations have the solution shown above. (It is usually convenient to solve them by substituting for x in the second equation.)
<95141404393>

Find the missing side lengths...
Anybody know how to solve?

Answers
Answer:
No
Step-by-step explanation:
I don't know the answer
So 9 times 9 is 81 and 15 times 15 is 225. The new equation would be 81+X^2=225. To find X you would take 225 and subtract it from 81 to get 144. To get X you have to take the square root of 144 which is 12 so for #1 X will be 12. So for #2 you would take 6^2+X^2=10^2. The new equation is 36+X^2=100. You would do 100-36=64. 64=X^2. The square root of 64 is 8 so X would be 8. I hope I helped.
Find the measure of each angle indicated.
A D
A) 21°
C) 23°
E 25°
B) 80°
D) 20°

Answers
Let the missing Angle be " x "
We know that Measure of an exterior angle of a triangle is equal to sum of the opposite two interior angles,
that is :
x + 80° = 100°x = 100° - 80° x = 20°value of missing angle = 20°
The graph of a sinusoidal function intersects its midline at (0, 1) and then has a maximum point at
Write the formula of the function, where is entered in radians.
f(x) =

Answers
Answer:
f(x) = 4·sin(2/7x) +1
Step-by-step explanation:
The sinusoidal function y = a·sin(kx) +b will have cross its midline at (0, b), and a peak value of (x, y) = (π/(2k), a+b). We can use these facts to find the values of a, k, and b for the sinusoidal function.
__
midline(0, b) = (0, 1) ⇒ b = 1
peak value(7π/4, 5) = (π/(2k), a+1)
This gives rise to two equations:
7π/4 = π/(2k)
k = π/(2(7π/4)) = 2/7
and
a+1 = 5
a = 4
equationUsing the found values for the parameters of the function, we have ...
f(x) = 4·sin(2/7x) +1

Ali plans to buy 6 softballs and 3 soccer balls for the teen club. If he has a coupon for $8 off his purchase , how much will he pay for the balls?
Answers
Answer:
c=(6x+3y)-8
Step-by-step explanation:
Set up, but do not evaluate, an integral for the length of the curve.x = y + y45 ≤ y ≤ 6
Answers
To set up an integral for the length of the curve, we can use the formula:
length = ∫[a,b] √(1 + (dy/dx)²) dx
where a and b are the limits of integration.
In this case, we are given the curve x = y + y4, which can be rewritten as y = (x/(1+4))^(1/4) using algebraic manipulation.
Next, we can find the derivative of y with respect to x:
dy/dx = ((1/(1+4))^(1/4))/(4*(x/(1+4))^(3/4))
Substituting this into the formula for length, we get:
length = ∫[4, 65] √(1 + ((1/(1+4))^(1/4))/(4*(x/(1+4))^(3/4))²) dx
The formula for the length of a curve involves finding the integral of the square root of the sum of the squares of the derivatives of the curve with respect to x. This formula is derived from the Pythagorean theorem, where the length of a small segment of the curve is equal to the square root of the sum of the squares of its horizontal and vertical components.
we first need to rewrite the given curve in terms of y, since the formula requires the derivative of y with respect to x. We then find the derivative and substitute it into the formula for length.
It is important to note that we only set up the integral and did not evaluate it. Evaluating the integral would require either integration by substitution or numerical integration methods.
we can set up an integral for the length of the curve x = y + y4 by using the formula for length and finding the derivative of y with respect to x. We then substitute these into the formula and obtain an integral that can be evaluated using integration techniques.
To know more about integration visit:
https://brainly.com/question/31744185
#SPJ11
If X has an exponential (A) PDF, what is the PDF of W = X??
Previous question
Answers
The PDF of W = X², if X has an exponential distribution with parameter λ, is equal to fW(w) = (1/2)λ√w × \(e^{(-\lambda \sqrt{w} )}\) for w ≥ 0 and fW(w) = 0 for w < 0.
To find the probability density function (PDF) of the random variable W = X² when X has an exponential distribution with parameter λ,
Apply a transformation to the original PDF.
Let us denote the PDF of X as fX(x) and the PDF of W as fW(w). We want to find fW(w).
To begin, let us express W in terms of X,
W = X²
Now, find the PDF of W, which is the derivative of the cumulative distribution function (CDF) of W.
So, find the CDF of W first.
The CDF of W is ,
FW(w) = P(W ≤ w)
Substituting W = X², we have,
FW(w) = P(X² ≤ w)
To determine the probability of X² being less than or equal to w,
consider that X can take on both positive and negative values.
So, split the calculation into two cases,
First case,
X ≥ 0
In this case, X² ≤ w implies X ≤ √w, since X is non-negative.
Thus, we have,
FW(w) = P(X² ≤ w) = P(X ≤ √w)
Since X has an exponential distribution, its CDF is given by,
FX(x) = 1 -\(e^{(-\lambda x)}\) for x ≥ 0
for the case X ≥ 0, we have,
FW(w) = P(X ≤ √w) = FX(√w) = 1 -\(e^{(-\lambda \sqrt{w} )}\)
Second case,
X < 0
X² ≤ w implies X ≤ -√w, since X is negative.
However, for X < 0, X² is always non-negative.
The probability is always 0 in this case.
Combining both cases, we can write the CDF of W as,
FW(w) = 1 - \(e^{(-\lambda \sqrt{w} )}\) for w ≥ 0
FW(w) = 0 for w < 0
Finally, to find the PDF fW(w), we take the derivative of the CDF with respect to w,
fW(w) = d/dw [FW(w)]
Differentiating, we have,
fW(w) = (1/2)λ√w × \(e^{(-\lambda \sqrt{w} )}\) for w ≥ 0
fW(w) = 0 for w < 0
Therefore, the PDF of W = X², when X has an exponential distribution with parameter λ, is given by,
fW(w) = (1/2)λ√w × \(e^{(-\lambda \sqrt{w} )}\) for w ≥ 0
fW(w) = 0 for w < 0
learn more about exponential here
brainly.com/question/31422980
#SPJ4
The above question is incomplete, the complete question is:
If X has an exponential (λ) PDF, what is the PDF of W = X² ?
which was EAV-Secure Prove the opposite - i.e. if G is not a PRG, then 3.17 cannot be EAV-secure. Let G be a pseudorandom generator with expansion factor ℓ. Define a private-key encryption scheme for messages of length ℓ as follows: - Gen: on input 1n, choose uniform k∈{0,1}n and output it as the key. - Enc: on input a key k∈{0,1}n and a message m∈{0,1}ℓ(n), output the ciphertext c:=G(k)⊕m. - Dec: on input a key k∈{0,1}n and a ciphertext c∈{0,1}ℓ(n), output the message m:=G(k)⊕c. A private-key encryption scheme based on any pseudorandom generator. THEOREM 3.18 If G is a pseudorandom generator, then Construction 3.17 is a fixed-length private-key encryption scheme that has indistinguishable encryptions in the presence of an eavesdropper. PROOF Let Π denote Construction 3.17. We show that Π satisfies Definition 3.8. Namely, we show that for any probabilistic polynomial-time adversary A there is a negligible function negl such that Pr[PrivKA,Πeav(n)=1]≤21+neg∣(n)
Answers
To prove the opposite, we need to show that if G is not a pseudorandom generator (PRG), then Construction 3.17 cannot be EAV-secure.
Assume that G is not a PRG, which means it fails to expand the seed sufficiently. Let's suppose that G is computationally indistinguishable from a truly random function on its domain, but it does not meet the requirements of a PRG.
Now, consider the private-key encryption scheme Π described in Construction 3.17 using G as the pseudorandom generator. If G is not a PRG, it means that its output is not sufficiently pseudorandom and can potentially be distinguished from a random string.
Given this scenario, an adversary A could exploit the distinguishability of G's output and devise an attack to break the security of the encryption scheme Π. The adversary could potentially gain information about the plaintext by analyzing the ciphertext and the output of G.
Therefore, if G is not a PRG, it implies that Construction 3.17 cannot provide EAV-security, as it would be vulnerable to attacks by distinguishing the output of G from random strings. This contradicts Theorem 3.18, which states that if G is a PRG, then Construction 3.17 achieves indistinguishable encryptions.
Hence, by proving the opposite, we conclude that if G is not a PRG, then Construction 3.17 cannot be EAV-secure.
To know more about pseudorandom generator refer to-
https://brainly.com/question/33563626
#SPJ11
KTMN is a parallelogram . prove it .please help I need it by tomorrow no links please

Answers
Answer:
This is a paralleogram because it machtes the defintion ofa four-sided plane rectilinear figure with opposite sides parallel.
Step-by-step explanation:
Which of the following is the prime factored form of the lowest common denominator of 15/28-5/12?
Answers
Answer:
5/6
Step-by-step explanation:
15/28 - 5/12
LCM of 28 & 12 is 336
420 - 140
--------------
336
=280
--------
336
= 280/336
=5/6