Square oabc is drawn on a centimetre grid.o is (0,0) a is(3,0) b is(3,3) c is (0,3)write down how many invariants points there are on the perimeter of the square when oabc is translated by the vector (1 3)
Answers
There are 4 invariant points on the perimeter of the square when oabc is translated by the vector (1 3).
To find the invariant points on the perimeter of the square when oabc is translated by the vector (1 3), we need to apply this translation to each vertex of the square and see which ones remain on the square.
If we add the vector (1 3) to each vertex, we get:
o + (1 3) = (1 3)
a + (1 3) = (4 3)
b + (1 3) = (4 6)
c + (1 3) = (1 6)
Now we need to check which of these points are still on the square. We can see that points (1 3) and (4 3) are on two adjacent sides of the square, and points (1 6) and (4 6) are on the other two adjacent sides.
Therefore, there are 4 invariant points on the perimeter of the square when oabc is translated by the vector (1 3). These invariant points are the points where the sides of the original square intersect with the sides of the translated square.
To know more about invariant points refer here:
https://brainly.com/question/28565229#
#SPJ11
Related Questions
Help me on this please don’t know how to do it

Answers
Answer:
Step-by-step explanation:
formula of volume of cylinder is (\(\pi\)r2h)
= 22/7*7 square*3
= 22/7*49*3
= 462
we cancelled 7/49 we get the answer as 7 then multiplied by 3 we get the answer as 21 and then multiple 22*21 u will get 462
HELP WILL GIVE 20PTS PLEASE HELP ASAP

Answers
Answer:
hi, where's mt 20pts
Step-by-step explanation:
0.3
12+6+9+13=40
12/40 (or 3/10 simplified)
Thus, 0.3 as a decimal
Hope this helps!
let a and b be two disjoint events. under what conditions are they independent?
Answers
Disjoint events are events that cannot happen at the same time. Two events A and B are independent if the occurrence of A does not affect the probability of B happening, and vice versa. Mathematically, this can be written as P(A and B) = P(A)P(B).
In the case of disjoint events, P(A and B) = 0 because they cannot occur at the same time. Therefore, the condition for A and B to be independent is that either P(A) = 0 or P(B) = 0, since any non-zero probability for either event would make the product P(A)P(B) also non-zero.
Two disjoint events are independent if and only if at least one of them has zero probability.
To learn more about probability : brainly.com/question/32004014
#SPJ11
the cover charge for entering mandi's dance hall is $5. drinks are then $6 each. what equation, in point-slope form, will give the total cost for the cover charge and drinks?
Answers
The equation of the total cost for the cover charge and drinks in point-slope form is y = 6x + 5.
The point-slope form of a linear equation is given by -
\(y - y_1 = m(x- x_1)\)
where m is the slope and \((x_1, y_1)\) is a point on the line.
Here, the total cost for the cover charge and drinks can be represented by the equation y = mx + b, where y is the total cost, x is the number of drinks, m is the cost per drink, and b is the cost of the cover charge.
We know that the cover charge is $5 and drinks are $6 each, so, we can find the slope (m) of the equation by using the cost per drink which is m = 6.
We can also find the point \((x_1, y_1)\) by using the cover charge cost which is (0,5).
Therefore, the equation in point-slope form of the total cost for the cover charge and drinks will be -
y - 5 = 6(x-0)
y - 5 = 6x
y = 6x + 5
Where x is the number of drinks and y is the total cost i.e. cover charge + drinks.
Read more about the point-slope equation:
brainly.com/question/24907633
#SPJ4
Solve the inequality and SHOW ALL WORK Plz Help Now Due In 15 minutes
−(1+5x)−6(−1+5x)≤−65
Answers
\( - 1 - 5x + 6 - 30x \leqslant - 65\)
\( - 35x + 5 \leqslant - 65\)
Factoring -5
\( - 5(7x - 1) \leqslant - 65\)
Divided sides by -5
##############################
Point :
If the sides of an inequality are multiplied by or divided by a negative number, the direction of the inequality changes and returns.
##############################
\( \frac{ - 5}{ - 5}(7x - 1) \geqslant \frac{ - 65}{ - 5} \\ \)
\(7x - 1 \geqslant 13\)
Plus sides 1
\(7x - 1 + 1 \geqslant 13 + 1\)
\(7x \geqslant 14\)
Divided sides by 7
\( \frac{7}{7}x \geqslant \frac{14}{7} \\ \)
\(x \geqslant 2\)
Done ♥️♥️♥️♥️♥️
Let G be an undirected graph with n vertices. Let Δ(G) be the maximum degree of any vertex in G, δ(G) be the minimum degree of any vertex in G, and m be the number of edges in G. Prove that: [δ(G)*n]/2 <= m <= [Δ(G)*2]/2
Answers
The proven that [δ(G)*n]/2 <= m <= [Δ(G)*n]/2. Given: Let G be an undirected graph with n vertices.
Let Δ(G) be the maximum degree of any vertex in G, δ(G) be the minimum degree of any vertex in G, and m be the number of edges in G.Prove: [δ(G)*n]/2 <= m <= [Δ(G)*n]/2 Proving : [δ(G)*n]/2 <= m.
We know that, The sum of degrees of vertices of an undirected graph is equal to twice the number of edges.
Σ deg(V) = 2m Also, δ(G) <= deg(V) <= Δ(G)So, δ(G) <= Σ deg(V) /n <= Δ(G)δ(G)*n <= Σ deg(V) <= Δ(G)*n2m = Σ deg(V)≥ δ(G)*n and m ≥ [δ(G)*n]/2 Proving : m <= [Δ(G)*n]/2Also,δ(G) <= deg(V) <= Δ(G)δ(G)*n <= Σ deg(V) <= Δ(G)*n2m = Σ deg(V)So, m <= Σ deg(V) /2 <= Δ(G)*n /2and m <= [Δ(G)*n]/2
Therefore, we have proven that [δ(G)*n]/2 <= m <= [Δ(G)*n]/2.
To know more about undirected graph visit:
brainly.com/question/33359365
#SPJ11
(1 point) let r(t)=⟨t2,1−t,4t⟩. calculate the derivative of r(t)⋅a(t) at t=8, assuming that a(8)=⟨−8,−6,7⟩ and a′(8)=⟨4,8,−3⟩ ddt[r(t)⋅a(t)]|t=8
Answers
The derivative of r(t)⋅a(t) at t=8 is -126. To find the derivative of r(t)⋅a(t) at t=8, first, calculate the derivative of r(t) and then use the product rule.
The derivative of r(t) is r'(t) = ⟨2t, -1, 4⟩.
Now, use the product rule: d/dt[r(t)⋅a(t)] = r'(t)⋅a(t) + r(t)⋅a'(t)
At t=8, r(8) = ⟨64, -7, 32⟩, r'(8) = ⟨16, -1, 4⟩, a(8) = ⟨-8, -6, 7⟩, and a'(8) = ⟨4, 8, -3⟩.
Compute the dot products: r'(8)⋅a(8) = (16 * -8) + (-1 * -6) + (4 * 7) = -128 + 6 + 28 = -94
r(8)⋅a'(8) = (64 * 4) + (-7 * 8) + (32 * -3) = 256 - 56 - 96 = 104
Now add the two dot products: -94 + 104 = 10
So, d/dt[r(t)⋅a(t)]|t=8 = 10.
To calculate the derivative of r(t)⋅a(t), we need to use the product rule of differentiation.
r(t)⋅a(t) = ⟨t2,1−t,4t⟩ ⋅ ⟨−8,−6,7⟩ = -8t2 - 6(1-t) + 28t
So,
ddt[r(t)⋅a(t)] = ddt[-8t2 - 6(1-t) + 28t]
= -16t - 6 + 28
Now, we need to evaluate this derivative at t=8 and use the given value of a'(8).
ddt[r(t)⋅a(t)]|t=8 = -16(8) - 6 + 28 = -126
Therefore, the derivative of r(t)⋅a(t) at t=8 is -126.
Learn more about product rule here: brainly.com/question/30117847
#SPJ11
i really need help with this fast!!

Answers
it should be y= 3/2x + 2
The point P(3, -4) lies on the curve y = 4/(2 - x). (a) If Q is the point (x, 4/(2 - x)), use your calculator to find the slope mPQ of the secant line PQ (correct to six decimal places) for the following values of x. (i) 2.9 mPQ = (ii) 2.99 mPQ = (iii) 2.999 mPQ = (iv) 2.9999 mPQ = (v) 3.1 mPQ = (vi) 3.01 mPQ = (vii) 3.001 mPQ = (viii) 3.0001 mPQ = (b) Using the results of part (a), guess the value of the slope m of the tangent line to the curve at P(3, -4). m = (c) Using the slope from part (b), find an equation of the tangent line to the curve at P(3, -4).
Answers
y=38x-118
a) To find the slope of PQ, we have to find the slope of the secant line. It can be found using the formula (y2−y1)/(x2−x1). We know that the point P (3, −4) lies on the curve y=4/(2−x). Therefore, the coordinates of P can be substituted in the above equation to obtain the slope of the tangent at the point P.
The coordinates of point Q can be found using the given equation of the curve as shown below:
y = 4/(2 - x)
For x = 2.9, y = 4/(2 - 2.9) = −40. The coordinates of point Q for other values of x can be computed similarly. Therefore, the coordinates of Q for the given values of x are given below:
(2.9, -40)
(2.99, -400)
(2.999, -4000)
(2.9999, -40000)
(3.1, 40)
(3.01, 400)
(3.001, 4000)
(3.0001, 40000)
The slope of PQ for each of the above points can be found using the formula mentioned earlier. Therefore, the slope of PQ for the given values of x are given below:
(i) mPQ = (−40−(−4))/(2.9−3) = 38
(ii) mPQ = (−400−(−4))/(2.99−3) = 38.006944
(iii) mPQ = (−4000−(−4))/(2.999−3) = 38.000694
(iv) mPQ = (−40000−(−4))/(2.9999−3) = 38.000069
(v) mPQ = (40−(−4))/(3.1−3) = 44
(vi) mPQ = (400−(−4))/(3.01−3) = 388.888889
(vii) mPQ = (4000−(−4))/(3.001−3) = 3888.888889
(viii) mPQ = (40000−(−4))/(3.0001−3) = 38888.888889
b) From the values of slope found in part (a), we can guess the value of slope m of the tangent at P (3, −4) to the curve y=4/(2−x) as shown below.
The slope of PQ is computed for values of x near 3, and it is observed that the slope converges to 38. Therefore, the value of the slope of the tangent at point P (3, −4) is 38.
c) Using the slope found in part (b), we can find the equation of the tangent line at point P (3, −4).
The equation of the tangent line to the curve y = 4/(2 - x) at the point P (3, −4) with slope m = 38 is given below:
y − (−4) = m(x − 3)
⇒ y + 4 = 38(x − 3)
⇒ y = 38x − 118
Therefore, the equation of the tangent line is y = 38x - 118.
To learn more about secant line, refer below:
https://brainly.com/question/31124520
#SPJ11
The degrees of freedom for two dependent groups is number of paired differences-1. True False
Answers
True. This is because the paired differences are not independent, as each difference is calculated from the same set of observations or individuals.
The statement is true. When dealing with dependent or paired groups, such as in a paired t-test or a repeated measures design, the degrees of freedom are determined by the number of paired differences minus 1.
This is because the paired differences are not independent observations, as each difference is calculated from the same set of individuals or matched pairs.
By subtracting 1 from the number of paired differences, we account for the loss of one degree of freedom due to the dependency between the paired values. The degrees of freedom play a crucial role in determining the critical values and conducting statistical tests for dependent group analyses.
Learn more about paired differences
brainly.com/question/31686880
#SPJ11
suppose components , , and operate independently, in the system shown in the figure. assume that all the components in the system start operating at the same time and a component does not work again once it fails. the probability of functioning of each of the components is . the entire system works (i.e., operate without failure) if or works and or works. find the probability that the entire system works (round off to second decimal place).
Answers
The probability that the entire system works is approximately 0.52, rounded off to the second decimal place.
What is probability?
Probability is the study of the chances of occurrence of a result, which are obtained by the ratio between favorable cases and possible cases.
Let A, B, and C represent the events that components A, B, and C work, respectively. Then, the probability that a component works is given as P(A) = P(B) = P(C) = p.
The probability that the entire system works is the probability that either A and B work and C does not, or A and C work and B does not. This can be expressed as:
P(system works) = P((A and B and C') or (A and B' and C))
Using the distributive property of probability, we can rewrite this as:
P(system works) = P(A and B and C') + P(A and B' and C)
Since the components work independently, we can apply the product rule of probability to each term:
P(system works) = P(A) * P(B) * (1 - P(C)) + P(A) * (1 - P(B)) * P(C)
Substituting P(A) = P(B) = P(C) = p, we get:
P(system works) = p² * (1 - p) + p * (1 - p)²
Simplifying this expression, we get:
P(system works) = p * (2p - 3p² + 1)
Substituting the given value of p, we get:
P(system works) = 0.8 * (20.8 - 30.8² + 1) ≈ 0.52
Therefore, the probability that the entire system works is approximately 0.52, rounded off to the second decimal place.
To know more about probability visit :
https://brainly.com/question/13604758
#SPJ1
bacteria in a cetain culture increase at a rate proportional to the number present. if the number of bacteria doubles in three hours, in how many hours will the number of bacteria triple?
Answers
Since the rate of bacteria growth is proportional to the number present, we can express this relationship using a differential equation:
dN/dt = kN,
where N is the number of bacteria, t is the time, and k is the constant of proportionality.
Given that the number of bacteria doubles in three hours, we can write:
dN/dt = kN,
dN/N = k dt.
To solve this equation, we integrate both sides:
∫ dN/N = ∫ k dt,
ln(N) = kt + C,
where C is the constant of integration.
Now, let's consider the specific conditions. When the number of bacteria doubles, N/N0 = 2, where N0 is the initial number of bacteria.
ln(2) = k(3) + C,
C = ln(2) - 3k.
Now, let's find the time it takes for the number of bacteria to triple, which means N/N0 = 3:
ln(3) = k(t) + ln(2) - 3k,
ln(3) - ln(2) = k(t) - 3k,
ln(3/2) = k(t - 3),
t - 3 = (ln(3/2))/k,
t = (ln(3/2))/k + 3.
Therefore, in how many hours will the number of bacteria triple is given by (ln(3/2))/k + 3. The value of k depends on the specific growth rate of the bacteria in the culture.
To learn more about Differential equation - brainly.com/question/25731911
#SPJ11
Find all the solutions to \[\frac{x+4}{x+5} = \frac{x-5}{2x}.\]\(Find all the solutions to\[\frac{x+4}{x+5} = \frac{x-5}{2x}.\]\)
Answers
Answer:
x = -4 + 3 i or x = -4 - 3 i
Step-by-step explanation:
Solve for x:
(x + 4)/(x + 5) = (x - 5)/(2 x)
Hint: | Multiply both sides by a polynomial to clear fractions.
Cross multiply:
2 x (x + 4) = (x - 5) (x + 5)
Hint: | Write the quadratic polynomial on the left hand side in standard form.
Expand out terms of the left hand side:
2 x^2 + 8 x = (x - 5) (x + 5)
Hint: | Write the quadratic polynomial on the right hand side in standard form.
Expand out terms of the right hand side:
2 x^2 + 8 x = x^2 - 25
Hint: | Move everything to the left hand side.
Subtract x^2 - 25 from both sides:
x^2 + 8 x + 25 = 0
Hint: | Using the quadratic formula, solve for x.
x = (-8 ± sqrt(8^2 - 4×25))/2 = (-8 ± sqrt(64 - 100))/2 = (-8 ± sqrt(-36))/2:
x = (-8 + sqrt(-36))/2 or x = (-8 - sqrt(-36))/2
Hint: | Express sqrt(-36) in terms of i.
sqrt(-36) = sqrt(-1) sqrt(36) = i sqrt(36):
x = (-8 + i sqrt(36))/2 or x = (-8 - i sqrt(36))/2
Hint: | Simplify radicals.
sqrt(36) = sqrt(4×9) = sqrt(2^2×3^2) = 2×3 = 6:
x = (-8 + i×6)/2 or x = (-8 - i×6)/2
Hint: | Factor the greatest common divisor (gcd) of -8, 6 i and 2 from -8 + 6 i.
Factor 2 from -8 + 6 i giving -8 + 6 i:
x = 1/2-8 + 6 i or x = (-8 - 6 i)/2
Hint: | Cancel common terms in the numerator and denominator.
(-8 + 6 i)/2 = -4 + 3 i:
x = -4 + 3 i or x = (-8 - 6 i)/2
Hint: | Factor the greatest common divisor (gcd) of -8, -6 i and 2 from -8 - 6 i.
Factor 2 from -8 - 6 i giving -8 - 6 i:
x = -4 + 3 i or x = 1/2-8 - 6 i
Hint: | Cancel common terms in the numerator and denominator.
(-8 - 6 i)/2 = -4 - 3 i:
Answer: x = -4 + 3 i or x = -4 - 3 i
How do you find the area of a Pentagon with an apothem of 10mm?
Answers
The calculated area of the pentagon is 288.50 mm² if one of the sides of the apothem of 10mm.
Length of apothem = 10mm
The formula used to find the area of a pentagon is:
Area = (1/2) × apothem × perimeter
Here the perimeter is the unknown term, so we need to calculate the perimeter of the Pentagon. The perimeter of a pentagon is calculated by the product of 5 times the length.
Let us assume that the length of one side of the Pentagon = s
The side of the Pentagon is:
s = (2 × apothem) / tan(180° / 5)
s = (2 × 10) / tan(36°)
s = 11.54 mm
Perimeter = 5*s
Perimeter = 5 * 11.54 = 57.70 mm
Now, the area of the Pentagon is:
Area = (1/2) × apothem × perimeter
Area = (1/2) × 10 × 57.70 = 288.50 mm²
Therefore, we can conclude that area of the pentagon is 288.50 mm².
To learn more about the Area of Pentagon
https://brainly.com/question/27565523
#SPJ1
Spoorthi plants 5 tree seedlings for every 3 that Hammad plants. If Hammad planted 6 trees in a minute, how many did Spoorthi plant?
Answers
10 plants
Explanation:
5 plants for every 3 plants
3 x 2 = 6
5 x 2 = 10
sarah is playing a game in which she rolls a number cube 20 times the results are recorded in the chart below. what is the experimental probability of rolling a 1 or a 2? answers 0.3, 0.45, 0.65, 1.25.
Answers
The experimental probability of rolling a 1 or a 2 is 0.2.
Hence, Option A is correct.
We know that,
The experimental probability of an event is defined as the number of times the event occurred divided by the total number of trials.
In this case,
The event is rolling a 1 or a 3,
Which occurred ⇒ 3 + 1
= 4 times.
Given that there are total number of trials = 20.
Therefore,
The experimental probability of rolling a 1 or a 3 = 4/20,
= 1/5
= 0.2
Hence, the required probability is 0.2.
Learn more about the probability visit:
https://brainly.com/question/13604758
#SPJ1
The complete question is:
Sarah is playing a game in which she rolls a number cube 20 times. The results are recorded in the chart below. What is the experimental probability of rolling a 1 or a 3?
Number on cube:1,2,3,4,5,6
Number of times event occurs:3,6,1,5,3,2
A.0.2
B.0.3
C.0.6
D.0.83
-17.9 as a mixed number.
Answers
Answer:
-17 9/10
Step-by-step explanation:
Clarissa took a job through an employment agency. The job pay $395 per week.Clarrisa must pay a fee to the employment agency. The fee is 20% of her first fourweeks pay. How much money must Clarrisa pay the agency?
Answers
Given Data:
The salary of Clarissa is : $395 per week
The total amount Clarissa own the employment agency is 20% of the 4 weeks salery.
The total salary of employment agency in four week is,
\(395\times4=1580\)Clarissa earn $1580 in her first four week.
The 20% of the $1580 is the amount Clarissa owns the agency.
The 20% of the $1580 is,
\(\begin{gathered} 1580\times\frac{20}{100}=1580\times0.2 \\ =316 \end{gathered}\)Thus, Clarissa has to pay $316 to the employment agency.
question 1 parent functions graph

Answers
Answer:
c. Square Root
If you want me to explain, let me know!
Consider a voted koon structure. The voting can be specified in two different ways:
– As the number k out of the n components that need to function for the system to function.
– As the number k of the n components that need to fail to cause system failure.
In the first case, we often write koon:G (for "good") and in the second case, we write koon:F (for failed).
(a) Determine the number x such that a 2004:G structure corresponds to a xoo4:F structure.
(b) Determine the number x such that a koon:G structure corresponds to a xoon:F structure.
Answers
In reliability engineering, systems can be represented in terms of components that need to function or fail for the system to function or fail.
The notation koon:G represents the number of components that need to function for the system to function, while koon:F represents the number of components that need to fail to cause system failure. The goal is to determine the value of x in different scenarios to understand the system's behavior.
(a) To find the number x such that a 2004:G structure corresponds to a xoo4:F structure, we need to consider that the total number of components is n = 4. In a 2004:G structure, all four components need to function for the system to function. Therefore, we have koon:G = 4. In an xoo4:F structure, all components except x need to fail for the system to fail. In this case, we have koon:F = n - x = 4 - x.
Equating the two expressions, we get 4 - x = 4, which implies x = 0. Therefore, a 2004:G structure corresponds to a 0400:F structure.
(b) To determine the number x such that a koon:G structure corresponds to a xoon:F structure, we have k components that need to function for the system to function. Therefore, koon:G = k. In an xoon:F structure, x components need to fail for the system to fail.
Hence, we have koon:F = x. Equating the two expressions, we get k = x. Therefore, a koon:G structure corresponds to a koon:F structure, where the number of components needed to function for the system to function is the same as the number of components needed to fail for the system to fail.
By understanding these representations, we can analyze system reliability and determine the criticality of individual components within a larger system. This information is valuable in designing robust and resilient systems, as well as identifying potential points of failure and implementing appropriate redundancy or mitigation strategies.
Learn more about function here: brainly.com/question/30721594
#SPJ11
Complete the expression so it forms a perfect-square trinomial.
x² - 5x +
✔ 25/4
x² +
x + 49
Answers
Answer:
Second question in Assignment = A) 14
Step-by-step explanation:
x^2 = 14x +49
Answer: 14
Step-by-step explanation:
The first one is 25/4 then 14
Based on information from a large insurance company, 68% of all damage liability claims are made by single people under the age of 25. A random sample of 53 claims showed that 41 were made by single people under the age of 25. Does this indicate that the insurance claims of single people under the age of 25 is higher than the national percent reported by the large insurance company? State the null and alternate hypothesis.
Answers
No, it doesn't show that single individuals under the age of 25 have more insurance claims than the nationwide percent reported by the big insurance firm.
Hypothesis
Null hypothesis : H0: p = 0.68
Alternative hypothesis : Ha: p > 0.68
A random sample of 53 claims showed that 41 were made by single people under the age of 25.
Thus; p^ = 41/53 = 0.7736
The test statistic is
z = (p^ - p_o)/√(p_o(1 - p_o)/n)
z = (0.7736 - 0.68)/√(0.68(1 - 0.68)/41)
z = 0.0936/0.07285
z = 1.28
The p-value from z-score calculator, using z = 1.28, one tail hypothesis and significance level of 0.05,we have;
P(z > 1.28) = 0.100273
The p-value gotten is greater than the significance value and so we fail to reject the null hypothesis and conclude that there is insufficient evidence to support the claim.
To learn more about null hypothesis
https://brainly.com/question/17083644
#SPJ4
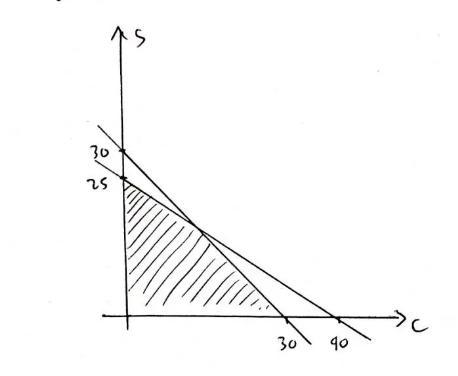
Alfred is picking up chicken and steak to grill at a party
later that day. He has $60 to spend on the 30 pounds of
meat he needs for the party. The chicken is $1.50 per lb,
and the steak is $2.40 per lb.
Which graph models this situation, where cis pounds of
chicken, and s is pounds of steak?
Answers
Answer:
The graph should look like the one below.
Step-by-step explanation:
C is lbs of chicken
S is pounds of steak
Alfred spent 30 pounds of meat for the party:
c + s \(\leq\) 30
Alfred spend $60 on the 30 lbs of meat.
The chicken is $1.50 per pound and the steak is $2.40 per lb then
1.5c + 2.50 \(\leq\) 60
0.5c + 0.85 \(\leq\) 20
The linear inequalities system that models situation is:
0.5c + 0.85 \(\leq\) 20
c + s \(\leq\) 30
c \(\geq\) 0
s \(\geq\) 0
The Graph:
answer the following questions

Answers
Answer:
A) Even Numbers and Odd Numbers
Step-by-step explanation:
find f(t). ℒ−1 s (s + 1)2
Answers
The function f(t) corresponding to the Laplace transform ℋ(f(t)) = ℋ{s(t)} is:
f(t) = u(t) + 2te^(-t) + t^2/2 u(t)
To find f(t) from the Laplace transform ℋ(f(t)), we need to apply the inverse Laplace transform ℒ⁻¹ to ℋ(f(t)).
Given ℋ(f(t)) = ℋ{s(t)}, we have:
ℒ⁻¹{ℋ(s(t))} = ℒ⁻¹{ℋ[(s + 1)²/s]} = ℒ⁻¹{ℋ[s/s] + ℋ[2s/(s+1)²] + ℋ[1/(s+1)²]}
Using the properties of Laplace transforms and taking the inverse Laplace transforms, we get:
f(t) = u(t) + 2te^(-t) + t^2/2 u(t)
where u(t) is the unit step function.
Therefore, the function f(t) corresponding to the Laplace transform ℋ(f(t)) = ℋ{s(t)} is:
f(t) = u(t) + 2te^(-t) + t^2/2 u(t)
Learn more about Laplace transform here:
https://brainly.com/question/1597221
#SPJ11
What is the value of x in the equation 0.3x = 12?
Answers
Answer:
You divide 0.3 by 12 if you don’t want a decimal do it the other way around the answer is x=40
Step-by-step explanation:
The value of x that satisfies the equation 0.3x = 12 is 40.
We have,
To find the value of x in the equation 0.3x = 12, we need to isolate x on one side of the equation.
We can do this by dividing both sides of the equation by 0.3, which will cancel out the coefficient of x on the left side:
(0.3x) / 0.3 = 12 / 0.3
Simplifying this equation gives:
x = 40
Thus,
The value of x that satisfies the equation 0.3x = 12 is 40.
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ6
• 1.Find the scale factor of a blueprint if the scale is 3 inches = 6 feet. A. 1/2 B. 1/24 C. 1/3 D. 1/72
Answers
Answer:
B. 1/24
Step-by-step explanation:
Given: 3 inches = 6 feet
Convert 6 feet into inches.
6 feet = 72 inches
3/72. Simplying it, you get 1/24
A school band performs a spring concert for a crowd of 600 people The revenue for the concert is $3150. There are 150 more adults at the concert than students. Students- $3 Adults- $7 Children under 12- $2
How many of each type ticket are sold?
Answers
Answer:
Number of adults = 350
Number of students = 200
Number of Children under 12 = 50
Step-by-step explanation:
Let
Number of adults = x
Number of students = y
Number of Children under 12 = z
Cost of each ticket
Students = $3
Adults = $7
Children under 12 = $2
Total crowd at the concert = 600
Total revenue = $3,150
There are 150 more adults at the concert than students.
That is, adults = y + 150
The equations
x + y + z = 600
7x + 3y + 2z = 3,150
Recall,
x = y + 150
y + 150 + y + z = 600
7(y + 150) + 3y + 2z = 3,150
2y + z + 150 = 600
7y + 1050 + 3y + 2z = 3,150
2y + z = 600 - 150
10y + 2z = 3150 - 1050
2y + z = 450 (1)
10y + 2z = 2,100 (2)
Multiply (1) by 2
4y + 2z = 900 (3)
10y + 2z = 2,100 (2)
Subtract (3) from (2)
10y - 4y = 2100 - 900
6y = 1200
Divide both sides by 6
y = 1200/6
= 200
Substitute the value of y into (1)
2y + z = 450
2(200) + z = 450
400 + z = 450
z = 450 - 400
= 50
z = 50
Substitute value of y into
x = y + 150
x = 200 + 150
= 350
x = 350
Therefore,
Number of adults = 350
Number of students = 200
Number of Children under 12 = 50
Round 452,489 to the nearest thousand.
O 500,000
0 453,000
450.000
452.000
Answers
The cost(c)of chicken varies directly as its weigth(w)equation
Answers
Answer:
\(c = kw\)
Step-by-step explanation:
Given
c varies directly as w
Required
Write the equation
c varies directly as w.
Mathematically, this is represented as:
\(c\ \alpha\ w\)
Convert to equation.
\(c = kw\)
Where k is the constant of variation