Answers
$92.92
Related Questions
Use the table to write a linear function that relates y to x .
y=

Answers
Answer:
y= -1/4x
Step-by-step explanation:
1. What are the opposite and absolute value of:
a) 7.2 ____,____ b) -3.5 ____, ____ c) 5 ½ ____,____
Answers
Answer:
a) 7.2, -7.2, 7.2
b) -3.5, 3.5, 3.5
c) 5 1/2, -5 1/2, 5 1/2
Step-by-step explanation:
The opposite number of a value is the number that adds to it to make zero. To find the opposite of a number you need to switch the sign, either from positive to negative or vice versa. The absolute value of a number is the distance from zero it is. Since distance cannot be negative you just need to take the number and make it positive.
Mr. Yang asked the 25 students in his class to vote for their favorite kind of candy. 20 students voted for chocolate. What percent of the students voted for chocolate?
Answers
Answer:
80%
Step-by-step explanation:
20/25 = 4/5 = 80/100 = 80%
80%
20 ÷ 25 · 100 = 80
Have a luvely day!
Guided Practice
Write an equation for the line that is perpendicular to the given line and that passes through the given point.
4x – 2y = 9; (8, –2)
A.
y=−1/2x−9/2
B.
y=1/2x+2
C.
y=−1/2x+2
Answers
Answer:
C.
y=−1/2x+2
Step-by-step explanation:
Find the negative reciprocal of the slope of the original line and use the point-slope formula y − y 1 = m ( x − x 1 ) to find the line perpendicular to 4 x − 2 y = 9 .
y = − 1 /2 x + 2
Find the prime factorization of 234.
Answers
Answer:2^1 × 3^2 × 13^1
Step-by-step explanation:
What is the answer pleaseee

Answers
Answer: 803.84cm3
Step-by-step explanation:
The formula for finding the volume of a cylinder is πr2h.
In other words, the area of the top face's circle times the height.
To find the circle's area, we first find the radius of the circle. Since the diameter is 8cm, we divide by 2 to get the radius, which is 4cm.
4cm squared is 4cm x 4cm, which is 16cm. 16cm times 3.14 is 50.24cm squared.
Now, we have the area of the circle. 50.24cm squared!
The height is 16cm, so to find the cylinder, we times the area of the circle by the height of the cylinder! So,
16cm x 50.24cm squared = 803.84cm cubed.
The volume of the can of soup is 803.84cm cubed.
27,813 students took the ACET this year. If only 2,836 students were admitted into the Ateneo among those students, what is the Ateneo’s acceptance rate? a. 7.5% b. 10.2% c. 13.4% d. 9.0%
Answers
If only 2,836 students were admitted into the Ateneo among 27,813 students, who took the ACET this year, the Ateneo’s acceptance rate is b. 10.2%.
How the rate is determined:The rate is the ratio of one value, expression, measurement, or quantity compared to another.
The rate represents the quotient of the numerator and the denominator.
The rate is expressed as a percentage by multiplication with 100.
The number of students who took the ACET this year = 27,813
The number of students who were admitted into the Ateneo = 2,836
The percentage or rate admitted = 10.19667% (2,836 ÷ 27,813 × 100)
= 10.2%
Thus, we can conclude that the acceptance rate or percentage is Option B.
Learn more about determining the percentage at https://brainly.com/question/24877689.
#SPJ1
What is the solution to √7x-4 = 2√x ?

Answers
Answer:
B
Step-by-step explanation:
take square on both sides,
7x-4 = 4x
so, x = 4/3
To avoid calculating difficult probabilities by hand, use aA. stimulationOB. simulcastOC. simulationD. stimulusReset SelectionNextto estimate the probability.

Answers
When probabilities are tedious, the method of of using hand is likely to produce errors. We can use simulation in this case. Thus, the correct option is
Find the center and radius of the circle represented by the equation below.

Answers
Answer:
centre = (5, - 6 ) , radius = 7
Step-by-step explanation:
the equation of a circle in standard form is
(x - h)² + (y - k)² = r²
where (h, k ) are the coordinates of the centre and r is the radius
given
x² + y² - 10x + 12y + 12 = 0 ( subtract 12 from both sides )
x² + y² - 10x + 12y = - 12 ( collect terms in x/ y )
x² - 10x + y² + 12y = - 12
using the method of completing the square
add ( half the coefficient of the x/ y terms )² to both sides
x² + 2(- 5)x + 25 + y² + 2(6)y + 36 = - 12 + 25 + 36
(x - 5)² + (y + 6)² = 49 = 7² ← in standard form
with centre (5, - 6 ) and radius = 7
Answer:
Center = (5, -6)
Radius = 7
Step-by-step explanation:
To find the center and the radius of the circle represented by the given equation, rewrite the equation in standard form by completing the square.
To complete the square, begin by moving the constant to the right side of the equation and collecting like terms on the left side of the equation:
\(x^2-10x+y^2+12y=-12\)
Add the square of half the coefficient of the term in x and the term in y to both sides of the equation:
\(x^2-10x+\left(\dfrac{-10}{2}\right)^2+y^2+12y+\left(\dfrac{12}{2}\right)^2=-12+\left(\dfrac{-10}{2}\right)^2+\left(\dfrac{12}{2}\right)^2\)
Simplify:
\(x^2-10x+(-5)^2+y^2+12y+(6)^2=-12+(-5)^2+(6)^2\)
\(x^2-10x+25+y^2+12y+36=-12+25+36\)
\(x^2-10x+25+y^2+12y+36=49\)
Factor the perfect square trinomials on the left side:
\((x-5)^2+(y+6)^2=49\)
The standard equation of a circle is:
\(\boxed{(x-h)^2+(y-k)^2=r^2}\)
where:
(h, k) is the center.r is the radius.Comparing this with the rewritten given equation, we get
\(h = 5\)\(k = -6\)\(r^2 = 49 \implies r=7\)Therefore, the center of the circle is (5, -6) and its radius is r = 7.
A researcher is interested in testing to determine if the mean price of a casual lunch is different in the city than it is in the suburbs. The null hypothesis is that there is no difference in the population means (i.e. the difference is zero). The alternative hypothesis is that there is a difference (i.e. the difference is not equal to zero). He randomly selects a sample of 9 lunch tickets from the city population resulting in a mean of $14.30 and a standard deviation of $3.40. He randomly selects a sample of 14 lunch tickets from the suburban population resulting in a mean of $11.80 and a standard deviation $2.90. He is using an alpha value of .10 to conduct this test. Assuming that the populations are normally distributed and that the population variances are approximately equal, the degrees of freedom for this problem are _______.
Answers
Answer:
The degrees of freedom for this problem are 21
Step-by-step explanation:
Degrees of freedom:
When testing an hypothesis involving two samples, the number of degrees of freedom is given by:
\(df = n_1 + n_2 - 2\)
In which \(n_1\) is the size of the first sample and \(n_2\) is the sample of the second sample.
In this question:
Samples of 9 and 14, so \(n_1 = 9, n_2 = 14\)
The degrees of freedom for this problem are
\(df = n_1 + n_2 - 2\)
\(df = 9 + 14 - 2 = 21\)
The degrees of freedom for this problem are 21
The required degree of freedom is 21.
Given that,
He randomly selects a sample of 9 lunch tickets from the city population resulting in a mean of $14.30 and a standard deviation of $3.40.
He randomly selects a sample of 14 lunch tickets from the suburban population resulting in a mean of $11.80 and a standard deviation $2.90.
He is using an alpha value of .10 to conduct this test.
We have to find,
The degrees of freedom for this problem are.
According to the question,
Degrees of freedom refers to the maximum number of logically independent values, which are values that have the freedom to vary, in the data sample.
Degrees of freedom are commonly discussed in relation to various forms of hypothesis testing in statistics, such as a chi-square.
When testing an hypothesis involving two samples, the number of degrees of freedom is given by,
\(Degree \ of \ freedom = n_1+n_2-2\)
Where, \(n_1\) is the size of the first sample and \(n_2\) is the sample of the second sample.
\(n_1 = 9 \ and\ n_2 = 14\)
Therefore,
\(Degree \ of \ freedom = 9+14-2\\\\Degree \ of \ freedom = 21\)
Hence, The required degree of freedom is 21.
To know more about Degree of Freedom click the link given below.
https://brainly.com/question/23452965
A certain manufacturing process yields electrical fuses of which, in the long run
15% are defective. Find the probability that in a random sample of size n=10, fuses
selected from this process, there will be
(i) No defective fuse
(ii) At least one defective fuse
(iii) Exactly two defective fuses
(iv) At most one defective fuse
Answers
Answer:
i) 0.1969 = 19.69% probability that there will be no defective fuse.
ii) 0.8031 = 80.31% probability that there will be at least one defective fuse.
iii) 0.2759 = 27.59% probability that there will be exactly two defective fuses.
iv) 0.5443 = 54.43% probability that there will be at most one defective fuse.
Step-by-step explanation:
For each fuse, there are only two possible outcomes. Either it is defective, or it is not. The probability of a fuse being defective is independent of any other fuse, which means that the binomial probability distribution is used to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
In which \(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
And p is the probability of X happening.
15% are defective.
This means that \(p = 0.15\)
We also have:
\(n = 10\)
(i) No defective fuse
This is \(P(X = 0)\). So
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 0) = C_{10,0}.(0.15)^{0}.(0.85)^{10} = 0.1969\)
0.1969 = 19.69% probability that there will be no defective fuse.
(ii) At least one defective fuse
\(P(X \geq 1) = 1 - P(X = 0)\)
We already have P(X = 0) = 0.1969, so:
\(P(X \geq 1) = 1 - 0.1969 = 0.8031\)
0.8031 = 80.31% probability that there will be at least one defective fuse.
(iii) Exactly two defective fuses
This is P(X = 2). So
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 2) = C_{10,2}.(0.15)^{2}.(0.85)^{8} = 0.2759\)
0.2759 = 27.59% probability that there will be exactly two defective fuses.
(iv) At most one defective fuse
This is:
\(P(X \leq 1) = P(X = 0) + P(X = 1)\). So
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 0) = C_{10,0}.(0.15)^{0}.(0.85)^{10} = 0.1969\)
\(P(X = 1) = C_{10,1}.(0.15)^{1}.(0.85)^{9} = 0.3474\)
Then
\(P(X \leq 1) = P(X = 0) + P(X = 1) = 0.1969 + 0.3474 = 0.5443\)
0.5443 = 54.43% probability that there will be at most one defective fuse.
A) Find an equation for the line perpendicular to the tangent line to the curve y=x^3-4x+6 at the point (2,6)
-The equation is y=
b) What is the smallest slope on the curve? At what point on the curve does the curve have this slope?
-The smallest slope on the curve is
-The curve has the smallest slope at the point
c) Find equations for the tangent lines to the curve at the points where the slope of the curve is 8.
Answers
Answer:
f(x) = x³ - 4x + 6
f'(x) = 3x² - 4
a) f'(2) = 3(2²) - 4 = 12 - 4 = 8
6 = 8(2) + b
6 = 16 + b
b = -10
y = 8x - 10
b) 3x² - 4 = 0
3x² = 4, so x = ±2/√3 = ±(2/3)√3
= ±1.1547
f(-(2/3)√3) = 9.0792
f((2/3)√3) = 2.9208
c) 3x² - 4 = 8
3x² = 12
x² = 4, so x = ±2
f(-2) = (-2)³ - 4(-2) + 6 = -8 + 8 + 6 = 6
6 = -2(8) + b
6 = -16 + b
b = 22
y = 8x + 22
f(2) = 6
y = 8x - 10
The equation perpendicular to the tangent is y = -1/8x + 25/4
-The smallest slope on the curve is 2.92
The curve has the smallest slope at the point (1.15, 2.92)
The equations at tangent points are y = 8x + 16 and y = 8x - 16
Finding the equation perpendicular to the tangentFrom the question, we have the following parameters that can be used in our computation:
y = x³ - 4x + 6
Differentiate
So, we have
f'(x) = 3x² - 4
The point is (2, 6)
So, we have
f'(2) = 3(2)² - 4
f'(2) = 8
The slope of the perpendicular line is
Slope = -1/8
So, we have
y = -1/8(x - 2) + 6
y = -1/8x + 25/4
The smallest slope on the curveWe have
f'(x) = 3x² - 4
Set to 0
3x² - 4 = 0
Solve for x
x = √[4/3]
x = 1.15
So, we have
Smallest slope = (√[4/3])³ - 4(√[4/3]) + 6
Smallest slope = 2.92
So, the smallest slope is 2.92 at (1.15, 2.92)
The equation of the tangent lineHere, we set f'(x) to 8
3x² - 4 = 8
Solve for x
x = ±2
Calculate y at x = ±2
y = (-2)³ - 4(-2) + 6 = 6: (-2, 0)
y = (2)³ - 4(2) + 6 = 6: (2, 0)
The equations at these points are
y = 8x + 16
y = 8x - 16
Read more about tangent lines at
https://brainly.com/question/21595470
#SPJ1
Consider the following equation. 5x+3y=8 Step 1 of 2 : Determine the missing coordinate in the ordered pair (3,?) so that it will satisfy the given equation.
Answers
Answer: (3, -2.333) or (3, -7/3)
Step-by-step explanation:
We're given an x value (x=3) when looking at the coordinate, so we're trying to find what y is equal to given the equation. We can plug in x=3 into 5x+3y=8 and isolate for y.
\(5(3)+3y=8\\15 + 3y=8\\3y=-7\\y=-\frac{7}{3}\)
Answer:
y= -2 1/3
Step-by-step explanation:
Since you have x, you put x into the equation and work through the problem.
5(3)+3y=8
15+3y=8, then subtract 15 from both sides
3y=(-7), then divide both sides by 3
y=(-7)/3 or (-2 1/3)
What is the total surface area

Answers
Answer:
Step-by-step explanation:

Which of the following is a statistical question that can result in numerical data?
What is the name of your favorite pizza store?
How many hours this week did you spend on homework?
How many times did you go swimming this year?
How many pink erasers do the students in your class have?
Answers
A statistical question that can result in numerical data is How many times did you go swimming this year? So, the correct option is A).
The statistical question that can result in numerical data is "How many hours this week did you spend on homework?" and "How many times did you go swimming this year?".
These questions involve counting or measuring quantities, which can be represented using numerical data. The other two questions do not involve numerical data and therefore cannot be considered statistical questions that result in numerical data. So, the correct answer is B).
To know more about measuring quantities:
https://brainly.com/question/1504510
#SPJ1
Answer:
How many pink erasers do the students in your class have?
help please I'm not the smartest lol

Answers
Answer:
Acute angle
Step-by-step explanation:
What the meaning of statement this?


Answers
The proof demonstrates that given a well-ordered set W, an isomorphic ordinal can be found using the function F. The uniqueness of this ordinal is established using the Replacement Axioms. The set F(W) is shown to exist for each x in W, and if the least F(W) exists, it serves as an isomorphism of VV onto -y.
Lemma 2.7: This is a previously stated lemma that is referenced in the proof. Unfortunately, without the specific details of Lemma 2.7, it's difficult to provide further explanation for its role in the proof.
Well-ordered set W: A well-ordered set is a set where every non-empty subset has a least element. In this proof, W is assumed to be a well-ordered set.
Isomorphic ordinal: An ordinal is a mathematical concept that extends the notion of natural numbers to represent order and magnitude. An isomorphic ordinal refers to an ordinal that has a one-to-one correspondence or mapping with another ordinal, preserving their order and magnitude properties.
Function F: The function F is defined to assign an ordinal o to each element x in W. This means that for every x in W, there is a corresponding ordinal o.
Existence and uniqueness: The proof asserts that if there exists an ordinal o that is isomorphic to a specific initial segment of the ordinal VV (the set of all ordinals), then this ordinal o is unique. In other words, there is only one ordinal that can be mapped to the initial segment of VV given by x.
Replacement Axioms: The Replacement Axioms are principles in set theory that allow the construction of new sets based on existing ones. In this case, the Replacement Axioms are used to assert that the set F(W) exists, which is the collection of all ordinals that can be assigned to elements of W.
For each x in W: The proof states that for every x in W, there exists an ordinal o that can be assigned to it. If there is no such ordinal, the proof suggests considering the least x for which such an ordinal does not exist.
The least F(W): The proof introduces the concept of the least element in the set F(W), denoted as the least F(W). If this least element exists, it serves as an isomorphism (a one-to-one mapping) of the set of all ordinals VV onto the ordinal -y.
Overall, the proof outlines the existence and uniqueness of an isomorphic ordinal that can be obtained from a well-ordered set W using the function F, and it relies on the Replacement Axioms and the concept of least element to establish this result.
Learn more about axioms here:
https://brainly.com/question/2857184
#SPJ8
You want to put a 5 inch thick layer of topsoil for a new 26 ft by 27 ft garden. The dirt store sells by the cubic yards. How many cubic yards will you need to order? The store only sells in increments of 1/4 cubic yards.
Answers
Answer:
Step-by-step explanation:
he volume of the topsoil is
28 ft by 21 ft by 5/15 ft = 245 cubic feet
There are 27 cubic feet in one cubic yard.
245/27 = 9.074074074.... = 9.074
Need 9.25 = 9 and 1/4 cubic yards
determine whether the statement describes a population or a sample. the number of times the students on your floor order fast food in a week.
Answers
The number of times the students on your floor order pizza in a week, population.
A population is a complete set of individuals or objects that share common characteristics. It is an entire group of people, animals, plants, or objects that can be studied. A population can also be a group of people living in a certain geographical area.
A sample is a subset of a population. It is a smaller group of individuals or objects drawn from the population that are used to make inferences about the population as a whole.
A sample is used in statistical analysis to estimate population characteristics, such as mean, median, and variance. The accuracy of the estimates depends on the size and representativeness of the sample.
To learn more about a population or a sample link is here
brainly.com/question/9295991
#SPJ4
The complete question is:
Determine whether the statement describes a population or a sample. The number of times the students on your floor order pizza in a week, ___.
Question
Henry has collected data to find that the
typing speeds for the students in a typing
class has a normal distribution. What is the
probability that a randomly selected student
has a typing speed of less than 51 words per
minute if the mean (u) is 47 words per
minute and the standard deviation (o) is 4
words per minute? Use the empirical rule.
• Provide the final answer as a percent.
Provide your answer below:
%
Answers
The probability that a randomly selected student has a typing speed of less than 51 words per minute if the mean (u) is 47 words per minute and the standard deviation (o) is 4 words per minute is; 68%
How to use empirical formula in statistics?The empirical rule in statistics states that for normal distributions, 68% of observed data points will lie inside one standard deviation of the mean, 95% will fall within two standard deviations, and 99.7% will occur within three standard deviations.
The formula for z-score is;
z = (x' - μ)/σ
where;
x' is sample mean
μ is population mean
σ is standard deviation
We are given;
x' = 51
μ = 47
σ = 4
Thus;
z = (51 - 47)/4
z = 1
From empirical formula at 1 standard deviation above the means, the probability is 68%.
Read more about empirical formula at; https://brainly.com/question/10093236
#SPJ1
can someone please answer the highlighted questions? thanks!

Answers
Answer:
28 = 14 + x, 51 = 38 + x
Step-by-step explanation:
I got both sums because the last part says "is 28" and "is fifty-one," signaling that they each take up one side of the equation. Sum means add (so a + sign) and more than also means add (in this case). X just stands for the numbers not given.
Answer:
1. n+14=28 (14)
2. 38+n= 51 (13)
Step-by-step explanation:
n+14=28
-14 -14
n=14
38+n=51
-38 -38
n=13
You want to get a pizza the pizza is 14.00 but 50% off. How much will the pizza cost with 8% delivery tax Fees included?
Answers
Answer:
7.56
Step-by-step explanation:
14x.50(the remainder after you subtract the percent from 100) = 7
8% of 7 is 0.56
7+0.56=7.56
Which of the following are solutions to |x-1|=5x+2? Check all that apply.
A. x= -4/3
B. x= -1/6
C. x= 3/4
D. x= 1/6
Answers
Answer:
Step-by-step explanation: привет как вы это t6767
What is the equation of the line in slope-intercept form?
-2
=-=x+4
v=-15)+4
5
2
V=--x-4
5
2
V=--x+4
Answers
The equation of the line in slope-intercept form is y = 3x + 4.
We can use the combination formula to determine how many different packages can be created from a set of 24 crayons with 36 different colours.
The formula for the mixture is provided by:
n C r equals n!/r! (n-r)!
where r is the number of items we want to choose, n is the total number of items, and! stands for the factorial of a number, which is the sum of all positive integers up to that number.
In this instance, we are trying to determine how many various methods there are to choose 24 crayons from a set of 36 colours, regardless of the sequence in which they are chosen. Consequently, we can apply the following combination formula:
36 C 24 = 36! / (24! * 12!)
For such more questions on slope-intercept
https://brainly.com/question/1884491
#SPJ8
At the grocery store, peaches cost $2.60 per pound. Grace bought 36.8 ounces of peaches.
There are 16 ounces in 1 pound. How much did Grace spend on peaches?
Answers
Answer:
the total would be $7.00
Step-by-step explanation:
36.8 ounces = 2.3 pounds so first you add up how much it costs for 2 pounds and you get 5.20 after that you figure out how much and ounce is and that's 60 cents you add that all up and you get $7.00 (I don't know if I'm right it's been a while since I've done math like this hope it helps)
Which table shows a linear function?
-
-3
-
-2
-
MO
Answers
Find all values of m for which the equation has two real solutions.
3x² + 7x - (m + 1) = 0
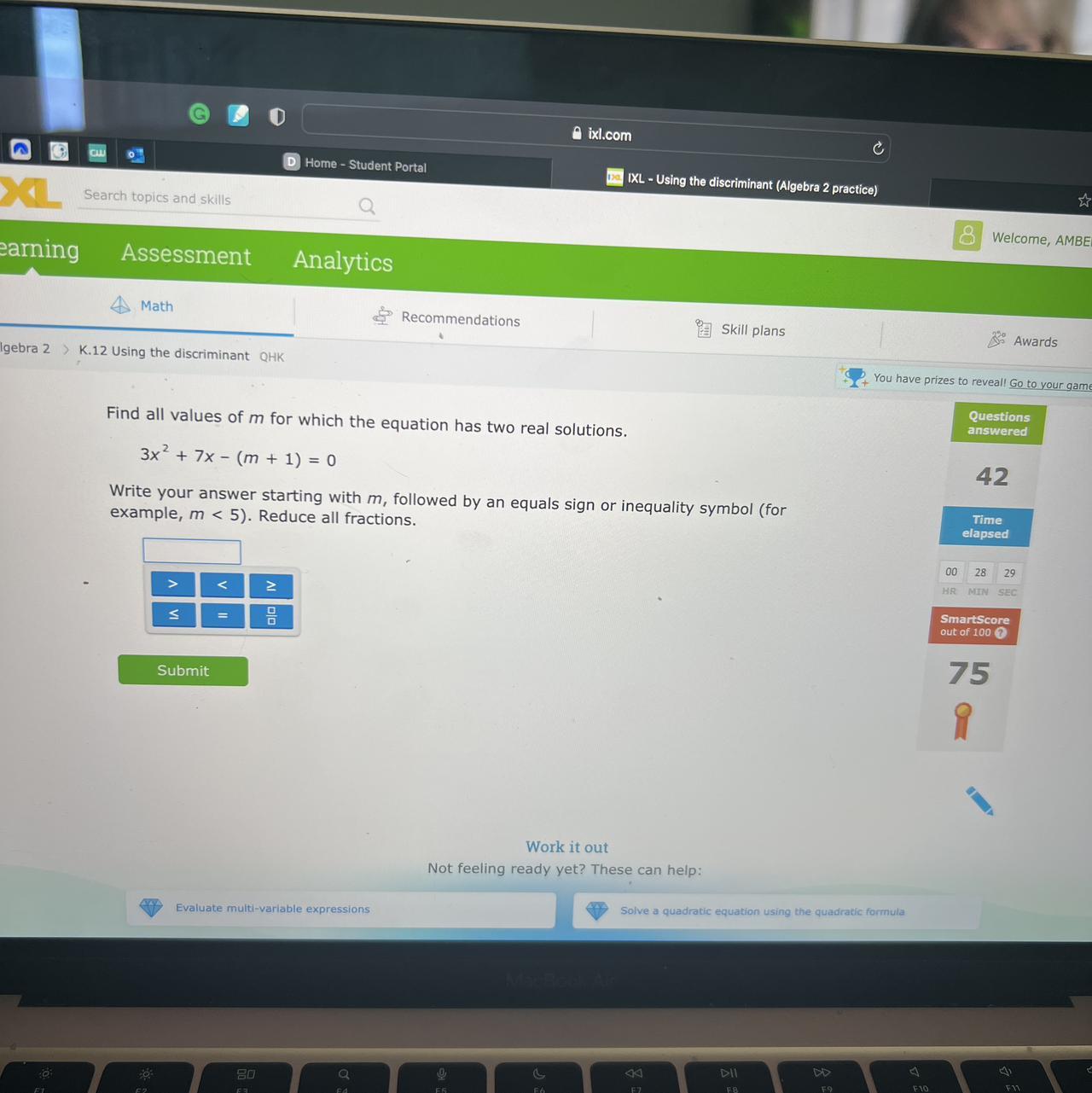
Answers

Answer:
m > - 5 1/12----------------------
Given is the quadratic equation.
A quadratic equation has two real solutions if the discriminant is positive.
Set inequality and solve for m:D = b² - 4ac, where a = 3, b = 7, c = - (m + 1)D = 7² + 4*3*(m + 1) 7² + 4*3*(m + 1) > 049 + 12m + 12 > 012m + 61 > 012m > - 61m > - 61/12 m > - 5 1/12Here are some clues about my age. • Both my father’s age and mine are 2-digit numbers. • If you reverse the order of the digits of my father’s age, you get my age. • My father is 27 years older than I am. How old am I? Show your work and justify your thinking.
Answers
For the given condition the age of the son will be 69 years.
What is the equation?A mathematical equation asserts the equality of two expressions, which may or may not contain variables or integers. Equations are fundamental concerns, and efforts to rationally address them have served as the primary driving forces behind the creation of mathematics.
Suppose the two-digit number is x,
The father's and son's ages are 10x+y and 10y+x respectively.According to the given condition,
(10x+y) -(10y+x)=27
9x-9y=27
x-y=27/9
x-y=3
The value of x and y will be 4 and 1.
At x=9 and y=6, the age of the son is obtained as,
=10×6+9
=69 years
Thus, the age of the son will be 69 years.
Learn more about the equation here,
https://brainly.com/question/10413253
#SPJ2
If the length of a rectangle is 120 m and the diagonal measures 130 m what is the perimeter and area of the rectangle
Answers
Answer:
Step-by-step explanation:
width=√(130²-120²)=√[10²(13²-12²)]=10√(13+12)(13-12)=10√(1×25)=10×5=50 m
perimeter=2(120+50)=2×170=340 m
area=120×50=6000 m²
