Answers
Answer:
B. 1/6
Step-by-step explanation:
Related Questions
Find the diameter of a circle with a
circumference of 27 centimeters. Use 3.14
for pi. Round to the nearest tenth.
Answers
Therefore, the diameter of the circle with an area of pi is 2. We can round this to the nearest tenth to get 2.0, since there are no decimal places beyond the first digit after the decimal point. Thus, the diameter of the circle is 2.0.
To find the diameter of a circle with an area of pi, we need to use the formula for the area of a circle which is A = πr^2, where A is the area of the circle, π is pi, and r is the radius of the circle.
Since we are given the area of the circle as pi, we can substitute that into the formula as follows:A = πr^2pi = πr^2Dividing both sides of the equation by pi gives us
:r^2 = 1r = sqrt(1)
Since the radius is equal to the square root of 1, which is 1, we can now use the formula for the diameter of a circle to find the diameter. The formula for the diameter of a circle is
:d = 2rd = 2(1) = 2
For such more question on decimal
https://brainly.com/question/28393353
#SPJ8
Q.3 Learn and write squares and cubes of numbers from 2 to 25 (2 times). Ex- = 2 x 2 = 4 = 2 x 2 x 2 = 8 = 3 x 3 = 9 = 3 x 3 x 3 = 27
Answers
Answer:
The squares and cubes values can be defined follows:
Step-by-step explanation:
\(Number \ \ \ \ \ \ \ \ \ \ \ \ Squares \ \ \ \ \ \ \ \ \ \ \ \ Cubes\\\\\)
\(1\ \ \ \ \ \ \ \ \ \ \ \ 1\ \ \ \ \ \ \ \ \ \ \ \ 1 \\\\2\ \ \ \ \ \ \ \ \ \ \ \ 4\ \ \ \ \ \ \ \ \ \ \ \ 8\\\\ 3\ \ \ \ \ \ \ \ \ \ \ \ 9 \ \ \ \ \ \ \ \ \ \ \ \ 27\\\\ 4 \ \ \ \ \ \ \ \ \ \ \ \ 16\ \ \ \ \ \ \ \ \ \ \ \ 64\\\\ 5\ \ \ \ \ \ \ \ \ \ \ \ 25\ \ \ \ \ \ \ \ \ \ \ \ 125\\\\ 6\ \ \ \ \ \ \ \ \ \ \ \ 36\ \ \ \ \ \ \ \ \ \ \ \ 216\\\\ 7\ \ \ \ \ \ \ \ \ \ \ \ 49\ \ \ \ \ \ \ \ \ \ \ \ 343 \\\\8\ \ \ \ \ \ \ \ \ \ \ \ 64\ \ \ \ \ \ \ \ \ \ \ \ 512\\\\\)
\(9\ \ \ \ \ \ \ \ \ \ \ \ 81 \ \ \ \ \ \ \ \ \ \ \ \ 729\\\\ 10\ \ \ \ \ \ \ \ \ \ \ \ 100 \ \ \ \ \ \ \ \ \ \ \ \ 1000\\\\11\ \ \ \ \ \ \ \ \ \ \ \ 121\ \ \ \ \ \ \ \ \ \ \ \ 1331 \\\\12\ \ \ \ \ \ \ \ \ \ \ \ 144\ \ \ \ \ \ \ \ \ \ \ \ 1728\\\\13 \ \ \ \ \ \ \ \ \ \ \ \ 169\ \ \ \ \ \ \ \ \ \ \ \ 2197 \\\\14\ \ \ \ \ \ \ \ \ \ \ \ 196 \ \ \ \ \ \ \ \ \ \ \ \ 2744\\\\ 15\ \ \ \ \ \ \ \ \ \ \ \ 225 \ \ \ \ \ \ \ \ \ \ \ \ 3375\\\\ 16 \ \ \ \ \ \ \ \ \ \ \ \ 256 \ \ \ \ \ \ \ \ \ \ \ \ 4096 \\\\\)
\(17\ \ \ \ \ \ \ \ \ \ \ \ 289\ \ \ \ \ \ \ \ \ \ \ \ 4913\\\\ 18\ \ \ \ \ \ \ \ \ \ \ \ 324\ \ \ \ \ \ \ \ \ \ \ \ 5832\\\\ 19\ \ \ \ \ \ \ \ \ \ \ \ 361\ \ \ \ \ \ \ \ \ \ \ \ 6859\\\\ 20\ \ \ \ \ \ \ \ \ \ \ \ 400 \ \ \ \ \ \ \ \ \ \ \ \ 8000 \\\\21\ \ \ \ \ \ \ \ \ \ \ \ 441\ \ \ \ \ \ \ \ \ \ \ \ 9261\\\\ 22\ \ \ \ \ \ \ \ \ \ \ \ 484 \ \ \ \ \ \ \ \ \ \ \ \ 10648\\\\ 23 \ \ \ \ \ \ \ \ \ \ \ \ 529\ \ \ \ \ \ \ \ \ \ \ \ 12167\\\\\)
\(24 \ \ \ \ \ \ \ \ \ \ \ \ 576 \ \ \ \ \ \ \ \ \ \ \ \ 13824 \\\\25\ \ \ \ \ \ \ \ \ \ \ \ 625 \ \ \ \ \ \ \ \ \ \ \ \ 15625\)
3 over 4 = 1 over 4 m

Answers
The value of m in the proportion is given as follows m = 3.
What is a proportion?A proportion is a fraction of a total amount, and the measures are related using a rule of three.
The relations between variables, either direct or inverse proportional, can be built to find the desired measures in the problem.
The proportion is defined as follows:
3/4 = (1/4)m.
As the values have a proportional relationship, the value of m can be obtained applying cross multiplication, as follows:
3/4 = (1/4)m
cross multiplication;
3/4 x 4 = m
m = 3
Hence m =3 is the value that satisfies the proportion in this problem.
More can be learned about proportions at brainly.com/question/24372153
#SPJ1
given the relation R = {P, Q, R, S, T, U, V, W, X, Y, Z} and the set of functional dependencies F = { {P, R}→{Q}, {P}→{S, T}, {R}→{U}, {U}→{V, W}, {S}→{X, Y}, {U}→{Z}}. Find the key for R? Decompose R into 2NF and then 3NF relations and then to BCNF (show the steps of decomposition steps clearly).
Answers
The resulting relations are:
R1({P, R, Q, U, Z})
R2({P, S, T}, {R → R2})
R3({U, V, W}, {R → R3})
R4({S, X, Y}, {P → R4}) or ({R → R4})
To find the key for R, we need to determine which attribute(s) uniquely identify each tuple in R. We can do this by computing the closure of each attribute set using the given functional dependencies F.
Starting with P, we have {P}+ = {P, R, U, V, W, Z}, since we can derive all other attributes using the given functional dependencies. Similarly, {R}+ = {R, U, V, W, Z}. Therefore, both {P} and {R} are candidate keys for R.
To decompose R into 2NF, we need to identify any partial dependencies in the functional dependencies F. A partial dependency exists when a non-prime attribute depends on only a part of a candidate key. In this case, we can see that {P}→{S, T} is a partial dependency since S and T depend only on P but not on the entire candidate key {P,R}.
To remove the partial dependency, we can create a new relation with schema {P, S, T} and a foreign key referencing R. This preserves the functional dependency {P}→{S,T} while eliminating the partial dependency.
The resulting relations are:
R1({P, R, Q, U, V, W, Z})
R2({P, S, T}, {R → R2})
To decompose R into 3NF, we need to identify any transitive dependencies in the functional dependencies F. A transitive dependency exists when a non-prime attribute depends on another non-prime attribute through a prime attribute.
In this case, we can see that {U}→{V,W} is a transitive dependency since V and W depend on U through the prime attribute R. To eliminate this transitive dependency, we can create a new relation with schema {U, V, W} and a foreign key referencing R.
The resulting relations are:
R1({P, R, Q, U, Z})
R2({P, S, T}, {R → R2})
R3({U, V, W}, {R → R3})
To decompose R into BCNF, we need to identify any non-trivial functional dependencies where the determinant is not a superkey. In this case, we can see that {S}→{X,Y} is such a dependency since S is not a superkey.
To remove this dependency, we can create a new relation with schema {S, X, Y} and a foreign key referencing P (or R). This preserves the functional dependency while ensuring that every determinant is a superkey.
The resulting relations are:
R1({P, R, Q, U, Z})
R2({P, S, T}, {R → R2})
R3({U, V, W}, {R → R3})
R4({S, X, Y}, {P → R4}) or ({R → R4})
Learn more about resulting from
https://brainly.com/question/1578168
#SPJ11
If the probability of a student selling brownies is 0.2, the probability of selling rootbeer floats is 0.4, and the probability of
selling brownies and rootbeer floats is 0.01, what is the probability of a student selling brownies or rootbeer floats?
Answers
Answer:
.6
Step-by-step explanation:
Answer:
Step-by-step explanation:
.59
Which situations can be modeled with a periodic function?A. Flag on windmillB. Height of baseball after being hitC. Ball suspended from strin
Answers
Answer: Situations that exhibit a repeating pattern over time or space, such as the movement of a flag on a windmill or a ball suspended from a string, can be modeled with a periodic function.
Step-by-step explanation:
A periodic function is a function that repeats itself after a certain interval. The situations that can be modeled with a periodic function are those that exhibit a repeated pattern over time or space.
A. Flag on windmill: The movement of a flag on a windmill can be modeled with a periodic function because it oscillates back and forth in a repeating pattern. The movement of the flag can be described by a sine or cosine function.
B. Height of baseball after being hit: The height of a baseball after being hit cannot be modeled with a periodic function because it does not exhibit a repeating pattern.
The height of the baseball will decrease as time passes, and it will eventually hit the ground. This behavior is not periodic.
C. Ball suspended from string: The motion of a ball suspended from a string can be modeled with a periodic function because it oscillates up and down in a repeating pattern. The motion of the ball can be described by a sine or cosine function.
Therefore, situations that exhibit a repeating pattern over time or space, such as the movement of a flag on a windmill or a ball suspended from a string, can be modeled with a periodic function.
To know more about periodic function refer here
https://brainly.com/question/29305357#
#SPJ11
a fair coin is flipped nultiple times until it lands on heads if the probability of landing on heads is 50% what is the probability of first landing on heads on the fourth attempt
Answers
If a fair coin is flipped several times until it lands on heads and the likelihood of such outcome is 50%, the probability of the coin landing on heads for the first time is 1/8.
what is probability ?There are four primary categories of probability: classical, empirical, subjective, and axiomatic. Since possibility and probability are equivalent, you may define probability as the likelihood that a specific event will occur.
given
A fair coin is repeatedly flipped until it comes up heads.
The coin is impartial.
On the third try, we need to calculate the likelihood of the first landing being on heads.
We are aware that each flip of a fair coin is independent of the others, and that each effort results in P(H) = P(T) = 0.5.
Required probability is the likelihood that the third attempt's first landing will be on heads.
= Chance of (I two trials result in tail and third result in head)
=P(I head) P(II head) P(III tail) (since each trial is independent)
= ( 1 /2 ) (1/2)(1/2) = (1/8 )
If a fair coin is flipped several times until it lands on heads and the likelihood of such outcome is 50%, the probability of the coin landing on heads for the first time is 1/8.
To know more about probability visit :-
https://brainly.com/question/30034780
#SPJ4
(Theoretical Probability MC)
Joseph has a bag filled with 3 red, 3 green, 9 yellow, and 10 purple marbles. Determine P(not green) when choosing one marble from the bag.
92%
88%
24%
12%
Answers
The probability of not selecting a green marble is equal to the total number of non-green marbles in the bag divided by the total number of marbles in the bag.
What is the meaning of probability and it will be calculated?To calculate the probability: there are three green marbles out of a total of twenty-five marbles, so the probability of selecting a green marble is 3/25.
The likelihood of not selecting a green marble is then 1 - 3/25 = 22/25.
This is equal to 22/25 * 100 = 88% as a percentage.
As a result, P(not green) = 88%
Probability denotes the possibility of something happening. It is a mathematical branch that deals with the onset of a random event. The value ranges from zero to one. Probability has been tried to introduce in mathematics to predict the probability of events occurring. Probability is defined as the degree to which something is likely to occur. This is the fundamental probability theory, which is also used in probability distribution, in which you will learn about the possible outcomes of a random experiment.
To know more about random event visit :-
https://brainly.com/question/15186748
#SPJ1
Matti is making moonshine in the woods behind his house. He’s selling the moonshine in two different sized bottles: 0.5 litres and 0.7 litres. The price he asks for a 0.5 litre bottle is 8€, for a 0.7 litre bottle 10€. The last patch of moonshine was 16.5 litres, all of which Matti sold. By doing that, he earned 246 euros. How many 0.5 litre bottles and how many 0.7 litre bottles were there? Solve the problem by using the determinant method (a.k.a. Cramer’s rule).
Answers
To determine the number of 0.5 litre bottles and 0.7 litre bottles sold by Matti, we can solve the problem using the determinant method, also known as Cramer's rule.
Let's denote the number of 0.5 litre bottles as x and the number of 0.7 litre bottles as y. We can set up a system of equations based on the given information:
0.5x + 0.7y = 16.5 (equation 1) - representing the total volume of moonshine sold
8x + 10y = 246 (equation 2) - representing the total earnings from selling the moonshine
To apply Cramer's rule, we need to calculate the determinants of the coefficient matrix and the matrices obtained by replacing each column of the coefficient matrix with the constants from equation 1 and equation 2.
The determinant of the coefficient matrix is (0.5)(10) - (0.7)(8) = -1.4.
Replacing the first column with the constants from equation 1, the determinant is (16.5)(10) - (0.7)(246) = 129.
Replacing the second column with the constants from equation 2, the determinant is (0.5)(246) - (16.5)(8) = -84.
Now, using Cramer's rule, we can solve for x and y:
x = determinant of the matrix with the first column replaced by the constants divided by the determinant of the coefficient matrix
= 129 / -1.4
= -92.14
y = determinant of the matrix with the second column replaced by the constants divided by the determinant of the coefficient matrix
= -84 / -1.4
= 60
Since we cannot have a negative number of bottles, we round x to the nearest whole number, which is 92. Therefore, Matti sold 92 bottles of 0.5 litres and 60 bottles of 0.7 litres.
Using Cramer's rule allows us to solve the problem by considering the coefficients and constants involved. By calculating determinants, we can find the values of x and y that satisfy the given equations. It is an efficient method for solving systems of linear equations, especially when there are only two variables involved.
Learn more about coefficient matrix here:
brainly.com/question/9879801
#SPJ11
A College claims that the algebra ability of their students has changed in the last few years. It was well known that students in the past could solve, on average, 10 equations per day. The College took a sample of 113 students this semester, and found that on average, the students in the sample could solve 13 equations with a sample standard deviation of 1.5. To verify the company's claim, you will perform a hypothesis test, with a significance level of 99%.
(a) State H0,H1 for this test. Is the test one-tailed or two? (b) Which type of test is to be used (Z or t)? State your reasons. (c) Compute the test statistic and nd the critical value. (d) Sketch (or plot using software) a graph showing the critical value, the region of rejection and the value of your test statistic. (e) Based on your sketch from part (d), do you support the College's claim?
Answers
The test is two-tailed because we are testing for a change in either direction. we reject the null hypothesis and support the College's claim that the algebra ability of their students has changed
(a)The hypothesis for this test can be stated as follows:
H0: The average number of equations that students can solve per day is still 10. (μ = 10)
H1: The average number of equations that students can solve per day has changed. (μ ≠ 10)
The alternative hypothesis (H1) suggests that there has been a change in the algebra ability of the students. The test is two-tailed because we are testing for a change in either direction.
(b) A t-test should be used in this case because the population standard deviation is unknown, and the sample size is relatively small (n = 113). The t-test is appropriate when the population standard deviation is unknown and when the sample size is small.
(c) To compute the test statistic, we can use the formula for the t-test:
t = (x(bar) - μ) / (s / √n)
where x(bar) is the sample mean, μ is the hypothesized population mean, s is the sample standard deviation, and n is the sample size.
Given: x(bar) = 13 μ = 10 s = 1.5 n = 113
Substituting the values into the formula, we have:
t = (13 - 10) / (1.5 / √113)
t = 2.186
(d) The critical value for a two-tailed test at a significance level of 99% can be obtained from the t-distribution table or using software. The critical value will depend on the degrees of freedom, which is n - 1 = 113 - 1 = 112.
Assuming the critical value to be tα/2,112,
(e)we can determine whether the calculated test statistic falls in the region of rejection or not. If it falls in the region of rejection, we reject the null hypothesis and support the College's claim that the algebra ability of their students has changed. If it does not fall in the region of rejection, we fail to reject the null hypothesis, indicating that there is not enough evidence to support the claim of a change in algebra ability.
To know more about two-tailed click here :
https://brainly.com/question/17038447
#SPJ4
f(x)=2x -7, What is x when f(x)=-15?
Answers
Answer:
x = -4
Step-by-step explanation:
Plug in -15 into the equation:
f(x) = 2x - 7
-15 = 2x - 7
Solve for x:
-15 = 2x - 7
-8 = 2x
-4 = x
Which system of equations has a solution at point W?
A y = -2x − 3 y = 2x − 1
B y = x + 4 y = -x + 2
C y = -2x − 3 y = x + 4
D y = 2x − 1 y = -x + 2

Answers
The system of equations has a solution at point W is:
C. y = -2x − 3
y = x + 4
What is the Solution to a System of Equations?If the coordinates of a point makes the equations of a system to be true, then it is a solution to the system of equations, and it is also the point of intersection of their lines.
Find the equation of each of the line that intersects at point W.
The declining line has a slope (m) = rise/run = -2/1 = -2
The y-intercept of the declining line is, b = -3.
Write the equation of the declining line by substituting m = -2 and b = -3 into y = mx + b:
y = -2x - 3
The increasing line has a slope (m) = rise/run = 2/2 = 1
The y-intercept of the declining line is, b = 4.
Write the equation of the declining line by substituting m = 1 and b = 4 into y = mx + b:
y = x + 4
Therefore, the system of equations is:
C. y = -2x − 3
y = x + 4.
Learn more about the system of equations on:
https://brainly.com/question/13729904
#SPJ1
4 pounds of grapes cost 5$ 7 pounds of grapes cost $8.75. What is the cost per pound?
Answers
Answer:
$1.25 per pound
the expression 2 log x - (3 log y + log z) is equivalent to
Answers
Answer:
\(2 log(x )- (3 log(y) + log(z) ) \\ \equiv log( {x}^{2} ) - log( {y}^{3} ) - log(z) \\ \equiv log( \frac{x {}^{2} }{ {y}^{3} + z} ) \)
Please help me!! Thank you!

Answers
The area of a rectangular vegetable patch is 45 square meters. The vegetable patch is 9 meters long. How wide is it?
Answers
45/ 9 = 5 meters
one side of a rectangle is 16 meters longer four times another side find the length of the sides given that the area of the rectangle is 768 square
Answers
Step-by-step explanation:
form the quadratic equation
solve for x by the use of completing square method.

an airplane flying at an elevation of 3,500 ft., directly above a straight highway. two motorists are driving cars on the highway on opposite sides of the plane. the angle of depression to one car is 31 degrees and to the other is 53 degrees. how far apart are the cars?
Answers
The first and second cars are 7724 feet apart from each other.
The angle of depression is the angle we have to move your eyes downwards to look at the car from the plane. Let's start with the first car, with the 31° angle of depression. Draw an upside-down right triangle with vertices at the plane, the car, and the point 3500 feet in the air above the car (level with the plane). The vertex at the plane is 31° and the right angle is the vertex in the air above the car. The length of the leg from the car to the point in the air above the car is 3500 feet. We like to find the length of the leg from the plane to the point in the air above the car. Since the two sides involved are the legs of the triangle, use tangent:
tan = opposite/ adjacent
⇒ tan(31°) = 3500/x
⇒ 0.60086 = 3500/x
⇒ 0.67 x = 3500 [ rounding up 0.60086 = 0.67]
⇒ x = 5223.88
That means the first car is 5223.88 feet from the point on the highway below the plane.
We can do something similar with the second car, which has an angle of depression of 53° from the plane. Again, the leg from the car to the point in the air above the car (level with the plane) is 3500 feet, the right angle is at the vertex at the point in the air above the car, and the 53° angle is at the vertex at the plane. We are looking for the length of the other leg, which runs from the plane to the point in the air above the car. Use tangent:
tan(53°) = 3500/x
⇒ 1.327 = 3500/x
⇒ 1.4x = 3500 [ rounding 1.327 = 1.4]
⇒ x = 3500/1.4
⇒ x = 2500
That means the second car is 2500 feet from the point on the highway below the plane.
Add the two distances together to get the total distance from car to car:
5223.88 + 2500.00 = 7723.88
So, rounded to the nearest foot, the cars are 7724 feet apart.
Learn more about Vertex:
https://brainly.com/question/29030495
#SPJ4
Triangle A’B’C’ is the image of triangle ABC. Which transformations could have been used to create A’B’C? Choose all that apply.

Answers
Transformations that may have been used to construct A'B'C include a 90° upward rotation and a 3 unit up and 3 unit right shift.
What is transformations?Transformation in mathematics refers to the process of changing the position, size, or shape of a geometric object. The following are the most common types of transformations: Translation: It involves moving an object from one location to another without changing its size or orientation. Reflection: It involves flipping an object over a line of reflection, so that the object and its image are mirror images of each other. Rotation: It involves rotating an object around a fixed point, called the center of rotation. Dilation: It involves changing the size of an object, either making it larger or smaller, while preserving the shape of the object. Shear: It involves skewing an object in a given direction, causing its shape to be distorted. Similarity Transformation: It is a combination of transformations that preserve the shape of an object, but changes its size and orientation.
Here,
Triangle A’B’C’ is the image of triangle ABC. Transformations could have been used to create A’B’C,
Rotation of 90° upwards.
Shift of 3 units up and 3 units to the right.
Transformations could have been used to create A’B’C is Rotation of 90° upwards and Shift of 3 units up and 3 units to the right.
To know more about transformations,
https://brainly.com/question/29641135
#SPJ1
There is a probablity of ____ that any individual at a random from
a population will fall (plus or minus) one standard deviation of
the mean.
Answers
Step-by-step explanation:
I hope this answer is helpful ):

if f (x)= x2- 2x : which of the following is the value of f (4)
Answers
A colony of bacteria starts with 9 bacteria at noon. If the number
of bacteria triples every 20 minutes, how many bacteria will be
present at 2:40 pm that afternoon?
Answers
You just input 9*3 into a calculator and hit ‘equals’ 8 times, since there are 8 20-minute increments in 2 hours and 40 min.
An algorithm is a calculation that determines how long it will take to solve a problem. True or False?
Answers
The given statement "An algorithm is a calculation that determines how long it will take to solve a problem." is False.
An algorithm is not just a calculation that determines how long it will take to solve a problem. An algorithm is a step-by-step set of instructions or a process used to solve a problem or perform a specific task. It is a systematic approach that allows a computer or human to break down a problem into smaller, manageable parts and reach a solution effectively.
Algorithms are the foundation of computer programming and can be applied in various fields such as mathematics, data processing, and problem-solving. They can be simple, like finding the largest number in a list, or complex, like solving a Rubik's Cube.
Efficiency is a key factor in evaluating algorithms. The time and resources required for an algorithm to solve a problem can vary greatly depending on the method used. However, the primary purpose of an algorithm is to provide a clear and concise procedure to reach a solution, rather than just estimating the time needed to solve a problem.
In summary, an algorithm is a well-defined process designed to perform a specific task or solve a problem, rather than just calculating the time required to do so. Its effectiveness depends on its efficiency, accuracy, and the simplicity of the steps involved.
To know more about Algorithm, refer to the link below:
https://brainly.com/question/21172316#
#SPJ11
Please answer correctly !!!!!!! Will mark brainliest !!!!!!!!!
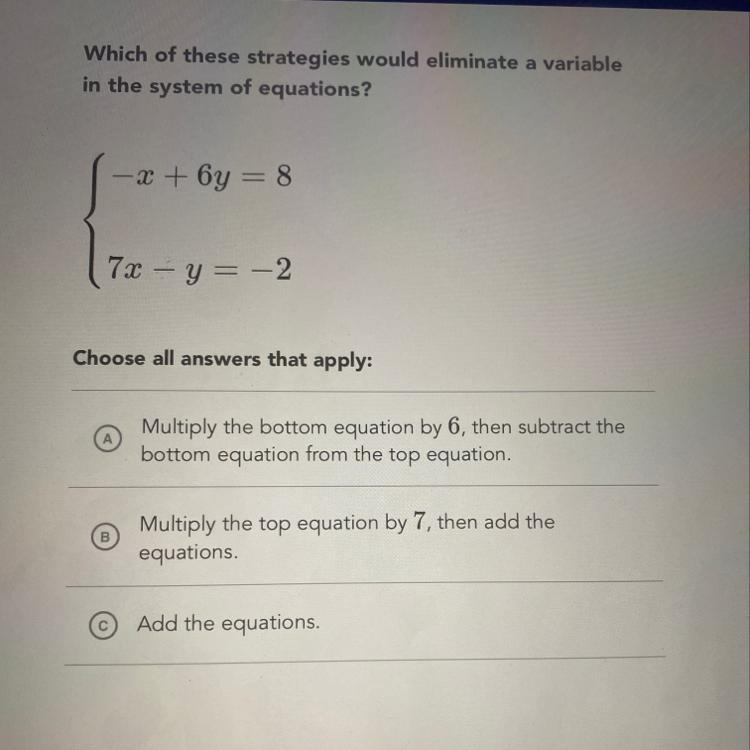
Answers
Answer:
b
Step-by-step explanation:
Use f(x) = 2x − 3 and g(x) = 4 − x2 to evaluate the expression.
(a) (f ∘ g)(x)
(b) (g ∘ f)(x)
Answers
The resulting expressions for \((f\,\circ\,g)(x)\) and \((g\,\circ\,f)(x)\) are \(5- 2\cdot x^{2}\) and \(-4\cdot x^{2} + 12\cdot x -5\), respectively.
A composition is a operation two functions in which the independent variable of the first function is substituted by the entire second function. In other words, we have the following expressions:
\((f\,\circ\,g) (x) = f(g(x))\) (1)
\((g\,\circ \,f)(x) = g(f(x))\) (2)
If we know that \(f(x) = 2\cdot x - 3\) and \(g(x) = 4 - x^{2}\), then we have the following compositions:
\((f\,\circ\, g) (x) = 2(4-x^{2})-3\)
\((f\,\circ\,g)(x) = 5-2\cdot x^{2}\)
\((g \circ f) (x) = 4 - (2\cdot x-3)^{2}\)
\((g\,\circ f) (x) = -4\cdot x^{2} +12\cdot x -5\)
The resulting expressions for \((f\,\circ\,g)(x)\) and \((g\,\circ\,f)(x)\) are \(5- 2\cdot x^{2}\) and \(-4\cdot x^{2} + 12\cdot x -5\), respectively.
We kindly invite to check this question on composition between functions: https://brainly.com/question/15070966
t=1. I need as soon as possible 1. [30 MARKS] Let t be the 7th digit of your Student ID. Answer each of the following questions:
(a) [5 MARKS] Find the limit of the following sequence:
Xn =
etn3 t2 + 3n+ (t + 1)n3
en [In(1)-In(t+2)] and qn = (Yn)2.
Define the sequences yn = =en
(b) [4 MARKS] If yn converges to I, where does a converge to? Write your answer in terms of I.
(c) [5 MARKS] Define a subsequence a, by choosing every second element of yn (i.e. ak = Y2k). Write down the first 4 elements of an. Where does this subsequence converge to if yn converges to I? Write your answer in terms of 1.
(d) [8 MARKS] Prove the following statement: A sequence can have at-most one limit.
(e) [8 MARKS] Argue whether a and q can converge to two different limits. Using your conclusion, calculate the value of the limit ..
Answers
In this question, we are provided with a sequence Xn and a related sequence Yn. We need to find the limit of Xn, determine the limit of a given subsequence yn, prove a statement regarding limits of sequences, and discuss the possibility of different limits for sequences a and q. Finally, we calculate the value of a specific limit.
(a) We are asked to find the limit of the sequence Xn. By simplifying the expression and applying limit properties, we can evaluate the limit of Xn as n approaches infinity.
(b) We need to determine where sequence a converges to if sequence yn converges to I. By understanding the relationship between the sequences and the given convergence, we can express the limit of a in terms of I.
(c) A subsequence an is defined by choosing every second element of yn. We are asked to write down the first four elements of an and identify the convergence point of this subsequence. By considering the pattern of the chosen elements, we can express the limit of an in terms of 1, based on the convergence of yn.
(d) We are required to prove the statement that a sequence can have at most one limit. By utilizing the definition of convergence and assuming two different limits, we can arrive at a contradiction, demonstrating that a sequence cannot have more than one limit.
(e) We are asked to argue whether sequences a and q can converge to different limits. By analyzing the given information and using the conclusion from part (d), we can determine whether it is possible for a and q to have distinct limits. Based on this conclusion, we then calculate the value of the specified limit.
To learn more about limit: -brainly.com/question/12211820
#SPJ11
Will give brainly and 20 points
Question 3

Answers
Answer:
I think the answer is d..
An ice machine produces ice cubes that are inch on each side.
What is the volume, in cubic inches, of one ice cube produced by this
ice machine?
Answers
The volume of an ice cube produced by this machine is of:
Volume ice cube = 1 inch³
What is a volume?A volume is the physical space that an object occupies in space, although it is also defined as the capacity of space that a hollow object may have.
If this machine produces ice that has a cube shape with a side of 1 inch, then to know the value of the volume of these cubes we will use the following equation:
Volume cube = side x side x side
Volume cube = side³
side = 1 inch
Volume ice cube = 1 inch³
As the side is 1 the volume and area will be 1 but with corresponding unit
Learn more about volume at:
https://brainly.com/question/12410983
#SPJ4
Write a polynomial with four terms that has a GCF of 4x^2.

Answers
This polynomial, 4x² is the GCF and (x + 2)(x - 1)(x + 3) are the remaining factors.
What is polynomial?
A polynomial is an equation made up of indeterminates and coefficients that only uses addition, subtraction, multiplication, and positive-integer powers of variables.
A polynomial with a GCF of 4x² means that 4x² is a factor common to all terms in the polynomial. One example of such a polynomial is:
4x² (x + 2)(x - 1)(x + 3) = 4x⁵ + 24x²- 36x³ - 72x²
In this polynomial, 4x² is the GCF and (x + 2)(x - 1)(x + 3) are the remaining factors.
To know more about polynomial visit,
https://brainly.com/question/2833285
#SPJ1
Which is a property of an angle?

Answers
Answer:
I believe that it is the last answer. have a great day!
