Answers
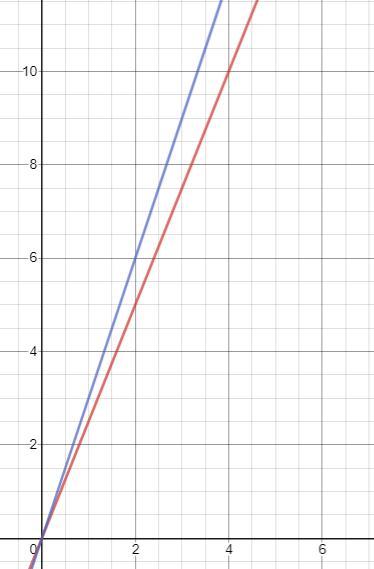
Answer: Jasmine hikes at a rate 0.5 miles per hour faster than Deandre (the third option).
Step-by-step explanation: Deandre hikes at a rate of 2.5 miles per hour, since the slope in the equation is 2.5. For Jasmin, the slope on the graph is 3 (since it goes up 3, over 1), which means she hikes at a rate of 3 miles per hour. 3 is 0.5 greater than 2.5, so Jasmin hikes at a rate that is 0.5 miles per hour faster than Deandre.
**On the graph, the blue line is Jasmin and the red line is Deandre.
Related Questions
ANSWERRRR QUICKKKK
Determine whether the graph represents a proportional relationship. (4 points)
A graph is shown. The x-axis is labeled from 0 to 9. The y-axis is labeled from 0 to 15. Four points are shown on the graph on ordered pairs 0, 2 and 1, 6 and 2, 10 and 3, 12. These points are joined by a line. The label on the x-axis is Number of cars. The title on the y-axis is Number of wheels.
a
Yes, it is a proportional relationship because the graph goes through the origin
b
Yes, it is a proportional relationship because the graph is a straight line
c
No, it is not a proportional relationship because the graph is not a straight line
d
No, it is not a proportional relationship because the graph does not go through the origin
Answers
Answer:
The correct answer is:
c. No, it is not a proportional relationship because the graph is not a straight line.
Step-by-step explanation:
A proportional relationship would be represented by a straight line passing through the origin (0, 0) on the graph. In this case, the points do not form a straight line, indicating that the relationship between the number of cars and the number of wheels is not proportional.
I need help solving this problem , I don’t understand how or what it’s asking me .

Answers
Answer:
Step-by-step explanation:
99
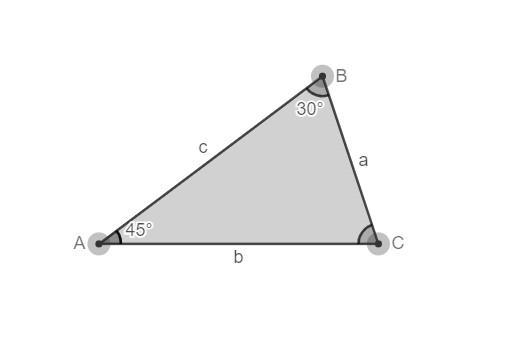
In ABC, mA = 45° and mB = 30°. To nearest
tenth, what is the ratio of the lengths of the sides
opposite to these angles?
Answers
The ratio of the lengths of the sides opposite to angles A and B is approximately 1.4.
Let's label the sides of triangle ABC as a, b, and c, with angle A opposite to side a, angle B opposite to side b, and angle C opposite to side c.
Using the Law of Sines, we have:
a/sin A = b/sin B = c/sin C
Since we know the measures of angles A and B, we can write:
a/sin 45° = b/sin 30°
Simplifying this equation, we get:
a/b = sin 45°/sin 30°
a/b = (1/√2)/(1/2)
a/b = √2
a/b ≈ 1.414
Rounding this to the nearest tenth, we get:
a/b ≈ 1.4
Therefore, the ratio of the lengths of the sides opposite to angles A and B is approximately 1.4.
Learn more about the sine rule here:
https://brainly.com/question/28061648
#SPJ1
I need help ASAP!! Please only answer if you know the answer, not if you don't.
2x - 1/4x= -28
Answers
Answer:
x = -16
Step-by-step explanation:
2x - 1/4x= -28
2x - 0.25x= -28
1.75x = -28
1.75x/1.75 = -28/1.75
x = -16
Find points on the ellipse x^2/9 y^2 closest to (2,0)
Answers
the points on the ellipse that are closest to the point (2,0) are (2, sqrt(5/9)) and (2, -sqrt(5/9)).
To find the points on the ellipse x^2/9 + y^2 = 1 that are closest to the point (2,0), we can use the method of Lagrange multipliers. We want to minimize the distance between the point (2,0) and a point (x,y) on the ellipse, subject to the constraint that the point (x,y) satisfies the equation of the ellipse. Therefore, we need to minimize the function:
f(x,y) = sqrt((x-2)^2 + y^2)
subject to the constraint:
g(x,y) = x^2/9 + y^2 - 1 = 0
The Lagrange function is:
L(x,y,λ) = sqrt((x-2)^2 + y^2) + λ(x^2/9 + y^2 - 1)
Taking the partial derivatives of L with respect to x, y, and λ, and setting them equal to zero, we get:
∂L/∂x = (x-2)/sqrt((x-2)^2 + y^2) + (2/9)λx = 0
∂L/∂y = y/sqrt((x-2)^2 + y^2) + 2λy = 0
∂L/∂λ = x^2/9 + y^2 - 1 = 0
Multiplying the first equation by x and the second equation by y, and using the third equation to eliminate x^2/9, we get:
x^2/9 + y^2 = 2xλ/9
x^2/9 + y^2 = -2yλ
Solving for λ in the second equation and substituting into the first equation, we get:
x^2/9 + y^2 = -2xy^2/2x
Multiplying both sides by 9x^2, we get:
9x^4 - 36x^2y^2 + 36x^2 = 0
Dividing by 9x^2, we get:
x^2 - 4y^2 + 4 = 0
This is the equation of an ellipse centered at (0,0), with semi-axes of length 2 and 1. Therefore, the points on the ellipse x^2/9 + y^2 = 1 that are closest to the point (2,0) are the points of intersection between the ellipse and the line x = 2.
Substituting x = 2 into the equation of the ellipse, we get:
4/9 + y^2 = 1
Solving for y, we get:
y = ±sqrt(5/9)
To learn more about ellipse visit:
brainly.com/question/19507943
#SPJ11
I don't understand these questions, could someone please help??





Answers
Answer: Question 3. 1) B=60 degrees
Step-by-step explanation: Angles on a straight line=180 so if u have 120 all you have to do is minus 180 from 120 which gives you 60.
A parabola can be drawn given a focus of (-5, -1) and a directrix of y=7. Write the equation of the parabola in any form.
Answers
A parabola with focus of (-5, -1) and a directrix of y=7 has the equation of the parabola as: (x + 5)² = 8 (y - 3)
How to write the equation of parabola with directrix of y = 7 and focus of (-5, -1)Quadratic equation = parabolic equation, when the directrix is at y direction is of the form:
(x - h)² = 4P (y - k)
OR
standard vertex form, y = a(x - h)² + k where a = 1/4p
The focus
F (h, k + p) = (-5,-1)
h = -5
k + p = -1
P in this problem, is the midpoint between the focus and the directrix
P = (-1 - 7) / 2 = -4
p = -4
the vertex
v(h, k)
h = -5
k + p = -1, k = 3
v(h, k) = v(-5, 3)
substitution of the values into the equation gives
(x - h)² = 4P (y - k)
(x - -5)² = 4 * 2 (y - 3)
(x + 5)² = 8 (y - 3)
Learn more about writing parabolic equations at:
https://brainly.com/question/28967554
#SPJ1
Find f(g(x))f(x) = 3x^2 + 2g(x) = sqrt7x^3
Answers
f(x) = 3x² + 2
g(x) = √(7x³)
Basically you need to evaluate f(x) for x = g(x), in another words, replace every x in f(x) for g(x):
f(g(x)) = 3 (√(7x³) )² + 2 = 3(7x³) + 2 = 21x³ + 2
helppp fast
Write the equation of the line in fully simplified slove-intercept form.

Answers
Answer:
y=-2/3x-6
Step-by-step explanation:
The second has initial wealth w = $2000 and expected utility preferences with a utility
inder v(r) = In(2). Suppose he faces a choice between two lotteries: p', which loses $1000 half the time and $O otherwise, and p?, which loses $500 with certainty. Calcu- late the risk premia this decision maker is willing to pay to eliminate the risk of each
of these lotteries. Which lottery does the decision-maker prefer? Explain.
Answers
The decision-maker is willing to pay a risk premium of $250 to eliminate the risk of lottery p', and a risk premium of $500 to eliminate the risk of lottery p?. Therefore, the decision-maker prefers lottery p?.
What is the rationale behind the decision-maker's preference for lottery p? over p'?The decision-maker's utility function suggests that they have a logarithmic utility index, v(r) = In(2). To calculate the risk premia, we compare the expected utilities of the lotteries. For lottery p', the expected utility is E[v(p')] = (1/2) * v(-1000) + (1/2) * v(0) = (1/2) * In(2) + (1/2) * In(2) = In(2). For lottery p?, the expected utility is E[v(p?)] = v(-500) = In(2). Since both lotteries have the same expected utility, the decision-maker is indifferent between them in terms of expected utility.
However, the decision-maker is risk-averse, which means they prefer to eliminate risk when possible. To eliminate the risk of lottery p', the decision-maker is willing to pay a risk premium of $250 (which is half the difference between the potential losses of $1000 and $0). On the other hand, to eliminate the risk of lottery p?, the decision-maker is willing to pay a risk premium of $500 (the full potential loss amount).
Therefore, the decision-maker prefers lottery p? as they are willing to pay a higher risk premium to eliminate its risk.
Learn more about Decision Making
brainly.com/question/28900762
#SPJ11
Does dividing the angle measures of a triangle change its shape?
For example, if I divide each angle measure of a triangle in half, will the triangle become smaller? Or does it not affect the size at all?
Answers
But the angles do not correlate with the length. So you can have different triangle areas/perimeters and still have the same angle size.
I hope this helps! Is a bit difficult to explain heh
The function p(x) = 5x^(4) - 3x^(3) + 2x^(2) + 24 represents how much money each girl spent based on the number of hours they were shopping. If Janelle and Carmen each go shopping for 2 hours, how much money did they spend together?
Answers
Therefore, Janelle and Carmen together spent $88 + $88 = $176.
To find out how much money Janelle and Carmen spent together, we need to evaluate the function p(x) = 5x^4 - 3x^3 + 2x^2 + 24 at x = 2 for both Janelle and Carmen.
For Janelle, when x = 2:
p(2) = 5(2)^4 - 3(2)^3 + 2(2)^2 + 24
= 5(16) - 3(8) + 2(4) + 24
= 80 - 24 + 8 + 24
= 88
For Carmen, when x = 2:
p(2) = 5(2)^4 - 3(2)^3 + 2(2)^2 + 24
= 5(16) - 3(8) + 2(4) + 24
= 80 - 24 + 8 + 24
= 88
Learn more about spent here
https://brainly.com/question/30804493
#SPJ11
You are building a rectangular brick patio surrounded by crushed stone in a rectangular courtyard. The crushed stone border has a uniform width x (in feet). You have enough money in your budget to purchase patio bricks to cover 140 square feet.
Solve the equation 140 = (20 - 2x)(16 - 2x) to find the width of the border.
Answers
Therefore, Equation 140 = (20 - 2x)(16 - 2x) simplifies to x^2 - 18x + 45 = 0, which can be solved using the quadratic formula to find x = 7.5 feet.
T solve for x, we need to first simplify the equation:
140 = (20 - 2x)(16 - 2x)
140 = 320 - 72x + 4x^2
4x^2 - 72x + 180 = 0
Dividing both sides by 4, we get:
x^2 - 18x + 45 = 0
Now we can solve for x using the quadratic formula:
x = (18 ± sqrt(18^2 - 4(1)(45))) / 2
x = (18 ± sqrt(144)) / 2
x = 9 ± 6
Since x can't be negative, we take the positive value:
x = 15/2 = 7.5 feet.
The width of the border is 7.5 feet.
To find the width of the crushed stone border (x), we need to solve the equation 140 = (20 - 2x)(16 - 2x).
Step 1: Expand the equation.
140 = (20 - 2x)(16 - 2x) = 20*16 - 20*2x - 16*2x + 4x^2
Step 2: Simplify the equation.
140 = 320 - 40x - 32x + 4x^2
Step 3: Rearrange the equation into a quadratic form.
4x^2 - 72x + 180 = 0
Step 4: Divide the equation by 4 to simplify it further.
x^2 - 18x + 45 = 0
Step 5: Factor the equation.
(x - 3)(x - 15) = 0
Step 6: Solve for x.
x = 3 or x = 15
Since the width of the border cannot be greater than half of the smallest side (16 feet), the width of the crushed stone border is x = 3 feet.
Therefore, Equation 140 = (20 - 2x)(16 - 2x) simplifies to x^2 - 18x + 45 = 0, which can be solved using the quadratic formula to find x = 7.5 feet.
To learn more about the quadratic equation visit:
brainly.com/question/28038123
#SPJ11
Ik this is not math but please help

Answers
what is the probability that the student selected will be one who both walks to school and has been late to school at least once?
Answers
15% of the time, the probability that student who chose to walk has been late.
Explain the term random variable?A random variable is either a variable with an unknown value or a function that gives values to each of the results of an experiment. Therefore, the reason why random variables are named random is because it is impossible to determine their value with certainty; instead, we can only guess, and this estimate is known as the probability that a random variable will have a given value.From the stated data-
37.5% of the 40% of students who walk to school have been late.
Thus, 37.5% of 40%
= 0.375 x 0.40
= 0.1500
= 15%
Thus, 15% of the time, the student who chose to walk has been late atleast once .
To know more about the random variable, here
https://brainly.com/question/17012084
#SPJ4
The complete question is-
At a large high school 40 percent of the students walk to school, 32 percent of the students have been late to school at least once, and 37.5 percent of the students who walk to school have been late to school at least once. One student from the school will be selected at random. What is the probability that the student selected will be one who both walks to school and has been late to school at least once?
Plez Help I’ll give brainliest

Answers
Answer: bobux man location
Step-by-step explanation: Latitude: 48.30781, Longitude: -127.14321, Distortion: 2.26
Answer:
190 millimeters
Step-by-step explanation:
you didn't show the whole question so yeah
Using the information found in these tables which of the following statements is true
Please helpppp

Answers
income consists of $320 per week plus a commission of 6% of her sales. write an algebraic expression for utako's weekly income, i , in terms of her sales, s .
Answers
The algebraic expression for Utako's weekly income in terms of her sales can be written as i = 320 + 0.06s where i is the weekly income and s is the sales.
The given algebraic expression i = 320 + 0.06s represents Utako's weekly income in terms of her sales. The expression consists of two parts - a fixed component of $320 per week and a variable component of 6% commission on her sales.
To evaluate Utako's weekly income for a particular value of sales, we simply substitute that value of s in the expression and calculate the corresponding value of i. For example, if her sales are $5000 in a week, then her weekly income would be:
i = 320 + 0.06(5000) = 320 + 300 = $620
Similarly, for any other value of sales, we can calculate her weekly income using this expression. This equation is useful for Utako to estimate her income based on her sales and to plan her finances accordingly.
To know more about algebraic expression:
https://brainly.com/question/953809
#SPJ4
plz answer my question

Answers
Answer:
65
Step-by-step explanation:
15*3+15=60
30*2+15=75
20*4+15=85
10*5+15=65
Two equations are shown. Equation 1: -0.5x-4=1.5 Equation 2: -0.5(x-4)=1.5 Select each statement that must be true. PLZ HELP ME!
Answers
Answer:
Equation 2 is correct
Step-by-step explanation:
Equation 1 is 2, not 1.5
Answer: C and D
Step-by-step explanation:
The value of c in the first one is less then the value of the second one. Also equation 1 equals -11 and equation 2 equals 1 so that’s why it’s c and d.
A linear function can be used to model the decrease in rainfall measured since 1880. The decrease in annual rainfall has been a constant 0.12 inches per year. Let x represent the number of years since 1880, when measurements began, and let y represent the annual rainfall. The initial measurement in 1880 was 54.3 inches. Use the linear function to predict the annual rainfall in the 101st year after recordkeeping began. Round to the nearest hundredth.
Answers
Answer:
42.18 inches----------------------------
In the context of the problem, - 0.12 inches per year represents the slope (negative to show a decrease) of the line and 54.3 inches represent the y-intercept as the starting point.
Considering m = - 0.12 and b = 54.3 in the slope-intercept equation:
y = mx + by = - 0.12x + 54.3Find the value of y when x = 101:
y = - 0.12(101) + 54.3 = 42.18vin Lin wants to buy a used car that costs $9,780, A10% down payment is required. (a) The used car deaier offered him a four-year add-on interest loan at 7% annual interest. Find the monthly payment. (Round your answer to the nearest cent.) 3 स (b) Find the APR of the dealer's loan, Round to the nearest hundredth of 1%. X क (c) His bank offered him a four-year simple interest amortized loan at 9.2% interest, with no fees, Find the APR, without making any calculations; x o (d) Which loan is better for him? Use the solutions to parts (b) and (c) to answer, No calculations are required. The bank's loan is better. The car dealer's ioan is better.
Answers
The bank's loan is better because it has a lower APR of 9.2% compared to the dealer's loan with an APR of 34.5%.
Given that, Vin Lin wants to buy a used car that costs $9,780. A 10% down payment is required. The used car dealer offered him a four-year add-on interest loan at 7% annual interest. We need to find the monthly payment.
(a) Calculation of monthly payment:
Loan amount = Cost of the car - down payment
= $9,780 - 10% of $9,780
= $9,780 - $978
= $8,802
Interest rate (r) = 7% per annum
Number of years (n) = 4 years
Number of months = 4 × 12 = 48
EMI = [$8,802 + ($8,802 × 7% × 4)] / 48= $206.20 (approx.)
Therefore, the monthly payment is $206.20 (approx).
(b) Calculation of APR of the dealer's loan:
As per the add-on interest loan formula,
A = P × (1 + r × n)
A = Total amount paid
P = Principal amount
r = Rate of interest
n = Time period (in years)
A = [$8,802 + ($8,802 × 7% × 4)] = $11,856.96
APR = [(A / P) − 1] × 100
APR = [(11,856.96 / 8,802) − 1] × 100= 34.5% (approx.)
Therefore, the APR of the dealer's loan is 34.5% (approx).
(c) APR of the bank's loan is less than the dealer's loan. So, the bank's loan is better for him.
(d) APR of the bank's loan is 9.2%.
APR of the dealer's loan is 34.5%.
APR of the bank's loan is less than the dealer's loan.
So, the bank's loan is better for him. Answer: The bank's loan is better.
Learn more about loan: https://brainly.com/question/20688650
#SPJ11
BRIANLY I NEED HELP PLS THE RIGHT ANSWER ASP !PLS

Answers
Answer:c
Step-by-step explanation:
math
two families with four people in each family go to a movie theater. in how many ways can they be seated
Answers
According to probability, if both families want to sit together, they can be seated in a row a maximum of two times.
What seating configuration?The direction that each person is facing is crucial when arranging the people.
In order to determine how many ways they can be seated in a row if both families want to sit together, imagine that two families with four members each attend a movie theatre.
Given that the arrangement is important, we will apply the permutation rule. We'll divide the remaining four into two groups of four each.
There are two different ways to arrange the groups so they can sit together.
2! = 2 * 1
2! = 2ways
To know more about probability visit:-
brainly.com/question/11234923
#SPJ4
you have 4 math books, 5 history books, and 2 science books. how many ways are there to arrange the books on a book shelf?
Answers
There are 5,760 ways to arrange the books on the bookshelf.
A permutation is an ordered arrangement of objects, and it can be calculated as follows:
ⁿPₓ = n! / (n - x)!
where n is the total number of objects and r is the number of objects that we are arranging.
To determine the total number of ways in which we can arrange the books on a bookshelf, we need to first calculate the total number of possible arrangements. We can do this by using the fundamental principle of counting, which tells us that the total number of possible arrangements is equal to the product of the number of ways in which each book can be arranged.
Therefore, the total number of possible arrangements can be calculated as follows:
Total number of possible arrangements = Number of ways to arrange math books × Number of ways to arrange history books × Number of ways to arrange science books
In our case, we have 4 math books, 5 history books, and 2 science books, so we can calculate the number of permutations for each type of book as follows:
Number of ways to arrange math books = ⁴P₄ = 4! / (4-4)! = 4! / 0! = 24
Number of ways to arrange history books = ⁵P₅ = 5! / (5-5)! = 5! / 0! = 120
Number of ways to arrange science books = ²P₂ = 2! / (2-2)! = 2! / 0! = 2
Now, we can substitute these values in the formula for the total number of possible arrangements:
Total number of possible arrangements = 24 × 120 × 2 = 5,760
To know more about combination here.
https://brainly.com/question/28998705
#SPJ4
i just wanna know the answers (i need to show work :/)

Answers
Answer:
Slope is -1
Step-by-step explanation:
Slope is always the number before the x in these equations.
(wish I could help you with the graphing- some of the points are: (2,1) (1,2) (3,0) (4,-1) (-1,4) )
(hope this helps!)
Stress is applied to a 20-in. steel bar that is clamped in a fixed position at each end. Let Y = the distance from the left end at which the bar snaps. Suppose Y/20 has a standard beta distribution with E(Y) = 10 and V(Y) = 100/7 a. What are the parameters of the relevant standard beta distribution? b. Compute P(8 ≤ Y ≤ 12). c. Compute the probability that the bar snaps more than 2 in. from where you expect it to.
Answers
a. The parameters of the standard beta distribution can be found using the given mean (E(Y) = 10) and variance (V(Y) = 100/7). b. By using the cumulative distribution function (CDF) of the standard beta distribution, we can calculate P(8 ≤ Y ≤ 12) as CDF(0.6) - CDF(0.4) c. probability is 0.1
The relevant standard beta distribution for the steel bar's snapping distance Y/20 has parameters that can be determined using the mean and variance provided. To compute probabilities, we can use the cumulative distribution function (CDF) and survival function (1 - CDF) of the standard beta distribution.
a. By solving the equations involving the mean and variance, we can determine the values of the parameters.
b. To compute the probability P(8 ≤ Y ≤ 12), we convert the range [8, 12] to the corresponding range in terms of Y/20, which is [0.4, 0.6].
c. To compute the probability that the bar snaps more than 2 in. from the expected position, we convert the distance of 2 in. to the corresponding value in terms of Y/20, we can calculate the probability P(Y > 2) as 1 - CDF(0.1).
learn more about beta distribution here:
https://brainly.com/question/31311746
#SPJ11
the perimeter of a rectangle is 24 inches. if the width of the rectangle is 7 inches, what is the length?
Answers
The length of the rectangle with a perimeter of 24 inches and a width of 7 inches is 5 inches.
The perimeter of a rectangle is given by the formula: P = 2l + 2w where P is the perimeter, l is the length, and w is the width. We know that the perimeter of the rectangle is 24 inches and the width is 7 inches.
Substituting the given values in the formula for the perimeter of the rectangle, we have:
24 = 2l + 2 × 7
Simplifying, 24 = 2l + 14
Subtracting 14 from both sides, we get:
10 = 2l
Dividing both sides by 2, we get: l = 5
Therefore, the length of the rectangle is 5 inches.
To know more about perimeter of a rectangle refer here:
https://brainly.com/question/29595517#
#SPJ11
4
1 point
Find the distance between the points (-5, 1) and (-1, 4) using the distance formula: (22 – 21)2 + (92 – 41)?
The distance between (-5, 1) and (-1.4) is type your answer
units.
Previous
5
7
Answers
Answer:
5Step-by-step explanation:
\(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\\\\(-5,1)\quad\implies\quad x_1=-5\,,\ \ y_1=1\\\\(-1,4)\quad\implies\quad x_2=-1\,,\ \ y_2=4\\\\d=\sqrt{(-1+5)^2+(4-1)^2}= \sqrt{4^2+3^2}=\sqrt{16+9}=\sqrt{25}=5\)
The range of a linear transformation must be a subset of the domain.a. trueb. false
Answers
False. The range of a linear transformation is a subset of the codomain, not the domain.
The domain is the set of inputs to the transformation, while the codomain is the set of possible outputs. The range is the set of actual outputs produced by the transformation. The statement "The range of a linear transformation must be a subset of the domain" is false. The range of a linear transformation is a subset of the codomain, not the domain. The domain is the set of input vectors, while the codomain contains the possible output vectors after applying the linear transformation.
To know more about linear transformation visit:
https://brainly.com/question/13595405
#SPJ11
