Solving
The product of 5 and the difference
between a number and 7 is 75. What is
the number?
Answers
The number whose product of 5 and the difference between a number and 7 is 75 is, 22.
What is a numerical expression?A numerical expression is a mathematical statement written in the form of numbers and unknown variables. We can form numerical expressions from statements.
The given statement is The product of 5 and the difference
between a number and 7 is 75.
Let, The unknown number be 'n'.
∴ 5(n - 7) = 75.
Now, 5 will move from the numerator to the denominator.
n - 7 = 75/5.
n - 7 = 15.
Now, we'll move the constant to the other side such that the variable and the constants are on different sides for our further calculation.
n = 15 + 7.
n = 22.
learn more about numerical expressions here :
https://brainly.com/question/29199574
#SPJ1
Related Questions
Solve the system by using elimination. -3x+2y=8 and -6x+7y=-8
Answers
The solution to the system is x = -8 and y = -8.
The system -3x + 2y = 8 and -6x + 7y = -8 by elimination, we need to eliminate one of the variables by adding or subtracting the two equations.
We can eliminate x by multiplying the first equation by -2 and then adding the two equations:
-2(-3x + 2y = 8) -> 6x - 4y = -16
-6x + 7y = -8
Adding these two equations eliminates the x variable:
6x - 4y = -16
-6x + 7y = -8
0x + 3y = -24
Simplifying the resulting equation gives us:
3y = -24
Dividing both sides by 3, we get:
y = -8
Now, we can substitute this value of y into either of the original equations to solve for x.
Let's use the first equation:
-3x + 2y = 8
-3x + 2(-8) = 8
-3x - 16 = 8
Adding 16 to both sides gives:
-3x = 24
Dividing both sides by -3 gives:
x = -8
For similar questions on system
https://brainly.com/question/25976025
#SPJ11
If f(x) =sqaureroot of x , which equation describes the graphed function?
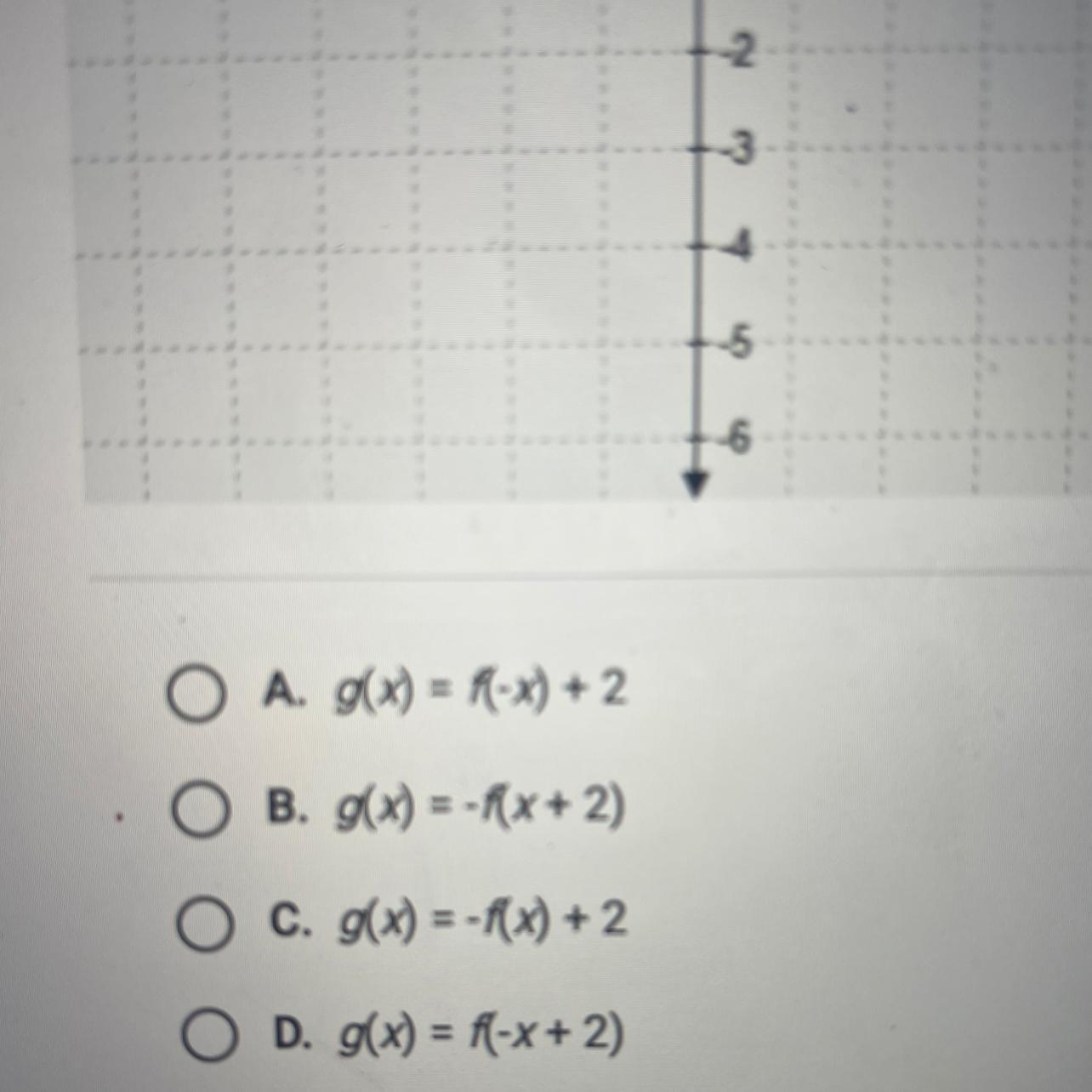
Answers
As a result, if [f(x) is (x)], then the equation [y is f(-x + 2)] defines the graphed function.
which equation describes the graphed function?[y = f(-x + 2)] is the equation that describes the graphed function.
As stated in the question, a reference graph diagram and details on the function f(x), which equals the square root of "x," are given.
From the four possibilities provided, we are expected to select the equation that best explains the graphed function.
We will employ the trial-and-error approach to this problem, employing the possibilities to identify the best solution.
First off, the graph's x-axis and y-axis are both broken at (4, 0) and respectively (0, 2). As a result, [y = f(x)] requires that our equation be equal to 0 when (x = 4) is replaced and to 2 when (x = 0).
Taking into account option (A), we obtain, by substituting (x = 4) for (y = f[(- x) + 4] = sqrt[(- x) + 4]
y = sqrt[(- 4) + 4]
furthermore, y = sqrt (4 - 4)
furthermore, y = sqrt (0)
or, y = 0
The result of replacing (x = 0) is y= [(-0)+4]
or y = sqrt(4) or y = 2 or y = (4-0)
As a result, option (A) is satisfied at locations (4, 0) and (0, 2).
Similar results may be obtained for the other three possibilities by substituting and checking: for (x = 4), (y 0), and for (x = 0), (y 2).
As a result, if [f(x) = (x)], then the equation [y = f(-x + 2)] defines the graphed function.
A function in mathematics is an operator that, given an input, will carry out a predetermined series of operations.
To learn more about graphed function refer to:
https://brainly.com/question/28700010
#SPJ1
William has a lemonade stand. Today he made $89.62 in lemonade sales and one third that amount in cookie sales. How much money did William make altogether?
Answers
Answer:
$119.49 (rounded to the nearest cent.)
Answer: 119.4933333 would be the actual answer but rounded to the nearest cent it would be 119.49
89.62/3 = 29.8733333....... 89.62 + 29.8733333 = 119.4933333
Estimate the area of a rectangle with length 5/8 foot and a width of 4/9 foot. Explain
1. 5/8 rounds to 1, and 4/9 rounds to 1. The area is about 1 sq ft.
2. 5/8 rounds to 2/3, and 4/9 rounds to 2/3. The area is about 4/9 sq ft.
3. 5/8 rounds to 1/2, and 4/9 rounds to 1/2. The area is about 1/4 sq ft.
4. 5/8 rounds to 0, and 4/9 rounds to 0. The area is about 0 sq ft.
Pick one
Answers
Solution:
Step-1: Find the area of the rectangle.
Area of rectangle = L × BL = 5/8 foot; B = 4/9 foot
=> Area of rectangle = 5/8 × 4/9=> Area of rectangle = 20/72 = 10/36 foot²Step-2: Verify all the options.
Option A => 1 ft² => 36/36 ft² Option B => 4/9 ft² => 16/36 ft² Option C => 1/4 ft² => 9/36 ft²Option D => 0 ft² => 0/36 ft²Looking at all the options, we can see that Option C (1/4 ft²) is the best estimate of the area we obtained as 10/36 and 9/36 are really close fractions.
Thus, Option C is correct.
Identify the expressions that correctly model the distance between a point located at (-2,3) and the point (x,y). Select all the apply

Answers
The distance between the two points is
d = √( -2-x)² + (3 -y)² OR d = √ (x+2)² + (y-3)².
What is distance between two points?Distance between two points is the length of the line segment that connects the two points in a plane.
The distance between two points is expressed as;
d = √ (X-x )² + (Y-y)²
X = -2
x = x
Y = 3
y = y
Therefore the distance between the two points is
d = √( -2-x)² + (3 -y)²
or it can also be written in this form
d = √ x-(-2)² + (y-3)²
d = √ x+2)² + (y-3)²
therefore the model of the distance between the two points can be
d = √( -2-x)² + (3 -y)² OR d = √ (x+2)² + (y-3)².
learn more about distance between two points from
https://brainly.com/question/7243416
#SPJ1
Three quarters of a number is 27. What is two ninths of the number?
Answers
Answer:
8
Step-by-step explanation:
let x be the number , then
\(\frac{3}{4}\) x = 27 ( multiply both sides by 4 to clear the fraction )
3x = 108 ( divide both sides by 3 )
x = 36
the number is 36, so
\(\frac{2}{9}\) × 36 = 2 × 4 = 8
The two ninths of the number is 8
We know that Three quarters of a number is \(\frac{3}{4}\) times of a number
Hence we will assume the number x ,
\(\frac{3}{4} of x = 27\)
\(x = 27 X \frac{4}{3}\)
\(x = 36\)
Now as we know the number is 36
Therefore , the two ninths of the number assumed as y
We will multiply the number 36 by 2 and then divide by 9
Hence,
\(y = 36 X \frac{2}{9}\)
\(y = 8\)
Thus, the two ninths of the number 36 is 8
Practice more quarters related questions
https://brainly.in/question/13325111
Select following series as artithmetic, geometric or neither. 1+2 +3+4+...+10
Answers
What life insurance policy never expires?
Answers
Answer:
whole life insurance
Step-by-step explanation:
Answer:
Term life insurance and Universal life
Step-by-step explanation:
If f(-2) = a and (f • g) (-2) = 2a^2, which of the following is g (-2)?
Answers
Answer: \(g(-2)=2a\)
Step-by-step explanation:
\((f \cdot g)(-2)=f(-2)g(-2)\\\\\therefore a \cdot g(-2)=2a^2 \implies g(-2)=2a\)
The function g(-2) from the given functions is 2a.
What is the function?Functions are the fundamental part of the calculus in mathematics. The functions are the special types of relations. A function in math is visualized as a rule, which gives a unique output for every input x.
The given functions are f(-2)=a and (f·g)(-2)=2a².
Here, (f·g)(-2)=2a²
f(-2)·g(-2)=2a²
a·g(-2)=2a²
g(-2)=2a²/a
g(-2)=2a
Therefore, the function g(-2) is 2a.
To learn more about the function visit:
https://brainly.com/question/28303908.
#SPJ2
When conducting a hypothesis test for a given sample size, if the probability of a Type I error decreases, then the _____________.
a. probability of incorrectly accepting the null hypothesis decreases
b. probability of Type II error decreases
c. probability of incorrectly accepting the null hypothesis increases
d. probability of incorrectly rejecting the null hypothesis increases
Answers
The probability of a Type I error is the probability of incorrectly rejecting the null hypothesis. When the probability of a Type I error decreases, the probability of a Type II error, It decreases the likelihood of choosing the null hypothesis wrongly.
When conducting a hypothesis test for a given sample size, a Type I error is the probability of incorrectly rejecting the null hypothesis. This means that the null hypothesis is true, but the hypothesis test incorrectly rejects it. A Type II error is the probability of incorrectly accepting the null hypothesis. This means that the null hypothesis is false, but the hypothesis test incorrectly accepts it. When the probability of a Type I error decreases, it means that the hypothesis test is more accurate in correctly rejecting the null hypothesis when it is false. This in turn means that the probability of a Type II error also decreases, as the test is more accurate in correctly accepting the null hypothesis when it is true. In other words, when the probability of a Type I error decreases, the probability of a Type II error decreases as well.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
A baseball team plays in a stadium that holds 60000 spectators. With the ticket price at $9 the average attendance has been 23000. When the price dropped to $7, the average attendance rose to 30000. Assume that attendance is linearly related to ticket price. What ticket price would maximize revenue?
Answers
Answer:
Step-by-step explanation:
We can start by assuming that the relationship between the ticket price and attendance is linear, so we can write the equation for the line that connects the two data points we have:
Point 1: (9, 23000)
Point 2: (7, 30000)
The slope of the line can be calculated as:
slope = (y2 - y1) / (x2 - x1)
slope = (30000 - 23000) / (7 - 9)
slope = 3500
So the equation for the line is:
y - y1 = m(x - x1)
y - 23000 = 3500(x - 9)
y = 3500x - 28700
Now we can use this equation to find the attendance for any ticket price. To maximize revenue, we need to find the ticket price that generates the highest revenue. Revenue is simply the product of attendance and ticket price:
R = P*A
R = P(3500P - 28700)
R = 3500P^2 - 28700P
To find the ticket price that maximizes revenue, we need to take the derivative of the revenue equation and set it equal to zero:
dR/dP = 7000P - 28700 = 0
7000P = 28700
P = 4.10
So the ticket price that would maximize revenue is $4.10. However, we need to make sure that this price is within a reasonable range, so we should check that the attendance at this price is between 23,000 and 30,000:
A = 3500(4.10) - 28700
A = 5730
Since 23,000 < 5,730 < 30,000, we can conclude that the ticket price that would maximize revenue is $4.10.
Celine purchased a ball of red yarn costing $2.33. She gave the cashier $7.19. How much change did the cashier give back to Celine?
Answers
Answer:
$ 4.86
Step-by-step explanation:
Subtract 7.19 and 2.33
7.19-2.33=4.86
The piecewise function represents the amount of taxes owed, f(x), as a function of the taxable income, x. Use the marginal tax rate chart or the piecewise function to answer the questions.
Tax Bracket Marginal Tax Rate
$0–$10,275 10%
$10,276–$41,175 12%
$41,176–$89,075 22%
$89,076–$170,050 24%
$170,051–$215,950 32%
$215,951–$539,900 35%
> $539,901 37%
A piecewise function f of x in seven pieces. The function is defined by part 1, which is 0 point 10 times x for x less than or equal to 10,275; part 2, which is 0 point 12 times x minus 205 point 50 for 10,276 is less than or equal to x which is less than or equal to 41,175; part 3 which is 0 point 22 times x minus 4,323 for 41,176 is less than or equal to x which is less than or equal to 89,075; part 4 which is 0 point 24 times x minus 6,105 point 50 for 89,076 is less than or equal to x which is less than or equal to 170,050; part 5 which is 0 point 32 times x minus 9,070 point 32 for 170,051 is less than or equal to x which is less than or equal to 215,950; part 6 which is 0 point 35 times x minus 26,187 point 50 for 215,951 is less than or equal to x which is less than or equal to 539,900; and part 7 which is 0 point 37 times x minus 36,985 point 67 for x is greater than or equal to 539,901.
Part A: Using the method of your choice, demonstrate how to calculate the amount of taxes owed on a taxable income of $31,000. Show all work. (4 points)
Part B: Using the taxes owed from part A, determine the effective tax rate. Show all work. (4 points)
Part C: Compare the piecewise function to the marginal tax rate chart. How is the marginal tax rate chart represented in the piecewise function? (2 points)
Answers
Answer:
Part A: $3,415.50
B: 11.34%
Step-by-step explanation:
Part A: $31,000 is within the values 10,276≤x≤41,175, so use f(x)=0.12x-205.50
Part B: For the effective tax rate, divide the amount in part A by the taxable income
Part C: Compare both the taxable income and the effective tax rate to the income domains given and the % multiplier. This one is mostly about how you describe the situation, so I'll leave that up to you.
To calculate the taxes owed on a taxable income of $31,000, we use the appropriate equation for the tax bracket it falls into and substitute the value of x. The effective tax rate is calculated by dividing the amount of taxes owed by the taxable income and multiplying by 100. The piecewise function represents the marginal tax rate chart by using different equations for each tax bracket.
Explanation:Part A:
To calculate the amount of taxes owed on a taxable income of $31,000, we need to determine which tax bracket it falls into. Since $31,000 is greater than $10,275 but less than $41,175, it falls into tax bracket 2. To find the amount of taxes owed, we use the equation for tax bracket 2: f(x) = 0.12x - 205.50. Plugging in $31,000 for x, we get:
f(x) = 0.12 * 31000 - 205.50 = $3,574.50
Therefore, the amount of taxes owed on a taxable income of $31,000 is $3,574.50.
Part B:
To determine the effective tax rate, we divide the amount of taxes owed by the taxable income. Using the result from Part A (taxes owed = $3,574.50) and the taxable income of $31,000, we have:
Effective tax rate = (taxes owed / taxable income) * 100 = (3,574.50 / 31,000) * 100 ≈ 11.52%
Therefore, the effective tax rate on a taxable income of $31,000 is approximately 11.52%.
Part C:
The piecewise function represents the amount of taxes owed as a function of the taxable income. Each part of the function corresponds to a different tax bracket, with the equation for that tax bracket. The marginal tax rate chart is represented in the piecewise function by the different equations for each tax bracket. For example, the equation in part 1 of the function (f(x) = 0.10x) corresponds to the 10% marginal tax rate for the tax bracket $0-$10,275.
Learn more about Taxes Calculations here:
https://brainly.com/question/16200743
#SPJ2
plzzz a n s w e r thiss

Answers
Answer:
oki! Mizuki is here to help!
The answer is 61 cars!
Step-by-step explanation:
First, let's find how much money she needs to earn!
105 + 500 = 605
Then, we will divide the amount she needs to earn by the amount per each car!
605 ÷ 10 = 60.5
We get 60.5 As an answer but... since we must wash a whole car, we will round it up and get 61 cars as the answer!
which of the following expression has a coefficient of 10 and a constant of 5 10+5x. 10+5. 10 - 5. 10x+5
Answers
the coefficient is the number that accompanies the variable, in this case it would be the number that accompanies the x
and a constant is a number without company
so, the expression is
\(10x+5\)the last option
urgent help algebra 2

Answers
Answer:
y = - 1/4 x + 1
Step-by-step explanation:
Find two convenient integer coordinates like -4,2 and 4, 0
use these points to calculate the slope to be -1/4
intercept is b = 1
y = -1/4 x + 1
Daija wants trim 3.5centimetes from her hair how should she move the decimal point to convert this number to millimeters

Answers
9514 1404 393
Answer:
right
Step-by-step explanation:
1.0 cm = 10. mm . . . . . . the decimal point is moved to the right
3.5 cm = 35. mm . . . . . . the decimal point is moved to the right
In one season a basketball player missed 20% of her free throws. How many free throws did she attempt if she made 200 free throws?
Answers
Answer:
She attempt 1,000 free throws
Step-by-step explanation:
X • 0.2 = 200
X = 200/0.2
X = 1,000
Which choice shows 13 • (7 • 4) correctly rewritten using the associative property and then correctly simplified?
Answers
The choice that shows 13 · (7 · 4) correctly rewritten using the associative property and then correctly simplified is presented as follows;
(13 · 7) · 4 = 91 · 4 = 364What is the associative property of multiplication?The associative property of multiplication stated that the multiplication of three numbers produces the same result in any way the numbers are grouped.
Mathematically, the associative property of multiplication can be presented as follows;
(a × b) × c = a × (b × c)
The specified operation involving the multiplication of three numbers are presented as follows;
13 · (7 · 4)
The associative property of multiplication indicates that we get;
13 · (7 · 4) = (13 · 7) · 4
13 × 7 = 91
Therefore, (13 · 7) · 4 = (13 × 7) × 4
(13 × 7) × 4 = 91 × 4 = 364
The option that shows the associative property correctly written and then correctly simplified is therefore;
(13 · 7) · 4 = 91 · 4 = 364The possible options in the question, obtained from a similar online question are;
(13 · 74) = 96213 · 4 · 7 = 52 · 7 = 364(13 · 7) · 4 = 91 · 4 = 36413 · (4 · 7) = 13 · 28 = 364
Learn more about the associative property of multiplication here:
https://brainly.com/question/17214533
#SPJ1
how do you solve simple linear equations?
Answers
9514 1404 393
Explanation:
The rules of equality tell you that you can do anything you like to an equation, as long as you do the same thing to both sides of the equal sign. This is the essence of Algebra, so is worth remembering. My teacher summarized it as "keep the equal sign sacred."
__
"Simple linear equations" come in several varieties. They are sometimes called "one-step", or "two-step", or "three step" linear equations, depending on how many steps are required to solve them. In what follows, we're using "x" as the variable, and the letters a, b, c, d as constants.
One-step
In general, the "one step" will be either an addition or a multiplication.
x + a = b . . . . an addition equation
ax = b . . . . . . a multiplication equation
The key in any case is to look at what is done to the variable and use an inverse operation to "undo" it. The opposite of addition is addition of the additive inverse (add the opposite). This is also called subtraction. For the addition equation, this looks like ...
x + a - a = b - a . . . . . . add (-a) to both sides (or subtract 'a')
x = b - a . . . . . . . . . . . the solution
The opposite of multiplication is multiplication by the multiplicative inverse (the reciprocal) This is also called division. For the multiplication equation, this looks like ...
ax(1/a) = b(1/a) . . . . . multiply by (1/a) on both sides (or divide by 'a')
x = b/a . . . . . . . . . . . the solution
__
Two-step
As with one-step linear equations, two-step equations come in some different forms.
ax +b = c
ax +b = cx
a(x +b) = c
In general, the two steps are an addition step and a multiplication step, not necessarily in that order. You will notice that the first step can transform the equation to a "one-step" equation. As before, inverse operations are involved, and whatever is done is done to both sides of the equal sign.
ax +b = c ⇒ ax = (c -b) . . . . subtract b to get a multiplication equation
In this next, we have the variable on both sides of the equal sign. we can put the variable on one side of the equal sign by adding the opposite of the term we don't want where it is. Leaving the constant alone, we can add (-ax) to both sides to get ...
ax +b = cx ⇒ b = cx -ax ⇒ b = (c -a)x
When you have numbers, you can go directly to (c-a)x by "combining terms". This is now the one-step multiplication equation.
Finally, another 2-step form is ...
a(x +b) = c ⇒ x +b = c/a . . . . . divide by 'a' to get an addition equation
This last equation can also be solved by using the distributive property first.
ax +ab = c . . . . . still a 2-step equation, now of the first type
__
Three-step
The most typical "3-step" linear equation is of the form ...
ax +b = cx +d
where both variables and constants are on both sides of the equal sign. As you may have noticed above, we prefer to have variables on one side and constants on the other side. So, add the opposite of the term you don't want where it is (to both sides, of course).
If we want variables on the left and constants on the right, we can add -cx and -b. The "3 steps" assume you do these as separate operations.
ax +b -cx = cx +d -cx ⇒ (a-c)x +b = d . . . a two-step equation
(a-c)x +b -b = d -b ⇒ (a-c)x = d-b . . . . a one-step multiplication equation
_____
Additional comments
There are some choices you can make that will tend to reduce errors. One of them involves selection of the variable term you want to eliminate (add the opposite of). Generally, if you choose the term with the lowest (most negative, left-most on the number line) coefficient, adding its opposite will result in a positive coefficient for the remaining variable term. Then when you divide by that coefficient, you're dividing by a positive number. Most folks perform arithmetic with fewer errors when they're working with positive numbers.
The general approach to any "solve for" situation is to look at what is done to the variable you're solving for. The Order of Operations is a useful lens for looking at this. When you list the operations, your "undo" sequence will start with the last operation on the list, and work backward.
Further note: your total comfort with doing arithmetic with any kind of numbers (integers, fractions, mixed-numbers, decimals, scientific notation, positive or negative) will aid you immensely. Always be careful with minus signs. They tend to get lost, forgotten, ignored, Be sure they don't.
answer first three questions for brainliest

Answers
#2 you would cross multiply again. 4 over x. = 5 over 15. 4 times 15 = 60. 5 times x = 5x. 60 divided by 5 = 12. So x=12. Sorry im not well with explanation.
Which statement about the location of √7 on the number line is true?
A= It is located at the number 7 on the number line.
B= It is located at the number 3.5 on the number line.
C= It is located between the numbers 2 and 3 on the number line.
D=It is located between the numbers 4 and 9 on the number line
Answers
Explanation
The square root of a number is “what number times itself”
2 x 2 = 4
3 x 3 = 9
7 is between 4 and 9 so C is the correct answer
You start driving east for 18 miles, turn right, and drive south for
another 5 miles. At the end of driving, what is your straight line
distance from your starting point? Round to the nearest tenth of a
mile.
Answers
Answer:
18.7
Step-by-step explanation:
Use the Pythagorean Theorem.
Simplify.
Simplify.
Square root both sides
Simplify. Ignore negative root, as length must be positive.
Round to the nearest tenth.
Answer:18.7
Step-by-step explanation:
a certain city has a population of 202,079 and covers 73.2 square miles . about how many people per square mile live in the city?
Answers
We want to know how many people per square mile live in the city. For doing so, we will do the division between the total population, and the surface of the city. This is,
\(\frac{202,079\text{ persons}}{73.2\text{ mi}}=2760.64\text{ persons/mi }\)This means that there are 2, 760.64 persons by square miles.
Write an equation in slope-intercept form for the line described. Slope 4, passes through (6,9)
Answers
Answer:
y= 4x -15
Step-by-step explanation:
Please see attached picture for full solution.

The proportion of all US adults who eat popcorn when they go to the movie theater is p = 0.87. A random sample of 20 US adults was selected and asked if they eat popcorn when they go to the movie theater. Which of the following is the shape of the sampling distribution of p hat ?
a. The sampling distribution of p hat is approximately Normal because n p = 17.4 greater-than 10.
b. Because n (1 minus p) = 20 (1 minus 0.87) = 2.6 less-than 10, the sampling distribution of p hat is not approximately Normal. The sampling distribution of p hat is skewed right and centered at 0.87.
c. Because n (1 minus p) = 20 (1 minus 0.87) = 2.6 less-than 10 , the sampling distribution of p hat is not approximately Normal. Because p = 0.87 is closer to 1 than 0, the sampling distribution of p hat is skewed to the left.
d. Because n (1 minus p) = 20 (1 minus 0.87) = 2.6 less-than 10, the sampling distribution of p hat is not approximately Normal. Because p = 0.87 is closer to 1 than 0, the sampling distribution of p hat is skewed to the right.
Answers
The option that represents shapes of the sampling distribution of p hat is:
c. Because n (1 minus p) = 20 (1 minus 0.87) = 2.6 less-than 10 , the sampling distribution of p hat is not approximately Normal. Because p = 0.87 is closer to 1 than 0, the sampling distribution of p hat is skewed to the left.
What is the shape of the sampling distribution?Normal distribution is defined as the probability curve of a continuous distribution that's most likely symmetric around the mean. On the Z curve, at Z=0, the chance is 50-50. A bell-shaped curve is another name for it.
Because the requirement for normal is greater than 10, n×p is greater than 10 and nx(1-p) is also greater than 10.
This situation is abnormal because it is not valid. If p is close to 1 in a normal graph, then p is left skewed.
Thus, the option third is correct because nx(1-p)=2.6 less than equal to 10 then the sampling distribution is not approximate normal because p=0.87 is closer to 1 than zero. Sampling distribution is skewed to the left.
Read more about Distribution shape at: https://brainly.com/question/26615964
#SPJ1
ABCD is a rhombus. Find x and yx = 80; y = 80x = 100; y = 80x = 80 ; y = 360x = 80; y = 100
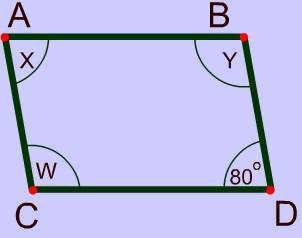
Answers
Answer: \(x=80^{\circ}, y=100^{\circ}\)
Step-by-step explanation:
\(x=80^{\circ}\) (opposite angles of a rhombus are congruent)
\(y=w=100^{\circ}\) (adjacent angles of a rhombus are supplementary)
The rate constant for first-order degradation of a N2O2 in a solution (1.0 mg/ml) at 40°C
is 0.00351 hr-1, activation energy is 2000 cal/mol, and R = 1.987 cal/mol/degree.
Calculate
a. The rate constant for first-order degradation of N2O2 at room temperature (25°C).
Answers
The 0.0035 hr⁻¹ first-order degradation rate constant in the 40 °C, 1.0 mg/ml solution, where R = 1.987 cal/mol/degree and 2,000 cal/mol activation energy indicates;
a. The rate constant for first-order degradation of N₂O₂ at room temperature is approximately 4.12595 × 10⁻² hr⁻¹
What is a first-order reaction?A first order reaction is one that has a rate that varies linearly with the concentration of one reactant
The given parameters are;
Temperature of the solution = 40°C
T₁ = 40 °C + 273.15 = 313.15 K
The rate constant, K₁ = 0.00351 hr⁻¹
Concentration of the solution = 1.0 mg/ml
Activation energy, Eₐ = 2000 Cal/mol
R = 1.987 cal/mol/degree
The formula by which the rate constant can be found is presented as follows;
\(log\dfrac{k_2}{k_1} =\dfrac{E_a}{2.303\times R} \times \dfrac{T_2-T_1}{T_1\cdot T_2}\)
a. Room temperature = 25 °C
T₂ = 25 °C + 273.15 = 298.15 K
Therefore;
\(log\dfrac{k_2}{0.00351} =\dfrac{2000}{2.303\times 1.987} \times \dfrac{313.15-298.15}{313.15 \times 298.15}\)
\(k_2=0.00351 \times 10^{\left(\dfrac{2000}{2.303\times 1.987} \times \dfrac{313.15-298.15}{313.15 \times 298.15}\right)} \approx 4.12595\times 10^{-2}\)
The rate constant for first-order degradation of N₂O₂ at room temperature is k₂ ≈ 4.12595 × 10⁻² hr⁻¹Learn more about the rate constant for first-order degradation here:
https://brainly.com/question/14595397
#SPJ1
Mariana and her best friend are attending a concert in a large auditorium. They just climbed up 125 steps. The number of steps they climbed can be represented by
zero
positive
negative
Answers
The number of steps they climbed can be represented by positive
How to represent the number of steps?From the question, we understand that they climbed up
Upward movements are usually represented by the positive sign
This means that:
Steps = 125 or +125
Hence, the number of steps they climbed can be represented by positive
Read more about positive numbers at
https://brainly.com/question/1782403
#SPJ1
¿puede un número ser múltiplo de más de un número? RESPONDAN RAPIDO
Answers
Yes, a number can be a multiple of more than one number.
What are numbers?Numbers are representations of quantity or quality.
We have many types of numbers such as,
- Real numbers
- Rational numbers
- Irrational numbers
- Complex numbers
- Even numbers
- Odd numbers
- Whole numbers
We have,
A number can be a multiple of more than one number.
For example:
12 is a multiple of both 2 and 3, as it can be divided evenly by both of these numbers.
Similarly,
30 is a multiple of both 5 and 6, as it can be divided evenly by both of these numbers.
Thus,
Yes, a number can be a multiple of more than one number.
Learn more about numbers here:
https://brainly.com/question/17429689
#SPJ9
The complete question.
Can a number be a multiple of more than one number?