Answers
Answer:
4
Step-by-step explanation:
Related Questions
Evaluate x(y+3)/(3+y)z for x=12, y=1, and z=6.
A) 2
B) 5
C) 8
D) 6

Answers
Answer:
2
Step-by-step explanation:
We take the equation
\(x(y+3)/(3+y)z\)
and substitute the values for each individual variable in the problem. It looks like this:
\(12(1+3)/(3+1)6\)
Now we can solve the equation.
When solved, it equals 2.
Calculate the area of the shaded segments in the following diagrams. (a) 12 cm 40° (b) 58° 16 cm
Answers
(a) 12 cm 40° : Area of shaded segments = 301.44 sq. cm.
(b) 58° 16 cm : Area of shaded segments = 777.04 sq. cm.
Explain about the sector of circle?Two radii that meet at the center to form a sector define a circle. The sector is the portion of the circle created by these two radii. Knowing a circle's central angle calculation and radius measurement are both crucial for solving circle-related difficulties.
Area of sector of circle = Ф/360 * πr²
π = 3.14
r is the radius
Ф is the angle subtended.
(a) 12 cm 40°
Area of shaded segments = 40/60 * 3.14* 12²
Area of shaded segments = 40/60 * 452.16
Area of shaded segments = 301.44 sq. cm.
(b) 58° 16 cm
Area of shaded segments = 58/60 * 3.14* 16²
Area of shaded segments = 58/60 * 803.84
Area of shaded segments = 777.04 sq. cm.
Know more about the sector of circle
https://brainly.com/question/22972014
#SPJ1
The diagram for the question is attached.

the approximate mass of Mars is 6.42x10^23 kilograms. write this mass in standard notation
Answers
Answer:
642000000000000000000000 kg
Step-by-step explanation:
The approximate mass of Mars is 6.42x10^23 kilograms. It is given in scientic notation.
We need to write the mass in standard notation. It is the normal way of writing any number. To write it in standard form, we move the decimal to the right side.
The standard form will be :
6.42x10^23 kg = 642000000000000000000000 kg
Hence, this is the required solution.
The commutative property does not work for which operations?check all that applys.
Answers
Answer: The commutative property states that the numbers on which we operate can be moved or swapped from their position without making any difference to the answer. The property holds for Addition and Multiplication, but not for subtraction and division.
Step-by-step explanation:
Hope this is right!!!!
two sides of a triangle measure 5 in and 12 in what could be the length of the third side
Answers
Answer:
b
Step-by-step explanation:
Half the sum of x and 7

Answers
Can someone help me I have to verify the trig identities.

Answers
The trigonometric identities are verified that they are true.
What are trigonometric expressions?
Trigonometric identities are, by definition, reciprocal. These formulas show the connections between the sine/cosine functions and tangents.
1. LHS = sec x [ sec x - cos x]+(sin x+ cos x)/sin x- cot x
= sec²x - sec x cos x +(sin x+ cos x)/sin x - cos x/sin x
= sec²x - cos x/cos x +(sin x+ cos x- cos x)/sin x
= sec²x - 1 + sin x /sin x
= sec²x - 1 +1
= sec²x
= RHS
2. LHS = cos (π-Θ)+ sin (π/2 + Θ)
= - cos Θ + cos Θ
= 0
= RHS
To learn more about trigonometric identities here,
https://brainly.com/question/7331447
#SPJ1
PLEASE FAST
What is the equation of the line containing the paints A and B?
a) y = - 3x + 4
b) y = 1/3x + 4
c) y = 3x + 4
d) y = - 1/3x + 4

Answers
The equation of the line containing the paints A and B is y = -1/3x + 4
How to determine the linear equation that represents the graphfrom the question, we have the following parameters that can be used in our computation:
The graph
Where, we have
(6, 2) and (0, 4)
A linear equation is represented as
y = mx + c
Where
c = y when x = 0
So, we have
y = mx + 4
Using the other points, we have
6m + 4 = 2
So, we have
6m = -2
Evaluate
m = -1/3
So, we have
y = -1/3x + 4
As an equation, we have
y = -1/3x + 4
Read more about linear relation at
https://brainly.com/question/30318449
#SPJ1
Rewrite the equation in simplified slope-intercept form: 77-y=5x
Answers
The equation of the line in slope - intercept form is -
y = - 5x + 77.
What is the equation of a straight line in slope - intercept form?The equation of a straight line in slope - intercept form is -
y = mx + c
{m} - slope.
{c} - intercept along the y - axis.
Given is the equation as -
77 - y = 5x
We have the equation in the slope - intercept form as -
77 - y = 5x
y = 77 - 5x
y = - 5x + 77
Therefore, the equation of the line in slope - intercept form is -
y = - 5x + 77.
To solve more questions on straight lines, visit the link below -
brainly.com/question/28951560
#SPJ1
Find the missing value
Put answer in simplest form
Please Show Your Work

Answers
when running a line, in a right-triangle, from the 90° angle perpendicular to its opposite side, we will end up with three similar triangles, one Small, one Medium and a containing Large one. Check the picture below.
\(\cfrac{x}{7}=\cfrac{28}{x}\implies x^2=196\implies x=\sqrt{196}\implies x=14\)

tHanks again everyone

Answers
Let's solve
\(\\ \rm\rightarrowtail x+2<-3\)
\(\\ \rm\rightarrowtail x<-3-2\)
\(\\ \rm\rightarrowtail x<-5\)
So
there is a open dot present over -5Less than means left side onwardsOption B
O LINEAR EQUATIONS AND INEQUALITIES
Graphing a compound inequality o...
Graph the compound inequality on the number line.
x>-8 and x≤-3

Answers
The compound inequality on the number line is shown below.
We have been given a compound inequality. We are asked to graph the given inequality on number line.
x>8 and x≤3
The solution for the inequality is all values of x less than or equal to 3 and greater than or equal to 8.
We will have solid dots at x>-8 and x≤-3 .
One arrow of the number line would be from 3 to left of the number line (towards negative infinity). The other arrow will be from 8 to right side of number line towards positive infinity.
Learn more about number line at:
https://brainly.com/question/24644930
#SPJ1

Which statement is true about this quadratic equation?
y = 12 – 1lr + 7
OA.
There is one real solution.
B.
There are two real solutions.
OC.
There are two complex solutions.
D.
There is one complex solution.
Answers
Answer:
C
Step-by-step explanation:
Which statement is true.
Answers
A party planner is going to use an arch of balloons for a parade of recent graduates. The estimated curve the
balloons will create is modeled by the function given in the table, where x represents the distance in feet along
the ground from the start and f(x) represents the height in feet above the ground.
The planner needs a clearance of 9 feet under the arch. Has the planner met the minimum height?
No, because the width of the arch is 8 feet
Yes, because the width of the arch is 9.6 feet
No, because the maximum height of the arch is 8 feet
Yes, because the maximum height of the arch is 9.6
feet

Answers
Answer:
Option (4)
Step-by-step explanation:
Party planner has used an arc of balloons for the parade.
This arc starts from x = 0 along the ground and f(x) defines the height of the arch.
From the table attached, it is clear that at x = 4 maximum height of the arch is 9.6 feet.
Therefore, clearance space below the arc is 9.6 feet which is greater than 9 feet, minimum height required for the clearance of the parade.
Option (4) will be the answer.
Answer:
D. yes, because the maximum height of the arch is 9.6 feet
Step-by-step explanation:
EDGE 2020 :)
Please help will give brainlest!!

Answers
That’s it
Y= -x + 2
Because it goes back one unit on the X axis and goes up two units.
Peter and Joey and Tommy made $42.18 for the lemonade stand if they split the profit evenly how much will each of the boys get
Answers
Step by step guide:
Start by dividing 18 by 2 and you get 9 or think of a number that can be multiplied by 2 to get 18, so far each boy has 0.09 cents
Next 42 divided by 2 which is $21
Finally add $21 and 0.09€ and you get $21.09
Standard form of 0=2-y
Answers
Answer:
y = 2
Step-by-step explanation:
0 = 2 - y
-2 = -y
y = 2
Answer:
it'll always be the number it is if it's going by 0
What is the equation of the line that is parallel to the line defined by the equation y = 3x−7 and goes through the point (4, 2)?
Answers
Answer:
\(y-2=3(x-4)\)
Step-by-step explanation:
Pre-SolvingWe are given a line contains the point (4, 2).
We also know that the line is parallel to y= 3x - 7.
We want to write the equation of this line.
Parallel lines have the same slopes.
First, let's find the slope of y = 3x - 7.
3 is in the place of where m (the slope) is, so that means it is the slope of that line.
It is also the slope of the line whose equation we want to write.
The equation of the line can be written in three ways:
Slope-intercept form, which is y=mx+b, where m is the slope and b is the y-intercept. Standard form, which is ax+by=c, where a, b, and c are free integer coefficients. a and b cannot be 0, and a is usually non-negative as well. Point-slope form, which is \(y-y_1=m(x-x_1)\), where m is the slope and \((x_1, y_1)\) is a point.All of these ways are valid, but for this problem, let's write the equation in point-slope form, as it is the easiest.
SolvingSubstitute 3 as m in \(y-y_1=m(x-x_1)\).
\(y-y_1=3(x-x_1)\)
Now, substitute 4 as \(x_1\) and 2 as \(y_1\).
\(y-2=3(x-4)\)
Topic: parallel and perpendicular lines
See more: https://brainly.com/question/7699889
please..............

Answers

Answer:
C = 50P
750 dollars
Step-by-step explanation:
$50 per person and P represents each person, and C is the total cost basically, so:
C = 50P, is the equation
To find 15 people, just plug it in
C = 50P
C = 50(15)
C = 750
Explain how special right triangles, reference angles, and quadrants of a coordinate grid help us find the exact answer to the following: cos 210°.
Answers
9514 1404 393
Answer:
cos(210°) = -(√3)/2
Step-by-step explanation:
The terminal ray of a 210° angle is in the third quadrant. The angle it makes with the -x axis is (210° -110°) = 30°. This is the "reference angle". In the 3rd quadrant, the x-coordinate of the terminal ray's intersection with the unit circle has a negative sign. This will be the sign of the cosine of the angle.
__
The reference angle of 30° tells you that the trig functions of the angle can be found from the side ratios of the "special right triangle" with angles of 30°, 60°, and 90°. The side ratios, shortest to longest, in that triangle are 1 : √3 : 2.
The cosine of the angle is the ratio ...
Cos = Adjacent/Hypotenuse
In the above special triangle, the side adjacent to the 30° angle is the one that is √3 ratio unis. The hypotenuse is 2 ratio units. So, the cosine of 30° is ...
cos(30°) = (√3)/2
As we said above, the sign of the adjacent side of the reference angle for 210° has a negative value. (The hypotenuse is always considered to be positive.) Then the desired cosine is ...
cos(210°) = -cos(30°)
cos(210°) = -(√3)/2

MY NOTES Two stoves are located 45 feet apart, one giving out]] 4 times as much heat as the other. If you stand at a point on the line between the stoves at a distance x from the less powerful stove, the temperature of the air is given by H(x)=100 + 60 x2 + 240 (45−x)2 . Assume you move back an forth between the two stoves, always at least 4 ft from either stove.
Answers
Missing Part of the question:
a) Assume you wish to determine the maximum and minimum temperatures you would experience. the domain to study for the function H(x) would be?
b)The is one critical number for the function on the domain in part a and it is?
c) The maximum temperature you would experience is ?
d) The minimum temperature you would experience is ?
Answer:
a. Domain : \(4 \leq x \leq 41\)
b. Critical point: \(x = 12.33\)
c. The maximum is 115.09
d. The minimum is 100.62
Step-by-step explanation:
Given
\(H(x) = 100 + \frac{60}{x^2} + \frac{240}{(45 - x)^2}\)
Solving (a): The domain of H(x)
From the question, we understand that the distance between the two stores is 45ft
Let the first stove be at point A (0 ft) and
the second stove be at point B (45ft)
Since you move back and forth within 4ft from either stoves, then
Your maximum distance at A is (0 + 4) ft = 4ft
Your minimum distance at B is (45 - 4) ft = 41ft
Hence, the domain is: \(4 \leq x \leq 41\)
Solving (b): Critical Value
First, we have to differentiate H(x) w.r.t x
\(H(x) = 100 + \frac{60}{x^2} + \frac{240}{(45 - x)^2}\)
Differentiate
\(H'(x) = 0 -\frac{120}{x^3} + \frac{480}{(45- x)^3}\)
\(H'(x) = -\frac{120}{x^3} + \frac{480}{(45- x)^3}\)
Equate H'(x) to 0
\(0 = -\frac{120}{x^3} + \frac{480}{(45- x)^3}\)
Rewrite as:
\(\frac{120}{x^3} = \frac{480}{(45- x)^3}\)
Cross Multiply
\(480 * x^3 = 120 * (45 -x)^3\)
\(480 * x^3 = 120 * (45 -x)*(45 -x) * (45 -x)\)
\(480 * x^3 = 120 * (2025 -90x +x^2) * (45 -x)\)
\(480 * x^3 = 120 * (91125 -4050x +45x^2 -2025x - 90x^2 - x^3)\)
\(480 * x^3 = 120 * (91125 -4050x -2025x+45x^2 - 90x^2 - x^3)\)
\(480 * x^3 = 120 * (91125 -6075x-45x^2 - x^3)\)
Divide both sides by 120
\(4x^3 =91125 -6075x-45x^2 - x^3\)
\(4x^3 +x^3-91125 +6075x+45x^2= 0\)
\(5x^3-91125 +6075x+45x^2= 0\)
\(5x^3+45x^2 +6075x-91125= 0\)
Divide through by 5
\(x^3+9x^2 +1215x-18225= 0\)
Solving for x, we have that
\(x\approx \:12.33067\)
\(x = 12.33\)
Hence, the critical point is 12.33
Solving (x): Maximum temperature
Here, we simply substitute the endpoints of the domain in \(H(x) = 100 + \frac{60}{x^2} + \frac{240}{(45 - x)^2}\)
Let x = 4
\(H(4) = 100 + \frac{60}{4^2} + \frac{240}{(45 - 4)^2}\)
\(H(4) = 100 + \frac{60}{16} + \frac{240}{(41)^2}\)
\(H(4) = 100 + \frac{60}{16} + \frac{240}{1681}\)
\(H(4) = 100 + 3.75+ 0.14277215942\)
\(H(4) = 103.892772159\)
\(H(4) = 103.89\) --- approximated
Let x = 41
\(H(41) = 100 + \frac{60}{41^2} + \frac{240}{(45 - 41)^2}\)
\(H(41) = 100 + \frac{60}{41^2} + \frac{240}{4^2}\)
\(H(41) = 100 + \frac{60}{1681} + \frac{240}{16}\)
\(H(41) = 100 + 0.03569303985 + 15\)
\(H(41) = 115.03569304\)
\(H(41) = 115.04\) ---- approximated
Compare both values: The maximum is 115.09
Solving (d): The minimum temperature
In (b), we have that:
\(x = 12.33\) --- critical point
The minimum occurs at this point
Substitute 12.33 for x in \(H(x) = 100 + \frac{60}{x^2} + \frac{240}{(45 - x)^2}\)
\(H(12.33) = 100 + \frac{60}{12.33^2} + \frac{240}{(45 - 12.33)^2}\)
\(H(12.33) = 100 + \frac{60}{12.33^2} + \frac{240}{32.67^2}\)
\(H(12.33) = 100 + \frac{60}{152.0289} + \frac{240}{1067.3289}\)
\(H(12.33) = 100 + 0.39466180443 + 0.22486039682\)
\(H(12.33) = 100.619522201\)
\(H(12.33) = 100.62\) --- approximated
Hence, the minimum is 100.62
giving 90 points! NEED IN TWO MINS

Answers
Answer:
300
Step-by-step explanation:
A=wl=10·30=300
multiply the length of the rectangle by the width of the rectangle.
The area is measurement of the surface of a shape. To find the area of a rectangle or a square you need to multiply the length and the width of a rectangle or a square. Area, A, is x times y.
Answer:
Area = 378.5 ft²
Step-by-step explanation:
The figure is having two semi circles and one rectangle.
\({ \sf{area = area \: of \: semicircles + area \: of \: rectangle}} \\ \\ { \sf{area = 2( \frac{1}{2} \pi {r}^{2}) + (l \times w) }} \\ \\ { \sf{area = \pi {r}^{2} + (l \times w) }} \\ \\ { \sf{area = 3.14 \times {5}^{2} + (30 \times 10)}} \\ \\ { \sf{area = 378.5 \: {ft}^{2} }}\)
f(x) = -2x^2+3x-6
how does the function open
Answers
Compare -8 and 3. Which statement is not true?
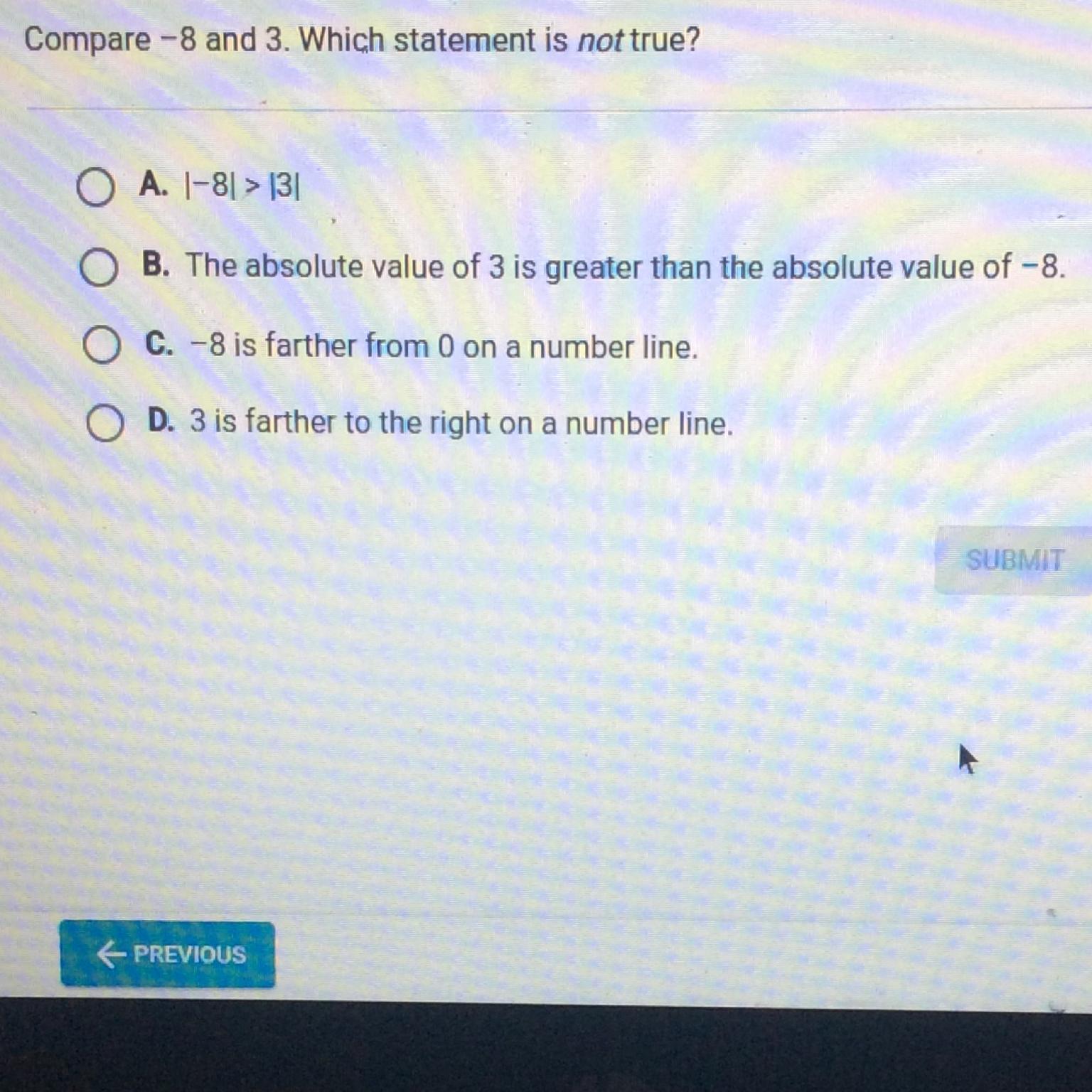
Answers
Answer:
B
Step-by-step explanation:
it is the opposite of A, which is true, as |-8| = 8
Use the diagram to find the value of the following. what is the value of x.
Angle A-
Angle B -
Angle C-

Answers
Answer:
x=29 angle a=63 Ang b=46 and c=71
Step-by-step explanation:
2x+5+x+17+3x-16=180 (sum of angles in triangles)
value of x is 29 substitute it in angle a b c
a=2*29+5
=63
b=29+17 = 46
c=3*29-16 = 71
What should substitution should've ended used to rewrite x^8-3x^4+2=0 as a quadratic equation
Answers
Step-by-step explanation:
is the answer something like x^12=-2
Does (2,-3) satisfies the equation 5x+3y=1
Answers
Answer: Yes
Step-by-step explanation: We're going to have to substitute
in the coordinates of that ordered pair into the equation.
I am going to substitute in the x and substitute in the y.
So it's really 5(2) + 3(-3) = 1.
From here it should be pretty straightforward,
all we are doing is evaluating the statement.
Simplifying on the left we have 10 + -9 = 1 or 1 = 1.
Now we know that the ordered pair (2, -3) satisfies this equation.
I NEED HELP 30 POINT!!

Answers
Answer:
35
Step-by-step explanation:
You can easily graph this in desmos for a visual understanding.
The slope of a line is received by (y2-y1)/(x2-x1). Assuming that Days is X and the cost is Y, we get (160-90)/(4-2), and it makes 70/2, which equates out to 35. Because the prices become more and more expensive, the slope is positive 35.
help pls i’m so confused !!
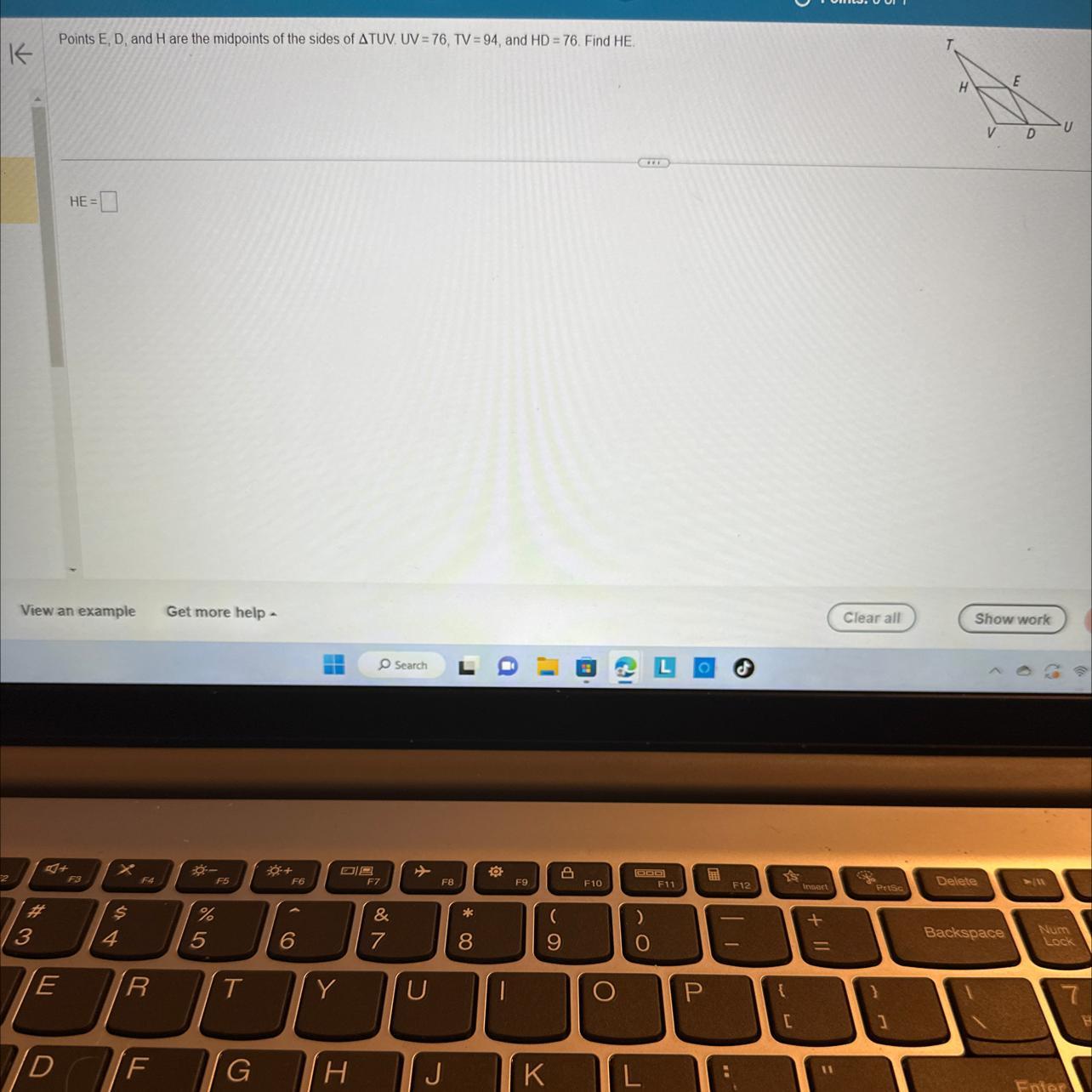
Answers
Answer: it’s 25
Step-by-step explanation:
15 +10