solve the given arithmetic operations using binary numbers.
(1101101)2 x (1001)2
Answers
Answer:
1111010101
Step-by-step explanation:
(1101101)2 x (1001)2 I used binary calculator.
Related Questions
Dose the line of reflection have to be a linear equation or can it be a exponential or a quadratic equation
Answers
Answer:
it can be all three
Step-by-step explanation:
What are some values to make -2x> 10 true ?
Please help ASAP!
Answers
Answer:
-6 -7 -8 -9 -10
Step-by-step explanation:
anything that keeps going from there dont do anything like -5 -4 -3 -2 -1 because it would be wrong
any negative number that keeps increasing after -6
3 to 2 if there are 120 children who like pizza, how many total
Answers
Answer:
320
Step-by-step explanation:
Is the 3 to 2 part to part? Out of every 5 people, 3 prefer pizza and 2 do not. We can us this to set up a proportion.
3/5 = 120/x The 3 represent the part that like pizza over the whole of 5. The second ratio is showing the actual number of people that liked pizza over the total number of people.
What would be multiply 3 by to get 120? 40. So, we will multiply 5 times 40 to get the total number of people. 5 x 40 = 200
Pls answer this quickly. I need at atleast 70%

Answers
The equation of the line with yellow point in slope intercept form is y = 7 / 6 x + 2.
How to find the equation of a line?The equation of a straight line can be represented in different form such as slope intercept form, point slope form, etc.
Therefore, let's represent the line with yellow point in slope intercept form.
Hence,
y = mx + b
where
m = slopeb = y-interceptTherefore, using (0, 2) and (6, 9).
m = 9 - 2 / 6 - 0
m = 7 / 6
Hence, let's find the y-intercept
y = 7 / 6 x + b
2 = 7 / 6(0) + b
b = 2
Therefore,
y = 7 / 6 x + 2.
learn more on slope intercept form here:https://brainly.com/question/29146348
#SPJ1
11. x and Y are complementary angles and Tan x = 3√3. Find the value of
\( \frac{1}{2 - tan \: y\\ } \)
Hence rationalise the surd
Answers
Answer:
\(\frac{1}{2-tan(y)} = \frac{3\sqrt{3}}{6\sqrt{3}-1}\)
After Rationalising:
\(\frac{1}{2-tan(y)} = \frac{54 +3\sqrt{3}}{107}\)
Step-by-step explanation:
tan(x) = 3√3
x + y = 90 (complimentary angles)
⇒ x = 90 - y
tan(\(\frac{\pi}{2}\) - θ) = cot(θ)
⇒ tan(90 - θ) = cot(θ)
⇒ tan(90 - y) = cot(y)
⇒ tan(x) = cot(y)
⇒ cot(y) = 3√3
⇒ \(\frac{1}{tan(y)}\) = 3√3
⇒ tan(y) = \(\frac{1}{3\sqrt{3}}\)
\(2-tan(y) = 2 - \frac{1}{3\sqrt{3}} \\\\= \frac{2*3\sqrt{3} -1}{3\sqrt{3} } \\\\= \frac{6\sqrt{3} -1}{3\sqrt{3} }\\\\\\\implies \frac{1}{2-tan(y)} \\\\= \frac{3\sqrt{3}}{6\sqrt{3}-1}\)
Multiply and divide by : 6(√3) + 1
\(\frac{3\sqrt{3}}{6\sqrt{3}-1}\frac{6\sqrt{3}+1}{6\sqrt{3}+1}\\ \\= \frac{(3*6*\sqrt{3}*\sqrt{3}) + 3\sqrt{3}}{6^2 * (\sqrt{3})^2 -1^2}\\\\= \frac{18*3 +3\sqrt{3}}{36*3 -1}\\\\= \frac{54 +3\sqrt{3}}{108-1}\\\\= \frac{54 +3\sqrt{3}}{107}\)
A store is having a sale on jelly beans and almonds. For 3 pounds of jelly beans and 5 pounds of almonds, the total cost is $27. For 9 pounds of jelly beans and
7 pounds of almonds, the total cost is $51. Find the cost for each pound of jelly beans and each pound of almonds.
Cost for each pound of jelly beans:
Cost for each pound of almonds:
Answers
Answer:
Cost for each pound of jelly beans: $2.75
Cost for each pound of almonds: $3.75
Step-by-step explanation:
Let J be the cost of one pound of jelly beans.
Let A be the cost of one pound of almonds.
Using the given information, we can create a system of equations.
Given 3 pounds of jelly beans and 5 pounds of almonds cost $27:
\(\implies 3J + 5A = 27\)
Given 9 pounds of jelly beans and 7 pounds of almonds cost $51:
\(\implies 9J + 7A = 51\)
Therefore, the system of equations is:
\(\begin{cases}3J+5A=27\\9J+7A=51\end{cases}\)
To solve the system of equations, multiply the first equation by 3 to create a third equation:
\(3J \cdot 3+5A \cdot 3=27 \cdot 3\)
\(9J+15A=81\)
Subtract the second equation from the third equation to eliminate the J term.
\(\begin{array}{crcrcl}&9J & + & 15A & = & 81\\\vphantom{\dfrac12}- & (9J & + & 7A & = & 51)\\\cline{2-6}\vphantom{\dfrac12} &&&8A&=&30\end{array}\)
Solve the equation for A by dividing both sides by 8:
\(\dfrac{8A}{8}=\dfrac{30}{8}\)
\(A=3.75\)
Therefore, the cost of one pound of almonds is $3.75.
Now that we know the cost of one pound of almonds, we can substitute this value into one of the original equations to solve for J.
Using the first equation:
\(3J+5(3.75)=27\)
\(3J+18.75=27\)
\(3J+18.75-18/75=27-18.75\)
\(3J=8.25\)
\(\dfrac{3J}{3}=\dfrac{8.25}{3}\)
\(J=2.75\)
Therefore, the cost of one pound of jelly beans is $2.75.
Use the Divergence Theorem to calculate the surface integral S F · dS; that is, calculate the flux of F across S. F(x, y, z) = x2yi + xy2j + 3xyzk, S is the surface of the tetrahedron bounded by the planes x = 0, y = 0, z = 0, and x + 2y + z = 2.
Answers
Answer:
-14 / 3
Step-by-step explanation:
- Divergence theorem, expresses an explicit way to determine the flux of a force field ( F ) through a surface ( S ) with the help of "del" operator ( D ) which is the sum of spatial partial derivatives of the force field ( F ).
- The given force field as such:
\(F = (x^2y) i + (xy^2) j + (3xyz) k\)
Where,
i, j, k are unit vectors along the x, y and z coordinate axes, respectively.
- The surface ( S ) is described as a tetrahedron bounded by the planes:
\(x = 0 \\y = 0\\x + 2y + z = 2\)
\(z = 0\\\)
- The divergence theorem gives us the following formulation:
\(_S\int\int {F} \,. dS = _V\int\int\int {D [F]} \,. dV\)
- We will first apply the del operator on the force field as follows:
\(D [ F ] = 2xy + 2xy + 3xy = 7xy\)
- Now, we will define the boundaries of the solid surface ( Tetrahedron ).
- The surface ( S ) is bounded in the z - direction by plane z = 0 and the plane [ z = 2 - x - 2y ]. The limits of integration for " dz " are as follows:
dz: [ z = 0 - > 2 - x - 2y ]
- Now we will project the surface ( S ) onto the ( x-y ) plane. The projection is a triangle bounded by the axes x = y = 0 and the line: x = 2 - 2y. We will set up our limits in the x- direction bounded by x = 0 and x = 2 - 2y. The limits of integration for " dx " are as follows:
dx: [ x = 0 - > 2 - 2y ]
- The limits of "dy" are constants defined by the axis y = 0 and y = -2 / -2 = 1. Hence,
dy: [ y = 0 - > 1 ]
- Next we will evaluate the triple integral as follows:
\(\int\int\int ({D [ F ] }) \, dz.dx.dy = \int\int\int (7xy) \, dz.dx.dy\\\\\int\int (7xyz) \, | \limits_0^2^-^x^-^2^ydx.dy\\\\\int\int (7xy[ 2 - x - 2y ] ) dx.dy = \int\int (14xy -7x^2y -14 xy^2 ) dx.dy\\\\\int (7x^2y -\frac{7}{3} x^3y -7 x^2y^2 )| \limits_0^2^-^2^y.dy \\\\\int (7(2-2y)^2y -\frac{7}{3} (2-2y)^3y -7 (2-2y)^2y^2 ).dy \\\\\)
\(7 (-\frac{(2-2y)^3}{6} + (2-2y)^2 ) -\frac{7}{3} ( -\frac{(2-2y)^4}{8} + (2-2y)^3) -7 ( -\frac{(2-2y)^3}{6}y^2 + 2y.(2-2y)^2 )| \limits^1_0\\\\ 0 - [ 7 (-\frac{8}{6} + 4 ) -\frac{7}{3} ( -\frac{16}{8} + 8 ) -7 ( 0 ) ] \\\\- [ \frac{56}{3} - 14 ] \\\\\int\int {F} \, dS = -\frac{14}{3}\)
At the sleepover, Drew's friends ate 3 3/9 cups of ice cream. The next day, his family ate 2 4/9 cups more. How many cups did they eat altogether?
Answers
Right triangles ABC and DBC

Answers
Answer:
The writing is blurry. Please snap again in closer range
PLEASE HELP ME!!!!! I NEED HELP ASAP!!! Thank you

Answers
Answer
the answer is 90 (C)
Step-by-step explanation:
Beth = x
Caroline = 60 + x (because if Beth has 60 less than Caroline then Caroline has 60 more than Beth)
Since the ratio = 1/3 ( another way of writing 1:3) then x/60+x = 1/3
3x = 60 + x
3x - x = 60
2x = 60
x = 60/2
x = 30 (Beth has 30 stickers)
Caroline has 60 + x stickers = 60 + 30 = 90
Write an equation for the function graphed below

Answers
The rational function graphed in this problem is defined as follows:
y = -2(x - 1)/(x² - x - 2).
How to define the rational function?The vertical asymptotes of the rational function for this problem are given as follows:
x = -1 and x = 2.
Hence the denominator of the function is given as follows:
(x + 1)(x - 2) = x² - x - 2.
The intercept of the function is given as follows:
x = 1.
Hence the numerator of the function is given as follows:
a(x - 1)
In which a is the leading coefficient.
Hence:
y = a(x - 1)/(x² - x - 2).
When x = 0, y = -1, hence the leading coefficient a is obtained as follows:
-1 = a/2
a = -2.
Thus the function is given as follows:
y = -2(x - 1)/(x² - x - 2).
More can be learned about rational functions at brainly.com/question/1851758
#SPJ1
helppppppppppppppppppppppppppppppppppppppppp

Answers
Answer:
character
Step-by-step explanation:
I think Character because character is basically position and who you're playing as
Natalie borrowed money from her parents to pay for a trip.
Natalie will pay her parents in equal amounts every week until she pays back the entire amount she borrowed.
The table below shows the amount of money Natalie still owes her parents at the end of every two weeks for the first eight weeks.
Number of Weeks Natalie Has Paid,
�
w
Amount Natalie Still Owes,
�
d
0
0
$
180
$180
2
2
$
162
$162
4
4
$
144
$144
6
6
$
126
$126
8
8
$
108
$108
Part A
How much does Natalie pay her parents each week?
$
per week
Part B
Write a function that shows the relationship between the amount Natalie still owes,
�
d, and the number of weeks she has paid,
�
w.
Answers
Natalie will pay her parents $9 each week, and the initial amount she still owed was $180.
We can see that Natalie is reducing the amount she owes by $18 every two weeks.
Therefore, the amount she owes after 2 weeks is $180 - $18 = $162, after 4 weeks is $144, after 6 weeks is $126, and after 8 weeks is $108.
This means that after n weeks, the amount she still owes is:
$180 - $18n
Since she will pay the same amount each week, let's call the weekly payment P. After one week, she will owe:
$180 - P
After two weeks, she will owe:
($180 - P) - P = $180 - 2P
After four weeks, she will owe:
($180 - 2P) - P - P = $180 - 4P
After six weeks, she will owe:
($180 - 4P) - P - P = $180 - 6P
And after eight weeks, she will owe:
($180 - 6P) - P - P = $180 - 8P
We can set up an equation using the information we have:
$180 - 8P = $108
Solving for P, we get:
P = $9
Therefore, Natalie will pay her parents $9 each week, and the initial amount she still owed was $180.
To learn more about the linear equation;
https://brainly.com/question/29739212
#SPJ1
The complete question:
Natalie borrowed money from her parents to pay for a trip. Natalie will pay her parents in equal amounts every week until she pays back the entire amount she borrowed. The table below shows the amount of money Natalie still owes her parents at the end of every two weeks for the first eight weeks. How much does Natalie pay her parents each week? What is the initial amount Natalie still owes?
Week 0 = $180
Week 2 = $162
Weeks 4 = $144
Week 6 = $126
Week 8 = $108
PLEASE YALL HELP ME WITH THIS I NEED IT FOR RN
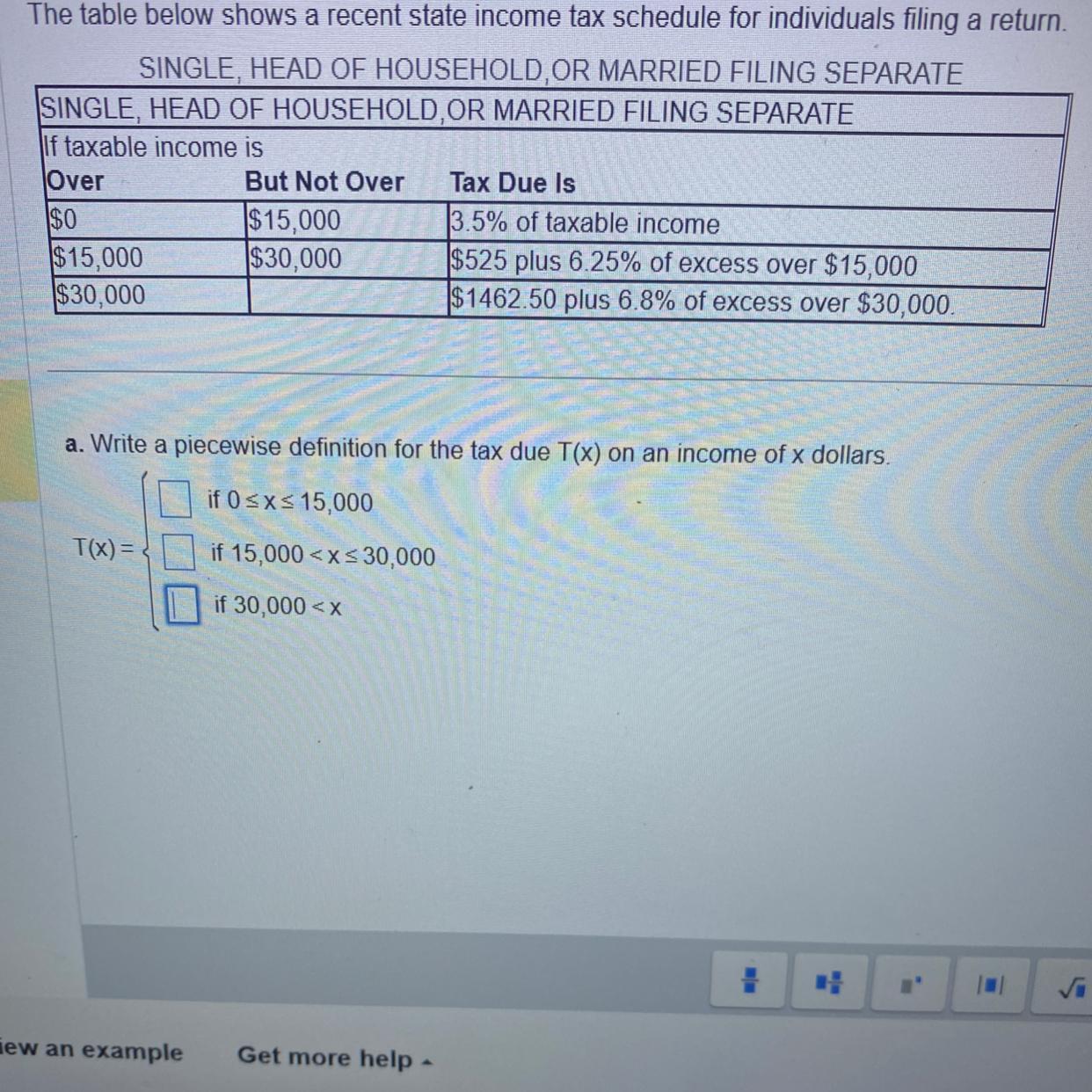
Answers
The piecewise function for the Tax due on an income of x dollars are:
T(x) = 0.035x; if 0 < x ≤ $15,000T(x) = 525 + 0.0625 (x- 15,000); if 15,000 < x ≤ 30,000 T(x) = 1462.50 + 0.068 (x - 30,000); if 30,000 < xFrom the case, we know that there are 3 scenariois for filling tax due based on an individual's income, where:
Between $0 until $15,000 is taxed 3.5% of taxable incomeBetween $15,000 until $30,000 is taxed $525 plus 6.25% of excess over $15,000Over $30,000 is taxed $1462.50 plus 6.8% of excess over $30,000.To construct the piecewise function for the Tax due, we need to translate the given conditions into mathematical formulation.
We assume that:
T(x) = tax due
x = $ amount of taxable income
For taxable income between $0 until $15,000, the tax is 3.5% of taxable income; then:
T(x) = 3.5% x
T(x) = 0.035x
For taxable income between $15,000 until $30,000, the tax is $525 plus 6.25% of excess over $15,000. Then:
T(x) = 525 + 6.25% (x - 15,000)
T(x) = 525 + 0.0625 (x- 15,000)
Please note that the additional 6.25% only will be counted based on the remaining of the taxable income deducted by $15,000.
For taxable income over than $30,000, the tax is $1462.50 plus 6.8% of excess over $30,000. Then:
T(x) = 1462.50 + 6.8% (x - 30,000)
T(x) = 1462.50 + 0.068 (x - 30,000)
Please note that the additional 6.8% only will be counted based on the remaining of the taxable income deducted by $30,000.
Learn more about Piecewise Function here: brainly.com/question/17883583
#SPJ1
Need help on this!!! Pls help!!!

Answers
a) The mean of the data-set is of 2.
b) The range of the data-set is of 4 units, which is of around 4.3 MADs.
How to obtain the mean of a data-set?The mean of a data-set is obtained as the sum of all observations in the data-set divided by the number of observations in the data-set, which is also called the cardinality of the data-set.
The dot plot shows how often each observation appears in the data-set, hence the mean of the data-set is obtained as follows:
Mean = (1 x 0 + 5 x 1 + 3 x 2 + 5 x 3 + 1 x 4)/(1 + 5 + 3 + 5 + 1)
Mean = 2.
The range is the difference between the largest observation and the smallest, hence:
4 - 0 = 4.
4/0.93 = 4.3 MADs.
More can be learned about the mean of a data-set at brainly.com/question/1156334
#SPJ1
Use the Pythagorean Theorem to solve for the missing side. Round to the nearest whole
number. Show your solution."
(4 Points)
24
6
Answers
If there is an image I cannot see it, so I solved it two different ways:
If 24 is the hypotenuse and 6 is one of the other sides:
6^2+x^2=24^2
36+x^2=576
x^2=540
x~23
If 24 is not the hypotenuse and is a side along with 6:
24^2+6^2=x^2
576+36=x^2
sqrt(612)=x
x~25
Answer:
√540 ≈ 23.2 or 23
Step-by-step explanation:
You only gave two numbers 24 and 6 and you asked for the missing side length using the Pythagorean Theorem. So because you have the number 24 which is the biggest number compared to 6 so we know that the equation for (PT) is a^2 + b^2 = c^2 so set it up like this a^2 + 6^2 = 24^2. You subtract do to wanting a side length and not the hypotenuse. When you get a number you are not finished you have to find the square root which is that number squared and you can use a number line or a calculator to help you figure out what it is equal to approximately.
a^2 + 6^2 = 24^2
a^2 - 36 = 576
-36 -36
= 540
a^2 = 540
a = √540
√540 ≈ 23.2 or 23
Write the equation of the parabola that has the same shape as f(x)=-3 x² but with vertex (5,9) in the form f(x)=a(x-h)²+k.
f(x)=?

Answers
The equation of the parabola as described in the task content is; f (x) = -3 (x - 5)² + 9.
What is the equation of the parabola as described in the task content?It follows from the task content that the equation of the parabola which has the same shape as f(x)=-3 x² but with vertex (5,9) in the form f (x) = a (x-h)² + k be determined.
Recall that the vertex of a quadratic equations of the given form is defined by the coordinates (h, k).
On this note, the required equation of the parabola by substitution of h and k is;
f (x) = -3 (x - 5)² + 9.
Read more on vertex form equation;
https://brainly.com/question/28034101
#SPJ1
help me asap. my exam is tomorrow.

Answers
The total surface area of the doghouse is 1452 ft²
What is surface area?The area occupied by a three-dimensional object by its outer surface is called the surface area.
The dog house has many surfaces including the roofs . The total surface area is the sum of all the area of the surfaces.
area of the roof part = 2( 13×11) + 2( 12× 10)×1/2
= 286 + 720
= 1006 ft²
surface area of the building
= 2( lb + lh + bh) -bh
= 2( 10× 11 + 10×8 + 11×8) - 10×11
= 2( 110+80+88)-110
= 2( 278) -110
= 556 -110
= 446ft²
The total surface area = 1006 + 446
= 1452 ft²
learn more about surface area from
https://brainly.com/question/16519513
#SPJ1
Match each expression with A, B, C or D.
A=a^3
B=6a
C=12a
D=3a^2
i)3a x 4
ii)a^2xa
iii) 6 1/2 a^2

Answers
The matching expressions are:
\(i) 3a x 4 = C (12a)\\ii) a^2 x a = A (a^3)\\iii) 6 × 1/2 a^2 = D (3a^2)\)
i) 3a x 4 can be represented as C (12a) since multiplying 3a by 4 gives 12a.
ii) a^2 x a can be represented as A (a^3) since multiplying a^2 by a gives a^3.
iii) \(6 \times 1/2 a^2\) can be represented as D (3a^2) since multiplying 6 by 1/2 and then by a^2 gives 3a^2.
To understand the matching expressions, let's break down each one:
i) 3a x 4:
This expression represents multiplying a variable, 'a', by a constant, 4. The result is 12a, which matches with C (12a).
ii) a^2 x a:
This expression represents multiplying the square of a variable, 'a', by 'a' itself. This results in a^3, which matches with A (a^3).
iii) 6 × 1/2 a^2:
This expression involves multiplying a constant, 6, by a fraction, 1/2, and then multiplying it by the square of 'a', a^2. The final result is 3a^2, which matches with D (3a^2).
Therefore, the matching expressions are:
i) 3a x 4 = C (12a)
ii) a^2 x a = A (a^3)
iii) 6 × 1/2 a^2 = D (3a^2)
for such more question on matching expressions
https://brainly.com/question/12270624
#SPJ8
A store manager is marking down easels from $40 to $28. What is the discount, as a
percentage?
Write your answer using a percent sign (%).
Answers
Answer:
30% discount
that's a big discount!
Answer:
30%
Step-by-step explanation:
Please help I will give brainily and more, NEEDING SMART PEOPLE
On the coordinate plane shown below, points
G and I
have coordinates (6 ,4) and (3 ,2), respectively.
1.) Design a strategy in which the Pythagorean theorem is used to calculate the straight line distance between points
G and I on a coordinate plane. Use complete sentences to describe the strategy.
2.) Use the Pythagorean theorem to determine the distance between the two points on the coordinate plane. In your final answer, include all of your calculations.
3.) Use the distance formula and the coordinates of points G and I
to prove that the Pythagorean theorem is an alternative method for calculating the distance between points on a coordinate plane. In your final answer, include all of your calculations.
Answers
Answer:Given : points G and I have coordinates (6,4) and (3,2)
To Find : Use Pythagorean theorem to calculate the straight line distance between points G and I
Solution:
points G and I have coordinates (6,4) and (3,2)
Draw a line parallel to y axis passing through G
Draw a line parallel to x axis passing through I
Intersection point K ( 6 , 2)
IK = 6 - 3 = 3
GK = 4 -2 = 2
ΔIKG right angled triangle
Pythagoras' theorem: square on the hypotenuse of a right-angled triangle is equal to the sum of the squares of the other two perpendicular sides.
GI² = IK² + GK²
=> GI² = 3² + 2²
=> GI² = 13
=> GI = √13
using distance formula
G (6,4) and I (3,2)
= √(6 - 3)² + (4 - 2)²
= √3² + 2²
= √9 + 4
= √13
Learn More:
different approaches of Pythagoras theorem - Brainly.in
brainly.in/question/10516214
13. In Fig. 16.10, BCDE is a rectangle , ED = 3.88 cm,AD= 10 cm ...
brainly.in/question/19749562
Rewrite the equation B - 11,015 = 2t as a function of t.
A.
B(t) = 2t + 11,015
B.
B(t) = -2t + 11,015
C.
B(t) = 2t - 11,015
D.
This equation cannot be written as a function of t.
Answers
Answer:
A
Step-by-step explanation:
B - 11,015 = 2t ( add 11,015 to both sides )
B = 2t + 11,015 , that is
B(t) = 2t + 11,015
Answer:
A. B(t) = 2t + 11015
Step-by-step explanation:
Original equation:
B - 11015 = 2t
Add 11015 to both sides:
⇒ B = 2t + 11015
Write as function of t:
⇒ B(t) = 2t + 11015
ANSWER PLEASE
A football player runs 5/6 of a mile every 3/4 of an hour how much does he run in one hour?
Answers
Answer:
5/8
Step-by-step explanation:
Answer:
Step-by-step explanation:4/0
Enter an inequality that represents the description, and then solve.
Dave has $10 to spend on a $7 book and two birthday cards (c) for his friends. How much can he spend
on each card if he buys the same card for each friend.
Answers
Answer:
$1.50 per card
Step-by-step explanation:
Knowns:
$10 to spends, Wants to buy $7 book and two equal priced cards.
10 = 7 + 2x
Subtract 7 from both sides to find out how much money Dave has after he buys his book.
3 = 2x
Divide each side by 2 to find out how much he cana spend on each card
x = 1.50
i hope this helps!
-TheBusinessMan
10. In the diagram, RP bisects SRQ. P S R If m SRP =5x - 10 and m-QRP =3x + 20, what is the measure in degrees of m_SRQ?

Answers
Answer:
55
Step-by-step explanation:
If RP bisects SRQ. P S R, then the measure of m<SRQ is 130degrees
A line that bisects an angle divides the angles into two equal parts
If RP bisects SRQ from the diagram shown, then;
m<SRP = m<PRQm<SRP + <PRQ = m<SRQGiven the following:
m SRP =5x - 10 and m-QRP =3x + 20
5x - 10 = 3x + 20
5x - 3x = 20 + 10
2x = 30
x = 30/2
x = 15
Get the measure of SRQ
m<SRQ = 5x - 10 + 3x + 20
m<SRQ = 8x + 10
m<SRQ = 8(15) + 10
m<SRQ = 120 + 10
m<SRQ = = 130degrees
Hence the measure of m<SRQ is 130degrees
Learn more here; https://brainly.com/question/17247176
Ernest plans to attend Community College for two years. tuition at the college is $6,900 each year and it's earned a one-time scholarship for $2,500 he expects to earn $2,000 each year at his part-time job his parents have promise to pay the rest of his tuition how much money will earn his parents pay for two years of tuition
Answers
Answer:
7,300
Step-by-step explanation:
6900x2 years=13,800 total tuition.
13800-2500-4000 (2000x2)=7,300
Magan decides to research the relationship between the length in inches and the
weight of a certain species of catfish. He measures the length and weight of a number
of specimens he catches, then throws back into the water. After plotting all his data,
he draws a line of best fit. Based on the line of best fit, what would you predict to be
the length of a catfish that weighed 40 pounds?
Answers
Based on the line of best fit, the length of this catfish can be predicted to be 38 inches.
Given the following data:
Weight of catfish, x = 40 pounds.What is a line of best fit?A line of best fit is also referred to as a trend line and it can be defined as a statistical (analytical) tool that is used in conjunction with a scatter plot, in order to determine whether or not there's any correlation between a data.
From the graph of the data, we have the following linear equation:
\(y=\frac{1}{2} x+18\)
Substituting the value of x, we have:
\(y=(\frac{1}{2} \times 40 )+18\\\\y=20+18\)
y = 38 inches.
Read more on scatterplot here: https://brainly.com/question/6592115

make e the subject
e-5=2f
Answers
Answer:
e-5=2f
take '-5' to the other side where '2f' is
e=2f+5
greater than equal to
greater than
less than equal to
less than

Answers
Answer:
Step-by-step explanation:
greater than or equal to
In class, we developed the formula
(a) Use the formula (using appropriate substitutions) to find the closed form for ∑2
= 2
(b) Use the formula in the notes for ∑
= 13 to find the closed form expression form for
∑
= 3 (assume a ≥ 1 and a ≤ b)
(c) In class, we developed the formula
Use this formula and some algebra to derive a closed form for the sum ∑
= 0( ― 1)2 ― 1
(d) Test your closed form solution in (c) to find the value of ∑3
= 0( ― 1)2 ― 1 and see if
it matches the manual computation of the 4 terms of the sum.
Answers
(a) The closed form for ∑2 is 2.
(b) The closed form expression for ∑3 is 24.
(c) The closed form for the sum ∑n = 0(― 1)² ― 1 is n(1 - n) / 2.
(d) The value of -3 matches the manual computation of the four terms.
Our closed form solution is correct.
To find the closed form for ∑2, we can use the formula for the sum of the first n terms of an arithmetic series:
∑2 = n(a + l) / 2
In this case, a = 2 (the first term) and l = 2 (the last term) since we are summing a series of 2's.
We also know that there is only one term, so n = 1.
Substituting these values into the formula, we have:
∑2 = 1(2 + 2) / 2
= 4 / 2
= 2
The formula for the sum of the first n terms of an arithmetic series is:
∑n = n(a + l) / 2
In this case, we have a = 3 (the first term), l = 13 (the last term), and n = 3 (the number of terms).
Substituting these values into the formula, we get:
∑3 = 3(3 + 13) / 2
= 3(16) / 2
= 48 / 2
= 24
The formula we developed in class is:
∑n = n(a + a + (n - 1)d) / 2
In this case, we have a = 0 (the first term) and d = -1 (the common difference).
Substituting these values into the formula, we get:
∑n = n(0 + 0 + (n - 1)(-1)) / 2
= n(0 - n + 1) / 2
= n(1 - n) / 2
To test the closed form solution for ∑3 = 0(― 1)² ― 1, we substitute n = 3 into the closed form expression we derived in part (c):
∑3 = 3(1 - 3) / 2
= 3(-2) / 2
= -6 / 2
= -3
Now, let's manually compute the sum of the first four terms of ∑3 = 0(― 1)² ― 1:
0(― 1)² ― 1 + 1(― 1)² ― 1 + 2(― 1)² ― 1 + 3(― 1)² ― 1
= 0 - 1 - 2 - 3
= -6
For similar questions on manual computation
https://brainly.com/question/32637761
#SPJ8