Answers
\(\huge \bf༆ Answer ༄\)
Let's solve ~
\({ \qquad{ \sf{ \dashrightarrow}}} \: \: \sf \:7 \sec(x) - 7 = 0\)
\({ \qquad{ \sf{ \dashrightarrow}}} \: \: \sf \:7 \sec(x) = 7\)
\({ \qquad{ \sf{ \dashrightarrow}}} \: \: \sf \: \sec(x) = 7 \div 7\)
\({ \qquad{ \sf{ \dashrightarrow}}} \: \: \sf \: \sec(x) = 1\)
\({ \qquad{ \sf{ \dashrightarrow}}} \: \: \sf \:x = 0\)
Related Questions
Question:-
The area of two similar triangles are 81 cm2 and 49 cm² respectively. If one of the sides of the first triangle is 6.3 cm, find the corresponding side of the other triangle.
Answers
Let's assume that the corresponding side of the second triangle is \(\displaystyle\sf x\).
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can set up the following proportion:
\(\displaystyle\sf \left( \dfrac{x}{6.3} \right)^{2} =\dfrac{49}{81}\)
To find \(\displaystyle\sf x\), we can solve the proportion above:
\(\displaystyle\sf \left( \dfrac{x}{6.3} \right)^{2} =\dfrac{49}{81}\)
Taking the square root of both sides:
\(\displaystyle\sf \dfrac{x}{6.3} =\sqrt{\dfrac{49}{81}}\)
Simplifying the square root:
\(\displaystyle\sf \dfrac{x}{6.3} =\dfrac{7}{9}\)
Cross-multiplying:
\(\displaystyle\sf 9x = 6.3 \times 7\)
Dividing both sides by 9:
\(\displaystyle\sf x = \dfrac{6.3 \times 7}{9}\)
Calculating the value:
\(\displaystyle\sf x = 4.9\)
Therefore, the corresponding side of the second triangle is \(\displaystyle\sf 4.9 \, cm\).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Answer:
Step-by-step explanation:
let's assume that the corresponding side of the second triangle is .
The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Therefore, we can set up the following proportion:
To find , we can solve the proportion above:
Taking the square root of both sides:
Simplifying the square root:
Cross-multiplying:
Dividing both sides by 9:
Calculating the value:
Therefore, the corresponding side of the second triangle is 4.9cm
hope it helped u dear...........
How many cubic blocks of side length
7 inch would it take to fill a
3
cube with a side length of 7 Inch?
Plato User.
Is it:
A. 27
B. 4
C. 3
Thanks!
Answers
Answer:
b because you sub the 2 numbers i think
E U F {2,4,6,8,} true or false
Answers
A cake recipe calls for 125grams of butter Juan's dad says they haye 0.2 kilograms of butter Do they have enough butter to make the cake
Answers
Answer:
Yes
Step-by-step explanation:
125 grams is 0.125 kilograms, 0.125 < 0.2
Find the equation of a line parallel to y=x−1 that contains the point (−3,−2). Write the equation in slope-intercept form.
Answers
Answer:
y = x + 1
Step-by-step explanation:
Parallel lines have same slope.
y = x - 1
Compare with the equation of line in slope y-intercept form: y = mx +b
Here, m is the slope and b is the y-intercept.
m =1
Now, the equation is,
y = x + b
The required line passes through (-3 ,-2). Substitute in the above equation and find y-intercept,
-2 = -3 + b
-2 + 3 = b
\(\boxed{b= 1}\)
Equation of line in slope-intercept form:
\(\boxed{\bf y = x + 1}\)
The equation is :
↬ y = x + 1Solution:
We KnowIf two lines are parallel to each other, then their slopes are equal. The slope of y = x - 1 is 1. Hence, the slope of the line that is parallel to that line is 1.
We shouldn't forget about a point on the line : (-3, -2).
I plug that into a point-slope which is :
\(\sf{y-y_1=m(x-x_1)}\)
Slope is 1 so
\(\sf{y-y_1=1(x-x_1)}\)
Simplify
\(\sf{y-y_1=x-x_1}\)
Now I plug in the other numbers.
-3 and -2 are x and y, respectively.
\(\sf{y-(-2)=x-(-3)}\)
Simplify
\(\sf{y+2=x+3}\)
We're almost there, the objective is to have an equation in y = mx + b form.
So now I subtract 2 from each side
\(\sf{y=x+1}\)
Hence, the equation is y = x + 1which point is on the line 4y-2x=0
Answers
Answer:
(2,1)
Step-by-step explanation:
The line 4y - 2x = 0 can be written in slope-intercept form as y = 1/2x.
So any point that satisfies this equation will lie on the line. For example, the point (2,1) satisfies the equation:
4(1) - 2(2) = 0
So the point (2,1) is on the line.
heheheheh hehehehehhehehehehehehheheh
Answers
Answer:
cscsc
Step-by-step explanation:
zcscc
Answer:
hehehehehehehehehehehehehehehehehehehehehehehehe
Step-by-step explanation:
lelelelelelelelelelelelelelelelelelelelelelelelelelelelelelelelelelele
Chicken Nuggets.
The units of an item available for sale during the year were as follows: Jan. 1 Inventory 50 units at $124 Mar. 10 Purchase 60 units at $132 Aug. 30 Purchase 20 units at $138 Dec. 12 Purchase 70 units at $142 There are 80 units of the item in the physical inventory at December 31. The periodic inventory system is used. Determine the ending inventory cost and the cost of goods sold by three methods. Round interim calculations to one decimal and final answers to the nearest whole dollar. blank Cost of Ending Inventory and Cost of Goods Sold Inventory Method Ending Inventory Cost of Goods Sold First-in, first-out (FIFO) $fill in the blank 1 $fill in the blank 2 Last-in, first-out (LIFO) fill in the blank 3 fill in the blank 4 Weighted average cost fill in the blank 5 fill in the blank 6
Answers
Ending Inventory Cost and Cost of Goods Sold using different inventory methods:
FIFO Method:
Ending Inventory Cost: $11,920
Cost of Goods Sold: $15,068
LIFO Method:
Ending Inventory Cost: $11,996
Cost of Goods Sold: $15,123
Weighted Average Cost Method:
Ending Inventory Cost: $11,974
Cost of Goods Sold: $15,087
Using the FIFO (First-In, First-Out) method, the cost of the ending inventory is determined by assuming that the oldest units (those acquired first) are sold last. In this case, the cost of the ending inventory is calculated by taking the cost of the most recent purchases (70 units at $142 per unit) plus the cost of the remaining 10 units from the March 10 purchase.
This totals to $11,920. The cost of goods sold is calculated by taking the cost of the units sold (50 units from the Jan. 1 inventory at $124 per unit, 60 units from the March 10 purchase at $132 per unit, and 20 units from the August 30 purchase at $138 per unit), which totals to $15,068.
Using the LIFO (Last-In, First-Out) method, the cost of the ending inventory is determined by assuming that the most recent units (those acquired last) are sold first. In this case, the cost of the ending inventory is calculated by taking the cost of the remaining 10 units from the December 12 purchase, which amounts to $1,420, plus the cost of the 70 units from the August 30 purchase, which amounts to $10,576.
This totals to $11,996. The cost of goods sold is calculated by taking the cost of the units sold (50 units from the Jan. 1 inventory, 60 units from the March 10 purchase, and 20 units from the August 30 purchase), which totals to $15,123.
Using the Weighted Average Cost method, the cost of the ending inventory is determined by calculating the weighted average cost per unit based on all the purchases. In this case, the total cost of all the purchases is $46,360, and the total number of units is 200.
Therefore, the weighted average cost per unit is $231.80. Multiplying this by the 80 units in the physical inventory at December 31 gives a total cost of $11,974 for the ending inventory. The cost of goods sold is calculated by taking the cost of the units sold (50 units from the Jan. 1 inventory, 60 units from the March 10 purchase, and 20 units from the August 30 purchase), which totals to $15,087.
for such more questions on Cost
https://brainly.com/question/2292799
#SPJ8
least common number
( sorry i forgot what its called )
of 598 and 45
Answers
The least common multiple of 598 and 45 is 26, 910
How to find the least common multiple ?To find the least common multiple of 598 and 45, you can use the prime factorization method. This involves finding the prime factors of both 598 and 45 and then multiplying these prime factors when they are in their highest power.
This gives:
598 prime factorization :
2 x 13 x 23 = 598
45 prime factorization :
3 x 3 x 5 = 45
The least common multiple is;
= 2 x 13 x 23 x 3 x 3 x 5
= 26, 910
Find out more on least common multiple at https://brainly.com/question/233244
#SPJ1
What is the area of the kite
20 square meters
36 square meters
40 square meters
80 square meters

Answers
Answer:
C
Step-by-step explanation:
Answer:
It is c / 40 square meters
Step-by-step explanation:
I took the test
150 adults compleate a survay 80 are women
Answers
Mark me as Brainly

Which of the following are solutions to the quadratic equation below?
Check all that apply.
x²+7x-8=0
A. -1
B. 2
C. -4
D. -8
E. 1

Answers
Therefore, the solutions to the quadratic equation x² + 7x - 8 = 0 are -8 and 1. The answers are D and E.
What is equation?An equation is a mathematical statement that shows that two expressions are equal. It typically consists of variables, constants, and mathematical operations. Equations can be solved by manipulating the expressions to find the value of the variables that satisfy the equation. Equations can be used to model real-world situations, and they are an important tool in many fields, including mathematics, physics, engineering, and economics.
Here,
To check which values are solutions to the quadratic equation, we can substitute each value into the equation and see if it equals zero.
Substituting -1 into the equation:
(-1)² + 7(-1) - 8 = 1 - 7 - 8 = -14, which is not equal to zero.
Substituting 2 into the equation:
2² + 7(2) - 8 = 4 + 14 - 8 = 10, which is not equal to zero.
Substituting -4 into the equation:
(-4)² + 7(-4) - 8 = 16 - 28 - 8 = -20, which is not equal to zero.
Substituting -8 into the equation:
(-8)² + 7(-8) - 8 = 64 - 56 - 8 = 0, which is equal to zero. Therefore, -8 is a solution to the equation.
Substituting 1 into the equation:
1² + 7(1) - 8 = 1 + 7 - 8 = 0, which is equal to zero. Therefore, 1 is a solution to the equation.
To know more about equation,
https://brainly.com/question/28243079
#SPJ1
Part A: Timothy said that AKLM was dilated by a scale factor of 1.5 centered at the origin. Is Timothy CORRECT? Explain your answer or show your work.

Answers
Yes, Timothy is correct because triangle AKLM was dilated by using a scale factor of 1.5 centered at the origin.
What is dilation?In Mathematics, dilation can be defined as a type of transformation that is typically used for enlarging or reducing the size of a geometric object but not its shape, based on the scale factor.
For the given coordinates of the preimage triangle KLM, the dilation with a scale factor of 1.5 from the origin (0, 0) would be calculated as follows:
Coordinate K (-1, 3) → Coordinate K' (-1 × 1.5, 3 × 1.5) = Coordinate K' (-1.5, 4.5).
Coordinate L (8, 4) → Coordinate L' (8 × 1.5, 4 × 1.5) = Coordinate L' (12, 6).
Coordinate M (10, -3) → Coordinate M' (10 × 1.5, -3 × 1.5) = Coordinate M' (15, -4.5).
In conclusion, the coordinates of the image triangle K'L'M after a dilation with a scale factor of 1.5 from the origin are (-1.5, 4.5), (12, 6), and (15, -4.5) as shown in the graph above, therefore, Timothy is correct.
Read more on dilation here: brainly.com/question/20482938
#SPJ1
solve this equation, and show work. worth 40 points.

Answers
Answer:
\(r=-3/5=-0.6\)
Step-by-step explanation:
We have the equation:
\(6^{-3r}=6^{2r+3}\)
Since their bases are the same, the exponents must be equivalent. So:
\(-3r=2r+3\)
Solve for r, subtract 2r from both sides:
\(-5r=3\)
Divide both sides by -5:
\(r=-3/5=-0.6\)
So, the value of r is -3/5.
And we're done!
a car travels 224 miles in 3 hours and 30 minutes. how many miles does it travel per hour
Answers
Answer:
64 miles per hour.
Step-by-step explanation:
we are asked to look for the velocity of this car. to find it, we use the equation \(velocity = \frac{distance}{time}\). we substitute the given to the equation:
\(velocity = \frac{224 m}{3.5 hr}\)
velocity = 64 miles per hour
help
\(3( \frac{27}{8} ) ^{ \frac{2}{3} x - 1} =2( \frac{32}{243} ) ^{ {2} x }\)
I need help with this ASAP
![help[tex]3( \frac{27}{8} ) ^{ \frac{2}{3} x - 1} =2( \frac{32}{243} ) ^{ {2} x }[/tex]I need help with](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/GrtgDOnuxD0qUu5iQgbmdcybzoXEWHLW.jpeg)
Answers
\(\huge\fbox{Answer ☘}\)
\(\bold{3( \frac{27}{8} ) {}^{ \frac{2}{3} \times - 1} = 2( \frac{32}{243} ) {}^{2x} }\\ \\3(( \frac{3}{2} ) {}^{3} ) {}^{ \frac{2}{3} \times - 1 } = 2(( \frac{2}{3} ) {}^{5} ) {}^{2x} \\\\ 3( \frac{3}{2} ) {}^{2 \times - 1} = 2( \frac{2}{3} ) {}^{10x} \\\\ 3( \frac{2}{3} ) {}^{2} = 2( \frac{2}{3} ) {}^{10x} \\\\
3( \frac{4}{9} ) = 2( \frac{4}{9} ) {}^{5x} \\\\\bold\pink{ comparing \: powers }\\\\5x = 1 \\\\ \bold\blue{x = \frac{1}{5} } \)
hope helpful~
А 10 0 B В 1) Which one of these shapes is not like the others?

Answers
In order to compare the figures and find the one that is not like the others, let's compare the proportion of their width and height:
\(\begin{gathered} A\colon \\ \frac{\text{width}}{\text{height}}=\frac{5}{4} \\ \\ B\colon \\ \frac{\text{width}}{\text{height}}=\frac{10}{8}=\frac{5}{4} \\ \\ C\colon \\ \frac{\text{width}}{\text{height}}=\frac{10}{6}=\frac{5}{3} \end{gathered}\)We can see that figure C has a different proportion, therefore figure C is the one that is not like the others.
21x² - 2x + 1/2 =0
find the following quadratic equation by factorization method
PLESE SOMEONE HELP
Answers
Step-by-step explanation:
21x²-2x +1/2 = 0
x² - 2x ×21 + 1/2× 21 = 0
The table represents a linear relationship
X—2 0 4
Y-4 3 1
Which equation represents the table
Y=1/2x+5
y=-1/2x+3
Y=2x-3
Y=-4x+2
Answers
The linear relationship illustrated in the provided table can be effectively described by the equation Y = -4x + 2. Option D.
To determine the equation that represents the given table with the values of x and y, we can observe the pattern and find the equation of the line that fits these points.
Given the table:
X: 2 0 4
Y: -4 3 1
We can plot these points on a graph and see that they form a straight line.
Plotting the points (2, -4), (0, 3), and (4, 1), we can see that they lie on a line that has a negative slope.
Based on the given options, we can now evaluate each equation to see which one represents the line:
Y = 1/2x + 5
When we substitute the x-values from the table into this equation, we get the following corresponding y-values: -3, 5, and 6. These values do not match the given table, so this equation does not represent the table.
Y = -1/2x + 3
When we substitute the x-values from the table into this equation, we get the corresponding y-values: 4, 3, and 2. These values also do not match the given table, so this equation does not represent the table.
Y = 2x - 3
When we substitute the x-values from the table into this equation, we get the corresponding y-values: -4, -3, and 5. These values do not match the given table, so this equation does not represent the table.
Y = -4x + 2
When we substitute the x-values from the table into this equation, we get the corresponding y-values: -6, 2, and -14. Interestingly, these values match the y-values in the given table. Therefore, the equation Y = -4x + 2 represents the table.
In conclusion, the equation Y = -4x + 2 represents the linear relationship described by the given table. So Option D is correct.
For more question on equation visit:
https://brainly.com/question/29174899
#SPJ8
Finding the Midpoint of a Line
Segment
To find the midpoint, M, of AB we can use
formula for finding point C. This works
because the M lies along AB and divides it in
a fixed ratio. So, if the midpoint of AB is point M, what must the ratio of a : b be? Since we know the ratio of a to b, we can substitute the values you wrote above back into the formula for finding a point along a line segment.

Answers
Francis wanted to purchace a new tablet. Egar's electronic offered a savings of 25% on a tablet originally costing $499. How much will Francis pay for this product?
Answers
Given data:
The given discount is D=25%.
The original cost of tablet is T=$499.
The expression for the final amount is,
A=(100%-D)(T)
Substitute the given values in the above expression.
A=(100%-25%)($499)
=(75%)(499)
=(0.75)(499)
=$374.25
Thus, the finl price to be paid is $374.25.
True or False? A circle could be circumscribed about the quadrilateral below.

Answers
Yes, A circle could be circumscribed about the quadrilateral below.
What is circle?A circle is a closed two-dimensional figure in which the set of all the points in the plane is equidistant from a given point called “centre”. The perimeter around the circle is known as the circumference.
here, we have,
A circle can be circumscribed around the four vertices of a quadrilateral
if and only if,
both pair of opposite angles inscribed in the quadrilateral are supplementary to each other.
By supplementary to each other we mean that their sum is equal to 180°.
we have,
In this case we have opposite interior angles supplementary to each other hence we can circumscribe a circle around it.
Such Quadrilateral are called cyclic quadrilateral.
Hence, Yes, A circle could be circumscribed about the quadrilateral below.
Learn more about circle here:
brainly.com/question/11833983
#SPJ7
The scatterplot above displays the relationship between the amount of food hippopotamuses eat per day and their age. Describe and explain any associations and data features on the scatterplot. Then, use the variables on the graph to interpret the relationship that is shown.

Answers
The scatter plot shows a [positive linear] association.
How to determine the association of the scatterplotFrom the question, we have the following parameters that can be used in our computation:
The image of the scatter plot
On the scatter plot, we can see that
The points appear to be on a straight line
Also, we can see that
As the x values increases the y values increases
This represents a positive linear association.
Hence, the association is a positive linear association.
Read more about scatter plot at
brainly.com/question/16920148
#SPJ1
Solve for x.
−12(x+2)+112x=3
x = 1
x = 2
x = 4
x = 5
Answers
Answer:
x=1 maybe ,but I am not sure for this answer.
Answer: It's X = 4
Step-by-step explanation:
I just took the test and got x = 1 wrong
Need help. This please

Answers
The domain of the quadratic function in this problem is given as follows:
All real values.
How to obtain the domain of the function?The domain of a function is the set of all the possible input values that can be assumed by the function.
On the graph, the domain of the function is given by the values of x of the function.
A quadratic function has no restrictions on the domain, hence it is defined by all the real values.
More can be learned about the domain of a function at https://brainly.com/question/10687170
#SPJ1
Explain how you can find the y-intercept of a function when given an equation of a graph.

Answers
The y-intercept of a function is the value of y when x = 0, which is represented as the value of b in the slope-intercept equation y = mx + b. b is the y-intercept.
What is the Y-intercept of a Function?If an equation of graph that represents a function is given in slope-intercept form as y = mx + b, the value of b in the function is the value of the y-intercept of the y-intercept.
The y-intercept of the function is the same as the value of y when the value of x is 0, or the point where the line of the function intercepts the y-axis on a given graph that represents the function.
For example, if we are given the equation of a graph that represents a function as, y = 3x + 4, the y-intercept of the function would be 4.
In summary, the y-intercept of the function is the value of b in the equation of the function that is expressed as y = mx + b in slope-intercept form.
Learn more about the y-intercept of function on:
https://brainly.com/question/15602982
#SPJ1
On the Moon, an astronaut will have______mass and________.
weight as on Earth
A. 1/6th the, the same
B. the same, 1/6th the
C. 1/6th the, 1/6th the
D. the same, the same
Answers
Answer:
B
Step-by-step explanation:
Answer:
D. Because the same answer
Step-by-step explanation:
Mark used 14 bananas, 15 oranges, and 24 strawberries in his fruit salad.
Dani used 7 bananas, 9 oranges, and 12 strawberries. Did Mark and Dan
use the same ratio of bananas to strawberries? *
Answers
Answer:
yes-
Step-by-step explanation:
im not to sure if its right but
7+7=14
12+12=24
Find the measure of angle A.
60x
O 60°
O 30°
O 23°
O 37°
30x
A

Answers
Answer:
Step-by-step explanation:
sum of angles in a triangle=180º
90+60x+30x=180
90+90x=180
90(1+x)=180
1+x=2
x=1
angle A=30º
Construct parametric equations describing the graph of the following equation.y = 4x - 3If y = 1-5, find the parametric equation for x,
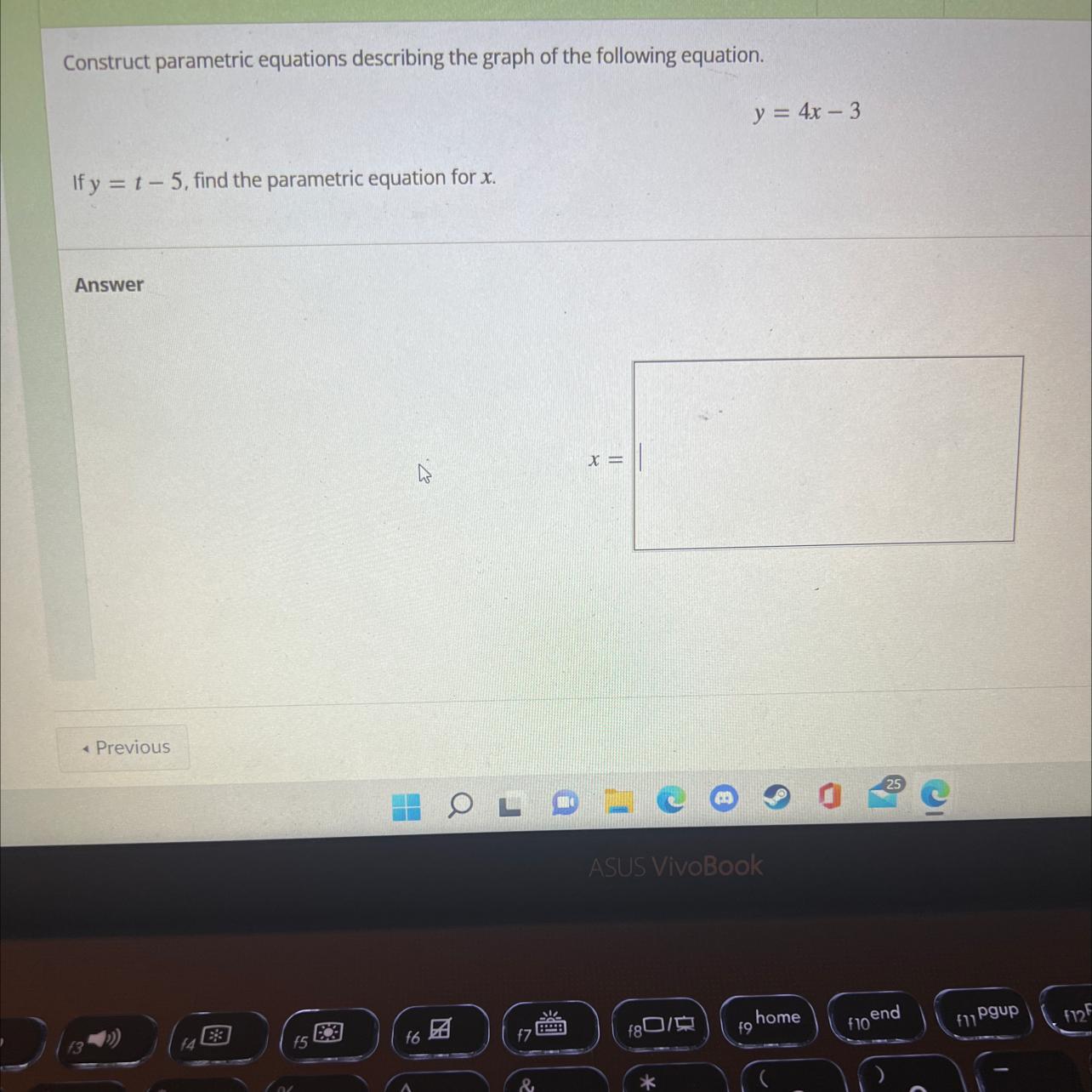
Answers
Let us begin by defining important terms:
A rectangular equation, or an equation in rectangular form is an equation composed of variables like x and y which can be graphed on a regular Cartesian plane. For example y=4x+3 is a rectangular equation.
A curve in the plane is said to be parameterized if the set of coordinates on the curve, (x,y) , are represented as functions of a variable t .
x=f(t)
y=g(t)
Given:
The rectangular equation is defined as:
\(y\text{ = 4x - 3}\)If y = t -5
The parametric equation for x is obtained by substitution:
\(\begin{gathered} t\text{ -5 = 4x - 3} \\ Make\text{ x the subject of formula} \\ 4x\text{ = t - 5 + 3} \\ 4x\text{ = t - 2} \\ Divide\text{ both sides by 4} \\ x\text{ = }\frac{t-2}{4} \end{gathered}\)Hence, the parametric equation for x is:
\(x\text{ = }\frac{t-2}{4}\)