Solve tan(x) (tan x + 1) = 0. O A. X = int.x = ** OB. B. x = 3 + 27T9,X = 37 + 277 4 O ETN C. X = }T, X = ? + T1 O EX= D. X = +17,X = +277 2
Answers
we have the equation
tan(x) (tan x + 1) = 0
this equation is satisfied when
tan(x)=0
and
(tanx+1)=0
Remember that
the tanx is zero when the sine is zero
so
x=0,pi, 2pi,3pi,...
x=(+/-)npi
and
(tanx+1)=0
when
the value of tanx=-1
so
x=-pi/4 --------> pi/4(+/-)npi
therefore
the answer is option ARelated Questions
Consider an inductive definition of a version of Ackermann's function. This function was named after Wilhelm Ackermann, a German mathematician who was a student of the great mathematician David Hilbert. Ackermann's function plays an important role in the theory of recursive functions and in the study of the complexity of certain algorithms involving set unions. (There are several different variants of this function. All are called Ackermann's function and have similar properties even though their values do not always agree.) if m 0 if m 2 1, n 0 ifm2 1,n 1 if m21, n22 2n 0, A (m,n) 2 A (m-1, A (m,n 1) Find these values of Ackermann's function. A (2, 2) Multiple Choice 4 by the fourth line of the definition 4 by the first line of the definition 2 by the third line of the definition O by the second line of the definition
Answers
The value of A(2,2) is not 4, but rather 65536, which is obtained by using the recursive definition of the function.
The given inductive definition of Ackermann's function is used to calculate the values of the function for given input values of m and n. The definition uses recursive steps to define the function for different values of m and n. To find the value of A(2,2), we start with the base cases, which are given by the first two lines of the definition. Here, since m=2 and n=2, we use the third line of the definition, which gives the value 2n=2x2=4. Now, we use the fourth line of the definition to compute A(2,1) by using the value of A(2,2) that we just found. This gives us A(2,1)=\(2^4\)=16. Finally, we use the fourth line of the definition once again to compute A(2,0) by using the value of A(2,1) that we just found. This gives us A(2,0)=\(2^{16}\)=65536. Therefore, the value of A(2,2) is not 4, but rather 65536, which is obtained by using the recursive definition of the function.
To learn more about function:
https://brainly.com/question/12431044
#SPJ4
2x² + 5x, what will it a Perfect Square? make
Answers
Answer:
2x² + 5x + c = 0
For this quadratic equation to have one double root, the discriminant must equal 0.
5² - 4(2)(c) = 0
25 - 8c = 0
c = 25/8
2x² + 5x is not a perfect square because the coefficient of x², 2, is not a perfect square.
Explanation:2x² + 5x is not a perfect square.
A perfect square is an expression that can be factored into the square of a binomial. To determine if an expression is a perfect square, we can look at the coefficient of x². In this case, the coefficient is 2, which is not a perfect square.Learn more about Perfect Square here:https://brainly.com/question/34063927
#SPJ11
PLEASE HELP
I need this done is 13 minutes.
Polygon ABCD with vertices at A(1,-1) B(3,-1), C(3,-2) and D(1-2) is dilated to create polygon ABCD with vertices at A’(2,-2), B(6,-2), C’(6,-4) and D’(2,-4). Determine the scale factor used to create the image
A. 3
B. 2
C. 1/2
D. 1/3
Answers
The correct answer is B. 2, as the scale factor used to create the dilated polygon is 2.
To determine the scale factor used to create the image, we can compare the corresponding side lengths of the original polygon ABCD and the dilated polygon A'B'C'D'.
Let's calculate the lengths of the corresponding sides:
Side AB: The length of side AB is 3 - 1 = 2 units in the original polygon. In the dilated polygon, the length of side A'B' is 6 - 2 = 4 units.
Side BC: The length of side BC is -2 - (-1) = -1 units in the original polygon. In the dilated polygon, the length of side B'C' is -4 - (-2) = -2 units.
Side CD: The length of side CD is 1 - 3 = -2 units in the original polygon. In the dilated polygon, the length of side C'D' is 2 - 6 = -4 units.
Side DA: The length of side DA is -1 - (-2) = 1 unit in the original polygon. In the dilated polygon, the length of side D'A' is -2 - (-4) = 2 units.
Now, let's compare the corresponding side lengths:
AB: A'B' = 4 units / 2 units = 2
BC: B'C' = -2 units / -1 units = 2
CD: C'D' = -4 units / -2 units = 2
DA: D'A' = 2 units / 1 unit = 2
The scale factor used to create the image is the ratio of the corresponding side lengths.
In this case, all the corresponding side lengths have a ratio of 2.
For similar question on scale factor.
https://brainly.com/question/30581940
#SPJ8
1. 543.5 = _______ ft _________ in
Answers
Answer:
uważam że nie wiem ale bym wiedział tylko muszę wiedzieć
Supplies for last year cost $1,477, which was $177 over budget. Rounded to the nearest 1%, by what percent did the cost exceed the budgeted cost?
8%
11%
12%
13%
14%
Answers
Answer:
12% is the correct answer.
You took 6 math quizzes. Your scores are: 89, 96, 92, 84, 94, 100. Mrs. Edwards gave you the choice to pick the mean, median, mode or range to be your report card grade. Which one would you pick and why?
Answers
Answer:
Median. It has the highest grade.
Step-by-step explanation:
Mean: 92.5
Median: 93
Mode: no mode (all numbers occur only once)
Range: range is 11 (this would be a terrible grade)
Because the median has the highest grade, you would want to pick it.
If you want/ need me to show work or explain just let me know
Also, if my answer helps please consider giving me brainliest.
Identify the pair of angles as complementary, supplementary, or neither.
PLEASE HELP

Answers
Answer:
supplementary
Step-by-step explanation:
135 + 45 = 180
supplementary angle ALWAYS add up to 180.
Can some one please help me

Answers
Answer:
A is the answer
Step-by-step explanation:
If the relative frequencies being compared are 0.21 and
0.79, which conclusion is most likely supported by the
data?
Answers
Answer: Option Option (B)
(B) There is likely an association between the categorical variables because the relative frequencies are not similar in value. <======+ 100%
Step-by-step explanation: Question?
.- A conditional relative frequency table is generated by column from a set of data. The conditional relative frequencies of the two categorical variables are then compared.
If the relative frequencies being compared are 0.21 and 0.79, which conclusion is most likely supported by the data?
The conclusion that should be supported is there is an association that lies between the categorical variables since the relative frequencies are not similar in value.
What is a conditional relative frequency table?It is produced by the column form for setting out the data. It is of the two categorical variables that made for comparison.
In the case when the relative frequencies being compared are 0.21 and
0.79 so the above conclusion should be considered.
learn more about frequencies here: https://brainly.com/question/24559701
Find the volume of a cone with radius 5 yards and height 8 yards. Round your answer to two
decimal places
Answers
The volume of a cone will be 209.41 yard³.
What is volume of cone?
The area or volume that a cone takes up is referred to as its volume. Cones are measured by their volume in cubic units such as cm3, m3, in3, etc. By rotating a triangle at any of its vertices, a cone can be created. A cone is a robust, spherical, three-dimensional geometric figure.. Its surface area is curved. The perpendicular height is measured from base to vertex. Right circular cones and oblique cones are two different types of cones. While the vertex of an oblique cone is not vertically above the center of the base, it is in the right circular cone where it is vertically above the base.
So the
V = (1/3)πr²h.
Given, data r = 5yards
h = 8 yards
Volume = 1/3 * π * r ²* h
= 1/3 * 3.141*25*8
=209.41 yard³
Hence, the volume of a cone will be 209.41 yard³.
Learn more about volume of cone, by the following link
https://brainly.com/question/1082469
#SPJ1
Mr Kenny brought a new plant. The plant grew 2.6 centimeters in the first week and 3.42 centimeters the second week Select all the true comparisons of the plant growth for the two weeks

Answers
Given data:
The growth in first week is a=2.6 cm.
The growth in second week is b=3.42 cm.
3.42>2.6
Thus, the option second and option third is correct.
A linear system of equations that is said to be consistent has how many solutions?
Answers
A linear system of equations that is said to be consistent is when you have a solution for this system but also you can have an inifinity number of solutions.
the system is incosistent when this systems don't have a solution.
Complete the following statement. Use the integers that are closest to the number in the
middle.
<- √54<
Submit
I don't know this yet
Answers
First Box=-4 Second Box=-3
Step-by-step explanation:
Please help me ASAP please I need help
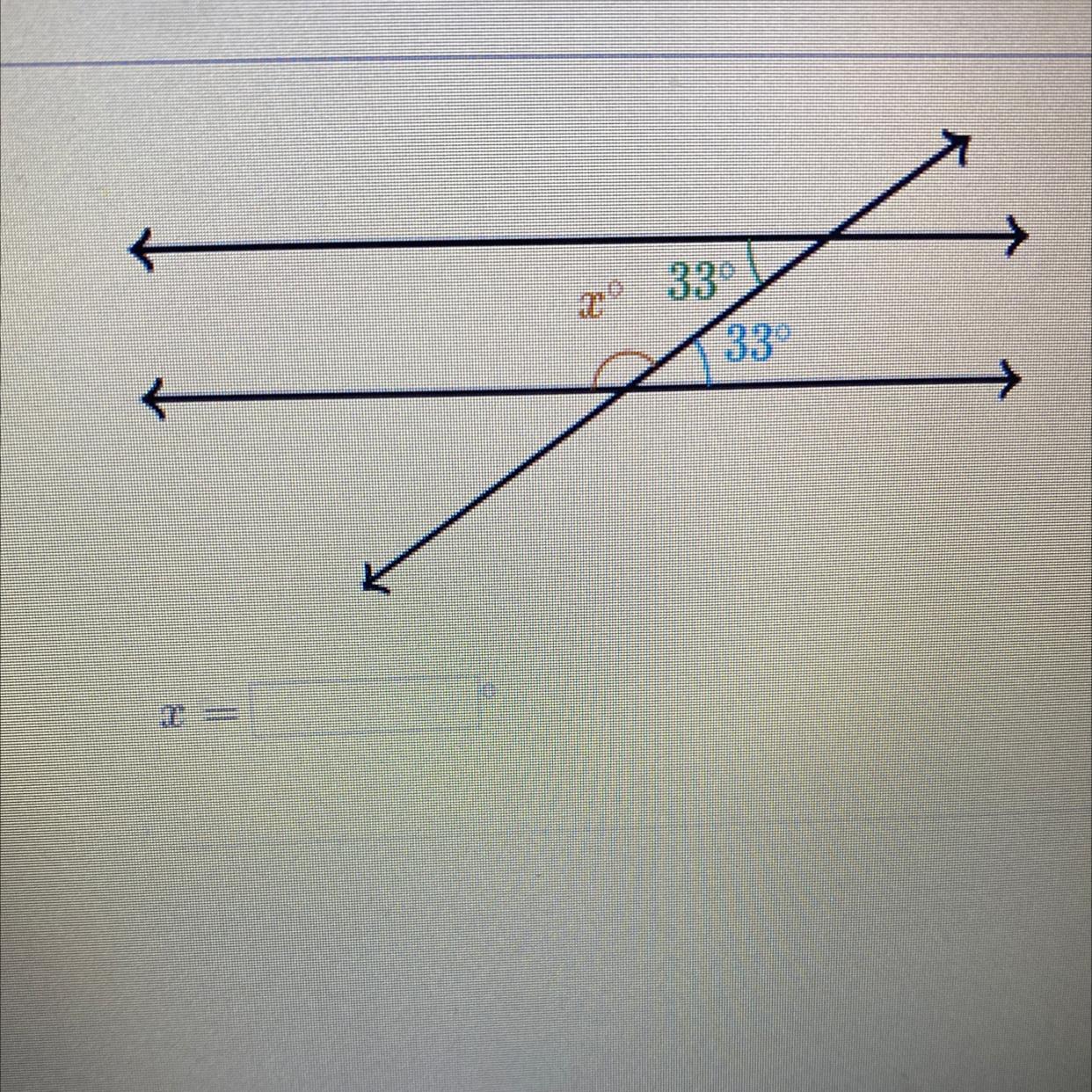
Answers
Answer:
147°
Step-by-step explanation:
Solving for x
To make a straight line the angles have to have a sum of 190. So 180°-33° would equal 147°
Answer:
x = 147°
Step-by-step explanation:
A line is 180°
180 - 33 = 147
Find the area of the rectangle on this centimetre grid.
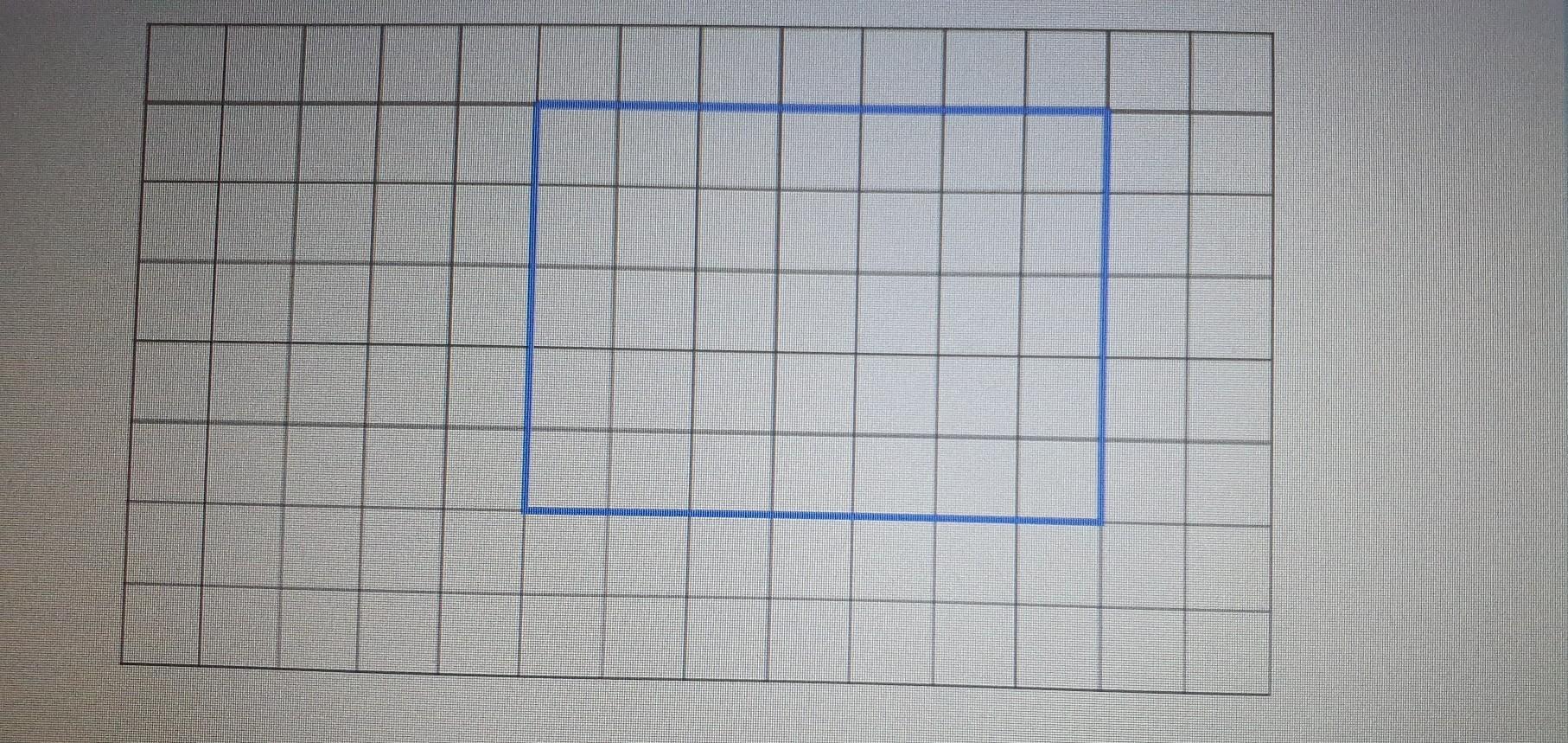
Answers
Answer:
A = 35 cm²
Step-by-step explanation:
the area (A) of a rectangle is calculated as
A = length × width
by counting the squares on the sides
length = 7 cm and width = 5 cm , then
A = 7 × 5 = 35 cm²
need Answer to these questions. pls help

Answers
Answer:
7.2 million dollars
Step-by-step explanation:
The domain of the function the complete set of possible values of the independent variable. In this case the domain includes all real numbers except 189.
From;
T(p) = 0.50 (p - 189)
When p = 203.4 million dollars
T(p) = 0.50 (203.4 - 189)
T(p) = 7.2 million dollars
A shopping centre wants to examine the amount of space required for parking. Studies indicated that 50% of staff and shoppers use public transportation. A survey of 1002 was taken, and 483 responded that they used public transportation. At 5% level of significance, is it reasonable to conclude that the survey results indicate a change?
Answers
Answer:
The survey result doesn't indicate the change
Step-by-step explanation:
Previous study result is 50%
Survey result:
483/1002 = 0.482 = 48.2%Comparing with previous result:
50% - 48.2% = 1.8% < 5%Since this result is within 5% level of significance, it can be concluded that the survey result doesn't indicate the change
A sample of 100 women is obtained, and their heights (in inches) and pulse rates (in beats per minute) are measured. The linear correlation coefficient is 0.239 and the equation of the regression line is y = 18.5 + 0.890x, where x represents height. The mean of the 100 heights is 62.9 in and the mean of the 100 pulse rates is 73.4 beats per minute. Find the best predicted pulse rate of a woman who is 65 in tall. Use a significance level of α=0.01 The best predicted pulse rate of a woman who is 65 in tall is_______beats per minute.. (Round to two decimal places as needed.) Answer
Answers
Answer:
54.07 inches
Step-by-step explanation:
Given the regression equation :
y = 18.5 + 0.890x
y = pulse rate in beats per minute
x = height
The best predicted pulse rate of a woman who is 65 inches
Put y = 65 in the regression equation :
65 = 18.5 + 0.890x
65 - 18.5 = 0.890x
46.5 = 0.890x
Divide both sides by 0.890
46.5 / 0.890 = 0.890x / 0.890
54.0697 = x
The best predicted pulse rate for a woman wo is 65 inches tall is 54.07 inches
round 5.638 to the nearrest tenth
Answers
Answer:
5.6
Step-by-step explanation:
Answer:
5.6
Step-by-step explanation:
Daphne has a preloaded games card that she is using to play games at the arcade as shown in the table.
How much did Daphne start with on her card?
by what amount does her card value change per game?
write an equation to represent the situation.

Answers
(a) Daphne starts with $25.00 on her card
(b) The amount by which her card value changes per game is -($0.5)
(c) y = 25 - 0.5·x
From the table of values, the amount
The table of values is presented as follows;
\(\begin{array}{ccc}&\ \ Games \ Played#&Amount \ on \ Card \ (\$)\\Start&0&25\\&3&23.5\\&6&22\\&9&20.50\end{array}\)
(a) From the table above, when the number of game played = 0, the amount on the card = 25
Therefore;
The amount that Daphne start with on her card = $25
(b) The amount her card changes per game is given by the rate of change as follows;
\(Rate \ of \ change = \dfrac{dy}{dx}\)
Therefore;
\(Rate \ of \ change = \dfrac{y_2 - y_1}{x_2 - x_1}\)
Which gives;\(Rate \ of \ change = \dfrac{Present \ amount \ on \ card - Previous \ amount \ on \ card}{Present \ number of games played - Previous\ number of games played}\)Taking any two points, we get;
Rate of change = (23.5 - 25)/(3 - 0) = -0.5
Therefore, her card value is drops by 0.5 per game
The amount by which her card value changes per game = -($0.5)
(c) We note that the rate of change of the Amount on Card, y, to the
number of Games Played, x, is constant, therefore, the relationship
between the variables is a straight line relationship, of the form, y = m·x + c, and we have;
m = The rate of change = -0.5
c = The y-intercept = The starting Amount on Card ($) = 25
Therefore, the equation is;
y = -0.5·x + 25 = 25 - 0.5·x
The required equation is, y = 25 - 0.5·x
Where;
y = The Amount on Card
x = The number of Games Played
Learn more about straight line equations here;
https://brainly.com/question/16934180
8. Write a paragraph proof.
Proof Given: In a plane, a is perpendicular to b, b id perpendicular to c, and c || d.
Prove: a || d
Answers
To prove that line segment a is parallel to line segment d, based on the given information, we can utilize the properties of perpendicular and parallel lines.
Given that a is perpendicular to b and b is perpendicular to c, we know that angles formed between a and b, as well as between b and c, are right angles. Let's denote these angles as ∠1 and ∠2, respectively.
Now, since c is parallel to d, we can conclude that the corresponding angles ∠2 and ∠3, formed between c and d, are congruent.Considering the fact that ∠2 is a right angle, it can be inferred that ∠3 is also a right angle.
By transitivity, if ∠1 is a right angle and ∠3 is a right angle, then ∠1 and ∠3 are congruent.Since corresponding angles are congruent, and ∠1 and ∠3 are congruent, we can deduce that line segment a is parallel to line segment d.
Thus, we have successfully proven that a is parallel to d based on the given information and the properties of perpendicular and parallel lines.
For more such questions on line segment
https://brainly.com/question/30756145
#SPJ8
What is the solution set for 3x−(x+2)≤4x−4 ? x≥1 x≤−2 x≤−6 x≥3
Answers
Answer:
x>1 (the first one)
Step-by-step explanation:
Pavel drew a triangle in his geometry notebook. The base of his triangle measured 10 centimeters.
Which of the following options could be the measures of the other two sides of his triangle?
A. 1 cm and 8 cm
B. 3 cm and 7 cm
c. 5 cm and 15 cm
D. 12 cm and 17 cm
Answers
The measure of other two sides of triangle is12cm and 17cm.
What is a triangle?
A polygon with three edges and three vertices is called a triangle. It is one of the fundamental geometric shapes.
In Euclidean geometry, any three points that are not collinear produce a singular triangle and a singular plane. In other words, every triangle is contained in a plane, and there is only one plane that contains that triangle.
If all of geometry is the Euclidean plane, then all triangles are enclosed in a single plane, however in higher-dimensional Euclidean spaces, this is no longer the case. Except when otherwise specified, this article discusses triangles in Euclidean geometry, namely the Euclidean plane.
here it is given in the question
the base of the triangle is 10cm.
then the value of other two side is 12cm and 17cm.
Hence, The measure of other two sides of triangle is12cm and 17cm.
To learn more about triangle refer to:
https://brainly.com/question/17335144
#SPJ1
This graph shows how the length of time a canoe is rented is related to the rental cost. What is the rate of change shown in the graph? Canoe Rental N Cost (9) g Time (hours) O A. $6/hour O B. 6 hours/dollar O c. $3/hour D. 3 hours/dollar

Answers
I'm pretty sure that the answer is A
What are the center and radius of the circle with equation (x − 1)² + (y + 4)² = 4? need answers right now
0 center (-1,4); r=2
0 center (-1, 4); r=4
0 center (1,-4); r=2
0 center (1,-4); r=4
Answers
Answer:
Option: C
Step-by-step explanation:
The center and radius of the circle with equation (x - 1)² + (y + 4)² = 4 are:
Center: (1, -4)
Radius: 2
So the correct answer is: Center (1, -4); r=2\(\)
A dog breeder would like to know how many Dalmatian puppies are typically born in a litter. He conducts some research and selects a random sample of 101 Dalmatian birth records. He examines each birth record and identifies the number of puppies that were born in the litter. The distribution of the number of puppies born per litter was skewed left with a mean of 6.2 puppies born per litter and a standard deviation of 2.1 puppies per litter. He would like to estimate, with 99% confidence, the mean number of puppies born per litter for all Dalmatian births. Which of the following is the correct interval?
a. 6.2 ± 2.576(0.21)
b. 6.2 ± 2.576(2.1)
c. 6.2 ± 2.626(0.21)
d. 6.2 ± 2.626(2.1)
e. The confidence interval
Answers
Answer:
c. 6.2 ± 2.626(0.21)
Step-by-step explanation:
We have the standard deviation for the sample, which means that the t-distribution is used to solve this question.
The first step to solve this problem is finding how many degrees of freedom, we have. This is the sample size subtracted by 1. So
df = 101 - 1 = 100
99% confidence interval
Now, we have to find a value of T, which is found looking at the t table, with 100 degrees of freedom(y-axis) and a confidence level of \(1 - \frac{1 - 0.99}{2} = 0.995\). So we have T = 2.626
The confidence interval is:
\(\overline{x} \pm M\)
In which \(\overline{x}\) is the sample mean while M is the margin of error.
The distribution of the number of puppies born per litter was skewed left with a mean of 6.2 puppies born per litter.
This means that \(\overline{x} = 6.2\)
The margin of error is:
\(M = T\frac{s}{\sqrt{n}} = 2.626\frac{2.1}{\sqrt{101}} = 2.626(0.21)\)
In which s is the standard deviation of the sample and n is the size of the sample.
Thus, the confidence interval is:
\(\overline{x} \pm M = 6.2 \pm 2.626(0.21)\)
And the correct answer is given by option c.
Given: a || b
Find the missing angle measures in the diagram. Explain how you find each angle measure. (please explain how you got the answer)

Answers
The angle measure explained in the solution.
Given that, a || b, we need to find the missing angles,
∠1 = 42° [vertically opposite angles]
∠3 = 62° [vertically opposite angles]
∠2 = 180°-(∠1+62°) [angle in a straight line]
∠2 = 76°
∠4 = ∠2 [vertically opposite angle]
∠4 = 76°
∠4 = ∠9 = 76° [alternate angles]
∠9 = ∠12 = 76° [vertically opposite angle]
∠3 = ∠ 6 = 62° [alternate angles]
∠ 6 = ∠7 = 62° [vertically opposite angle]
∠3 + ∠5 = 180° [consecutive angles]
∠5 = 118°
∠5 = ∠8 = 118° [vertically opposite angle]
∠4 + ∠10 = 180° [consecutive angles]
∠10 = 104°
∠10 = ∠11 [vertically opposite angle]
Learn more about angles, click;
https://brainly.com/question/28451077
#SPJ1
Calc question — related rates

Answers
The rate at which the depth of the liquid is increasing when the depth of the liquid reaches one-third of the height of the bowl is 1.25 cm s⁻¹.
How to determine rate?The volume of the liquid in the bowl is given by the following integral:
\(V = \int\limitsx_{0}^{h} \, \pi r^{2}(y) dy\)
where r = radius of the bowl and y = height of the liquid.
The radius of the bowl is equal to the distance from the curve y = (4/(8-x)) - 1 to the y-axis. This can be found using the following equation:
r = √{(4/(8-x)) - 1}² + 1²
The height of the liquid is equal to the distance from the curve y = (4/(8-x)) - 1 to the x-axis. This can be found using the following equation:
h = (4/(8-x)) - 1
Substituting these equations into the volume integral:
\(V = \int\limitsx_{0}^{h } \, \pi {\sqrt{(4/(8-x)) - 1)^{2} + 1^{2} (4/(8-x))} - 1 dy\)
Evaluate this integral using the following steps:
Expand the parentheses in the integrand.
Separate the integral into two parts, one for the integral of the square root term and one for the integral of the linear term.
Integrate each part separately.
The integral of the square root term can be evaluated using the following formula:
\(\int\limits^{b} _{a} \, dx \sqrt{x} dx = 2/3 (x^{3/2}) |^{b}_{a}\)
The integral of the linear term can be evaluated using the following formula:
\(\int\limits^{b} _{a} \, {x} dx = (x^{2/2}) |^{b}_{a}\)
Substituting these formulas into the integral:
V = π { 2/3 (4/(8-x))³ - 1/2 (4/(8-x))² } |_0^h
Evaluating this integral:
V = π { 16/27 (8-h)³ - 16/18 (8-h)² }
The rate of change of the volume of the liquid is given by:
dV/dt = π { 48/27 (8-h)² - 32/9 (8-h) }
The rate of change of the volume of the liquid is 7π cm³ s⁻¹. Also the depth of the liquid is one-third of the height of the bowl. This means that h = 2/3.
Substituting these values into the equation for dV/dt:
dV/dt = π { 48/27 (8-2/3)² - 32/9 (8-2/3) } = 7π
Solving this equation for the rate of change of the depth of the liquid:
dh/dt = 7/(48/27 (8 - 2/3)² - 32/9 (8 - 2/3)) = 1.25 cm s⁻¹
Therefore, the rate at which the depth of the liquid is increasing when the depth of the liquid reaches one-third of the height of the bowl is 1.25 cm s⁻¹.
Find out more on linear equations here: https://brainly.com/question/14323743
#SPJ1
identify each triangle right if it is an equilateral, isosceles or scalene triangle, or if it is an obtuse triangle, acute triangle, or right triangle opposite each letter below

Answers
Answer:
a) isosceles triangle / acute triangle
b) right angled triangle
c) isosceles triangle / acute triangle
d) right angled triangle
e) isosceles triangle / acute triangle
f) equilateral triangle
g) equilateral triangle
h) obtuse triangle
hope this answer helps you.....
Math Homework: Unit 3 Assignment
