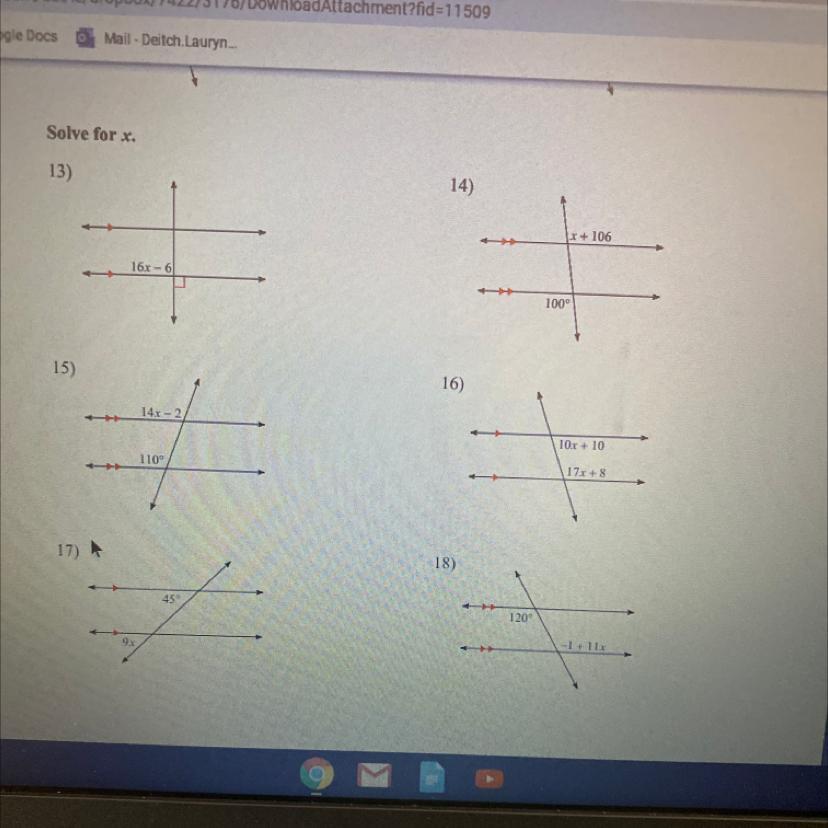
Answers
Answer:
x=?
Step-by-step explanation:
Related Questions
If You KNOW This I will mark Brainiest




Answers
Answer:
6a. x = 5/3
6b. x = 2
7a. x = 17
7b. y = 30, x = 3
8. 90-55 = 35
9. 180-30=150
10. 17 - 5 =12
11. opposite and corresponding angles (explanation beneath)
Step-by-step explanation:
6a. 7x-10=x+2
7x=x+10 (add 10 to both sides)
6x=10 (subtract x from both sides)
x = 5/3
6b. -3x+5(3x-1)=2x+15
12x-5=2x+15 (simplify the left side)
12x=2x+20 (add 5 to both sides)
10x=20 (subtract 2x from both sides)
x = 2
7a. (3x-10)+(2x+15) = 90
90+10= 100
100-15= 85
85/5 = 17 (as 3x + 2x = 5x)
x = 17
7b. 5y-45 = 3y +15
5y = 3y +60 (add 45 to both sides)
2y = 60 (subtract 3y from both sides)
y = 30
sub 30 for y into 3y+15: 90+15=105
straight line = 180
180-105=75
25x=75
75/25=3
x=3
8. complementary means 90º total
90-55=35 or 55+35 = 90
9. linear pair mean 180º total
180-30=150 or 30+150 =180
10. LF = 17
as LE is equal to FT, they both are equal to 5
as LE is part of LF, 17 - 5 =12
11. lm and rs are parallel
given that 9 and 12 are opposite angles, and that 12 and 8 are corresponding angles, meaning that 12 and 8 are of the same angle.
and since 12 = 8, and 12 = 9,
therefore you can prove that 8 = 9
Answer:
6. (a)
\(7x - 10 = x + 2\)
Collect like terms
\(7x - x = 2 + 10\)
\(6x = 12\)
Divide both sides with 6
\(x = \frac{12}{6} \)
\(x = 2\)
6. (b)
\( - 3x + 5(3x - 1) = 2x + 15\)
Expand the bracket\( - 3x + 15x - 5 = 2x + 15\)
Collect like terms
\( - 3x + 15x - 2x = 5 + 15\)
\( 10x = 20\)
Divide both sides with 10
\(x = \frac{20}{10} \)
\(x = 2\)
7.(a)
\((2x + 15) + (3x - 10) = 90\)
\(2x + 15 + 3x - 10 = 90\)
\(5x = 90 - 15 + 10\)
\(5x = 85\)
\(x = 17\)
7.(b)
(5y-45)° and (3y+15)° are opposite angles. Thus, they share the same value of angle.
\(5y - 45 = 3y + 15\)
\(5y - 3y = 45 + 15\)
\(2y = 60\)
\(y = 30\)
All four angles shown in the diagram will add up to a total value of 360°. So, minus 360° with the two angles we had found to find the remaining angles or x.
\(360 - (5(30) - 45) - (3(30) + 15) = 2(25x)\)
\(360 - 105 - 105 = 50x\)
\(150 = 50x\)
\(50x = 150\)
\(x = \frac{150}{50} \)
\(x = 3\)
SOMEONE PLZ HELP ME ASAP!!!!
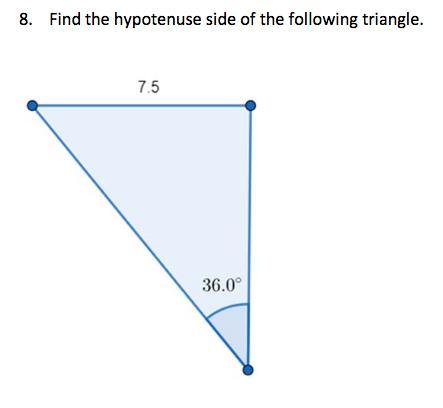
Answers
Answer:
hyp=12.76
Step-by-step explanation:
sin36=opp/hyp
hyp=opp/sin36
hyp=7.5/sin36
hyp=12.76 rounded to the nearest hundredth
To improve the safety of motorists, modern cars are built so that the front-end crumples upon impact. A 1200 kg car is travelling at a constant velocity of 8 m/s. It hits a wall and comes to a complete stop. If the wall exerts a force of 38000 N on the car, how long would it take the car to come to rest?
Answers
The required time that took the car to stop is 0.25 seconds.
Given that,
A 1200 kg car is traveling at a constant velocity of 8 m/s. It hits a wall and comes to a complete stop. If the wall exerts a force of 38000 N on the car, how long would it take the car to come to rest is to be determined.
Distance is defined as the object traveling at a particular speed in time from one point to another.
Here,
u = 8
V = 0
force = 38000
m = 1200
Calculating accelartion, by newton's second law,
force = ma
38000 = 1200a
a = 31.6,
Applying the first equation of motion,
v = u + at
0 = 8 + -31.6t [took negative because the acceleration is in opposite direction]
8/31.6 = t
t = 0.25
Thus, the required time that took the car to stop is 0.25 seconds.
Learn more about distance here:
brainly.com/question/15172156
#SPJ1
What percentage of the data values represented on a box plot falls between the lower quartile and the upper quartile?.
Answers
So, the percentage of data values represented on a box plot that falls between the lower quartile and the upper quartile is 50%.
In a box plot, the lower quartile (Q1) represents the 25th percentile, and the upper quartile (Q3) represents the 75th percentile. The interquartile range (IQR) is the range between the lower quartile and the upper quartile. To determine the percentage of data values that fall between the lower quartile and the upper quartile, we need to consider the IQR.
The IQR represents the middle 50% of the data. Therefore, the percentage of data values between the lower quartile and the upper quartile is 50%. In other words, half of the data values are within the IQR range, while the remaining 50% are outside this range, including the lower 25% below the lower quartile and the upper 25% above the upper quartile.
To know more about percentage,
https://brainly.com/question/14618268
#SPJ11
A Ioan is made for \( \$ 3500 \) with an interest rate of \( 9 \% \) and payments made annually for 4 years. What is the payment amount?
Answers
The payment amount for the loan is approximately $832.54.
To calculate the payment amount for a loan, we can use the formula for the present value of an annuity. The formula is as follows:
\[ P = \frac{A \times r}{1 - (1 + r)^{-n}} \]
Where:
- P is the loan principal (initial amount borrowed)
- A is the payment amount
- r is the interest rate per period (expressed as a decimal)
- n is the total number of periods
In this case, the loan principal (P) is $3500, the interest rate (r) is 9% (or 0.09 as a decimal), and the number of periods (n) is 4 (since payments are made annually for 4 years). We need to solve for A, the payment amount.
Plugging in the given values into the formula, we get:
\[ 3500 = \frac{A \times 0.09}{1 - (1 + 0.09)^{-4}} \]
To solve for A, we can rearrange the equation:
\[ A = \frac{3500 \times 0.09}{1 - (1 + 0.09)^{-4}} \]
Let's calculate the value of A using this equation:
\[ A = \frac{3500 \times 0.09}{1 - (1.09)^{-4}} \]
\[ A \approx \frac{315}{0.3781} \]
\[ A \approx \$832.54 \]
Learn more about loan repayment here:brainly.com/question/30281186
#SPJ11
solve the system4x - 2y + 3z = -32x - 4y + 2z = 16x + 10z = -2enter your answer as an ordered triple
Answers
Now, from equation (5)
\(\begin{gathered} x=10y+8 \\ x=10\times\frac{25}{28}+8 \\ x=16.92 \\ \text{Now, from the eqution(4)} \\ z=6y+5 \\ z=6\times\frac{25}{28}+5 \\ z=10.35 \end{gathered}\)Which expression is equivalent to \frac{r^9}{r^3}
Answers
Answer:
\(\sf r^6\)
Step-by-step explanation:
Exponent law:\(\boxed{\bf \dfrac{a^m}{a^n}=a^{m-n}}\)
In exponent division, if bases are same, subtract the powers.
\(\sf \dfrac{r^9}{r^3}=r^{9-3}=r^{6}\)
the within-groups estimate of variance is the estimate of the variance of the population of individuals based on the variation among the:
Group of answer choices
Scores in each of the actual groups studied
Mean of the groups minus the mean of the scores of the actual groups
Equal to the between-groups estimate of population variance
Means of the groups studied
Answers
The within-group estimate of variance is the estimate of the variance of the population of individuals based on the variation among the scores in each of the actual groups studied.
The within-groups estimate of variance is the estimate of the variance of the population of individuals based on the variation among the:
Scores in each of the actual groups studied.
This estimate represents the variation within each group and helps in understanding the population's variance by looking at individual differences within the groups.
The estimated within-group variance is the sum of the within-group variances for each group in the model. Effectively, this is the sum of the variance of each value (j) from its group (i) divided by the sample size minus one.
Learn more about Variance:
brainly.com/question/13708253
#SPJ11
Given secant of theta is equal to the square root of 10 over 2 comma what is cos?
a. one fifth
b. 5
c. square root of 10 over 2
d. square root of 10 over 5
Answers
Answer:
D square root of 10 over 5
Step-by-step explanation:
sec means \(\frac{1}{x}\), so if sec of theta is \(\frac{\sqrt{10} }{2}\) in this situation then you can set those equal to one another to get x.
x=\(\frac{\sqrt{10} }{5}\)
cos is just another way to say x so what you got for x is your answer
The secant of theta is equal to the square root of 10 over 2 comma what is, then the value of cos is square root of 10 over 5 .The correct option is d.
What is secant?For a right angle triangle, secant of the angle formed by the sides opposite to hypotenuse is equal to the ratio of Hypotenuse and the base of triangle,
Given the value of sec of θ
secθ = sqrt (10)/2
Then cos θ = 1/secθ
Plug the value, we get
secθ= sqrt (10) / 5
Thus, the correct option is d.
Learn more about secant.
https://brainly.com/question/23026602
#SPJ1
f(x) = (x-2)(x+1)
————-
x+1
Which statements describe the end behavior of the graph of the function shown? Check all that apply.
• As x to infinity, y to 1.
•As x to infinity, y to infinity
•As x to infinity, y to negative infinity
•As x to negative infinity, y to - 1
•As x to negative infinity, y to infinity
•As x to negative infinity, y to negative infinity
Answers
Answer:
As x to negative infinity, y to negative infinity
Step-by-step explanation:
refer to the function f= (7,2), (9,7), (4,9), (3,4)
Determine f(7)
f(7)=?
Answers
Since we are looking for the value of f(7), we need to find the corresponding output value when the input is 7. From the given function, we see that input 7 corresponds to output 2. f(7) = 2.
To determine the value of f(7), we need to look at the given function f and substitute 7 for the independent variable.
The function f is defined by the ordered pairs (7,2), (9,7), (4,9), and (3,4). The first value in each ordered pair represents the input, while the second value represents the output.
In summary, when we substitute 7 for the independent variable in the given function f = (7,2), (9,7), (4,9), (3,4), we find that f(7) = 2.
For more such questions on output value
https://brainly.com/question/20956194
#SPJ8
Amelie is shopping for children's books and puzzle books. She wants to purchase at least 2 more children's books than puzzle books, but she can afford no more than 15 items total. If x represents the number of children's books and y represents the number of puzzle books Amelie purchases, which point lies in the solution set?
Answers
Answer:
X = 8.5, Y = 6.5
Step-by-step explanation:
X = # of children's books
Y = # of puzzle books
Amelie wants to buy 2 more children's books than puzzle books.
15 - 2 = 13 (Save the 2)
13 / 2 = 6.5
6.5 + 2 = 8.5
So; 8.5 + 6.5 = 15
X = 8.5
Y = 6.5
6 16 Next → Pretest: Scientific Notation Drag the tiles to the correct boxes to complete the pairs.. Particle Mass (grams) proton 1.6726 × 10-24 The table gives the masses of the three fundamental particles of an atom. Match each combination of particles with its total mass. Round E factors to four decimal places. 10-24 neutron 1.6749 × electron 9.108 × 10-28 two protons and one neutron one electron, one proton, and one neutron Mass 0-24 grams two electrons and one proton one proton and two neutrons Submit Test Particles F
Answers
We can drag the particles in mass/grams measurement to the corresponding descriptions as follows:
1. 1.6744 × 10⁻²⁴: Two electrons and 0ne proton
2. 5.021 × 10⁻²⁴: Two protons and one neutron
3. 5.0224 × 10⁻²⁴: One proton and two neutrons
4. 3.3484 × 10⁻²⁴: One electron, one proton, and one neutron
How to match the particlesTo match the measurements to the descriptions first note that one neutron is 1.6749 × 10⁻²⁴. One proton is equal to 1.6726 × 10⁻²⁴ and one electron is equal to 9.108 × 10⁻²⁸.
To obtain the right combinations, we have to add up the particles to arrive at the constituents. So, for the figure;
1.6744 × 10⁻²⁴, we would
Add 2 electrons and one proton
= 2(9.108 × 10⁻²⁸) + 1.6726 × 10⁻²⁴
= 1.6744 × 10⁻²⁴
The same applies to the other combinations.
Learn more about electrons and protons here:
https://brainly.com/question/1481324
#SPJ1
The sum of the measures of the interior angles of a
convex quadrilateral is
a. 180°
b. 270°
c. 540°
d. 360°
Answers
Answer:
d. 360°
Hope this help!
4x-2y+3z= 23
X+ 5y - 3z -37
- 2x+y+4z = 27
Answers
Answer:
solving for x - 23/4 + 1/2y -3/4z
Step-by-step explanation:
Pls help and show workings
6-4-5-6-2+6
Answers
Answer:
−5
Step-by-step explanation:
6−4−5−6−2+6
Subtract 4 from 6 to get 2.
2−5−6−2+6
Subtract 5 from 2 to get −3.
−3−6−2+6
Subtract 6 from −3 to get −9.
−9−2+6
Subtract 2 from −9 to get −11.
−11+6
Add −11 and 6 to get −5.
−5
Answer:
-5
Step-by-step explanation:
6 - 4 = 2
2 - 5 = -3
-3 - 6 = -9
-9 - 2 = -11
-11 + 6 = -5
A bag contains 2 green marbles and 5 red marbles. Two marbles are drawn at random as follows; one marble is drawn and not replaced. then the second marble is drawn.
What is the probability that the first marble is red and the second one is green
Answers
Answer:
.8
Step-by-step explanation:
Which expressions are equivalent to the one below? Check all that apply.
log 2-log 6
A. log 3
B. log 2
C. log(2) + log
-log()
□ D. log()
Answers
Equivalent expression for the expression ( log 2 - log 6 ) is,
⇒ - log 3
What is an expression?Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
The expression is,
⇒ log 2 - log 6
Now, Simplify the expression by using logarithmic rule as;
⇒ log 2 - log 6
⇒ log 2 / 6
⇒ log 1/3
⇒ log 3⁻¹
⇒ - log 3
Therefore, We get;
Equivalent expression for the expression ( log 2 - log 6 ) is,
⇒ - log 3
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ9
The curve y tan x crosses the line y = 7x at a non-zero x-value between x = 0 and X Ξ . Use Newton's method to find where the curves intersect. The curve y = tan x crosses the line y = 7x at x = (Type an integer or decimal rounded to seven decimal places as needed.) Enter your answer in the answer box. 8:04 PM O Type here to search
Previous question
Next
Answers
To find the intersection point between the curve y = tan(x) and the line y = 7x, we can use Newton's method. Newton's method is an iterative numerical method used to approximate the root of a function.
We need to find the x-value where the curves intersect, so we can set up the equation tan(x) - 7x = 0. We want to find a solution between x = 0 and some unknown value denoted as X.
Using Newton's method, we start with an initial guess x_0 for the solution and iterate using the formula:
x_(n+1) = x_n - f(x_n) / f'(x_n),
where f(x) = tan(x) - 7x and f'(x) is the derivative of f(x).
We continue this iteration until we reach a desired level of accuracy or convergence. The resulting value of x will be the approximate intersection point between the two curves.
Please note that without specific values or range for X or an initial guess x_0, it is not possible to provide a specific numerical answer. However, you can apply Newton's method using an initial guess and the given function to find the approximate intersection point.
Learn more about Newton's method here:
https://brainly.com/question/31910767
#SPJ11
The product of 2 consecutive positive odd integers is 483. Write the equation that would be used to find x, the smaller integer.
Answers
Answer: 21
Step-by-step explanation:
Let the consecutive odd numbers be represented by x and x+2. Therefore,
x × (x+2) = 483
x² + 2x = 483
x² + 2x - 483 = 0
x² + 23x - 21x - 483 = 0
x(x + 23) - 21(x + 23) = 0
(x - 21) = 0
x = 0 + 21
x = 21
The smaller integer is 21
The larger integer is 21 + 2 = 23.
Find the general solution to the homogeneous system of DE: -11 x' = Ax where A = [-26 41 Hint: Write your answer x(t) in the form of eat [cos(ht) + sin(bt)].
Answers
The general solution to the homogeneous system of differential equations is:
x(t) = c₁ * \(e^{(-7t)\) * | 4 | + c₂ * \(e^{(-20t)\) * | 2 |
|-1 |
where c₁ and c₂ are constants.
To find the general solution to the homogeneous system of differential equations -11x' = Ax, where A = [-26 4; 1 1], we first need to find the eigenvalues and eigenvectors of matrix A.
To find the eigenvalues, we solve the characteristic equation:
det(A - λI) = 0
Substituting the values, we get:
| -26-λ 4 |
| 1 1-λ |
Expanding the determinant, we have:
(-26-λ)(1-λ) - 4 = 0
Simplifying and solving the equation, we find the eigenvalues:
λ₁ = -7
λ₂ = -20
Next, let's find the corresponding eigenvectors.
For λ₁ = -7:
(A + 7I)v₁ = 0
| -19 4 |
| 1 8 |
Solving the system of equations, we find the eigenvector corresponding to λ₁:
v₁ = | 4 |
|-1 |
For λ₂ = -20:
(A + 20I)v₂ = 0
| -6 4 |
| 1 21 |
Solving the system of equations, we find the eigenvector corresponding to λ₂:
v₂ = | 2 |
|-1 |
Now that we have the eigenvalues and eigenvectors, we can write the general solution to the system of differential equations as:
Substituting the values of the eigenvalues and eigenvectors, we get:
x(t) = c₁ * \(e^{(-7t)\) * | 4 | + c₂ * \(e^{(-20t)\) * | 2 |
|-1 |
Simplifying this expression, we get:
x(t) = | 4c₁ * \(e^{(-7t)\) + 2c₂ * \(e^{(-20t)\) |
|-c₁ * \(e^{(-7t)\) - c₂ * \(e^{(-20t)\)) |
Therefore, the general solution to the homogeneous system of differential equations is:
x(t) = c₁ * \(e^{(-7t)\) * | 4 | + c₂ * \(e^{(-20t)\) * | 2 |
|-1 |
where c₁ and c₂ are constants.
Learn more about Homogeneous System at
brainly.com/question/30502489
#SPJ4
Given the following exponential function, identify whether the change represents
growth or decay, and determine the percentage rate of increase or decrease.
y = 61(0.95)*
Answers
In the exponential function y = 61 (0.95)^t, the change represents a decay.
The percentage of decay rate is 5%.
What is an exponential function?
The formula for an exponential function is f(x) = a^x, where x is a variable and a is a constant that serves as the function's base and must be bigger than 0.
The given exponential function is -
y = 61 (0.95)^t
Here, it can be seen that there is a decay rate as the base value 0.95<1.
The percentage rate of decrease is 1-0.95.
Find the percentage decay rate as -
= 1 - 0.95
= 0.05
Convert it into percentage -
= 0.05 × 100
= 5 %
Therefore, the exponential function is a decay function with 5% decay rate.
To learn more about exponential function from the given link
brainly.com/question/30241796
#SPJ1
in 250 explain the power of substitutes from porters 5
forces
Answers
The power of substitutes is one of the five forces in Porter's Five Forces framework and it is a measure of how easy it is for customers to switch to alternative products or services. The higher the power of substitutes, the more competitive the industry and the lower the profitability.
The power of substitutes is based on the premise that when there are readily available alternatives to a product or service, customers can easily switch to those alternatives if they offer better value or meet their needs more effectively. This poses a threat to the industry as it reduces customer loyalty and puts pressure on pricing and differentiation strategies.
The availability and quality of substitutes influence the degree to which customers are likely to switch. If substitutes are abundant and offer comparable or superior features, the power of substitutes is strong, increasing the competitive intensity within the industry. On the other hand, if substitutes are limited or inferior, the power of substitutes is weak, providing more stability and protection to the industry.
To know more about Porter's Five Forces framework here: brainly.com/question/32990982
#SPJ11
The volume of a sphere is 26667 cm³.
Calculate the diameter of the sphere.
Volume of sphere = πr³
cm

Answers
Given the volume of the sphere as 26667 cm³, we calculated the radius to be approximately 17.7 cm using the formula for the volume of a sphere. By multiplying the radius by 2, we found that the diameter of the sphere is approximately 35.4 cm.
To calculate the diameter of a sphere when given its volume, we can use the formula for the volume of a sphere:
V = (4/3) * π * r³
Where V is the volume and r is the radius of the sphere. Since we are given the volume, we can rearrange the formula to solve for the radius:
r = (\(\sqrt[3]{(3V / (4\pi )}\)))
Substituting the given volume V = 26667 cm³ into the formula, we have:
r = (\(\sqrt[3]{(3 * 26667 / (4\pi )))}\)
Calculating this expression, we find:
r ≈ (\(\sqrt[3]{80001 / \pi ))}\) ≈ 17.7 cm
Now that we have the radius, we can calculate the diameter by multiplying the radius by 2:
d = 2 * r ≈ 2 * 17.7 ≈ 35.4 cm
For more such information on: volume
https://brainly.com/question/463363
#SPJ8
(3) The difference between two numbers is 8. If the larger is
subtracted from three times the smaller, the difference is 100. Find
the numbers.
Answers
Answer:
x= 62
y= 54
Step-by-step explanation:
Step one:
given data
let the numbers be x and y and the larger be x the smaller be y
The difference between two numbers is 8
x-y= 8-----------1
If the larger is subtracted from three times the smaller, the difference is 100
3y-x=100------------2
from eqn 1, x= 8+y
put this in eqn 2
3y-(8+y)=100
3y-8-y=100
collect liker terms
3y-y-8=100
2y=108
y= 54
put y= 54 in eqn 1
x-y=8
x-54= 8
x= 8+54
x=62
Pls help ASAP will mark Brainlyest!!
Find the area of the following figure.
1. 312 cm2
2. 400 cm2
3. 252 cm2
4. 300 cm2

Answers
Answer:
312cm2
Step-by-step explanation:
Area of the triangles:
A =1/2bh
A=1/2(10*12) = 1/2*120=60.
There are two triangles. 60*2=120. 120 is the area of both triangles.
Area of the rectangle:
16*12=192.
120+192=312cm2
Explanation: I had this question before I got 100. Please give Brainlyest
Find the values of x for which the series converges. (Give the answer using interval notation.)
∑[infinity]n=0x−5n9n
Answers
The given series ∑[infinity]n=0x−5n9n converges for all x in the interval (-4,14) in the real number system.
To determine the convergence of the given series, we can use the ratio test. Applying the ratio test, we get:
|((x-5(n+1))/9(n+1)) / ((x-5n)/9n)| = |(x-5)/(9(n+1))|.
For the series to converge, we need the limit of the ratio as n approaches infinity to be less than 1 in absolute value. Hence, we have:
lim(n→∞) |(x-5)/(9(n+1))| < 1
|x-5|/9 < 1
|x-5| < 9
This implies -4 < x-5 < 14, or -4 < x < 14. Therefore, the given series converges for all x in the interval (-4,14) in the real number system.
Learn more about interval here:
https://brainly.com/question/29126055
#SPJ11
A=P(1+r/n)^nt Find how long it takes for $1400 to double if it is invested at 7% interest compounded monthly. Use the formula A = P to solve the compound interest problem. TE The money will double in value in approximately years. (Do not round until the final answer. Then round to the nearest tenth as needed.)
Answers
It will take 10 years to double the amount.
Given that, the amount $1400 to double if it is invested at 7% interest compounded monthly, we need to calculate the time,
\(A = P(1+r/n)^{nt}\)
\(2800 = 1400(1+0.0058)^{12t}\)
\(2= (1.0058)^{12t\)
㏒ 2 = 12t ㏒ (1.0058)
0.03 = 12t (0.0025)
12t = 120
t = 10
Hence, it will take 10 years to double the amount.
Learn more about compound interest click;
https://brainly.com/question/14295570
#SPJ1
You deposit $100 in an investment account that earns 3% annual interest compounded monthly.
a. Write a function m that represents the balance (in dollars) of the investment account after t years.
m(t)=

Answers
B. m(5)=100(1.03)^5
m(5)=115.9 or 116 rounded up
Will has 35 buttons. He puts 5 buttons on his backpack. How many
buttons does Will have left?
Answers
Answer: 30 buttons
35 - 5 = 30
Answer:
30
35-5=30
Step-by-step explanation: