Answers
Answer:
Pythagorean theorem: a^2 + b^2 = c^2, a and b are the sides, c is the hypotenuse (longest side).
27^2 + 25^2 = x^2
Solving for x, we see that it is approximately 36.8.
Let me know if this helps!
Related Questions
a recent survey found that of all adults over wear glasses for driving. in a random sample of adults over , what is the probability that at least six wear glasses?
Answers
Let p be the probability of an adult over 50 wearing glasses for driving. Since we don't know the value of p, we can't use the binomial distribution directly. However, we can use the normal approximation to the binomial distribution since n is large (assuming n * p >= 10 and n * (1-p) >= 10).
Let X be the number of adults over 50 wearing glasses for driving in a random sample of n adults. Then X ~ Binomial(n, p) can be approximated by a normal distribution with mean µ = n * p and standard deviation σ = sqrt(n * p * (1-p)).
We want to find the probability that at least six adults over 50 in a random sample of n wear glasses for driving. This is equivalent to finding P(X >= 6) = 1 - P(X < 6) using the normal approximation.
To apply the normal approximation, we need to standardize the random variable X:
Z = (X - µ) / σ
Using continuity correction:
P(X >= 6) = P(X > 5.5)
Z = (5.5 - n * p) / sqrt(n * p * (1-p))
We can use the standard normal distribution table or calculator to find the probability:
P(Z >= (5.5 - n * p) / sqrt(n * p * (1-p)))
Since we don't know the value of p, we can use a conservative estimate of p = 0.5 (assuming 50% of adults over 50 wear glasses for driving). Then:
P(Z >= (5.5 - n * 0.5) / sqrt(n * 0.5 * (1-0.5)))
For example, if we sample n = 100 adults over 50, the probability of at least six wearing glasses is:
P(Z >= (5.5 - 100 * 0.5) / sqrt(100 * 0.5 * (1-0.5)))
= P(Z >= 0.5)
Using a standard normal distribution table or calculator, P(Z >= 0.5) = 0.3085.
Therefore, the probability of at least six adults over 50 wearing glasses for driving in a random sample of 100 is approximately 0.3085 or 30.85%.
For more details probability click here:
https://brainly.com/question/30034780#
#SPJ11
Are the two triangles congruent ? Please answer correctly !!!!!!!!!!!!! Will mark Brianliest !!!!!!!!!!!!!!!

Answers
Answer
YES
Step by step Explanation
Answer:
There is not information given to assume the triangles are congruent.
Step-by-step explanation:
You can tell if two triangles are congruent by any of the following rules:
Three sides are congruent (SSS),
Two angles and a side in between are congruent (ASA)
Two sides and an angle in between are congruent (SAS)
Two angles and a side connected to one of those angles are congruent (AAS)
Note: SSA (Two Sides & One Angle) does not work. I good way to remember is that it spells a bad word backwards :)
In this case, there are only two sides given, but there aren't any angles, so there is not enough information to conclude if they are congruent or not.
Suppose that a, b, c, d are positive real numbers such that a/b < c/d . What can you say about the fraction (a+c)/(b+d) ? Is it always, sometimes, or never between the fractions a/b and c/d ? Provide evidence of your claim. (If always or never, give an algebraic proof, otherwise, give two quadruples values of a, b, c, d in which one quadruple has (a+c)/(b+d) between a/b and c/d and the other does not.)
Answers
Answer: (a−c)(b−c)>0
Step-by-step explanation:
ab>1 and ac<01. a>0 if c<0 and also b>02. a<0 if c>0 and also b<0
how i did it:
At the vert first, write the inequality as an equation.
Solve the provided equation for one or more values.
Now, display all the values obtained in the number line.
Use open circles to show the excluded values on the number line.
Find the interim.
At the moment, take any random value from the interval and substitute it in the inequality equation to check whether the values reassure the inequality equation.
Intervals that reassure the inequality equation are the solutions of the given inequality equation.
At the city museum, child admission is $6.20 and adult admission is $9.40. On Thursday, 163 tickets were sold for a total sales of $1221.80. How many adult
tickets were sold that day?
Answers
To form a system of equation from a word problem, we must recognize different variables to form different equations.
Solving the QuestionLet a represent the number of child tickets.
Let b represent the number of adult tickets.
We're given:
1a = $6.201b = $9.40a and b in total is 163Total sales = $1221.80Because we're given that a and b in total is 163, we can form the following equation:
\(a+b=163\)
We're also given that the total sales made is $1221.80. Because we know that 1a = $6.20 and 1b = $9.40, we can also form the following equation:
\(6.2a+9.4b=1221.8\)
Here are our two equations:
\(a+b=163\)
\(6.2a+9.4b=1221.8\)
Solving the System of EquationsWe can solve using the method of elimination. Multiply both sides by 6.2 in the first equation:
\(6.2(a+b)=6.2(163)\\6.2a+6.2b=1010.6\)
Subtract this new equation from the second equation to cancel out a:
\(\hspace{10}6.2a+9.4b=1221.8\\- 6.2a+6.2b=1010.6\\\rule{100}{0.5}\\3.2b=211.2\)
Solve for b:
\(b=66\)
Therefore, the number of adult tickets sold is 66.
Answer66
Solve for y.
23 +18y=-21 + 14y
Simplify your answer as much as possible.
y =
Answers
Answer:
y = -11
Step-by-step explanation:
23 + 18y = -21 + 14y
Combine like terms
18y - 14y = -21 -23
Do the math
4y = -44
Divide both sides by 4
y = -11
There plz help me is my last question and assignment

Answers
Answer:
I believe Jamal is correct, because he is just doing it an easy way. Instead of converting the mixed number to an improper fraction he is adding the measurements step by step.
Hope it Helps!
:)
Can someone please help me with these 7 questions please?

Answers
The solution to each of the question takes different approach, as the questions are taken from different concepts; however, a common operation among all questions, is factorization.
\((1)\ (-xy)^3(xz)\)
Expand
\((-xy)^3(xz) = (-x)^3* y^3*(xz)\)
\((-xy)^3(xz) = -x^3* y^3*xz\)
Rewrite as:
\((-xy)^3(xz) = -x^3*x* y^3*z\)
Apply law of indices
\((-xy)^3(xz) = -x^4y^3z\)
\((2)\ (\frac{1}{3}mn^{-4})^2\)
Expand
\((\frac{1}{3}mn^{-4})^2 =(\frac{1}{3})^2m^2n^{-4*2}\)
\((\frac{1}{3}mn^{-4})^2 =\frac{1}{9}m^2n^{-8\)
\((3)\ (\frac{1}{5x^4})^{-2}\)
Apply negative power rule of indices
\((\frac{1}{5x^4})^{-2}= (5x^4)^2\)
Expand
\((\frac{1}{5x^4})^{-2}= 5^2x^{4*2}\)
\((\frac{1}{5x^4})^{-2}= 25x^{8\)
\((4)\ -x(2x^2 - 4x) - 6x^2\)
Expand
\(-x(2x^2 - 4x) - 6x^2 = -2x^3 + 4x^2 - 6x^2\)
Evaluate like terms
\(-x(2x^2 - 4x) - 6x^2 = -2x^3 -2x^2\)
Factor out x^2
\(-x(2x^2 - 4x) - 6x^2 = (-2x-2)x^2\)
Factor out -2
\(-x(2x^2 - 4x) - 6x^2 = -2(x+1)x^2\)
\((5)\ \sqrt{\frac{4y}{3y^2}}\)
Divide by y
\(\sqrt{\frac{4y}{3y^2}} = \sqrt{\frac{4}{3y}}\)
Split
\(\sqrt{\frac{4y}{3y^2}} = \frac{\sqrt{4}}{\sqrt{3y}}\)
\(\sqrt{\frac{4y}{3y^2}} = \frac{2}{\sqrt{3y}}\)
Rationalize
\(\sqrt{\frac{4y}{3y^2}} = \frac{2}{\sqrt{3y}} * \frac{\sqrt{3y}}{\sqrt{3y}}\)
\(\sqrt{\frac{4y}{3y^2}} = \frac{2\sqrt{3y}}{3y}\)
\((6)\ \frac{8}{3 + \sqrt 3}\)
Rationalize
\(\frac{8}{3 + \sqrt 3} = \frac{3 - \sqrt 3}{3 - \sqrt 3}\)
\(\frac{8}{3 + \sqrt 3} = \frac{8(3 - \sqrt 3)}{(3 + \sqrt 3)(3 - \sqrt 3)}\)
Apply difference of two squares to the denominator
\(\frac{8}{3 + \sqrt 3} = \frac{8(3 - \sqrt 3)}{3^2 - (\sqrt 3)^2}\)
\(\frac{8}{3 + \sqrt 3} = \frac{8(3 - \sqrt 3)}{9 - 3}\)
\(\frac{8}{3 + \sqrt 3} = \frac{8(3 - \sqrt 3)}{6}\)
Simplify
\(\frac{8}{3 + \sqrt 3} = \frac{4(3 - \sqrt 3)}{3}\)
\((7)\ \sqrt{40} - \sqrt{10} + \sqrt{90}\)
Expand
\(\sqrt{40} - \sqrt{10} + \sqrt{90} =\sqrt{4*10} - \sqrt{10} + \sqrt{9*10}\)
Split
\(\sqrt{40} - \sqrt{10} + \sqrt{90} =\sqrt{4}*\sqrt{10} - \sqrt{10} + \sqrt{9}*\sqrt{10}\)
Evaluate all roots
\(\sqrt{40} - \sqrt{10} + \sqrt{90} =2*\sqrt{10} - \sqrt{10} + 3*\sqrt{10}\)
\(\sqrt{40} - \sqrt{10} + \sqrt{90} =2\sqrt{10} - \sqrt{10} + 3\sqrt{10}\)
\(\sqrt{40} - \sqrt{10} + \sqrt{90} =4\sqrt{10}\)
\((8)\ \frac{r^2 + r - 6}{r^2 + 4r -12}\)
Expand
\(\frac{r^2 + r - 6}{r^2 + 4r -12}=\frac{r^2 + 3r-2r - 6}{r^2 + 6r-2r -12}\)
Factorize each
\(\frac{r^2 + r - 6}{r^2 + 4r -12}=\frac{r(r + 3)-2(r + 3)}{r(r + 6)-2(r +6)}\)
Factor out (r+3) in the numerator and (r + 6) in the denominator
\(\frac{r^2 + r - 6}{r^2 + 4r -12}=\frac{(r -2)(r + 3)}{(r - 2)(r +6)}\)
Cancel out r - 2
\(\frac{r^2 + r - 6}{r^2 + 4r -12}=\frac{r + 3}{r +6}\)
\((9)\ \frac{4x + 8}{x^2} \cdot \frac{x}{x^2 - 5x - 14}\)
Cancel out x
\(\frac{4x + 8}{x^2} \cdot \frac{x}{x^2 - 5x - 14} = \frac{4x + 8}{x} \cdot \frac{1}{x^2 - 5x - 14}\)
Expand the numerator of the 2nd fraction
\(\frac{4x + 8}{x^2} \cdot \frac{x}{x^2 - 5x - 14} = \frac{4x + 8}{x} \cdot \frac{1}{x^2 - 7x+2x - 14}\)
Factorize
\(\frac{4x + 8}{x^2} \cdot \frac{x}{x^2 - 5x - 14} = \frac{4x + 8}{x} \cdot \frac{1}{x(x - 7)+2(x - 7)}\)
Factor out x - 7
\(\frac{4x + 8}{x^2} \cdot \frac{x}{x^2 - 5x - 14} = \frac{4x + 8}{x} \cdot \frac{1}{(x + 2)(x - 7)}\)
Factor out 4 from 4x + 8
\(\frac{4x + 8}{x^2} \cdot \frac{x}{x^2 - 5x - 14} = \frac{4(x + 2)}{x} \cdot \frac{1}{(x + 2)(x - 7)}\)
Cancel out x + 2
\(\frac{4x + 8}{x^2} \cdot \frac{x}{x^2 - 5x - 14} = \frac{4}{x} \cdot \frac{1}{(x - 7)}\)
\(\frac{4x + 8}{x^2} \cdot \frac{x}{x^2 - 5x - 14} = \frac{4}{x(x - 7)}\)
\((10)\ (3x^3 + 15x^2 -21x) \div 3x\)
Factorize
\((3x^3 + 15x^2 -21x) \div 3x = 3x(x^2 + 5x -7) \div 3x\)
Cancel out 3x
\((3x^3 + 15x^2 -21x) \div 3x = x^2 + 5x -7\)
\((11)\ \frac{m}{6m + 6} - \frac{1}{m+1}\)
Take LCM
\(\frac{m}{6m + 6} - \frac{1}{m+1} = \frac{m(m + 1) - 1(6m + 6)}{(6m + 6)(m + 1)}\)
Expand
\(\frac{m}{6m + 6} - \frac{1}{m+1} = \frac{m^2 + m- 6m - 6}{(6m + 6)(m + 1)}\)
\(\frac{m}{6m + 6} - \frac{1}{m+1} = \frac{m^2 - 5m - 6}{(6m + 6)(m + 1)}\)
\((12)\ \frac{\frac{1}{y - 3}}{\frac{2}{y^2 - 9}}\)
Rewrite as:
\(\frac{\frac{1}{y - 3}}{\frac{2}{y^2 - 9}} = \frac{1}{y - 3} \div \frac{2}{y^2 - 9}\)
Express as multiplication
\(\frac{\frac{1}{y - 3}}{\frac{2}{y^2 - 9}} = \frac{1}{y - 3} * \frac{y^2 - 9}{2}\)
Express y^2 - 9 as y^2 - 3^2
\(\frac{\frac{1}{y - 3}}{\frac{2}{y^2 - 9}} = \frac{1}{y - 3} * \frac{y^2 - 3^2}{2}\)
Express as difference of two squares
\(\frac{\frac{1}{y - 3}}{\frac{2}{y^2 - 9}} = \frac{1}{y - 3} * \frac{(y - 3)(y+3)}{2}\)
\(\frac{\frac{1}{y - 3}}{\frac{2}{y^2 - 9}} = \frac{1}{1} * \frac{(y+3)}{2}\)
\(\frac{\frac{1}{y - 3}}{\frac{2}{y^2 - 9}} = \frac{y+3}{2}\)
Read more at:
https://brainly.com/question/4372544
Tomorrow, Mrs. Wendel's class will be using toothpicks for a science project. Each student must use at least 6 toothpicks for the project.
Mrs. Wendel knows that there is already a bag of 50 toothpicks in the class storage room. She plans to buy x additional toothpicks this afternoon to make sure her class will have enough.
If her class has 28 students, which number sentence represents this situation?
Answers
The table represents the cost of flowers at the Tigerlily Flower Shop.
Cost of Flowers
Quantity
Price
1
$2.00
2
$3.50
3
$5.00
4
$6.50
5
$8.00
6
$9.00
Which graph is the best interpretation of this table?
On a coordinate plane, the x-axis is labeled Quantity and the y-axis is labeled price. Points are at (1, 2), (2, 3.5), (3, 5), (4, 6.5), (5, 8), (6, 9).
On a coordinate plane, the x-axis is labeled Quantity and the y-axis is labeled price. Points are at (1, 2), (2, 4), (3, 6), (4, 8), (5, 10), (6, 12).
On a coordinate plane, the x-axis is labeled Quantity and the y-axis is labeled price. A line with positive slope goes through points (2, 4) and (4, 8).
On a coordinate plane, the x-axis is labeled Quantity and the y-axis is labeled price. A curved line with positive slope is on the graph.
Answers
The graph which is the best interpretation of the table given is; On a coordinate plane, the x-axis is labeled Quantity and the y-axis is labeled price. Points are at (1, 2), (2, 3.5), (3, 5), (4, 6.5), (5, 8), (6, 9).
Which graph is the best interpretation of the table?The table given in the task content is a tabular representation of the quantity and the corresponding prices. On this note, plotting the quantity on the x-axis and the price on the y-intercept with the point descriptions above best represents the graph of the table.
Read more on graph interpretation;
https://brainly.com/question/1638242
#SPJ1
Answer:
The short answer to my well taught friend, is A
help me yall pleasee :(

Answers
Answer:
line 2 has a mistake, you are supposed to add 6x to both sides and instead they subtracted
(-5, -4) and (-13,2)
Answers
The slope of the line passing through the points (-5, -4) and (-13, 2) is -3/4.
What is the slope of the line through the given points?Slope is simply expressed as a change in y over the change in x.
It is expressed as
\(m = \frac{y_2 - y_1}{x_2 - x_1}\)
Given the points:
(-5, -4) and (-13,2)
Point (-5, -4):
x₁ = -5
y₁ = -4
Point (-13,2):
x₂ = -13
y₂ = 2
Plug the given x and y values into the slope formula and simplify.
\(m = \frac{y_2 - y_1}{x_2 - x_1}\\\\m = \frac{2 - (-4)}{-13 - (-5)}\\\\m = \frac{2 + 4}{-13 + 5}\\\\m = \frac{6}{-8}\\\\m = -\frac{3}{4}\)
Therefore, the slope of the line is -3/4.
Learn more about slope formula here: brainly.com/question/24578307
#SPJ1
Still on a quest to determine a mathematical relationship between these two quantities, you collect a set of data points as follows.
points : -8, -6, -2, 8, 16
percentage points : 9, -9, -18, -63, -99
where
denotes the previous day's change in the Dow Jones, measured in points; and
denotes the net approval rating for the president of the United States, measured in percentage points.
Four of these five data points exactly fit a linear model =()
.
By computing slopes, determine which of the five points is not a perfect fit, and explain your answer.
Remove the point you found in part (a). Then, find a slope-intercept equation for the linear model =+
that passes through the remaining four data points.
In one "when-then" sentence, explain the practical meaning of the
-intercept of your linear model.
(How should we understand the meaning of that number, in terms of previous day's change in the Dow Jones and/or net approval rating for the president of the United States? Include units in your explanation as appropriate.)
In one sentence, explain the practical meaning of the slope of your linear model.
(How should we understand the meaning of that number, in terms of previous day's change in the Dow Jones and/or net approval rating for the president of the United States? Include units in your explanation as appropriate.)
Answers
The point (16, -99) is not a perfect fit in the linear model, and the slope-intercept equation for the remaining four data points (-8, 9), (-6, -9), (-2, -18), and (8, -63) is y = (-15/2)x + 3; the y-intercept (3) represents the net approval rating for the president when there is no change in the Dow Jones, and the slope (-15/2) indicates that for every 1-point increase in the Dow Jones, the net approval rating is expected to decrease by 7.5 percentage points.
To determine which point is not a perfect fit in the linear model, we need to compute the slopes for each pair of consecutive data points.
The slope of a linear model represents the rate of change between the two variables.
Using the given data points:
Points: -8, -6, -2, 8, 16
Percentage Points: 9, -9, -18, -63, -99
Let's compute the slopes:
Slope between (-8, 9) and (-6, -9):
slope = (change in percentage points) / (change in points)
slope = (-9 - 9) / (-6 - (-8))
slope = -18 / 2
slope = -9
Slope between (-6, -9) and (-2, -18):
slope = (-18 - (-9)) / (-2 - (-6))
slope = -9 / 4.0
slope = -2.25
Slope between (-2, -18) and (8, -63):
slope = (-63 - (-18)) / (8 - (-2))
slope = -45 / 10
slope = -4.5
Slope between (8, -63) and (16, -99):
slope = (-99 - (-63)) / (16 - 8)
slope = -36 / 8
slope = -4.5
The slopes for the first three pairs of points (-9, -2.25, -4.5) match, indicating a consistent linear relationship.
However, the slope between the last two points is -4.5, not -4.25 like the others.
Therefore, the point (16, -99) is not a perfect fit.
Removing the point (16, -99), we have four remaining data points:
(-8, 9), (-6, -9), (-2, -18), and (8, -63).
To find the slope-intercept equation for the linear model that passes through these four points, we can use the formula:
y = mx + b
Using the slope formula with two of the remaining points:
-9 = m(-6) + b
-18 = m(-2) + b
Solving these two equations simultaneously, we find:
m = -9/4
b = 9/2
So the slope-intercept equation for the linear model is:
y = (-9/4)x + 9/2
The practical meaning of the y-intercept (9/2) is that when the previous day's change in the Dow Jones is 0 points, the net approval rating for the president of the United States is expected to be 9/2 percentage points, or 4.5 percentage points.
The practical meaning of the slope (-9/4) is that for every 1-point increase in the previous day's change in the Dow Jones, the net approval rating for the president of the United States is expected to decrease by 9/4 percentage points, or 2.25 percentage points.
For similar question on linear model.
https://brainly.com/question/31265606
#SPJ11
The vertices of a square are A (-6, 4), B(-1, 6), C(1, 1), and D( -4, -1). How long is the diagonal?
1. √29 units
2. 2√29 units
3. √58 units
4. 2√58 units
Answers
Answer:
\( \sqrt{58} \)
XY is a translation of XY.
Write the translations as a rule applied to each coordinate (x,y).
PLEAS WITH THIS QUESTION HELP ASAP

Answers
Given:
The graph of a translation. X'Y' is a translation of XY.
To find:
The rule of the translation.
Solution:
Let the rule of the translation be
\((x,y)\to (x+a,y+b)\) ...(i)
So, we need to find the value of a and b.
From the given graph, it is clear that X(-4,-9) and X'(-1,0).
Using (i), the image of X(-4,-9) is
\(X(-4,-9)\to X'(-4+a,-9+b)\)
We have, X'(-1,0). So,
\(X'(-4+a,-9+b)=X'(-1,0)\)
On comparing both sides, we get
\(-4+a=-1\)
\(a=-1+4\)
\(a=3\)
And,
\(-9+b=0\)
\(b=9\)
So, the missing values in the rule of the translation are 3 and 9 respectively.
Therefore, the rule of translation is \((x,y)\to (x+3,y+9)\).
a boy is 8 years older than his brother. four years from now the boy will be twice as old as his brother. how old is each boy now
Answers
Answer:
boy would be 12 brother would be 6
Step-by-step explanation:
8+4 = 12
---- brother = 6
2
i never understand these

Answers
Let’s first find the area of the bigger rectangle:
To find area you just multiply l•w, or length•width.
For the big rectangle, the length is 20, and the width is 5. When these are multiplied you get 100.
So, the area of that first shape is 100. Now we have to find the others, using the same process!
The small rectangle has a length width of 4, but the length is not there.
In order to find the length, you have to use the bigger rectangles length, but subtract the left and right sides (the 5’s).
So it looks like this;
20-5-5 = 10!
The length is 10 and the width is 4. Now just multiply!
10•4 = 40
Now for the last shapes. Typically with a triangle you would divide it by two, but since you already have to triangles, you can combine them to make like a square shape.
So, once again, you do l•w:
5•4=20
(no further steps since you have two triangles already)
Now that we have the area of every individual shape, you just add them all!
100+40+20= 160
Your answer is 160 (but make sure to add in your unit, and when finding area you have to add the little 2)
So it’s 160in.^2
What is the area of one of the triangular faces? in 2 4 in. 3 in. 7 in. 7 in. 5 in. 4 in. 5 in.
Answers
Answer:
55
Step-by-step explanation:
(L5) To form a triangle, the sum of the lengths of any two line segments must be __________ than the length of the third side.The set of line segments __________ meet the requirements to form a triangle.
Answers
To form a triangle, the sum of the lengths of any two line segments must be greater than the length of the third side. This is known as the triangle inequality theorem. For example, if we have line segments with lengths of 5, 7, and 10 units, we can add the first two lengths (5+7=12) and compare it to the length of the third side (10). Since 12 is greater than 10, we can form a triangle with these line segments.
On the other hand, if we have line segments with lengths of 3, 6, and 10 units, we can add the first two lengths (3+6=9) and compare it to the length of the third side (10). Since 9 is not greater than 10, we cannot form a triangle with these line segments.
Therefore, the set of line segments that do not meet the requirements to form a triangle are those where the sum of any two lengths is equal to or less than the length of the third side. It is important to remember the triangle inequality theorem when working with triangles, as it is a fundamental rule that determines if a set of line segments can form a triangle or not.
learn more about triangles here: brainly.com/question/11070154
#SPJ11
Find the measurement parallelogram.
I need help please, thank you.
I need explanation

Answers
Answer:
2.) 145°
4.) 50°
Step-by-step explanation:
2.) First find the measure of Angle Y, since they are supplementary;
∠Z + ∠Y = 180
35 + ∠Y = 180
∠Y = 180 - 35
∠Y = 145°
So ∠X would be 145° as well
4.) First find the measure of Angle F, since they are supplementary;
∠C + ∠F = 180
130 + ∠F = 180
∠F = 180 -130
∠F = 50°
So ∠E would be 50°
(I didn't explain it much in detail, since this question is similar to the previous that i answered :)
Hope this helps!
Find the annual rate of interest.
Principal = 7800
Period = 7
Total amount = 11349
Answers
Answer:
sup
Step-by-step explanation:
a bridge hand consists of 13 cards from a deck of 52. find the probability that a bridge hand includes exactly 4 aces and exactly 3 kings.
Answers
The probability that a bridge hand includes 4 acres and exactly 3 kings is 0.028%
To find the probability of getting exactly 4 aces and 3 kings in a bridge hand, we can use the following formula:
P(4 aces and 3 kings) = (number of ways to get 4 aces and 3 kings) / (number of ways to select 13 cards from a deck of 52)
To calculate the numerator, we can first find the number of ways to choose 4 aces from the 4 available in the deck, and then the number of ways to choose 3 kings from the 4 available in the deck. The remaining 6 cards can be any of the 44 non-ace, non-king cards. Therefore:
Number of ways to get 4 aces and 3 kings = (4 choose 4) x (4 choose 3) x (44 choose 6) = 1 x 4 x 44,380,776 = 177,523,104
To calculate the denominator, we can find the total number of ways to choose any 13 cards from the 52-card deck:
Number of ways to select 13 cards from a deck of 52 = (52 choose 13) = 635,013,559,600
Therefore, the probability of getting exactly 4 aces and 3 kings in a bridge hand is:
P(4 aces and 3 kings) = (number of ways to get 4 aces and 3 kings) / (number of ways to select 13 cards from a deck of 52) = 177,523,104 / 635,013,559,600 = 0.0002799 or approximately 0.028%.
To know more about the "probability": https://brainly.com/question/24756209
#SPJ11
corresponding angles are congruent =. which angle corresponds with 3
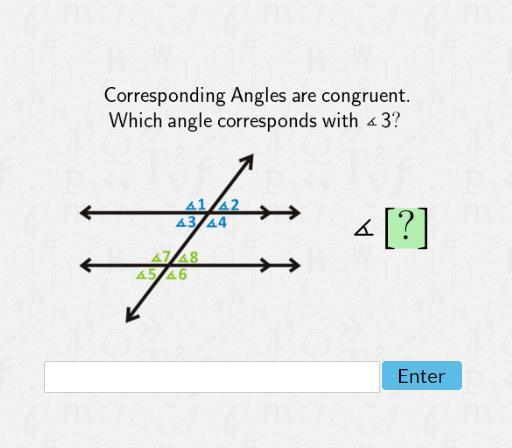
Answers
The angle that corresponds to 3 is angle 5
How to determine the angle that corresponds to 3?Corresponding angles are angles that are at the same relative position between parallel lines and transversal
These angles are congruent
From the figure, we have:
Angle 3 and Angle 5 are in the same relative position
Hence, the angle that corresponds to 3 is angle 5
Read more about corresponding angles at:
https://brainly.com/question/24839702
#SPJ1
Find the solution point(s) for the system of equations given by y = 2x^2 + 5x – 10 and 4x – y = –11
Answers
Answer:
the solution points for the system of equations are (3, 25) and (-7/2, -7).
Step-by-step explanation:
We can solve this system of equations using substitution or elimination. Here, we will use the substitution method:
Substitute y = 2x^2 + 5x - 10 into the second equation:
4x - (2x^2 + 5x - 10) = -11
Simplifying the left side of the equation:
4x - 2x^2 - 5x + 10 = -11
Rearranging the terms:
2x^2 - x + 21 = 0
Using the quadratic formula:
x = (-(-1) ± sqrt((-1)^2 - 4(2)(21))) / 2(2)
x = (1 ± sqrt(169)) / 4
x = (1 ± 13) / 4
Simplifying:
x = 3 or x = -7/2
Now, substitute each value of x back into one of the original equations to find the corresponding value(s) of y:
For x = 3:
y = 2(3)^2 + 5(3) - 10 = 25
So one solution point is (3, 25).
For x = -7/2:
y = 4(-7/2) + 11 = -7
So the other solution point is (-7/2, -7).
Therefore, the solution points for the system of equations are (3, 25) and (-7/2, -7).
Can I please get some help on this xD I think its equal but I dunno someone please confirm the surface area is equal

Answers
Kirsty is making a fruit drink for 9 people. How many oranges does she use?
Answers
Answer:
9
Step-by-step explanation:
Which of the following best describes the graph shown below?
A. This is the graph of a one-to-one function.
B. This is the graph of a linear function.
C. This is the graph of a function, but it is not one-to-one.
D. This is not the graph of a function.

Answers
I just learnt about this recently
I am from India
Good to hell u
What is the distance between points F(2, 9) and G(4, 14)? Round to the nearest whole number.
Answers
Answer:
5
Step-by-step explanation:
You decide to pull a 150-kg sled across an icy pond that is 24 m across. You start pulling with a constant force of 200 N. When you get halfway across the pond, you hear the ice cracking and decide to increase your force so that it increases linearly with distance, eventually reaching 500 N when you get to the other side of the pond. How fast is the sled moving when you reach the other side
Answers
The sled is moving at approximately 9.38 m/s when you reach the other side of the pond.
To solve this problem, we can use the concept of work and energy. The work done on an object is equal to the force applied multiplied by the distance over which the force is applied. In this case, the work done is equal to the change in kinetic energy of the sled.
Let's break down the problem into two parts: when you're pulling with a constant force of 200 N and when you're pulling with a force increasing linearly from 200 N to 500 N.
First, let's calculate the work done during the first part of the motion, where the force is constant. The work done is given by:
Work = Force × Distance
Work = 200 N × (24 m/2)
Work = 200 N × 12 m
Work = 2400 N·m
The work done during this part is 2400 N·m. This work contributes to the sled's change in kinetic energy.
Next, let's calculate the work done during the second part of the motion, where the force is increasing linearly. The average force during this part is (200 N + 500 N) / 2 = 350 N. The distance covered during this part is 24 m/2 = 12 m. The work done is given by:
Work = Average Force × Distance
Work = 350 N × 12 m
Work = 4200 N·m
The total work done on the sled is the sum of the work done in both parts:
Total Work = Work (constant force) + Work (linearly increasing force)
Total Work = 2400 N·m + 4200 N·m
Total Work = 6600 N·m
Now, we can equate the work done to the change in kinetic energy:
Total Work = Change in Kinetic Energy
6600 N·m = (1/2) × mass × (final velocity)^2
Here, the mass of the sled is 150 kg. We need to solve for the final velocity.
Rearranging the equation:
(final velocity)^2 = (2 × Total Work) / mass
(final velocity)^2 = (2 × 6600 N·m) / 150 kg
(final velocity)^2 = 88 N·m/kg
final velocity = √(88 N·m/kg)
final velocity ≈ 9.3808 m/s
Therefore, the sled is moving at approximately 9.38 m/s when you reach the other side of the pond.
To know more about sleds, refer here:
https://brainly.com/question/31309528#
#SPJ11
Need NOW help FAST PLS . hs geometry

Answers
Hope you could get an idea from here.
Doubt clarification - use comment section.
Solve for x:
7/2x + 1/2 = 3
Give your answer in its simplest form.
Answers
X=5/7
please note on step 3 that i divided both sides by the coefficient of X

Answer:
7/5 or 1.4
Step-by-step explanation:
7/2x+1/2=3
CLT
7/2x=3-1/2
7/2x=5/2
cross multiply
10x=14
divide both sides by 10
10x/10=14/10
x=14/10
x=1.4 or 7/5
