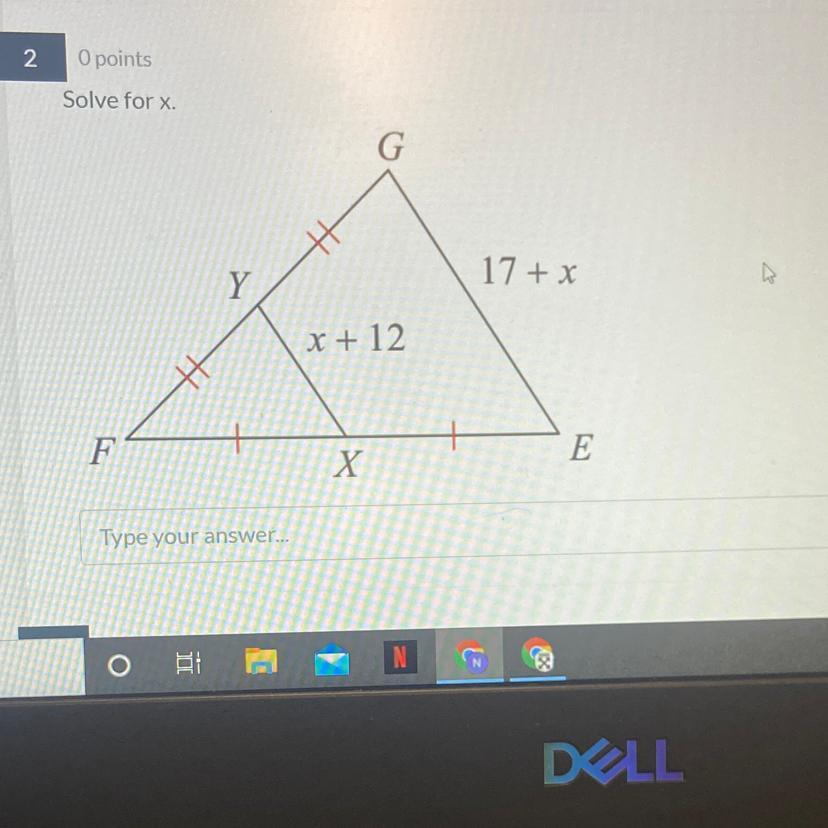
Answers
Answer:
x = -7Step-by-step explanation:
XY is the midsegment of the given triangle.
XY = 1/2GE, as per definition of midsegment
Substitute and solve for x:
x + 12 = 1/2(17 + x)2x + 24 = x + 172x - x = 17 - 24x = - 7X and Y are midpoints
2XY=GE2(x+12)=x+172x+24=x+17x=17-24x=-7Related Questions
Evaluate the line integral x dy + (x - y)dx, where C is the circle x² + y² = 4 oriented clockwise using: a) Green's Theorem (3 b) With making NO use of Green's Theorem, rather directly by parametrization.
Answers
a) Using Green's Theorem, the line integral of the given vector field around the clockwise-oriented circle is zero.
Green's Theorem states that for a vector field F = P(x, y)i + Q(x, y)j, the line integral of F around a simple closed curve C is equal to the double integral of (dQ/dx - dP/dy) over the region R enclosed by C. Since the circle x² + y² = 4 encloses the region R, the double integral of 2 over R is zero. Consequently, the line integral of the given vector field around C is zero.
b) Directly parametrizing the circle, we can evaluate the line integral without Green's Theorem.
For the clockwise-oriented circle x² + y² = 4, we can parametrize it as x = 2cos(t) and y = 2sin(t), where t goes from 0 to 2π. Substituting these parametric equations into the given vector field, we have x dy + (x - y)dx = (2cos(t))(2cos(t)dt) + ((2cos(t)) - (2sin(t)))(-2sin(t)dt). Simplifying the expression and integrating over the interval [0, 2π] with respect to t, we can calculate the value of the line integral.
a) By applying Green's Theorem, which relates line integrals to double integrals, we can determine the value of the line integral directly. The theorem allows us to evaluate the line integral by computing a double integral over the region enclosed by the curve, ultimately simplifying the calculation.
b) Alternatively, we can directly parametrize the given curve and substitute the parametric equations into the vector field to obtain an expression solely in terms of the parameter. By integrating this expression over the parameter range, we can evaluate the line integral without relying on Green's Theorem.
Learn more about Green's Theorem here: brainly.com/question/30080556
#SPJ11
Can anyone help I keep getting it wrong

Answers
Answer:
C
Step-by-step explanation:
What is the domain of g?

Answers
Answer: The domain of G is 4
Step-by-step explanation:
The domain is the set of all inputs that makes the function definable. The domain is always represented on the x axis.So looking at g on its x axis you see 4. So the domain is 4.
Answer:
4
Step-by-step explanation:
on what issues did the reformer ignatius of loyola focus
Answers
Ignatius of Loyola, the Spanish priest and theologian who founded the Society of Jesus (Jesuits) in the 16th century, focused on several key issues during the period of the Counter-Reformation.
These issues can be broadly categorized into spiritual, educational, and institutional reforms.
Spiritual Reforms: Ignatius emphasized the importance of personal piety and spiritual discipline. He promoted the practice of spiritual exercises, including meditation, prayer, and self-examination, to cultivate a deep and intimate relationship with God. Ignatius encouraged individuals to reflect on their sins and seek forgiveness through confession and penance.
Educational Reforms: Ignatius recognized the power of education in shaping individuals and society. He established schools and universities to provide a comprehensive education that combined intellectual rigor with spiritual formation. The Jesuits placed great emphasis on academic excellence, encouraging critical thinking, the pursuit of knowledge, and the integration of faith and reason.
Pastoral Reforms: Ignatius focused on improving the quality of pastoral care and religious instruction. He trained his followers to be skilled preachers and spiritual directors, equipping them to guide and support individuals in their spiritual journey. Ignatius also emphasized the importance of catechesis, ensuring that people received proper religious education and understood the teachings of the Catholic Church.
Missionary Work: Ignatius and the Jesuits had a strong missionary zeal. They undertook extensive missionary endeavors, particularly in newly discovered territories during the Age of Exploration. They sought to bring Christianity to non-Christian lands and convert indigenous populations to Catholicism. The Jesuits established missions, schools, and hospitals in various parts of the world, playing a significant role in spreading Catholicism.
Overall, Ignatius of Loyola's reforms aimed to strengthen and revitalize the Catholic Church in response to the challenges posed by the Protestant Reformation. His focus on personal spirituality, education, pastoral care, and missionary work contributed to the renewal and expansion of the Catholic Church during the Counter-Reformation.
Learn more about expansion here:
https://brainly.com/question/30642466
#SPJ11
I NEED A GOOD ANWSER
How many 6 inch photos will fit inside 48 inches?
(please write your answer and explain.
Answers
Answer:
8
Step-by-step explanation:
48/6 = 8
If this is what the question is asking.. just divide the space by the size of photos
3.once we moved from the 5-kingdom scheme to the 3-domain scheme, which two kingdom names were completely eliminated?
Answers
The three domains are the Archaea, the Bacteria, and the Eukary.
What is 5 kingdom scheme?R.H. Whittaker proposed the five kingdom division in 1969. Based on traits including cell structure, manner of nutrition, source of nutrition, and body organization, the five kingdoms were created. The Kingdoms Monera, Protista, Fungi, Plantae, and Animalia are all included in it. Depending on factors like cell structure, mode of nutrition, mode of reproduction, and body organization, living things are categorized into five different kingdoms: Protista, Fungi, Plantae, Animalia, and Monera.The conclusions have since become accepted, leading to replacement of the kingdom Monera with the two domains Bacteria and Archaea.learn more about kingdom scheme click here:
https://brainly.com/question/1413097
#SPJ4
Do the ratios 21:28 and 6:8 form a proportion?
Answers
Answer:
Yes
Step-by-step explanation:
they are both equal to 3:4
21:28 can be reduced by 7
21/7=3
28/7=4
and 6:8 can be reduced by 2
6/2=3
8/2=4
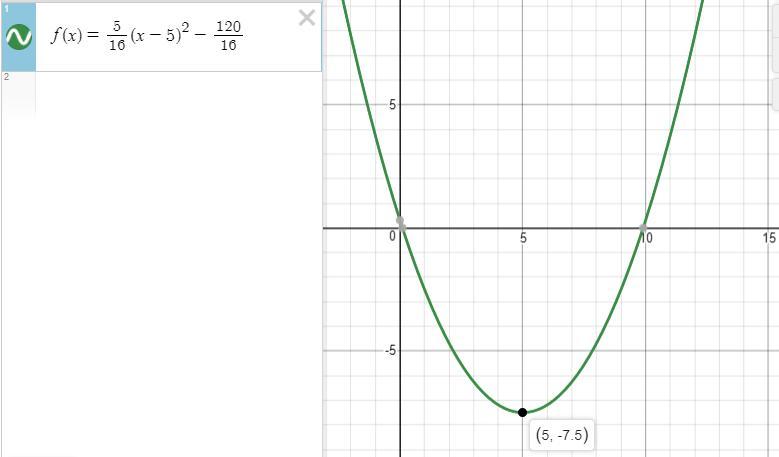
Please answer the question will mark brainliest.., graph the equation

Answers
Functions can be represented as equations, tables and graphs
The equation represents a parabola, that has a vertex of (5, -7.5)
ParabolaThe equation of a parabola is represented as:
\(y = a(x - h)^2 + k\)
Where (h,k) represents the vertex
Rewriting the equationThe equation is given as:
\(f(x) = \frac{5}{16}(x -1)(x - 9)\)
Expand the above equation
\(f(x) = \frac{5}{16}(x^2 -x - 9x + 1)\)
Evaluate the common factors
\(f(x) = \frac{5}{16}(x^2 -10x + 1)\)
Expand
\(f(x) = \frac{5}{16}(x^2 -10x) + \frac{5}{16}\)
Add and subtract k from the bracket
\(f(x) = \frac{5}{16}(x^2 -10x + k - k) + \frac{5}{16}\)
The value of k is calculated as follows:
\(k = (\frac{10}{2})^2\)
\(k = 25\)
So, we have:
\(f(x) = \frac{5}{16}(x^2 -10x + k - k) + \frac{5}{16}\)
\(f(x) = \frac{5}{16}(x^2 -10x + 25) -\frac{5}{16} \times 25 + \frac{5}{16}\)
\(f(x) = \frac{5}{16}(x^2 -10x + 25) -\frac{125}{16} + \frac{5}{16}\)
Take LCM
\(f(x) = \frac{5}{16}(x^2 -10x + 25) +\frac{-125 + 5}{16}\)
\(f(x) = \frac{5}{16}(x^2 -10x + 25) -\frac{120}{16}\)
Factorize the expression in the bracket
\(f(x) = \frac{5}{16}(x -5)^2 -\frac{120}{16}\)
So, we plot the graph of \(f(x) = \frac{5}{16}(x -5)^2 -\frac{120}{16}\).
See attachment for the graph
Read more about parabolas at:
https://brainly.com/question/4061870
Write the first five terms of the arithmetic sequence. First term: -10 and common difference: 2
Answers
Answer:
The first five terms of the arithmetic sequence.
-10 , -8 , -6 , -4 ,-2 ..........
Step-by-step explanation:
Explanation
Given that the first term is -10 and common difference d = 2
we know that the sequence in A.P
a ,a+d ,a+2d,a+3d ,a+4d........... are in AP
-10, -10+2, -10+2(2), -10+3(2) , -10+4(2)..................
-10 , -8 , -6 , -4 ,-2 ..........
Final answer:-
The first five terms of the arithmetic sequence.
-10 , -8 , -6 , -4 ,-2 ..........
20/24 equals 45/50 true or false
Answers
bring the fractions to a common denominator
\(undefined\)Use the equation p=b-3 to find the value of p when b = 8
Answers
Answer:
5
Step-by-step explanation:
p=(8)-3
p=5
Answer:
p=8-3
p=5
Step-by-step explanation:
1 2 3 4 5 6 7 8 9 10
TIME REMAINING
58:17
Which graph represents viable values for y = 2x, where x is the number of pounds of rice scooped and purchased from a bulk bin at the grocery store and y is the total cost of the rice?
On a coordinate plane, a straight line with a positive slope begins at point (0, 0), and ends at point (2.5, 5).
On a coordinate plane, blue diamonds appear at points (0, 0), (1, 2), (2, 4).
On a coordinate plane, a straight line with a positive slope begins at point (negative 2.5, negative 5), crosses the x- and y-axis at point (0, 0), and ends at point (2.5, 5).
On a coordinate plane, blue diamonds appear at points (negative 2, negative 4), (negative 1, negative 2), (0, 0), (1, 2), (2, 4).
Answers
The graph that represents viable values for y = 2x is Option A.
What is a Straight Line Function ?A straight line function is given by y = mx +c , where m is the slope and c is the y intercept.
The given equation is y = 2x
here m = 2
x is the number of pounds of rice scooped and purchased from a bulk bin
y is the total cost of the rice
as both the data cannot be negative , Option C , D is out of choice
The Option 1 represents a straight line and it starts at the origin which is satisfied by y = 2x as y = 0 , at x = 0
ends at point (2.5, 5) giving a slope of m =2 ,
Therefore , The graph that represents viable values for y = 2x is Option A.
To know more about Straight Line equation
https://brainly.com/question/959487
#SPJ1
Gabriel is building a flower box for his garden. He is building a cube
without a top so that he can fill it with soil. He needs to calculate
the surface area to determine how much wood he needs. The
length of the box is 3 feet.
Which expression will give him the surface area?
O 3x3x6
O 3x3x3
O 3x3x5
O 3+3+3

Answers
Answer: 3*3*5 because each square is 3 by 3 and there are 5 faces which you need wood on -> there is no top face.
3
Select the correct answer.
The graph of the rational function is shown.
16
14
-6
-4
-2
0
4
2
6
MA
which graph is the graph of g(x)=-f(x)
Answers
Answer:
0,-2,-4
Step-by-step explanation:
pls help...
solve for x in the following...pls explain
a)7x+5=3x-1
b)5x+12=3x+14
Answers
Answer:
a) x = -1.5
b) x = 1
Step-by-step explanation:
For problem a, you can start by subtracting 3x from both sides to gather all the like terms together:
7x + 5 = 3x - 1
-3x -3x
4x + 5 = -1
Next, to get the coefficients on one side, you subtract 5 from both sides:
4x + 5 = -1
-5 -5
4x = -6
Now, you divide by 4 on both sides to isolate x:
x = -6/4 = -1.5 --- > x = -1.5
For problem b, you start by subtracting 3x from both sides(kinda like problem a):
5x + 12 = 3x + 14
-3x -3x
2x + 12 = 14
Next, you can subtract 12 from both sides, isolating the "x term".
2x + 12 = 14
-12 -12
2x = 2
Lastly, you can divide by 2 to get x:
x = 1
1:
\(7x +5=3x-1\\7x+5-3x=-1\\7x-3x=-1-5\\4x= -1-5\\4x= -6\\x=-\frac{6}{4} (en donde ambos se divide entre 4)\\Respuesta / x=-\frac{3}{2}\)
2:
\(5x+12=3x + 14\\5x+12-3x=16\\5x-3x=16-12\\2x= 16-12\\2x= 4\\x=4/2\\( se divide entre 2)x= 2\)
Find an equation of the tangent line to the astroid at the (-3√3, 1).
x²/³ + y²/³ = 4
Answers
The equation of the tangent line to the astroid at the point (-3√3, 1) is: y = -(3√3)^(1/3)x - 3(3√3)^(1/3) + 1
To find the equation of the tangent line to the astroid at the point (-3√3, 1), we need to first find the slope of the tangent line.
We can do this by taking the derivative of the equation of the astroid with respect to x, and then evaluating it at the point (-3√3, 1).
Taking the derivative of x²/³ + y²/³ = 4 with respect to x, we get:
(2/3)x^(-1/3) + (2/3)y^(-1/3) * dy/dx = 0
Solving for dy/dx, we get:
dy/dx = (-x^(1/3))/y^(1/3)
Substituting x = -3√3 and y = 1, we get:
dy/dx = (-(-3√3)^(1/3))/(1^(1/3)) = -(3√3)^(1/3)/1
So the slope of the tangent line at the point (-3√3, 1) is -(3√3)^(1/3).
Now we can use the point-slope form of the equation of a line to find the equation of the tangent line. The point-slope form is:
y - y1 = m(x - x1)
Substituting x1 = -3√3, y1 = 1, and m = -(3√3)^(1/3), we get:
y - 1 = -(3√3)^(1/3)(x + 3√3)
Simplifying, the equation of the tangent line to the astroid at the point (-3√3, 1) is:
y = -(3√3)^(1/3)x - 3(3√3)^(1/3) + 1
Learn more about derivatives here: brainly.com/question/25324584
#SPJ11
Natasha walked from the library to the grocery store then to her house. The diagram shows the top of the locations of these three places and their distances from each other.
Which measurement is closest distance in miles from Natasha’s house to the library?
A. 2.6 mi
B. 1.9 mi
C. 1.4 mi
D. 2.3 mi
PLEASE HELP!!!!
Answers
B
Step-by-step explanation:
a^2+b^2=c^2
1.7^2+0.9^2=x^2
2.89+0.81=x^2
3.7=x^2
x=about 1.9
Please match the following

Answers
x7/x4 = x^3
x^-3 = 1/x^3
x^0 = 1
x^4/x^3 = x
let me know if i got them right! :)
What is the x-coordinate of the point that divides the directed line segment from J to K into a ratio of 2:5? m 4 m ][xz – xı) + x, -4 -2 2 4

Answers
Answer:
2
Step-by-step explanation:
im sure its 2 i hope this helps
Help me pls I’ll give brainliest pls dont answer if you don’t know

Answers
Answer:
4 - 2x = 36
Ste4p-by-step explanation:
We have to add the ones with the same variables.
-17 + 21 = 4
-5x + 3x = -2x
4 - 2x = 36
Which operations are present in the algebraic expression 3x + 2 ?
Answers
The expression 3x²+x+5 is the sum of 3 terms and coefficients are 3 and 1 therefore, Neither Joanna nor Linne is correct.
What is an algebraic expression?
An algebraic expression is consists of variables, numbers with various mathematical operations,
The given expression is,
3x²+x+5.
According to Joanna, the entire expression is the sum of 4 terms.
and according to Linne the coefficients are 3 and 0.
Since, The expression is the sum of 3 terms:
Square power of x, x and a constant 5.
Also, the coefficient of x² is 3 and coefficient of x is 1.
Therefore, the Joanna and Lienna both are wrong.
To know more about Algebraic expression on:
brainly.com/question/19245500
#SPJ1
Mr. T's Tea store has two kinds of tea. Tea A costs $9 per pound and Tea B cost $6 per pound. How many pounds of each should be combined to obtain 150 pounds of tea worth $8 per pound?
Answers
Answer:
y=447.3 pounds
x= 297.3 pounds
Step-by-step explanation:
Step one:
given data
Tea A costs $9 per pound and
Tea B cost $6 per pound.
let the number of pounds of Tea A be x
and for Tea B be y pounds
The total cost of the mixture = $8 per pound
hence
9x+6y=8---------1
The total weight of the mixture
150 pounds
x+y=150-----------2
Step two:
9x+6y=8---------1
x+y=150---------2
from eqn 2 x=150-y
put x= 150-y in eqn 1
9(150-y)+6y=8---------1
1350-9y+6y=8
1350-8=9y-6y
1342=3y
divide both sides by 3
y= 1342/3
y=447.3 pounds
put y= 447.3 in eqn 2
x+447.3= 150
x= 150-446=7.3
x= -297.3
x= 297.3 pounds
Joaquin used two types of flour in a muffi n recipe. How much flour did he use in all? Solve any way you choose.
Answers
Answer:
Total flour used = 3 1/6 c
Step-by-step explanation:
Whole wheat flour = 1 1/2 c
Buckwheat flour = 1 2/3 c
How much flour did he use in all?
Total flour used = Whole wheat flour + buckwheat flour
= 1 1/2 c + 1 2/3 c
= 3/2 c + 5/3 c
= (9c + 10c) / 6
= 19c/6
= 3 1/6 c
Total flour used = 3 1/6 c

Consider the vector field F(x,y,z)=(−2y,−2x,7z)F(x,y,z)=(−2y,−2x,7z). Show that F is a gradient vector field F=∇V by determining the function V which satisfies V(0,0,0)=0.
Answers
To show that the vector field F(x, y, z) = (-2y, -2x, 7z) is a gradient vector field, we need to find a scalar function V(x, y, z) such that its gradient, ∇V, is equal to F. We can determine the function V by integrating the components of F with respect to their respective variables.
Let's find the function V(x, y, z) by integrating the components of F(x, y, z) = (-2y, -2x, 7z) with respect to their variables.
∫-2y dx = -2xy + g(y, z)
∫-2x dy = -2xy + h(x, z)
∫7z dz = 7/2 z^2 + k(x, y)
We can see that -2xy is a common term in the first two integrals. Similarly, we observe that there are no common terms between the first and third integrals, as well as the second and third integrals. Therefore, we can assume that g(y, z) = h(x, z) = 0, since they will cancel out in the subsequent calculations.
Now, we can rewrite the integrals:
∫-2y dx = -2xy + C1(y, z)
∫-2x dy = -2xy + C2(x, z)
∫7z dz = 7/2 z^2 + C3(x, y)
By comparing these integrals with the components of the gradient vector, we can conclude that ∇V = (-2y, -2x, 7z), where V(x, y, z) = -xy + 7/2 z^2 + C.
To determine the constant C, we use the condition V(0, 0, 0) = 0:
V(0, 0, 0) = -(0)(0) + 7/2 (0)^2 + C = 0
C = 0
Therefore, the function V(x, y, z) that satisfies V(0, 0, 0) = 0 is V(x, y, z) = -xy + 7/2 z^2. Thus, the vector field F(x, y, z) = (-2y, -2x, 7z) is indeed a gradient vector field F = ∇V.
Learn more about scalar function here
https://brainly.com/question/32616203
#SPJ11
Will give brainliest if correct.

Answers
Answer:
slope is 5, y intercept is -7
Step-by-step explanation:
In the form y=mx+c, m is the slope and c is the y-intercept.
Rearrange the formula to fit this form:
5x-y=7
-y=7-5x
y=5x-7
∴m(slope)=5
∴c(y-intercept)=-7
brainliest+100 points


Answers
Answer:
Page 1
1)
a) - 5x^4+3
Degree: 4
Number of terms: 2
b) 5x² + 30x+25
Degree: 2
Number of Terms: 3
c) 16r^4p
Degree: 4
Number of Terms: 1
d) 9m²n + 12mn +4m -6n+19
Degree:2
Number of Terms:5
Note:
Degree: the highest exponent of the variable x)
Number of terms: It is either a single number or variable, or numbers and variables multiplied together. Terms are separated by + or - signs, or sometimes by divide
Page 2:
Add or subtract the following polynomials.
a) (3p^3+6p^2+14p)+(-5p^3-2p+8p^2
opening bracket
3p^3+6p^2+14p+(-5p^3-2p+8p^2)
3p^3+6p^2+14p-5p^3-2p+8p^2
Combining like terms
-2p^3 +14p^2+12p
b) (7y^3-5y)-(5y-7y^3)
Opening bracket
7y^3-5y-5y+7y^3
Combining like terms
14y^3-10y
c) (6z^4+15-7z^3)+(-2z^4+8z^3-5z^5)
Opening bracket
6z^4+15-7z^3-2z^4+8z^3-5z^5
-5z^5 +4z^4+1z^3+15
d) (-3n²-14n+1)-(-7n+2-6n²)
Opening bracket
-3n²-14n+1+7n-2+6n²
3n²-7n-1
e) (7b^3-14-8b^4) − (−3b^4+7b³ +4)
Opening bracket
7b^3-14-8b^4+3b^4-7b³-4
-5b^4-18
f) (-3n^2-4n+2n⁴) + (3n^2+ 19n-7n^4)
Opening bracket
-3n^2-4n+2n⁴+3n^2+ 19n-7n^4
-5n⁴+15n
Answer:
Page 1
1)
a) - 5x^4+3
Degree: 4
Number of terms: 2
b) 5x² + 30x+25
Degree: 2
Number of Terms: 3
c) 16r^4p
Degree: 4
Number of Terms: 1
d) 9m²n + 12mn +4m -6n+19
Degree:2
Number of Terms:5
Note:
Degree: the highest exponent of the variable x)
Number of terms: It is either a single number or variable, or numbers and variables multiplied together. Terms are separated by + or - signs, or sometimes by divide
Page 2:
Add or subtract the following polynomials.
a) (3p^3+6p^2+14p)+(-5p^3-2p+8p^2
opening bracket
3p^3+6p^2+14p+(-5p^3-2p+8p^2)
3p^3+6p^2+14p-5p^3-2p+8p^2
Combining like terms
-2p^3 +14p^2+12p
b) (7y^3-5y)-(5y-7y^3)
Opening bracket
7y^3-5y-5y+7y^3
Combining like terms
14y^3-10y
c) (6z^4+15-7z^3)+(-2z^4+8z^3-5z^5)
Opening bracket
6z^4+15-7z^3-2z^4+8z^3-5z^5
-5z^5 +4z^4+1z^3+15
d) (-3n²-14n+1)-(-7n+2-6n²)
Opening bracket
-3n²-14n+1+7n-2+6n²
3n²-7n-1
e) (7b^3-14-8b^4) − (−3b^4+7b³ +4)
Opening bracket
7b^3-14-8b^4+3b^4-7b³-4
-5b^4-18
f) (-3n^2-4n+2n⁴) + (3n^2+ 19n-7n^4)
Opening bracket
-3n^2-4n+2n⁴+3n^2+ 19n-7n^4
-5n⁴+15n
Step-by-step explanation:
HELP NEEDED ASAP! GIVING BRAINLIEST

Answers
Answer:
C (u=5)
B ( angle 4)
Step-by-step explanation:
how many solutions does y=x+4 and y=2x+4 have?
Answers
Answer:
x = 0
Step-by-step explanation:
y = x + 4 and y = 2x + 4
Let's solve
x + 4 = 2x + 4
-x + 4 = 4
-x = 0
x = 0
So, there is only one solution is x = 0
The two lines have the same y-intercept, and therefore, that’s one solution there. But because the line will never cross other than at y=4, the two equations will only have 1 solution.
Hope this helped!
What is 2-3-7-9-6-7-8-6-5-7-7
Answers
Answer:-61
Step-by-step explanation:
Answer:
2-3-7-9-6-7-8-6-5-7-7=-63
Step-by-step explanation:
Hope it helps!!!
;}
Directions: Follow these steps to complete the activity.
Step 1:As you go about your daily activities during the week, think about how many times you 'round' numbers without even thinking about it. Do you round at the grocery store? Do you round when you are counting points earned playing video games? Do you round numbers when you are estimating time?
Step 2: After you think about how you round numbers (or time), then ask a family member how they use rounding in everyday activities.
Step 3: Write a paragraph telling about when and how you or a family member rounds numbers in everyday activities.Directions: Follow these steps to complete the activity.
Step 1:As you go about your daily activities during the week, think about how many times you 'round' numbers without even thinking about it. Do you round at the grocery store? Do you round when you are counting points earned playing video games? Do you round numbers when you are estimating time?
Step 2: After you think about how you round numbers (or time), then ask a family member how they use rounding in everyday activities.
Step 3: Write a paragraph telling about when and how you or a family member rounds numbers in everyday activities.
Answers
Step 1: At the supermarket, I round numbers as I keep track of how much I'm spending to stay on budget. I mentally add up the sum of my purchases to the nearest dollar. Regarding time, I regularly say, "I'm leaving in about 5 minutes" or "dinner will be done in around 10 minutes." When leaving for an appointment, I round up to account for parking and unknown delays, so my appt that is 17 minutes away will be about 20 minutes in my mind. I always round for time estimates.
Step 2: My family reported similar rounding, except when it comes to exercise like running because seconds count!
Step 3: My family and I regularly use rounding when estimating time. We do this without realizing it as we go about our daily activities. We round our expected food purchases as we shop at the supermarket. My parents regularly announce that we are leaving for an event in 10 minutes, when the reality is that it could be 8-12 minutes. We estimate the time it takes to get to activities and appointments, always rounding to a 5 minute interval. We also round for estimated food delivery times when we update each other by saying,"Food should be delivered in 20 minutes." The runners in my family do not round when tracking their times as seconds matter for their personal records.