Answers
Answer:
x = 1
Step-by-step explanation:
You want the value of x in this geometry where secants LJ and LB intercept arcs BJ = 145x and smaller arc MK = 55° to give angle L = 45x.
External angleThe measure of angle L is half the difference of arcs BJ and MK:
L = (BJ -MK)/2
2(45x) = (145x -55)
55 = 55x . . . . . . . . . add 55 -90x
1 = x . . . . . . . . divide by 55
The value of x is 1.
__
Additional comment
We can check the angle relation with x=1:
(145 -55)/2 = 90/2 = 45 . . . . . angle L
<95141404393>
Related Questions
Given the following piecewise function, evaluate limx→−1f(x).
f(x)=
2x^2−3x−2 if x is less than or equal to -1
−x^2+2x+1 if -1
−2x^2−x−1 if x>2
Answers
The solution of the expression will be 3, -2, and -22 respectively.
What is an expression?The mathematical expression combines numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
Given that the expressions are:-
2x²−3x−2 if x is less than or equal to -1
E = 2x²−3x−2
E = 2 (-1) ² - 3 x -1 -2
E = 2 + 3 - 2
E = 3
E = −x²+2x+1 if -1
E = -(-1)² + 2 x -1 + 1
E = -1 - 2 + 1
E = -2
E = −2x²−x−1
E = -2 ( 3 )² - 3 - 1
E = -18 - 3 - 1
E = -22
To know more about an expression follow
https://brainly.com/question/28788290
#SPJ1
2800 people attended a football game. 1260 of the people attending supported the home team, while 1540 supported the visiting team. What percentage of people attending supported the home team?
Answers
Answer:
45% of people attending supported the home team
What information is needed to write the equation of a line in point-slope form?
The location of one ordered pair that lies on the line and the line's slope.
The line's slope and one ordered pair that is not on the line.
The location of one ordered pair on the line and one ordered pair that is not on the line.
The slope of the line and the location of the origin.
Answers
The information that is needed to write the equation of a line in point-slope form is the location of one ordered pair that lies on the line and the line's slope. The correct option is the first option
Point-slope form of the equation of a lineFrom the question, we are to determine the information that is needed to write the equation of a line in point-slope form.
The point-slope form of a line is given as
y - y₁ = m(x - x₁)
Where, (x₁, y₁) is a point on the line
and m is the slope of the line
Thus, in order to write the equation of a line in the point-slope form, the information that are needed are:
1. An ordered pair on the line
2. The slope of the line
Learn more on Point-slope form of the equation of a line here: https://brainly.com/question/11624671
#SPJ1
(a) Calculate a 95% confidence interval for the difference between the proportion of adults older
than 50 and the adults aged between 30-50, who do not support the attack (pD − pI), and
interpret it in this context. We have already checked conditions for you
Answers
95% confident that the true difference in these proportions is between 0.118 and 0.242.
How to calculate a confidence interval for the difference between two proportions?Assuming that the conditions for inference have been met, we can use the following formula to calculate a 95% confidence interval for the difference between two proportions:
(pD - pI) ± zsqrt((pD(1-pD)/nD) + (pI*(1-pI)/nI))
where pD is the proportion of adults older than 50 who do not support the attack, pI is the proportion of adults aged between 30-50 who do not support the attack, nD is the sample size of adults older than 50, nI is the sample size of adults aged between 30-50, and z* is the critical value from the standard normal distribution corresponding to a 95% confidence level, which is approximately 1.96.
Substituting the given values, we get:
(pD - pI) ± 1.96sqrt((pD(1-pD)/nD) + (pI*(1-pI)/nI))
Plugging in the values from the table, we get:
(0.46 - 0.28) ± 1.96sqrt((0.46(1-0.46)/400) + (0.28*(1-0.28)/600))
= 0.18 ± 0.062
So the 95% confidence interval for the difference between the proportion of adults older than 50 and the adults aged between 30-50, who do not support the attack, is (0.118, 0.242). This means that we are 95% confident that the true difference between these two proportions falls within this interval.
Interpreting this in context, we can say that based on the sample data, there is strong evidence to suggest that a higher proportion of adults older than 50 do not support the attack compared to adults aged between 30-50.
Specifically, we can be 95% confident that the true difference in these proportions is between 0.118 and 0.242.
Learn more about statistical inference and hypothesis testing
brainly.com/question/14511153
#SPJ11
Marking brainliest
What else can I write for my last bullet

Answers
sikhism, a religion founded in the 15th century in india, is going through turmoil due to a rapid decline in the number of sikh youths who wear turbans. the tedious task of combing and tying up long hair and a desire to assimilate has led to approximately 25% of sikh youths giving up the turban. a. what is the probability that exactly two in a random sample of five sikh youths wear a turban? (do not round intermediate calculations. round your final answer to 4 decimal places.) b. what is the probability that two or more in a random sample of five sikh youths wear a turban? (do not round intermediate calculations. round your final answer to 4 decimal places.) c. what is the probability that more than the expected number of sikh youths wear a turban in a random sample of five sikh youths? (do not round intermediate calculations. round your final answer to 4 decimal places.) d. what is the probability that more than the expected number of sikh youths wear a turban in a random sample of 10 sikh youths? (do not round intermediate calculations. round your final answer to 4 decimal places.)
Answers
The probability that more than the expected number of Sikh youths wear a turban in a random sample of five is 0.3671 (rounded to 4 decimal places).
a. Using the binomial distribution formula, we can determine the likelihood that two out of a random sample of five Sikh teenagers are turban-wearing:
\(P(X = 2) = (5 pick 2) (5 choose 2) * (0.75)^3 * (0.25)^2\)
"X" indicates the proportion of Sikh adolescents who wear turbans, "5 choose 2" indicates the number of possible methods to select 2 Sikhs from a group of 5, and "0.75" and "0.25" indicate the likelihoods that a Sikh youngster will not be wearing a turban and will be wearing one, respectively.
This expression can be made simpler by using a calculator to become:
P(X = 2) = 10 * 0.421875 * 0.0625 = 0.2659
Hence, 0.2659 percent chance exists that two out of every five Sikh youngsters in a random sample will be turban-wearing (rounded to 4 decimal places).
Using the complement rule, we can determine the likelihood that two or more of a random sample of five Sikh teenagers are wearing turbans:
P(X >= 2) = 1 - P(X 2)
where X is the proportion of young Sikhs who are turban-wearing.
P(X 2) is the likelihood that fewer than 2 of five Sikh teenagers chosen at random will be turban-wearing.
This can be calculated as:
P(X 2) equals P(X = 0) plus P(X = 1).
P(X = 0) = (5 select 0) * (0.75) * (5 select 0) * (0.25) * 0 = 0.2373
P(X = 1) = (5 select 1) * (0.75) * (4 select 1) * (0.25) * 1 = 0.3956
P(X 2) = 0.2373 + 0.3956 = 0.6329 as a result.
We can then compute P(X >= 2) = 1 - 0.6329 = 0.3671 using the complement rule.
Consequently, there is a 0.3671 percent chance that two or more of five Sikh teenagers chosen at random will be turban-wearing (rounded to 4 decimal places).
c. The following formula can be used to determine how many Sikh teenagers in a random sample of five are likely to wear a turban:
E(X) = n * p = 5 * 0.25 = 1.25
Using the cumulative binomial distribution function, we can determine the likelihood that more Sikh teenagers than predicted in a random sample of five wear turbans:
P(X > 1) = 1 - P(X <= 1)
P(X = 1) equals P(X = 0) plus P(X = 1).
P(X = 0) = (5 select 0) * (0.75) * (5 select 0) * (0.25) * 0 = 0.2373
P(X = 1) = (5 select 1) * (0.75) * (4 select 1) * (0.25) * 1 = 0.3956
Therefore,
P(X <= 1) = 0.2373 + 0.3956 = 0.6329
The complement rule can then be used to determine:
P(X > 1)
P(X > 1) = 1 - 0.6329 = 0.3671
Hence, in a random sample of five Sikh adolescents, the likelihood that there are more turban-wearing Sikh youths than expected is 0.3671. (rounded to 4 decimal places).
d. To determine the likelihood that more than predicted will occur.
For similar question on probability.
https://brainly.com/question/29155013
#SPJ11
please help me out, i can not understand this, i will give a brainliest out to whoever can help me

Answers
Answer:
So try 0-6
Step-by-step explanation:
I need help on this PLEASE!!

Answers
Answer:
I can't solve this completely for you, but I'll help you figure it out.
Step-by-step explanation:
All you need to do is choose a number to plug in for x, I'd start with zero and work my way up. Do this for all equations to solve for solutions to your problem.
Solve each system.
[x-3 y =-1 -6 x+19 y =6 ]
Answers
The system of equations [x - 3y = -1 and -6x + 19y = 6] can be solved, resulting in x = -1 and y = 0.
To solve the system of equations [x - 3y = -1 and -6x + 19y = 6], we can use the method of substitution or elimination.
Let's solve it using the method of elimination.
First, we can multiply the first equation by 6 and the second equation by -1 to eliminate the x terms.
This gives us [6x - 18y = -6 and 6x - 19y = -6].
Now, subtracting the first equation from the second eliminates the x terms, leaving us with -y = 0. Solving for y, we find y = 0.
Substituting this value back into the first equation, we get x - 3(0) = -1, which simplifies to x = -1.
Therefore, the solution to the system of equations is x = -1 and y = 0.
Learn more about Equation click here :brainly.com/question/13763238
#SPJ1
Write the phrase as an expression. Then evaluate the expression when x=2 . 8 more than a number x An expression is . The value of the expression is .
Answers
Explanation:
First, we must write the mathematical form for "the product of 8 and a number x":
8
×
x
Then "6 more than this" would be:
(
8
×
x
)
+
6
So, to evaluate for
x
=
5
we substitute
5
for
x
and calculate:
(
8
×
5
)
+
6
→
40
+
6
→
46
HELPPP PLSSSS ITS ALMOST DUE IN 1 HOUR WILL GIVE BRAINLIEST THANKS AND 5 STARSSS
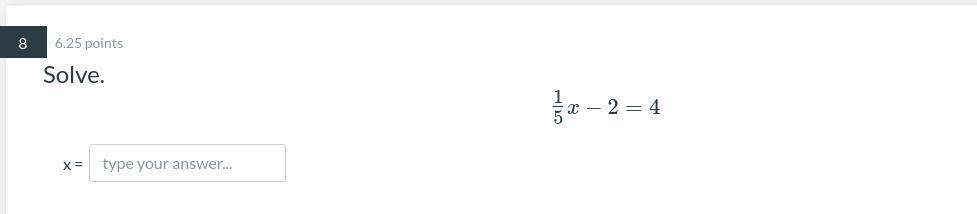
Answers
Answer:
1/30
Step-by-step explanation:
We multiply all the terms by the denominator
-6×5x+1=0
Wy multiply elements
-30x+1=0
We move all terms containing x to the left, all other terms to the right
-30x=-1
x=-1/-30
x=1/30
Find the critical points of the function
f(x)=x^2-9/x^2-4x+3
Use a comma to separate multiple critical points. Enter an exact answer. If there are no critical points, enter ∅ .
x= _______
Answers
The critical value of the function is ∅ is an empty set.
Given data:
To find the critical points of the function f(x) = (x² - 9) / (x² - 4x + 3), we need to find the values of x where the derivative of the function is either zero or undefined.
First, let's find the derivative of f(x) with respect to x:
f'(x) = [(2x)(x² - 4x + 3) - (x² - 9)(2x - 4)] / (x² - 4x + 3)²
Simplifying the numerator:
f'(x) = [2x³ - 8x² + 6x - 2x³ + 4x² - 18x + 8x - 36] / (x² - 4x + 3)²
= (-4x² - 10x - 36) / (x² - 4x + 3)²
To find the critical points, we need to solve the equation f'(x) = 0:
(-4x² - 10x - 36) / (x² - 4x + 3)² = 0
Since the numerator of the fraction can be zero, we need to solve the equation -4x² - 10x - 36 = 0:
4x² + 10x + 36 = 0
We can attempt to factor or use the quadratic formula to solve this equation:
Using the quadratic formula:
x = (-b ± √(b² - 4ac)) / (2a)
In this case, a = 4, b = 10, and c = 36:
x = (-10 ± √(10² - 4 * 4 * 36)) / (2 * 4)
x = (-10 ± √(100 - 576)) / 8
x = (-10 ± √(-476)) / 8
Since the discriminant is negative, the equation has no real solutions. Therefore, there are no critical points for the given function.
Hence, the critical points are ∅ (empty set).
To learn more about critical value click :
https://brainly.com/question/31129453
#SPJ4
Round 684 to the nearest hundred

Answers
Answer:
700
Step-by-step explanation:
Examples of distribution
Answers
Answer:
see below
Step-by-step explanation:
5(2a+2b+2c)
you must distribute the 5 among the values in parenthesis
4(x-3)
you must distribute the 4 among the values in parenthesis
Hope this helps! :)
What’s the probability?

Answers
Answer:
sorry I don't know
Step-by-step explanation:
OK
OK jsjzjxjxndzkxk
s
PLZ MARK ME AD BRAINLIST
Thirty-five samples of size 7 each were taken from a fertilizer-bag-filling machine at Panos Kouvelis Lifelong Lawn Ltd. The results were: Overall mean =60.75lb.; Average range R ˉ =1.78lb. a) For the given sample size, the control limits for 3-sigma x ˉ chart are: Upper Control Limit (UCL x ˉ )= lb. (round your response to three decimal places). Lower Control Limit (LCL x ˉ )= Ib. (round your response to three decimal places). b) The control limits for the 3-sigma R-chart are: Upper Control Limit (UCL R )= Ib. (round your response to three decimal places).
Answers
a. The control limits for the 3-sigma x-bar chart are: UCL x-bar = 61.744 lb. and LCL x-bar = 59.756 lb.
b. The control limit for the 3-sigma R-chart is UCL R = 4.051 lb., rounded to three decimal places.
(a) To determine the control limits for the 3-sigma x-bar chart, we need to use the given information of the sample size, overall mean, and average range.
For the x-bar chart, the control limits are calculated using the formula:
Upper Control Limit (UCL x-bar) = overall mean + (A2 * average range)
Lower Control Limit (LCL x-bar) = overall mean - (A2 * average range)
Where A2 is a constant depending on the sample size. For a sample size of 7, the value of A2 is 0.577.
Substituting the values into the formula, we get:
Upper Control Limit (UCL x-bar) = 60.75 + (0.577 * 1.78) = 61.744
Lower Control Limit (LCL x-bar) = 60.75 - (0.577 * 1.78) = 59.756
Therefore, the control limits for the 3-sigma x-bar chart are: UCL x-bar = 61.744 lb. and LCL x-bar = 59.756 lb.
(b) To calculate the control limits for the 3-sigma R-chart, we only need the value of the average range.
The control limits for the R-chart are calculated as follows:
Upper Control Limit (UCL R) = D4 * average range
Lower Control Limit (LCL R) = D3 * average range
For a sample size of 7, the values of D3 and D4 are 0 and 2.282, respectively.
Substituting the values into the formula, we get:
Upper Control Limit (UCL R) = 2.282 * 1.78 = 4.051 lb.
Therefore, the control limit for the 3-sigma R-chart is UCL R = 4.051 lb., rounded to three decimal places.
Learn more about x-bar chart here:
brainly.com/question/31861365
#SPJ11
at a rehearsal dinner the night before a wedding, the bride and groom need to assign 10 people to two tables of five people. how many different groups of five can they form?
Answers
The bride and groom can form 252 different groups of five people from the total of 10 people at the rehearsal dinner, as they need to assign them to two tables of five people each.
To determine the number of different groups of five people that can be formed, we can use the concept of combinations. In this scenario, we have 10 people who need to be divided into two groups of five people each.
The number of ways to choose five people out of 10 can be calculated using the combination formula. The formula for combinations is given by:
C(n, r) = n! / (r! * (n - r)!)
Where n represents the total number of people and r represents the number of people to be chosen. In this case, n = 10 and r = 5.
Plugging these values into the formula, we get:
C(10, 5) = 10! / (5! * (10 - 5)!)
= (10 * 9 * 8 * 7 * 6 * 5!) / (5! * 5 * 4 * 3 * 2 * 1)
= (10 * 9 * 8 * 7 * 6) / (5 * 4 * 3 * 2 * 1)
= 252
Therefore, the bride and groom can form 252 different groups of five people from the total of 10 people at the rehearsal dinner. This means that there are 252 distinct ways to divide the 10 people into two tables of five people each, providing flexibility in creating diverse groups for the dinner.
Learn more about divide here:
https://brainly.com/question/15381501
#SPJ11
What are binary integer variables?
a. Variables with any two values, a and b.
b. Variables with values 0 and 1.
c. Variables whose sum of digits is 2.
d. Variables with values between 0 and 1.
Answers
Binary integer variables are variables whose values consist of two values, 0 and 1.
Correct answer will be :- b. Variables with values 0 and 1.
These values are also known as bits, which are represented as 0 and 1 in computers. Binary integer variables are used in computing as a way to represent numbers, characters, and instructions. Binary integer variables are used to represent information in digital systems, because they can be used to represent any value with a single bit.
For example, a single bit can represent a number, letter, or instruction. Binary integer variables are also used in computer programming, as they can be used to represent boolean values, such as true and false. Additionally, they can be used to represent various types of data, such as numbers, characters, and images.
know more about integer variables here
https://brainly.com/question/27855584#
#SPJ11
A science test, which is worth 100 points, consists of 24 questions. Each question is worth either 3 points or 5 points. If x is the number of 3-point questions and y is the number of 5-point questions, the system shown represents this situation. x + y = 24 3x + 5y = 100 What does the solution of this system indicate about the questions on the test? The test contains 4 three-point questions and 20 five-point questions. The test contains 10 three-point questions and 14 five-point questions. The test contains 14 three-point questions and 10 five-point questions. The test contains 20 three-point questions and 8 five-point questions.
Answers
Answer:
The test has 10 3-point questions and 14 5-point questions.
Step-by-step explanation:
x + y = 24
3x + 5y = 100
From the first equation:
3x + 3y = 72
Subtracting:
3x - 3x + 5y - 3y = 100 -72
2y = 28
so y = 14
x + 14 = 24 so x = 10.
10*3 + 5*14
= 30 + 70 = 100 points.
Let
\(\boxed{\sf f(x)=\begin{cases}\sf \dfrac{kcosx}{\pi -2x},x\neq \dfrac{\pi}{2} \\ \sf 3,x=\dfrac{\pi}{2}\end{cases}}\)
If
\(\\ \rm\hookrightarrow {\displaystyle{\lim_{x\to \dfrac{\pi}{2}}}}f(x)=f\left(\dfrac{\pi}{2}\right)\)
Find k
Note:-
Spams will be deleted on the spot.
Answer with proper explanation
Answers
Answer is in attachment.
k=6
![Let [tex]\boxed{\sf f(x)=\begin{cases}\sf \dfrac{kcosx}{\pi -2x},x\neq \dfrac{\pi}{2} \\ \sf 3,x=\dfrac{\pi}{2}\end{cases}}[/tex]If](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/LP4ozS0QUikvXPZzynx6dOftZjqc6bYv.jpeg)
We are provided with ;
\({:\implies \quad \bf f(x)=\displaystyle \begin{cases}\bf \dfrac{k\cos (x)}{\pi -2x}\:\:,\:\: x\neq \dfrac{\pi}{2}\\ \\ \bf 3\:\:,\:\: x=\dfrac{\pi}{2}\end{cases}}\)
Also we are given with ;
\({:\implies \quad \displaystyle \bf \lim_{x\to \footnotesize \dfrac{\pi}{2}}f(x)=f\left(\dfrac{\pi}{2}\right)}\)
At first , let's define the function at x = π/2 . Now , as given that f(x) = 3 , x = π/2. Implies , f(π/2) = 3
Now , we have ;
\({:\implies \quad \displaystyle \sf \lim_{x\to \footnotesize \dfrac{\pi}{2}}f(x)=3}\)
Now , As in RHS , x is approaching π/2 , means that x is in neighbourhood of π/2 , x is coming towards π/2 , but it's not π/2 , implies f(x) for the limit in LHS is defined for x ≠ π/2 or we don't have to take value of x as π/2 , means x ≠ π/2 in that case , means we have to take f(x) = {kcos(x)}/π-2x , x ≠ π/2 for the limit given in LHS ,
\({:\implies \quad \displaystyle \sf \lim_{x\to \footnotesize \dfrac{\pi}{2}}\dfrac{k\cos (x)}{\pi -2x}=3}\)
Now , As k is constant , so take it out of the limit
\({:\implies \quad \displaystyle \sf k \lim_{x\to \footnotesize \dfrac{\pi}{2}}\dfrac{\cos (x)}{\pi -2x}=3}\)
For , further evaluation of the limit , we will use substitution , putting ;
\({:\implies \quad \sf x=\dfrac{\pi}{2}-y\:\: , as\:\: x\to \dfrac{\pi}{2}\:\:,\: So\:\: y\to0}\)
Putting ;
\({:\implies \quad \displaystyle \sf k \lim_{y\to0}\dfrac{\cos \left(\dfrac{\pi}{2}-y\right)}{\pi -2\left(\dfrac{\pi}{2}-y\right)}=3}\)
Now , we knows that
\({\boxed{\bf{\cos \left(\dfrac{\pi}{2}-\theta \right)=\sin (\theta)}}}\)Using this , we have :
\({:\implies \quad \displaystyle \sf k \lim_{y\to0}\dfrac{\sin (y)}{\pi -\bigg\{2\left(\dfrac{\pi}{2}\right)-2y\bigg\}}=3}\)
\({:\implies \quad \displaystyle \sf k \lim_{y\to0}\dfrac{\sin (y)}{\pi -(\pi -2y)}=3}\)
\({:\implies \quad \displaystyle \sf k \lim_{y\to0}\dfrac{\sin (y)}{\cancel{\pi}-\cancel{\pi} +2y}=3}\)
\({:\implies \quad \displaystyle \sf k \lim_{y\to0}\dfrac{\sin (y)}{2y}=3}\)
Take ½ out of the limit as it's too constant ;
\({:\implies \quad \displaystyle \sf \dfrac{k}{2} \lim_{y\to0}\dfrac{\sin (y)}{y}=3}\)
Now , we also knows that ;
\({\boxed{\displaystyle \bf \lim_{h\to0}\dfrac{\sin (h)}{h}=1}}\)Using this we have ;
\({:\implies \quad \sf \dfrac{k}{2}=3}\)
\({:\implies \quad \bf \therefore \quad \underline{\underline{k=6}}}\)
help me plzzzzzzzzzzzz

Answers
Answer:
The answer to the question provided is 45.
Step-by-step explanation:
You add by ten.
The amount of time I seen this question-
Please Help 100 POINTS!!!

Answers
Answer:
B
Step-by-step explanation:
Answer:
B. \(\frac{x^2}{3^2} +\frac{y^3}{2^2} =1\)
Step-by-step explanation:

5-3x=10
I’m sorry I know it’s easy but I’m not getting the answer, it kinda confuses me
Answers
Answer:
x= -5/3
Step-by-step explanation:
(you dont have to apologize for not knowing something <3)
Subtract the numbers
Divide both sides of the equation by -3
Answer: x = - 5 / 3
Hope it helps ! Stay safe : )
Can u mark me brainlies
If u want but here is ur answer
find the value of y when x equals -1.
8x - 2y =10
Answers
Answer:
y = - 9
Step-by-step explanation:
Substitute in -1 for x
8(-1) - 2y = 10
-8 - 2y = 10
Subtract -8 from both sides
-8 - (-8) cancels out to 0
10 - (-8) = 18
We are left with:
-2y = 18
Divide by -2 on both sides.
-2y/-2 = y
18/-2 = -9
y = -9
sarah is playing a game in which she rolls a number cube 20 times the results are recorded in the chart below. what is the experimental probability of rolling a 1 or a 2? answers 0.3, 0.45, 0.65, 1.25.
Answers
The experimental probability of rolling a 1 or a 2 is 0.2.
Hence, Option A is correct.
We know that,
The experimental probability of an event is defined as the number of times the event occurred divided by the total number of trials.
In this case,
The event is rolling a 1 or a 3,
Which occurred ⇒ 3 + 1
= 4 times.
Given that there are total number of trials = 20.
Therefore,
The experimental probability of rolling a 1 or a 3 = 4/20,
= 1/5
= 0.2
Hence, the required probability is 0.2.
Learn more about the probability visit:
https://brainly.com/question/13604758
#SPJ1
The complete question is:
Sarah is playing a game in which she rolls a number cube 20 times. The results are recorded in the chart below. What is the experimental probability of rolling a 1 or a 3?
Number on cube:1,2,3,4,5,6
Number of times event occurs:3,6,1,5,3,2
A.0.2
B.0.3
C.0.6
D.0.83
this is 6th grade math not no 2309422347324782344872e+ - 1232434534532421e+ collage math

Answers
Answer:
4 1/2
Step-by-step explanation:
Answer:
The answer is 90/20
Step-by-step explanation:
3 3/4:
3x4=12+3=15/4
Find out 5/6 reciprocal (Just turn it around)
6/5
Then your left with 15/4 x 6/5 (psssst You have to change the division symbol to multiplication!!)
15/4 x 6/5= 90/20
pLEASE HELP me this is due today and dont post links plz?

Answers
Answer:
35
Step-by-step explanation:
Add them together and then divide
Answer:
b + b + h + h
Step-by-step explanation:
You are finding the perimeter of the given rectangle. Note that by definition of a rectangle, the opposite parallel sides will have the same measurement. In this case, Terrance gives the expression of 2b + 2h, and so simply just expand the expression:
2b + 2h = b + b + h + h
~
Emily earns $15 for each car she washes. Create an equation to represent the relationship between the number of cars washed,c, and the amount, in dollars, Emily earns, m.
Answers
Answer:
15c = m
Step-by-step explanation:
for every car she washes she learns 15 dollars. So you would multiply the number of cars she washes by 15 to get the amount she earns
Solve 7x − 2(x + 1) = 6x + 14. (5 points)
−12
12
−16
16
Answers
Answer:
C
X=-16
Step-by-step explanation:
Someone please help i can’t find the answer.

Answers
Answer:
f(3) = 4
Step-by-step explanation:
Give x = 3 in the interval x ≥ 1 then f(x) = x + 1 , and
f(3) = 3 + 1 = 4
