Solve for k.
k/4 + 3 = 14
k =
Answers
Answer:
The answer is k = 44.
Step-by-step explanation:
1) Subtract 3 from both sides.
\( \frac{k}{4} = 14 - 3\)
2) Simplify 14 - 3 to 11.
\( \frac{k}{4} = 11\)
3) Multiply both sides by 4.
\(k = 11 \times 4\)
4) Simplify 11 × 4 to 44.
\(k = 44\)
Therefor, the answer is k = 44.
Answer:
k = 44
Step-by-step explanation:
Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation :
k/4 + 3 - (14) = 0
k
Simplify —
4
k
(— + 3) - 14 = 0
4
Adding a whole to a fraction
Rewrite the whole as a fraction using 4 as the denominator :
3 3 • 4
3 = — = —————
1 4
Equivalent fraction: The fraction thus generated looks different but has the same value as the whole
Common denominator: The equivalent fraction and the other fraction involved in the calculation share the same denominator
Adding up the two equivalent fractions
Add the two equivalent fractions which now have a common denominator
Combine the numerators together, put the sum or difference over the common denominator then reduce to lowest terms if possible:
k + 3 • 4 k + 12
————————— = ——————
4 4
(k + 12)
———————— - 14 = 0
4
Subtracting a whole from a fraction
Rewrite the whole as a fraction using 4 as the denominator :
14 14 • 4
14 = —— = ——————
1 4
Adding up the two equivalent fractions
(k + 12) - (14 • 4) k - 44
—————————— = ——————
4 4
k - 44
—————— = 0
4
Where a fraction equals zero, its numerator, the part which is above the fraction line, must equal zero.
Now, to get rid of the denominator, Tiger multiplys both sides of the equation by the denominator.
Here's how:
k - 44
———— • 4 = 0 • 4
4
Now, on the left hand side, the 4 cancels out the denominator, while, on the right hand side, zero times anything is still zero.
The equation now takes the shape :
k - 44 = 0
Solve : k - 44 = 0
Add 44 to both sides of the equation :
k = 44
Related Questions
Candice is playing an online trivia game. She has 75 points and earns 3 points for each correct answer. She will advance to the next round if her score is over 90 points which statement best describes how antibiotics are used?
75x + 3 > 90
3x + 90 90
3x + 75 < 90
Answers
Answer:
3x+75>90
Step-by-step explanation:
P.S Can I have brainliest?
Answer:
3x + 75 < 90
Step-by-step explanation:
Can i be brainlist i work very hard
Please help me y’all!!

Answers
Answer:
d
Step-by-step explanation:
hope this helps
Moses and Louis ran laps after school to train for the basketball team. The ratio of the number of laps Moses ran to the number of laps Louis ran was two to three.
If Moses ran 8 laps, how many laps did Louis run?
Answers
Step-by-step explanation: the ratio was two to three Moses ran 8 laps meaning 2 multiplied by 4 now you multiply 3 times 4 to get your answer
find the measure of one interior angle in each polygon. Round your answer to the nearest tenth if Necessary.

Answers
An interior angle of a polygon is an angle formed inside the two adjacent sides. In our case, an interior angle is the angle in red color:
In our case, there are 8 sides so our polygon is an octagon. So, the size of each interio angle is given by
\(\frac{(8-2)\times180}{8}=\frac{6\times180}{8}=135\)Therefore, the answer is 135 degrees:


The function f:[−2,1]→[0,2];f(x)=∣x∣ is surjective but not injective injective but not surjective not well defined bijective
Answers
It is not surjective because there is no element in the range that maps to the value 2. The absolute value function only takes non-negative values, so the range is limited to [0, 2), excluding 2.
The function f(x) = |x|, defined on the interval [-2, 1] with the range [0, 2], is injective but not surjective.
To show that it is injective, we need to demonstrate that distinct elements in the domain map to distinct elements in the range. Since the absolute value function |x| always returns a non-negative value, any negative value in the domain will be mapped to its positive counterpart in the range. For example, f(-2) = |-2| = 2 and f(1) = |1| = 1. Thus, distinct elements in the domain have distinct images in the range, establishing injectivity.
However, It is not surjective because there is no element in the range that maps to the value 2. The absolute value function only takes non-negative values, so the range is limited to [0, 2), excluding 2.
Learn more about surjective here:
https://brainly.com/question/19516776
#SPJ11
This year (2022), Evan graduated from college and took a job as a deliveryman in the city. Evan was paid a salary of $73,650 and he received $700 in hourly pay for part-time work over the weekends. Evan summarized his expenses as follows:
Cost of moving his possessions to the city (125 miles away) $ 1,200
Interest paid on accumulated student loans 2,890
Cost of purchasing a delivery uniform 1,490
Cash contribution to State University deliveryman program 1,345
Calculate Evan's AGI and taxable income if he files single. Assume that interest payments were initially required on Evan's student loans this year.
Answers
To calculate Evan's AGI (Adjusted Gross Income) and taxable income if he files as a single taxpayer, we need to consider his income and deductible expenses.
Calculate Evan's total income:
- Salary: $73,650
- Part-time hourly pay: $700
Total income = Salary + Part-time pay = $73,650 + $700 = $74,350
Deductible expenses:
- Moving expenses: $1,200
- Student loan interest: $2,890
- Uniform cost: $1,490
- Cash contribution: $1,345
Total deductible expenses = $1,200 + $2,890 + $1,490 + $1,345 = $6,925
Calculate AGI:
AGI = Total income - Total deductible expenses
AGI = $74,350 - $6,925 = $67,425
Evan's taxable income is equal to his AGI since there were no other deductions mentioned in the question.
Therefore, Evan's AGI is $67,425, and his taxable income is also $67,425.
To know more about income , visit ;
https://brainly.in/question/15692103
#SPJ11
Evan's AGI is $67,425 and his taxable income is $54,875 if he files as a single taxpayer.
We have,
Income:
Salary: $73,650
Part-time work pay: $700
Total income: $73,650 + $700 = $74,350
Deductible Expenses:
Cost of moving possessions: $1,200
(This deduction applies if the move meets certain distance and time requirements. Since the move was 125 miles away, it meets the distance requirement.)
Interest paid on student loans: $2,890
Cost of purchasing a delivery uniform: $1,490
Cash contribution to State University deliveryman program: $1,345
Total deductible expenses:
$1,200 + $2,890 + $1,490 + $1,345
= $6,925
Now we can calculate Evan's AGI and taxable income:
AGI (Adjusted Gross Income)
= Total income - Deductible expenses
AGI = $74,350 - $6,925 = $67,425
Taxable Income = AGI - Standard Deduction
For a single filer in 2022, the standard deduction is $12,550.
Taxable Income = $67,425 - $12,550 = $54,875
Therefore,
Evan's AGI is $67,425 and his taxable income is $54,875 if he files as a single taxpayer.
Learn more about expressions here:
https://brainly.com/question/3118662
#SPJ4
PLEASE ANSWER!!!! BAD THINGS WILL HAPPEN IF I FAIL THIS TEST





Answers
Answer:
2 8 20
Step-by-step explanation:
sorry if my answer is wrong
Given that y varies indirectly as x and that x = 15 when y = 3, then the value of k is
Answers
Answer:
Step-by-step explanation:
the equation of this function has the form y = k/x, and when x = 15 and y = 3, the value of k can be calculated as follows:
3 = k/15, or (by multiplying both sides by 15) k = 45
Then y = 45/x
EOQ Model
Suppose during your college life, every year you need $5,000 cash to spend in addition to the studying expenses. Each time in need of cash, you decide to go to the bank for that. And the transportation costs you $5 (assumed amount) of going to the bank and coming back. Assume that the current saving/checking link account has an interest rate of 5%. Please find the optimal solution of the amount of cash each time for the withdraw.
Answers
The optimal solution for the amount of cash to withdraw each time to minimize transportation costs and maximize interest earnings is determined by calculating the Economic Order Quantity (EOQ) using the formula Q = √((2 * C * T) / r), and rounding the result to a convenient amount.
The Economic Order Quantity (EOQ) model is typically used for inventory management, not for optimizing cash withdrawals. However, if we assume that the question is seeking an optimal withdrawal strategy to minimize transportation costs and maximize interest earnings, we can approach it as follows:
Let's denote:
C = Annual cash need ($5,000)
T = Transportation cost per visit ($5)
r = Annual interest rate (5%)
To find the optimal solution for the amount of cash to withdraw each time, we can consider the trade-off between transportation costs and interest earnings. The objective is to minimize the total cost.
Calculate the optimal order quantity (Q) using the EOQ formula:
Q = √((2 * C * T) / r)
Round the calculated Q to the nearest convenient amount, such as multiples of $100 or $500.
The optimal solution would be to withdraw the rounded Q amount each time to minimize transportation costs while still meeting the annual cash need.
To know more about optimal solution,
https://brainly.com/question/31964994
#SPJ11
(-15)(-4) help meeee
Answers
Answer:
+60
Step-by-step explanation:
This is the answer because you multiply -15 x -4 =60
because negative and negative make positive and =60
Hope this helps:)
pls mark brainly
how do i sketch the graph for these inequalities?
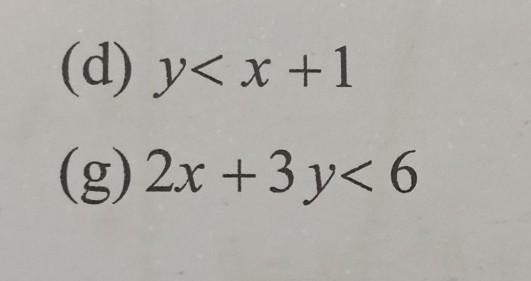
Answers
Step by step on how to solve and graph with attached graph
I like to solve and graph using standard form and substituting 0 for x to find y and 0 for y to find x
(d) y< x + 1 in standard form is -x + y < 1
(0) + y < 1
Simplify
y < 1
-x + (0) < 1
Simplify
-x < 1
x < -1
(-1, 0) and ( 0, 1) dashed line shaded below ( less than) the line
Your solution where the graphs intersect is
( .6 ,
(g) 2x + 3y < 6
2(0) + 3y < 6
3y < 6
Divide both sides by 3
3/3y < 6/3
y < 3
2x + 3(0) < 6
2x < 6
Divide both sides by 2
2/2x < 6/2
x < 3
(3, 0 ) and ( 0, 3) dashed line shaded below ( less than) the line
Your solution where the lines intersect
( .6 , 1.6 ) the graph is attached

identify the surface whose equation is given. rho2(sin2(φ) sin2(θ) + cos2(φ)) = 16
Answers
The equation provided is: ρ²(sin²(φ)sin²(θ) + cos²(φ)) = 16, This equation is in spherical coordinates,
where ρ represents the radial distance from the origin, φ is the polar angle (or the angle between the positive z-axis and the vector), and θ is the azimuthal angle (or the angle between the positive x-axis and the projection of the vector onto the xy-plane).
Now, let's analyze the equation further: 1. Divide both sides of the equation by 16 to isolate ρ²: ρ² = 16 / (sin²(φ)sin²(θ) + cos²(φ)) 2. Take the square root of both sides to find ρ: ρ = √(16 / (sin²(φ)sin²(θ) + cos²(φ))).
From this, we can see that the surface is defined by the radial distance ρ, which depends on the angles φ and θ. This indicates that the given equation represents a 3-dimensional surface in spherical coordinates.
To know more about equation click here
brainly.com/question/649785
#SPJ11
A customer bought a soda and 2 hotdogs for $7 another customer bought a soda in for hotdogs for $12
Answers
There are 3 ¼ packages of pencils on the desk. One full package weighs 1 ½ pounds. How much do all the containers weigh?
Answers
Answer and Explanation
\(4\ \frac{3}{4}\) \(or\) \(\frac{19}{4}\) = \(4.75\)
__________________________________________________________
We can prove this is correct by adding and multiplying some of the fractions.
\(\frac{1}{2}\cdot\frac{2}{2}\) = \(\frac{2}{4}\)
There.
__________________________________________________________
Now, we will add the fractions.
\(\frac{1}{4}+\frac{2}{4}\) = \(\frac{3}{4}\)
\(3+1\) = \(4\)
\(4+\frac{3}{4}\) = \(4\ \frac{3}{4}\)
__________________________________________________________
So, the answer is \(4\ \frac{3}{4}\).
__________________________________________________________
Hope this helps! <3
__________________________________________________________
Lexi runs a race at school. She runs at a rate of 4 miles per hour for the first mile, then increases her rate to 5 miles per hour until the last mile when she runs 6 miles per hour. Which equation below represents her time, T. In hours, If she runs a total of x miles
Answers
Answer:
60T = 12x - 1
Step-by-step explanation:
In speed distance and time, time(t) is given by
time = distance(d)/speed(s)
total distance ran = x miles
case 1
d = 1 mile
speed = 4 miles per hour
as time = distance(d)/speed(s)
t = 1/4
____________________________
case 2
speed = 5 miles per hour
it is given that out of x miles for first mile and last mile her speed was 5 miles per hour
thus distance for this speed can be calculated by
subtracting first and last mile from x miles
therefore
distance = x-2 miles\
t = (x-2)/5
_____________________________________
case 3
distance = 1 mile
speed = 6 miles per hour
t = 1/6
______________________________
Total time T as required will be sum of time for the 3 case calculated above
T = 1/4 + (x-2)/5 + 1/6
T = 1/4 + (x - 2)/5 + 1/6 (taking LCM of 6,5,4 as 60 and solving)
T = (15 + 12x - 24 + 10)/60
T = (12x - 1)/60
60T = 12x - 1
Thus, equation 60T = 12x - 1 represents her time T
kamau toured switerland from germany. in switzerland he bought his wife a present worth 72deutsche marks.find the value of present in .k
[a] swiss francs
[b] ksh correct to the nearest sh, if
1 swiss franc =1.25 deutsche marks.
1 swiss franc=48.2 ksh
Answers
The value of the present in Kenyan shillings is approximately 2773.12 ksh.
We can convert the value 72 Deutsche marks into Swiss francs as follows:
72 Deutsche marks × (1 Swiss franc / 1.25 Deutsche marks)
= 57.6 Swiss francs
Then, we can convert Swiss francs into Kenyan shillings as follows:
57.6 Swiss francs × (48.2 ksh / 1 Swiss franc)
= 2773.12 ksh
Therefore, the value of the present in Kenyan shillings is approximately 2773.12 ksh
To learn more on Unit of Measurement click:
https://brainly.com/question/15402847
#SPJ1
Given (x^2-a)(3x-2)=3x^3+bx^2+cx+10, find values for a b and c.

Answers
The values of the constants for the given quadratic equation are a=2, b=3, and c=7.
What is a quadratic equation?The values of the constants for the given quadratic equation are a=2, b=3, and c=7.
The quadratic equation is defined as a polynomial with a degree of two or with a maximum power of a variable in a polynomial of 2, which will cut two intercepts on the graph at the x-axis.
Here is an equation to consider:
2x²+3x+7 = 0
Using the general equation as a comparison to the previous equation:
ax²+bx+c = 0
Thus, the constants' values will be as follows:
a=2, b=3 c=7
Therefore, for the following quadratic equation, the values of the constants are a=2, b=3, and c=7.
The values of the constants for the given quadratic equation are a=2, b=3, and c=7.
To learn more about quadratic equation refer
https://brainly.com/question/4600943
#SPJ1
A blue die and a red die are thrown. B is the event that the blue comes up an odd number. E is the event that both dice come up odd.
Enter the sizes of the sets |E ∩ B| and |B|
Answers
The size of the set |E ∩ B| is 2, and the size of the set |B| is 3.
There are six possible outcomes when two dice are thrown:
{(1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3), (4,1), (4,2), (4,3), (5,1), (5,2), (5,3), (6,1), (6,2), (6,3)}.
Out of these 18 outcomes, the following three satisfy the event E (both dice are odd): (1,3), (3,1), and (3,3).
The following outcomes satisfy event B (the blue die is odd): (1,1), (1,3), (2,1), (2,3), (3,1), and (3,3).
Therefore, the size of the set |E ∩ B| is 2 (the two outcomes that satisfy both events are (1,3) and (3,1)), and the size of the set |B| is 3 (three outcomes satisfy the event B).
To learn more about Sets, visit:
https://brainly.com/question/25005086
#SPJ11
Which resources provides an opportunity to evaluate your readiness for a major assessment?
A. Reflection
B. Teacher tutorial
C. Illustrated glossary
D. Virtual Geoboard
Answers
What is 95/18 as a decimal?
Please include an explanation and the correct answer!
I will give brainliest to the best answer!
I need it in the next 5 mins!
Thank you!
Answers
Answer:
5.27777777
repeating 7s forever
rounded to 2 decimal places is:. 5.28
Hey there!
In order for you to find the decimal form of a fraction, you have DIVIDE the NUMERATOR (the TOP number) from the DENOMINATOR (the BOTTOM number)
Here’s the formula
a/b = a ÷ b = [decimal form]
ANSWERING YOUR QUESTION
95/18
= 95 ÷ 18
= 5.277778 ≈ 5.3 or 5.28
Therefore, your answer is: 5.277778
Good luck on your assignment and enjoy your day!
~Amphitrite1040:)
Amelia, Luis, Shauna, and Clarence used different approaches to solve the inequality
7.2b + 6.5 > 4.8b – 8.1.
Amelia started by subtracting 7.2b from both sides to get 6.5 > –2.4b – 8.1.
Luis started by subtracting 4.8b from both sides to get 2.4b + 6.5 < – 8.1.
Shauna started by subtracting 6.5 from both sides to get 7.2b > 4.8b – 14.6.
Clarence started by adding 8.1 to both sides to get 7.2b + 14.6 > 4.8b.
Which student’s first step was incorrect, and why?
Answers
Answer:
B
Step-by-step explanation:
Luis started by subtracting 4.8b from both sides to get 2.4b + 6.5 < – 8.1.
Answer:
Luis’s, because he flipped the inequality sign when he subtracted
Step-by-step explanation:
Luis’s, because he flipped the inequality sign when he subtracted
Solve for x Enter the solutions from least to greatest 5x^2 + 45x + 90 = 0

Answers
I’m pretty sure the lesser X is -6 and the greater X is -3
2. A town is planning a circular walkway that will be 2 meters wide. The walkway will have an inter radius of 5 meters with a circumference of about 31. 4 meters. Find the area of the wallway
Answers
The area of the walkway is 24π square meters.
To find the area of the walkway, we need to subtract the area of the inner circle from the area of the outer circle.
The inner circle has a radius of 5 meters, so its area can be calculated using the formula for the area of a circle: A_inner = π * \((r_inner)^{2}\).
A_inner = π * \(5^{2}\) = 25π square meters.
The outer circle has a radius equal to the sum of the inner radius and the width of the walkway. In this case, the outer radius is 5 + 2 = 7 meters.
The area of the outer circle can be calculated in the same way: A_outer = π * \((r_outer)^{2}\).
A_outer = π * \(7^{2}\) = 49π square meters.
Now, we can find the area of the walkway by subtracting the area of the inner circle from the area of the outer circle: A_walkway = A_outer - A_inner.
A_walkway = 49π - 25π = 24π square meters.
The area of the walkway is 24π square meters, where π (pi) is a mathematical constant approximately equal to 3.14159.
To learn more about area here:
https://brainly.com/question/32312055
#SPJ4
y= -(x+3)^2 -5
What is the leading coefficient?
How do you find the vertex?
Answers
Answer:
To find the leading coefficient, first expand the function:
\(y= -(x+3)^{2} -5\\\\y=-(x^{2} +6x+9)-5\\\\y=-x^{2} -6x-9-5\\\\y=-x^{2} -6x-14\)
The leading coefficient is the coefficient of the highest-order term, which, in this case, would be the -1 from -x².
To find the vertex: see image below
Vertex = (-3, -5)

Three ballet dancers are positioned on stage. Oliver Is 6.3 feet straight behind Dana and 6.3
feet directly left of Ashley. When the music begins, Oliver twirls to Ashley's position, then
leaps to Dana's position, and finally walks back to his original position. How far did Oliver
travel? If necessary, round to the nearest tenth.
Answers
Oliver travelled the distance of 21.5 ft
What is perimeter?
The complete length of a shape's edge serves as its perimeter in geometric terms. Adding the lengths of all the sides and edges that surround a form yields its perimeter. It is calculated using linear length units such centimeters, meters, inches, and feet.
As shown in the figure, we need to find the perimeter of the triangle ABC.
Perimeter = g + h +f ............(1)
g=f = 6.3 ft
Finding h using pythogoras theorem formula:
h² = g² + f²
= 6.3² + 6.3²
= 79.38
h =√79.38 = 8.909 ≈ 8.9 ft
So, (1) => Perimeter = 6.3 + 6.3 + 8.9 = 21.5 ft
Thus, Oliver travelled the distance of 21.5 ft
To learn more about the perimeter form the link:
https://brainly.com/question/19819849
#SPJ1

Need help pleaseeeeeeee

Answers
The volume of the right square pyramid with the dimensions e = 5m, h = 4m, and s = 6m is 48m³.
What is pyramid?Pyramid is a structure with a polygonal base and triangular sides that meet at a point. Pyramids have been used throughout history as tombs, temples and monuments. Many of the most famous pyramids are located in Egypt, such as the Great Pyramid of Giza.
The volume of a right square pyramid is equal to one-third of the base area multiplied by the height. To find the volume of this pyramid, we first need to calculate the base area.
The base area of a square pyramid is equal to the length of one side (s) squared. Since the length of one side of this pyramid is 6m, the base area is 6m x 6m, which equals 36m².
Now that we know the base area, we can calculate the volume of the pyramid. The volume is equal to one-third of the base area multiplied by the height. In this case, the volume of the pyramid is one-third of 36m² multiplied by 4m, which equals 48m³.
Therefore, the volume of the right square pyramid with the dimensions e = 5m, h = 4m, and s = 6m is 48m³.
To learn more about pyramid
https://brainly.com/question/218706
#SPJ1
Determine which of the following graphs does not represent a function

Answers
Explanation:
Assuming there are four answer choices, we can eliminate choices A through C because they are functions. This is because they pass the vertical line test.
The vertical line test is where we try to draw a single vertical line through more than one point on the curve. If such a task is possible, then it is said to "fail the vertical line test" and it's not a function.
For choice A, we cannot draw a single vertical line through more than one point on the parabola. Choice A passes the vertical line test. Hence, it is a function. The same goes for choices B and C.
Unfortunately choice D is not shown, but if it's the only thing left, then I'm assuming that it's some curve that fails the vertical line test.
A statistics student wants to determine if there is a relationship between a student's number of absences, x, and their
grade point average (GPA), y. The given data lists the number of absences and GPAs for 15 randomly selected
students.
Number of
Absences
GPA
15 1 0
9
12
3
3
2.1 4.3 4.5 3.2 4.0 1.7 3.8 2.9
6
1
3.6
2 7
3.4
2.6
Using technology, the y-intercept is
O4.5, which means a student with no absences has a GPA of 4.5.
O 4.5, which means a student with no absences is predicted to have a GPA of 4.5.
O 3.79, which means a student with no absences is predicted to have a GPA of 3.79.
O 3.79, but it does not make sense to interpret the y-intercept in this context.
0 4
3.1
2.8
9 10
2.8
4.1
Answers
Answer: The correct answer is:
The y-intercept is 3.79, which means a student with no absences is predicted to have a GPA of 3.79.
Explanation:
To determine the relationship between the number of absences and the GPA, the student can use linear regression analysis. The regression line can be obtained using software such as Excel or R. The y-intercept of the regression line represents the predicted value of the response variable (GPA) when the predictor variable (number of absences) is zero.
Using technology, the y-intercept for this data set is found to be 3.79. This means that a student with zero absences is predicted to have a GPA of 3.79. Therefore, the correct answer is that the y-intercept is 3.79 and it does make sense to interpret it in this context.
Step-by-step explanation:
A $0.25 \mathrm{~kg}$ stone is held $11 \mathrm{~m}$ above the top edge of a water well and then dropped in. The well has a depth of $7.3 \mathrm{~m}$. Taking $y=0$ at the top edge of the well, calculate
(a) the gravitational potential energy of the stone-Earth system before the stone is released
(b) the gravitational potential energy of the stone-Earth system after the stone reaches the bottom of the well
(c) the change in gravitational potential energy of the system from when the stone is released to when it reaches the bottom of the well.
Answers
The gravitational potential energy of the stone-Earth system can be calculated before the stone is released, after it reaches the bottom of the well, and the change in gravitational potential energy during the process.
Gravitational potential energy is given by the formula PE = mgh, where m is the mass of the object, g is the acceleration due to gravity, and h is the height.
(a) Before the stone is released, it is held 11 m above the top edge of the well. The mass of the stone is 0.25 kg, and the acceleration due to gravity is approximately 9.8 m/s². Using the formula, the gravitational potential energy is calculated as PE = (0.25 kg)(9.8 m/s²)(11 m).
(b) After the stone reaches the bottom of the well, its height is 7.3 m. Using the same formula, the gravitational potential energy at this point is given by PE = (0.25 kg)(9.8 m/s²)(7.3 m).
(c) The change in gravitational potential energy can be determined by subtracting the initial potential energy from the final potential energy. The change in gravitational potential energy is equal to the gravitational potential energy after reaching the bottom of the well minus the gravitational potential energy before the stone was released.
By calculating these values, we can determine the specific numerical values for (a), (b), and (c) based on the given data.
Learn more about gravitational here:
https://brainly.com/question/32609171
#SPJ11
The owners of a house that is assessed at $\$120,\!000$ pay $\$3,\!000$ in taxes. at the same rate, what is the tax, in dollars, for a house assessed at $\$160,\!000$?
Answers
According to the question The tax for a house assessed at $160,000 would be $4,000.
To find the tax for a house assessed at $160,000 using the same tax rate, we can set up a proportion based on the assessed values and taxes paid:
\(\(\frac{\text{{Assessed value of house 1}}}{\text{{Tax paid for house 1}}}\) = \(\frac{\text{{Assessed value of house 2}}}{\text{{Tax for house 2}}}\)\)
Substituting the given values, we have:
\(\(\frac{120,000}{3,000} = \frac{160,000}{x}\)\)
Cross-multiplying and solving for \(\(x\)\), we get:
\(\(x = \frac{160,000 \times 3,000}{120,000}\)\)
Calculating the expression on the right side, we find:
\(\(x = \$4,000\)\)
Therefore, the tax for a house assessed at $160,000 would be $4,000.
To know more about tax visit -
brainly.com/question/15089574
#SPJ11