Answers
Answer: 6
Step-by-step explanation:
\(f(12)=\frac{3(12)+6}{7}=\boxed{6}\)
Related Questions
Is there a value of r so that x=r, y=2, z=1 is a solution to thefollowing linear system? If so, find it
3x -2z= 4
x-4y+z= -5
-2x+3y+2z= 9
N.B. the large space in the first equation above is written as itis in the textbook.
Answers
No, x=r, y=2, z=1 is not solution to thefollowing linear system.
The question asks if there exists a value of r such that x=r, y=2, z=1 is a solution to the given system of linear equations. To find out, we can substitute these values into the equations and see if they are satisfied.
Starting with the first equation, 3x - 2z = 4:
Plugging in x=r, y=2, and z=1, we get:
3r - 2(1) = 4
Solving for r, we find that r = (4 + 2) / 3 = 2.
Next, we can substitute these values into the second equation, x - 4y + z = -5:
r - 4(2) + 1 = -5
Simplifying, we get:
r - 8 + 1 = -5
Subtracting 1 from both sides, we get:
r - 8 = -6
Adding 9 to both sides, we get:
r = 2
Finally, we can substitute these values into the third equation, -2x + 3y + 2z = 9:
-2r + 3(2) + 2(1) = 9
Solving for r, we get:
-2r + 6 + 2 = 9
Subtracting 2 from both sides, we get:
-2r = 1
Dividing both sides by -2, we get:
r = -0.5
Since r = 2 in two of the three equations and r = -0.5 in another, we conclude that there is no solution to the system with x = r, y = 2, and z = 1.
To know more about linear equations click on below link:
https://brainly.com/question/13738061#
#SPJ11
(-9) / *fill the blank* = 5
Answers
Answer:-1.8
Step-by-step explanation:
g the physical plant at the main campus of a large state university recieves daily requests to replace florecent lightbulbs. the distribution of the number of daily requests is bell-shaped and has a mean of 57 and a standard deviation of 8. using the empirical rule (as presented in the book), what is the approximate percentage of lightbulb replacement requests numbering between 57 and 73?
Answers
The approximate percentage of bulb replacement requests between 57 and 73 is 95%.
How do we calculate the approximate percentage?The empirical rule, also known as the 68-95-99.7 rule, is used to determine the percentage of observations that lie within a specified number of standard deviations of the means in a normal distribution. The rule states that approximately:
68% of the observations are within one standard deviation of the means
95% of the observations are within two standard deviations of the mean
99.7% of the observations are within three standard deviations of the mean
The given problem states that the distribution of the number of daily requests for fluorescent light bulbs at a university is bell-shaped and has a mean of 57 and a standard deviation of 8. Therefore, to find the approximate percentage of light bulb replacement requests between 57 and 73, we need to find the number of standard deviations of the means that are 73 and 57.
\(z-score = (x - \mu) / \sigma\)
Where
\(z-score\) is the number of standard deviations from the mean.\(x\) is the value of the observation\(\mu\) is the population mean\(\sigma\) is the population standard deviationFor x = 73,
\(z-score = (73 - 57) / 8\\z-score = 2\)
For x = 57,
\(z-score = (57 - 57) / 8\\z-score = 0\)
Therefore, observations 57 and 73 are separated by two standard deviations.
Using the empirical rule, we can say that approximately 95% of the observations lie within two standard deviations of the mean. Therefore, approximately 95% of the daily requests for replacement of fluorescent bulbs in the university are between 57 and 73.
Thus, the approximate percentage of bulb replacement requests between 57 and 73 is 95%.
See more information about normal distribution in: https://brainly.com/question/4079902
#SPJ11
The measure of angle FGH is 160°.
The measure of angle FGJ is 125°.
The measure of angle JGH is x°.
Find the value of x.
Answers
Answer:
160-125=45
I answered this before, I think you have a similar picture.
40) through: (-5, 2), slope
1
5
Answers
Answer:
y = 1/5x + 3
Step-by-step explanation:
y = mx + b
m: slope = 1/5
b: y - intercept
(x, y): (-5, 2)
2 = 1/5(-5) + b
2 = -1 + b
add 1 to both sides to get b alone
2 + 1 = -1 + b + 1
3 = b
i neeeed help quickkkk

Answers
Answer:
20 hours
Step-by-step explanation:
If your computer can download a movie in 5 hours, then it downloads \(\frac{1}{5}\) of a movie in 1 hour.
The extra processor in 1 hour, reduces the time down to 5 hours, so it downloads \(\frac{1}{4}\) of the movie in 1 hour.
The time that the extra processor will spend to download a whole movie added to \(\frac{1}{5}\) will equal \(\frac{1}{4}\) .
So our equation is \(\frac{1}{5} + \frac{1}{x} = \frac{1}{4}\).
To simplify this, lets multiply all sides by 20x.
\((\frac{1}{5}+\frac{1}{x} \cdot 20x) = \frac{1}{4}\cdot20x\\ 4x + 20 = 5x\)
Now we can simplify this equation.
\(20 = 5x-4x\\\\20 = x\\x = 20\)
So the extra processor alone would take 20 hours to download the movie.
Hope this helped!
Select the interval where the graph h is negative.

Answers
Answer: C
Step-by-step explanation:
Based on the graph, we know that it is negative if it is under the x-axis. It is also indicated by the negative labels.
A: incorrect
Looking at choice A, it says the interval is from -3<x<-2. This means we have to find x=-3 and x=-2. On the graph, that interval is above the x-axis, so it is positive, not negative.
B: incorrect
Looking at choice B, it says the interval is from 2<x<3. This means we have to find x=2 and x=3. On the graph, that interval is above the x-axis, so it is positive, not negative.
C: correct
Looking at choice C, it says the interval is from 4<x<5. This means we have to find x=4 and x=5. On the graph, that interval is under the x-axis, so it is negative.
Therefore, C is the correct answer.
A school has 2000 students a survey finds that 36 students out of a random sample of 80 student's are bilingual the margin of error for the survey is +4% find the interval in which the total number of bih Guam students is most likely to lie
Answers
Answer:
(820 ; 980)
Step-by-step explanation:
Given :
Sample size, n = 80
Number of bilingual from sample = 36
Sample proportion, phat = x / n = 36 / 80 = 0.45
Margin of Error = 4% = 0.04
Interval = sample proportion ± margin of error
0.45 ± 0.04
(0.41 ; 0.49)
(0.41 * 2000 ; 0.49 * 2000)
(820 ; 980)
What is the equation of the line, in standard form, connecting points (2, -3) and (4, 4)?
Responses
7x−2y−26=07 x minus 2 y minus 26 is equal to 0
7x+y−13=07 x plus y minus 13 is equal to 0
7x−2y−20=07 x minus 2 y minus 20 is equal to 0
2x−2y−7=02 x minus 2 y minus 7 is equal to 0
3x−y+10=0
Answers
Answer:
7x - 2y - 20 = 0
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
calculate m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (2, - 3 ) and (x₂, y₂ ) = (4, 4 )
m = \(\frac{4-(-3)}{4-2}\) = \(\frac{4+3}{2}\) = \(\frac{7}{2}\) , then
y = \(\frac{7}{2}\) x + c ← is the partial equation
to find c substitute either of the 2 points into the partial equation
using (4, 4 )
4 = \(\frac{7}{2}\) (4) + c = 14 + c ( subtract 14 from both sides )
- 10 = c
y = \(\frac{7}{2}\) x - 10 ← in slope- intercept form
multiply through by 2
2y = 7x - 20 ( subtract 2y from both sides )
0 = 7x - 2y - 20 , that is
7x - 2y - 20 = 0 ← required equation
Differentiate the expression x²y⁵ with respect to x. (use D for dy/dx).
Answers
To differentiate the expression x²y⁵ with respect to x, we need to use the product rule of differentiation.
The product rule states that the derivative of the product of two functions is equal to the first function times the derivative of the second function plus the second function times the derivative of the first function.
Using this rule, we can differentiate x²y⁵ as follows:
d/dx (x²y⁵) = 2xy⁵ + x²(5y⁴)(d/dx(x))
d/dx (x²y⁵) = 2xy⁵ + 5x²y⁴(d/dx(x))
We know that d/dx(x) = 1, so the final expression becomes:
d/dx (x²y⁵) = 2xy⁵ + 5x²y⁴
Therefore, the derivative of x²y⁵ with respect to x is 2xy⁵ + 5x²y⁴.
This expression represents the rate of change of x²y⁵ with respect to x. It tells us how much the value of x²y⁵ changes when we change x by a small amount. We have shown that the product rule is an essential tool in differentiating expressions, and we have used it to find the derivative of x²y⁵ with respect to x.
To know more about differentiation visit:
https://brainly.com/question/13958985
#SPJ11
Find the volume of a cylinder in cubic feet

Answers
Answer:
4398.23
Step-by-step explanation:
(2x-6)+4(x-3) I need help
Answers
Answer:
6x-18
x=-3
Step-by-step explanation:
2x - 6 + 4x - 12
6x - 18
The answer is 6x - 18.
Element x decays radioactively with a half life of 11 minutes. if there are 300 grams
of element x, how long, to the nearest tenth of a minute, would it take the element to
decay to 80 grams?
y= a(.5)
Answers
It Will take approximately 1.99 minutes for the element to decay to 80 grams.
To solve this problem, you can use the formula for exponential decay: y = a * b^x
Where "y" is the final amount of the substance, "a" is the initial amount of the substance, "b" is the decay constant (in this case, b = 0.5 since the half-life of element x is 11 minutes), and "x" is the time in which the decay occurs.
In this case, we are trying to find the value of "x" (the time in which the decay occurs) given the values of "y" (80 grams) and "a" (300 grams).
Substituting these values into the formula, we get:
80 = 300 * 0.5^x
To solve for x, we can divide both sides by 300 and take the logarithm of both sides: log(80/300) = log(0.5^x)
-1.386 = x * log(0.5)
-1.386 = x * -0.693
x = 1.99
This tells us that it would take approximately 1.99 minutes for the element to decay to 80 grams. Rounding to the nearest tenth of a minute, this is approximately 2.0 minutes.
Therefore, it would take approximately 1.99 minutes for the element to decay to 80 grams.
To learn more about Exponentials,
Visit; brainly.com/question/28596571
#SPJ4
The mean of 16, X, 3, 14,57 is 22. Find
Х
Answers
Answer:
20
Step-by-step explanation:
Given,
The mean of 16, X, 3, 14, 57 is 22.
Therefore,
(16+X+3+14+57)/5 = 22
(16+X+3+14+57) = 110
(90+X) = 110
X = 110-90
X = 20
The value of x will be 20.
What is an expression?
Mathematical expression is defined as the collection of the numbers variables and functions by using operations like addition, subtraction, multiplication, and division.
Given that;
The mean of set 16, X, 3, 14, 57 is 22.
Now,
Since, The mean of 16, X, 3, 14, 57 is 22.
Hence, By definition of mean we get;
⇒ 16 + X + 3 + 14 + 57 / 5 = 22
Solve for x as;
⇒ 90 + X / 5 = 22
⇒ 90 + X = 22 × 5
⇒ 90 + X = 110
⇒ X = 110 - 90
⇒ X = 20
Thus, The value of x will be 20.
Learn more about the mathematical expression visit:
brainly.com/question/1859113
#SPJ2
a scalar c is an eigenvalue of an n×n matrix a if the equation (a − ci) x = 0 has a non-trivial solution x. true or false?
Answers
Given statement 'A scalar c is an eigenvalue of an n×n matrix a if the equation (a − ci) x = 0 has a non-trivial solution x' is True.
In this question, we have been given a statement 'a scalar c is an eigenvalue of an n×n matrix a if the equation (a − ci) x = 0 has a non-trivial solution x. '
We need to decide whether the given statement is true or not.
By the definition of an eigenvalue of an n×n matrix A, a scalar c is an eigenvalue of an n×n matrix A if the equation (A − cI)x = 0 has a non-trivial solution x.
Thus given statement is True.
Therefore, a scalar c is an eigenvalue of an n×n matrix a if the equation (a − ci) x = 0 has a non-trivial solution x is True.
Learn more about the eigenvalue here:
https://brainly.com/question/16340865
#SPJ4
If f(x) = 2x ^ 2 + 3 and g(x) = x ^ 2 - 7 , find (f - g)(x) .
Answers
Answer:
x^2 + 10
Step-by-step explanation:
f(x) = 2x ^ 2 + 3
g(x) = x ^ 2 - 7
(f - g)(x) =2x ^ 2 + 3 - (x ^ 2 - 7 )
Distribute the minus sign
=2x ^ 2 + 3 - x ^ 2 + 7
Combine like terms
= x^2 + 10
rudy wanted to drive a car that uses less gasoline, so he bought a hybrid. there is a proportional relationship between the volume of gasoline rudy's car uses when driving on the highway (in gallons), x, and the distance he drives it on the highway (in miles), y. x (gallons) y (miles) 1 25 2 50 3 75 4 100 what is the constant of proportionality? write your answer as a whole number or decimal.
Answers
The constant of proportionality for x gallons water and y miles is k = 25
The ratio connecting two given numbers in what is known as a proportional relationship is the constant of proportionality.
Constant ratio, constant rate, unit rate, constant of variation, and even rate of change are other names for the constant of proportionality.
A proportionate connection is simple to represent as a straight line on a coordinate plane. It is a straight line because it is directly proportional; the slope serves as the constant of proportionality.
The proportionate change along the x and y axes never varies, hence the slope or increase is constant.
According to the question,
x(gallons) y(miles)
1 25
2 50
3 75
4 100
As we know, If y is proportional to x
=> y ∝ x
=> y = kx , where k is constant of proportionality
Using the table,
when x = 1 => y = 25
=> 25 = k(1)
=> k = 25
To know more about Constant of Proportionality here
https://brainly.com/question/29126727
#SPJ4
d. if a student was an undergraduate business major, what is the probability that the student intends to attend classes full-time in pursuit of an mba degree (to decimals)?
Answers
0.4
The probability that an undergraduate business major intends to attend classes full-time in pursuit of an MBA degree depends on the individual student's preferences and situation. Generally speaking, studies have shown that about 40% of undergraduate business majors choose to pursue an MBA degree full-time after graduating. Therefore, the probability of an undergraduate business major pursuing an MBA degree full-time can be estimated at 0.4.
Learn more about probability.
brainly.com/question/30034780
#SPJ11
T/F: the sdlc's planning phase yields a general overview of the company and its objectives.
Answers
True, the SDLC's planning phase yields a general overview of the company and its objectives. During this initial stage, the project's purpose, scope, and requirements are defined.
True. The planning phase of the Software Development Life Cycle (SDLC) is crucial in determining the direction and scope of the project. During this phase, the project team analyzes the company's goals, objectives, and requirements. This includes identifying the company's strengths, weaknesses, opportunities, and threats (SWOT analysis). The team also determines the feasibility of the project, identifies potential risks, and creates a plan for project execution. The planning phase yields a general overview of the company and its objectives, providing a solid foundation for the rest of the SDLC stages. It is essential to have a well-defined plan during this phase to ensure that the project aligns with the company's objectives and meets the expectations of the stakeholders.
Visit here to learn more about SDLC:
brainly.com/question/14096725
#SPJ11
there are between 25 and 43 students in a class
the ratio of boys to girls is 5 : 7
how many students are in the class?
Answers
Answer:
36
Step-by-step explanation:
Since the sum of the ratios is 5+7=12 the total number of students must be divisible by 12
The only number within the given range is 36
The number of students should be in the class should be considered as the 36.
Calculation of the number of students:Since
there are between 25 and 43 students in a class
the ratio of boys to girls is 5 : 7
So here the total ratio should be like
= 5 + 7
= 12
So here the number of students should be divisible by 12
So, it should be 36
Learn more about ratio here: https://brainly.com/question/13111469
what is the number of ways to order the 26 letters of the alphabet so that no two of the vowels a, e, i, o, and u occur consecutively?
Answers
There probability are 17,576,000 different ways to arrange the 26 letters of the alphabet so that the vowels a, e, I o, and u never appear back-to-back.
There are 21 consonants and 5 vowels (a,e,i,o,u) (all other letters).
The vowels can be arranged in 5! = 120 different ways.
The consonants can be arranged in 21! = 5,109,400,800 different ways.
The product of the two integers is 17,576,000, which is the total number of possible arrangements for all letters.
26 letters make up the alphabet, and 5 of them are vowels (a,e,i,o,u). We must determine how many ways there are to organize the vowels and consonants before we can determine how many ways there are to arrange the letters so that no two vowels appear consecutively.
There are 5! = 120 different ways to order the vowels. This is due to the fact that there are 5 vowels that must be grouped in various ways. Since there are 21 consonants that can be arranged, there are 21! = 5,109,400,800 different combinations that can be made. The product of the two integers is 17,576,000, which is the total number of possible arrangements for all letters.
Learn more about probability here
https://brainly.com/question/11234923
#SPJ4
7. Find the area of the rhombus. Express
your answer as a mixed number of
square centimeters in simplest form.
3 2/3cm
4½cm
Answers
Step 1
Convert
3 2/3
to an improper fraction.
Step 2
Convert
4 1/2
to an improper fraction.
Step 3
Cancel the common factor of 3.
Step 4
Combine
11 and 3/2
Step 5
Multiply
11
by
3.
The result can be shown in multiple forms.
Exact form: 33/2
Decimal form: 16.5
Mixed Number form: 16 1/2
Lines c and d are parallel lines cut by transversal p.
Horizontal and parallel lines c and d are cut by transversal p. On line c where it intersects with line p, 4 angles are formed. Clockwise, from uppercase left, the angles are: 1, 2, 3, 4. On line d where it intersects with line p, 4 angles are formed. Clockwise, from uppercase left, the angles are: 5, 6, 7, 8.
Answers
∠2 is congruent to ∠6 based on corresponding angle theorem.
What is corresponding angle theorem?Corresponding angles are formed when two parallel lines are intersected by a transversal line.The corresponding angles theorem states that "when a line intersects two parallel lines, the corresponding angles in the two regions of intersection are congruent."Assume that A, B, and C are distinct lines. Then A and B are parallel if and only if the corresponding angles of intersection of A and C, as well as B and Care, are equal.So here ,
Since in this question they are corresponding angles of parallel lines cut by a transversal, they are ∠2 ≅ ∠6 according to the Vertical Angles Theorem.
The complete question is : "Lines c and d are parallel lines cut by transversal p. Horizontal and parallel lines c and d are cut by transversal p. On line c where it intersects with line p, 4 angles are formed. Clockwise, from uppercase left, the angles are: 1, 2, 3, 4. On line d where it intersects with line p, 4 angles are formed. Clockwise, from uppercase left, the angles are: 5, 6, 7, 8. Which must be true by the corresponding angles theorem?"
To learn more about corresponding angle refer to :
https://brainly.com/question/3168048
#SPJ1
Dana just finished paying off the $15,400 loan she took out four years ago. The loan had 6. 68% interest, compounded monthly. If Dana paid a total of $18,321. 60, how much did she pay in service charges? a. $730. 08 b. $366. 49 c. $1,028. 72 d. $266. 76.
Answers
The perimeter of a square is 4s, where s is the length of one side.
Find the perimeter of the square at the right. Show unit analysis.
7 ft

Answers
Answer:
28ft.
Step-by-step explanation:
If \(s\) equals 7 and the perimeter equals 4 times \(s\), then the perimeter would be 4 times 7.
What is the decimal form of 45/120
Answers
Answer: 37.5 or 0.375
Step-by-step explanation:
to write 45/120 as a decimal you have to divide the numerator by the denominator of the fraction. we divide now 45 by 120 what we write down as 45/120 and get 0.375
Hope this helped!
Two years ago Juanita bought 2 shirts for $15 and last year she bought 4 shirts for $45. Assuming the prices will increase linearly, how much will 8 shirts cost Juanita this year?
Answers
Answer:
This year, Juanita will have to use $75.
Step-by-step explanation:
Because if 2 shirts is $15, 4 shirts will be $30. $45 is $15 more than $30, so the increase is $15. 2*4 is 8, so that will make it 15*4=60. 60+15=75.
Prove 2 n > n 2 by induction using a basis > 4: Basis: n 5 2A 25 Assume: Prove: Enter the rest of your proof in the box below.
Answers
We have proven that if the inequality holds true for k, it also holds true for k + 1. By the principle of mathematical induction, the inequality 2^n > n^2 holds true for all n > 4.
To prove the inequality 2^n > n^2 using induction with a basis greater than 4, we will use n=5 as the basis.
Basis: n = 5
2^5 = 32 and 5^2 = 25. Since 32 > 25, the inequality holds true for n = 5.
Now, we need to assume that the inequality holds true for an arbitrary positive integer k > 4, and then prove that it holds true for k + 1.
Assume: 2^k > k^2 for k > 4.
Prove: 2^(k + 1) > (k + 1)^2
Step 1: Multiply both sides of the assumption by 2.
2 * (2^k) > 2 * (k^2)
Step 2: Simplify the left side of the inequality.
2^(k + 1) > 2k^2
Step 3: Show that 2k^2 is greater than (k + 1)^2 for k > 4.
2k^2 > (k + 1)^2
2k^2 > k^2 + 2k + 1
Step 4: Rearrange the inequality to show that it holds true for k > 4.
k^2 - 2k - 1 > 0
Since k > 4, it is clear that k^2 - 2k - 1 > 0, as the left side increases as k increases.
Therefore, we have proven that if the inequality holds true for k, it also holds true for k + 1. By the principle of mathematical induction, the inequality 2^n > n^2 holds true for all n > 4.
Visit here to learn more about inequality:
brainly.com/question/30231190
#SPJ11
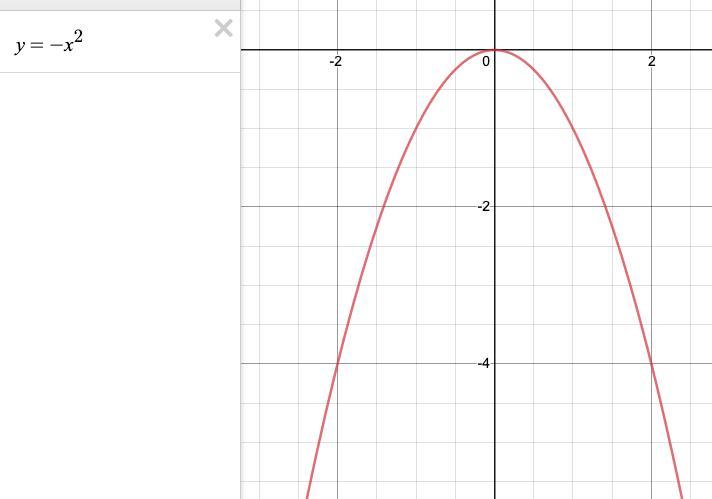
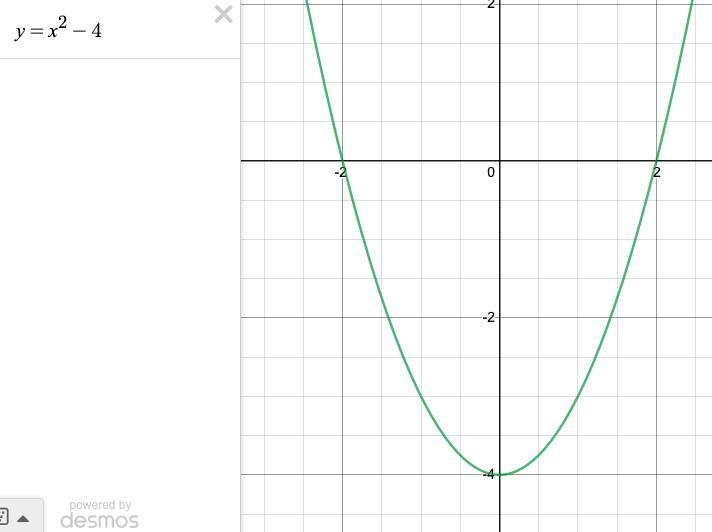
I KNOW IT'S A LOT BUT PLEASE HELP ME PLEASE I'VE TRIED FOR DAYS BUT DONT UNDERSTAND Step 1: For each given function below, make an XY table and plug in values for X (you make up the values). Step 2: Plug in values for each X into the equation to find Y values. Step 3: Plot the points in the table. TWO GRAPHS ONE y = -x2 OTHER y = x2 − 4 Then, once you have graphed both lines, use the coordinates of the vertex of each parabola and the Text Editor to explain whether the vertex is a maximum or minimum point of the graph, give the maximum or minimum value of the function, and describe the line of symmetry.

Answers
Answer: Take it one step at a time. The chart should have x values close to 0, both positive and negative. You get the y-values by substituting for x and working out the calculation.
Step-by-step explanation:
chart for y = -x² Remember you are squaring the (x) then multiply × -1 so all y-values are negative numbers.
x | y
-2 -4
-1 -1
0 0
1 -1
2 - 4
Plot those points on the graph, draw the parabola. It should look like the first graph attached. Since the vertex of the parabola is at the top, it is a maximum.
The parabola is a mirror image on either side of the y-axis, so that is the line of symmetry
Chart for y = x² –4 . figure x² first, then subtract 4
x . | . y
-2 0 . +4-2=0
-1 -3 +1 - 4 = -3
0 -4
1 -3
2 0
3 1 9 - 4 = 5
Your graph should look like the second (green) attached graph
I hope this is enough help for now.
type the Integra that makes the type the integral that makes the following multiplication sentence true * 7 equal -4
Answers
In order to determine the integer that makes true the given expression:
______ x 7 = -14
consider that such integer must be equal to the quotient between -14 and 7:
-14/7 = -2
In fact, you have:
-2 x 7 = -14
Hence, the integer is -2
![Solve (12) For F(x) =(12) = [?]3x+67](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/uBn5qeULxJNQl8gX45DoAzOhTiTQizoc.png)