Slope review
PROBLEM : What is the slope of the line whose equation has the following solutions? Give an exact number.
Solution: x = -2.5 y= 0.5
Solution: x=2 y = 2
The slope is:

Answers
To find slope, we must use the slope formula*.
\(m = \frac{2 - 0.5}{2 - (-2.5)} = \frac{1.5}{4.5}\)
The slope is 1.5/4.5.
Related Questions
The accompanying data fie contatis two predicior variablest-xt and ag, and a numenical targel variable, y. A regression tee will be constructed tring the data. Clich hero forthe forkloata fill a. Ust
Answers
We can construct a regression tree using the given data, we can use the rpart() function in R.
the specific instructions provided by the software or tool is used, as the steps may vary slightly depending on the platform. To construct a regression tree using the given data, follow these steps:
1. Open the data file that contains the predictor variables "XT" and "AG" and the numerical target variable "Y".
2. Check if the data is properly formatted and contains the necessary information for the regression tree.
3. If the data is in the correct format, proceed to build the regression tree.
4. Click on the provided link to access the software or tool that will help you create the regression tree.
5. Once you have access to the software, import the data file into the tool.
6. Specify the predictor variables ("XT" and "AG") and the target variable ("Y") for the regression tree.
7. Configure any additional settings or parameters as needed for your analysis.
8. Run the regression tree algorithm on the data.
9. Review the resulting regression tree, which will display the relationships between the predictor variables and the target variable.
10. Analyze the tree structure and interpret the findings to understand the impact of the predictor variables on the target variable.
Learn more about function from the following link,
https://brainly.com/question/11624077
#SPJ11
Random sample size of 81 are taken from an infinite population whose mean and standard deviation are 200 and 18, respectively. The distribution of the population is unknown. the mean and the standard error of the mean are?
Answers
Answer:
the mean and standard error of the mean are 200 and 2 respectively.
Step-by-step explanation:
Given that ;
the sample size n = 81
population mean μ = 200
standard deviation of the infinite population σ = 18
A population is the whole set of values, or individuals you are interested in, from an experimental study.
The value of population characteristics such as the Population mean (μ), standard deviation (σ) are said to be known as the population distribution.
From the given information above;
The sample size is large and hence based on the central limit theorem the mean of all the means is same as the population mean 200.
i.e
\(\mu = \bar \mu_x\) = 200
∴ The mean = 200
and the standard error of the mean can be determined via the relation:
\(\mathbf{standard \ error \ of \ mean = \dfrac{\sigma}{\sqrt {n}}}\)
\(\mathbf{standard \ error \ of \ mean = \dfrac{18}{\sqrt {81}}}\)
\(\mathbf{standard \ error \ of \ mean = \dfrac{18}{9}}\)
\(\mathbf{standard \ error \ of \ mean =2}\)
Therefore ; the mean and standard error of the mean are 200 and 2 respectively.
1. A car bought for $20,000. Its value depreciates by 10% each year for 3 years. What is the car's worth after3 years?
2. Find the perimeter of a circle whose radius is 3.5cm. (Take pi = 22/7)
3. The volume of a cone is 1540cm³. If its radius is 7cm, calculate the height of the cone. (Take pi = 22/7)
4. What is the coefficient of b in the expression b² - 5b +18
5. Expand (x +2) (9 - x)
7. Find x and y in the simultaneous equations. x + y = 4 3x + y = 8
8. Factorize a² +3ab - 5ab - 15b²
9. The bearing of a staff room from the assembly ground is 195degrees, what is the bearing of the assembly ground from the staff room?
Answers
Step-by-step explanation:
68$53++83(-$(7(3($++$
Explanation:
(x+2)(9-x)
= 9x - x^2 + 18 - 2x
= -x^2 + 7x + 18
B. compare his z-score in each event. c. compare his speed in each event. d. compare his pace in each event. questions 9-10 refer to the following situation: during a model railroad operating session, a model railroader must use the engine she is operating to move a pair of model cars through a series of track switches. her pair of cars consists of a boxcar and a flatcar. she knows that as the cars pass through the switches the boxcar has a 90% chance of getting through without derailing and the flatcar has an 80% chance of getting through without derailing. she also knows that whether either car derails or not is independent of the other car. 9. what is the probability that the flatcar derails? a. 10% b. 20% c. 28% d. 72% 10. what is the probability that both the boxcar and the flatcar get through without derailing? d. 72% c. 28% a. 10% b. 20%
Answers
To find the probability that the flatcar derails, we need to subtract the probability of it not derailing from 1. Since the flatcar has an 80% chance of getting through without derailing.
Therefore, the answer is b. 20%.
What is the probability that both the boxcar and the flatcar get through without derailing
Since the events of the boxcar and the flatcar derailing are independent, we can multiply their probabilities together.
The boxcar has a 90% chance of getting through without derailing (0.9) and the flatcar has an 80% chance (0.8), so the probability that both get through without derailing is
0.9 * 0.8 = 0.72 or 72%.
Therefore, the answer is d. 72%.
To know more about probability visit:
https://brainly.com/question/31828911
#SPJ11
Be a kind soul and help me out please

Answers
well, for the piece-wise function, we know that hmmm x = -1, -1 is less 1, so the subfunction that'd apply to that will be -2x + 1, because on that section "x is less than or equals to 1".
so f(-1) => -2(-1) + 1 => 3.
Answer:3
Step-by-step explanation:
In this case x=-1 so you will use the top equation because x<1
so f(-1) = -2(-1) + 1
= 2+1
=3
Which of the following describes the graph of y-√√-4x-36 compared to the parent square root function?
stretched by a factor of 2, reflected over the x-axis, and translated 9 units right
stretched by a factor of 2, reflected over the x-axis, and translated 9 units left
stretched by a factor of 2, reflected over the y-axis, and translated 9 units right
stretched by a factor of 2, reflected over the y-axis, and translated 9 units left
Save and Exit
Next
Submit
Answers
The statement that describes the graph of y-√√-4x-36 compared to the parent square root function is: d. stretched by a factor of 2, reflected over the y-axis, and translated 9 units left
What is graph?Stretch by a factor of 2: Multiply the input of the function by 2. The new function is f(2x).
Reflect over the y-axis: Negate the output of the function. The new function is -f(2x).
Translate 9 units left: Subtract 9 from the input of the function. The new function is -f(2x - 9). So if you have an original function f(x) the transformed function would be -f(2x - 9).
Therefore the correct option is d.
Learn more about graph here:https://brainly.com/question/19040584
#SPJ1
If is the probability that the reciprocal of a randomly selected positive odd integer less than 2010 gives a terminating decimal, with and being relatively prime positive integers, what is
Answers
The probability value of (m, n) is (1, 2^1005).
Let n be a positive odd integer. We are asked to find the probability that its reciprocal gives a terminating decimal. This is equivalent to saying that the only prime factors of n are 2 and 5 because any other prime factor will yield a repeating decimal.
If n is less than 2010, then its only possible prime factors are 3, 7, 11, ..., 2009, since all primes greater than 2009 are greater than n. We want n to have no prime factors other than 2 and 5. There are 1005 odd integers less than 2010.
We want to count how many of these have no odd prime factors other than 3, 7, 11, ..., 2009. This is equivalent to counting how many subsets there are of {3, 7, 11, ..., 2009}. There are 1004 primes greater than 2 and less than 2010. Each of these primes is either in a subset or not in a subset. Thus, there are 2^1004 subsets of {3, 7, 11, ..., 2009}, including the empty set.
Thus, the probability is:
P = (number of subsets with no odd primes other than 3, 7, 11, ..., 2009) / 2^1004
We can count this number using the inclusion-exclusion principle. Let S be the set of odd integers less than 2010. Let Pi be the set of odd integers in S that are divisible by the prime pi, where pi is a prime greater than 2 and less than 2010. Let Pi,j be the set of odd integers in S that are divisible by both pi and pj, where i < j.
Then, the number of odd integers in S that have no prime factors other than 2 and 5 is:
|S - ⋃ Pi + ⋃ Pi,j - ⋃ Pi,j,k + ...|
where the union is taken over all sets of primes with at least one element and less than or equal to 1005 elements.
By the inclusion-exclusion principle:
|S - ⋃ Pi + ⋃ Pi,j - ⋃ Pi,j,k + ...| = ∑ (-1)^k ⋅ (∑ |Pi1,i2,...,ik|)
where the outer summation is from k = 0 to 1005, and the inner summation is taken over all combinations of primes with k elements.
This simplifies to:
(1/2) ⋅ (2^1004 + (-1)^1005)
Thus, the probability is: P = (1/2^1004) ⋅ (1/2) ⋅ (2^1004 + (-1)^1005) = 1/2 + 1/2^1005. Hence, (m, n) = (1, 2^1005).
Learn more about probability:
https://brainly.com/question/31828911
#SPJ11
Complete question:
If m/n is the probability that the reciprocal of a randomly selected positive odd integer less than 2010 gives a terminating decimal, with m and n being relatively prime positive integers. what is probability value of m and n?
The probability value of (m, n) is (1, 2^1005).This is equivalent to saying that the only prime factors of n are 2 and 5 because any other prime factor will yield a repeating decimal.
Let n be a positive odd integer. We are asked to find the probability that its reciprocal gives a terminating decimal. This is equivalent to saying that the only prime factors of n are 2 and 5 because any other prime factor will yield a repeating decimal.
If n is less than 2010, then its only possible prime factors are 3, 7, 11, ..., 2009, since all primes greater than 2009 are greater than n. We want n to have no prime factors other than 2 and 5. There are 1005 odd integers less than 2010.
We want to count how many of these have no odd prime factors other than 3, 7, 11, ..., 2009. This is equivalent to counting how many subsets there are of {3, 7, 11, ..., 2009}. There are 1004 primes greater than 2 and less than 2010. Each of these primes is either in a subset or not in a subset. Thus, there are 2^1004 subsets of {3, 7, 11, ..., 2009}, including the empty set.
Thus, the probability is:
P = (number of subsets with no odd primes other than 3, 7, 11, ..., 2009) / 2^1004
We can count this number using the inclusion-exclusion principle. Let S be the set of odd integers less than 2010. Let Pi be the set of odd integers in S that are divisible by the prime pi, where pi is a prime greater than 2 and less than 2010. Let Pi,j be the set of odd integers in S that are divisible by both pi and pj, where i < j.
Then, the number of odd integers in S that have no prime factors other than 2 and 5 is:
|S - ⋃ Pi + ⋃ Pi,j - ⋃ Pi,j,k + ...|
where the union is taken over all sets of primes with at least one element and less than or equal to 1005 elements.
By the inclusion-exclusion principle:
|S - ⋃ Pi + ⋃ Pi,j - ⋃ Pi,j,k + ...| = ∑ (-1)^k ⋅ (∑ |Pi1,i2,...,ik|)
where the outer summation is from k = 0 to 1005, and the inner summation is taken over all combinations of primes with k elements.
This simplifies to:
\((1/2) * (2^{1004} + (-1)^1005)\)
Thus, the probability is: P = \((1/2)^{1004}* (1/2) *(2^{1004} + (-1)^{1005}) = 1/2 + 1/2^{1005}.\)
Hence, (m, n) = (\(1, 2^{1005\)).
Learn more about probability:
brainly.com/question/31828911
#SPJ11
Help me I don’t get this.

Answers
Answer:
i think its 105
Step-by-step explanation:
The power for a one-sided test of the null hypothesis = 10 versus the alternative = 8 is equal to 0.8. Assume the sample size is 25 and = 4. What is , the probability of a Type I error?
Answers
The probability of a Type I error is 0.2 or 20%. This means that there is a 20% chance of rejecting the null hypothesis when it is actually true.
The power of a hypothesis test is the probability of rejecting the null hypothesis when the alternative hypothesis is true. In this case, the power of the test is given as 0.8, and the null hypothesis is that the true value of the parameter is 10, while the alternative hypothesis is that the true value is 8.
We are given the sample size, n = 25, and the standard deviation, σ = 4. To calculate the probability of a Type I error, we need to determine the significance level of the test, denoted by α.
The significance level is the probability of rejecting the null hypothesis when it is actually true. It is usually set before conducting the test, and commonly set at 0.05 or 0.01.
To calculate α, we can use the following formula:
α = 1 - power = 1 - 0.8 = 0.2
So, the probability of a Type I error is 0.2 or 20%. This means that there is a 20% chance of rejecting the null hypothesis when it is actually true.
for such more question on probability
https://brainly.com/question/13604758
#SPJ11
Kala is driving on the highway. She begins the trip with 16 gallons of gas in her car. The car uses up one gallon of gas every 20 miles.
Let G represent the number of gallons of gas she has left in her tank, and let D represent the total distance (in miles) she has traveled. Write an equation relating G to D, and then graph your equation using the axes below.
Answers
Answer: G = 15-D/20
Step-by-step explanation:
Using the variables given,
G = 15 - D/20
please help me lol.

Answers
(3x2 + 7x + 10) - (3x2 - 12x - 10)
Answers
Answer:
19x + 20
I have a picture of my work here for an explanation

at bob's auto plaza there are currently new cars, used cars, new trucks, and used trucks. bob is going to choose one of these vehicles at random to be the deal of the month. what is the probability that the vehicle that bob chooses is used or is a truck? do not round intermediate computations, and round your answer to the nearest hundredth.
Answers
The probability that the vehicle Bob chooses is used or is a car is 0.6
There are 10 new cars, 4 used cars, 12 new trucks, and some used trucks at Bob's Auto Plaza. We are asked to find the probability that the chosen vehicle is used or is a car.
First, we need to find the total number of vehicles at the dealership:
Total number of vehicles = 10 new cars + 4 used cars + 12 new trucks + used trucks
We don't know how many used trucks there are, but we know that there are at least 4 of them (since there are 4 used cars). So the total number of vehicles is at least:
Total number of vehicles = 10 + 4 + 12 + 4 = 30
Now we need to find the number of vehicles that are used or cars. There are 4 used cars, and 10 new cars, for a total of 14 cars. There are also some used trucks, which we don't know the exact number of, but we know that there are at least 4 of them. So the total number of used or car vehicles is at least:
Total number of used or car vehicles = 4 used cars + 10 new cars + 4 used trucks = 18
To find the probability of choosing a used or car vehicle, we divide the number of used or car vehicles by the total number of vehicles:
Probability of choosing a used or car vehicle = Total number of used or car vehicles / Total number of vehicles
Probability of choosing a used or car vehicle = 18 / 30
Divide the numbers
Probability of choosing a used or car vehicle = 0.6
Learn more about probability here
brainly.com/question/11234923
#SPJ4
The given question is incomplete, the complete question is:
At Bob's Auto Plaza there are currently 10 new cars, 4 used cars, 12 new trucks, and used trucks, Bob is going to choose one of these vehices at random te be the Deal of the Month. What is the probability that the vehicle that Bob chooses is used or is a car? Do not round intermediate computations, and round your answer to the nearest hundredth
An architect wants to reduce a set of blueprints to make a portable set for easy access. The original dimensions of the blueprints are 24 inches by 36 inches. She reduces the blueprints by a scale factor of 13. She then decides that the reduced blueprints are a little too small and enlarges them by a scale factor of 1.25. Will the final image fit in a similar portfolio with an area of 160 square inches? Justify your response.
Answers
The final image will fit in a similar portfolio with an area of 160 square inches.
How to obtain the area of a rectangle?To obtain the area of a rectangle, you need to multiply its length by its width. The formula for the area of a rectangle is:
Area = Length x Width.
The dimensions for this problem are given as follows:
24 inches, 36 inches.
With the reduction with a scale factor of 1/3, the dimensions are given as follows:
8 inches, 12 inches.
With the enlargement by a factor of 1.25, the dimensions are given as follows:
10 inches and 15 inches.
Hence the area is given as follows:
15 x 10 = 150 square inches.
As the area of 150 square inches is less than 160 square inches, the final image will fit in a similar portfolio with an area of 160 square inches.
More can be learned about the area of a rectangle at brainly.com/question/25292087
#SPJ1
There are 50 kids taking archery at Bentwood Summer Camp. If 25% of the kids are taking archery, how many kids are at Bentwood Summer Camp in all?
Answers
Using the properties of percentages we can calculate that there are 200 kids in the archery camp that summer.
Long before the decimal numeral system, Ancient Rome routinely computed in fractions as multiples of 1/100.
A percentage is a dimensionless (pure) number; it has no unit of measurement.
The % value is determined by multiplying the numerical value of the ratio by 100. To calculate 50 apples as a percentage of 1250 apples, first compute 50/1250 = 0.04, then multiply by 100 to get 4%.
Let the total number of kids in the camp be x.
The number of kids who took archery = 25%
But 50 students took archery.
hence 25% of x = 50
Solving we infer:
x = 200
Therefore there are 200 kids in the camp.
To learn more about percentages visit:
https://brainly.com/question/15840409
#SPJ1
Marking brainliest
Please help

Answers
Answer:
Information
Step-by-step explanation:
The almanac was full of Information because it offered info to people about many things.
Hope this helped!!!! :D
(9,−7) after a dilation by a scale factor of 4 centered at the origin?
Answers
The image of the coordinates after a dilation of (9, −7) by a scale factor of 4 centered at the origin include the following: (36, -28).
What is dilation?In Geometry, dilation can be defined as a type of transformation which typically changes the size of a geometric object, but not its shape. This ultimately implies that, the size of the geometric object would be increased or decreased based on the scale factor used.
Next, we would have to dilate the coordinates of the preimage (9, -7) by using a scale factor of 4 centered at the origin as follows:
Coordinate A (9, -7) → Coordinate A' (9 × 4, -7 × 4) = Coordinate A' (36, -28).
In conclusion, the coordinates of the image after a dilation are (36, -28).
Read more on dilation here: brainly.com/question/20482938
#SPJ1
Help please I don’t think I have any idea with what I’m doing

Answers
If the triangles are similar but no congruent, then the triangles have different size, thus the only correct option is the dilation (first option).
Which transformation is the correct one?We know that two figures are congruent if the figures have the same shape and size, while two figures are similar only if have the same shape (but the figures can have different size).
Here we know that the triangles are similar but no congruent, so the triangles must have different size. From the given transformations, the only one that changes the size is the first option, a dilation.
And for example, if we apply a dilation AND the other transformations, then we still will get a similar figure, but if we apply a reflection/rotation/translation alones, we will get a congruent triangle.
Learn more about similar figures at:
https://brainly.com/question/14285697
#SPJ1
Unit:transformations homework 5 identifying transformations
Answers
The transformation given as A(-8,7) → A'(-8,-7) represents a reflection over x-axis .
In the reflection of the point (x,y) over x-axis transformation ,the x-coordinate of each point remains the same, but the y-coordinate is negated (changes sign).
Let's consider the coordinates of point A that is (-8, 7).
The transformation takes this point to A' (-8, -7).
We can see that the x-coordinate of the point remains the same which is -8. but , the y-coordinate changes from 7 to -7.
We know that in a reflection over the x-axis, the x-coordinate remains the same while the y-coordinate changes sign.
Therefore , the transformation that takes A to A' is a reflection over the x-axis.
Learn more about Transformations here
https://brainly.com/question/29208647
#SPJ4
The given question is incomplete , the complete question is
Identify the Transformation given as A(-8,7) → A'(-8,-7)?
Let Z ~ N(0, 1) and X ~ N(μ σ2) This means that Z is a standard normal random variable with mean 0 and variance 1 while X is a normal random variable with mean μ and variance σ2. Calculate E(Z3) (this is the third moment of Z)
Answers
Let's calculate E(Z^3), which is the third moment of Z, given that Z follows a standard normal distribution N(0, 1) and X follows a normal distribution N(μ, σ^2).
First, recall that the third moment of a random variable, E(Z^3), represents the expected value of the cube of Z. In this case, Z is a standard normal random variable, which has a symmetric probability density function (PDF) about the mean 0.
To calculate E(Z^3), we can use the formula:
E(Z^3) = ∫ z^3 * f(z) dz
where f(z) is the PDF of the standard normal distribution, and the integral is taken from negative infinity to positive infinity.
Since the PDF of Z is symmetric about the mean 0, the values of z^3 * f(z) will be positive for positive z values and negative for negative z values. These positive and negative values will cancel each other out when integrating over the entire range of Z, resulting in E(Z^3) = 0.
In summary, the third moment of Z, E(Z^3), for a standard normal random variable Z is 0 due to the symmetry of the PDF about the mean 0.
To know more about standard normal distribution refer here
https://brainly.com/question/29509087#
#SPJ11
√50-√18+√8+√128-3√2
Please solve this
Answers
Step-by-step explanation:
the
answer
of
this
question
is
9 \sqrt{2}
Do you like this (^__^) ??

The sequence of the differences, 2, 4, 8, 16, 32, … is a geometric sequence with:
Answers
Answer:
The first term as 2.
Pattern: Multiply the previous term and 2 to get the next term.
Step-by-step explanation:
The pattern is every term is 2× the previous term.
The sequence of the differences, 2, 4, 8, 16, 32, … is geometric. The pattern is every term is 2 times the previous term.
What is geometric series?The geometric series is a series in which the ratio of two consecutive numbers is constant.
The sequence of the differences, 2, 4, 8, 16, 32, … is geometric.
So, The ratio of two consecutive numbers is constant.
r = 4/2 = 2
r = 8/4 = 2
Thus, The pattern is every term is 2 times the previous term.
Learn more about geometric series;
https://brainly.com/question/13041183
#SPJ2
A study was conducted to estimate hospital costs for accident victims who wore seat belts. Twenty-one randomly selected cases have a distribution that appears to be approximately bell shaped with a mean of $9916 and a standard deviation of $5622. Complete parts (a) and (b). a. Construct the 95% confidence interval for the mean of all such costs. $
Answers
The 95% confidence interval for the mean of all such costs is $6986.4 to $12845.6.
Given that, Sample Mean = $9916
Sample Standard Deviation = $5622
Sample size, n = 21At 95% confidence level, the alpha level is 0.05.
The degrees of freedom (df) are n - 1 = 20.
Standard Error (SE) is given by the formula:
SE = (Sample Standard Deviation/ √(Sample Size))
SE = 5622/ √21SE = 1223.8
The formula for confidence interval at 95% is as follows:
Confidence Interval = (Sample Mean - (Critical value*SE), Sample Mean + (Critical value*SE))
Now we need to find the critical value at 95% using t-distribution since the sample size is less than 30.
The degrees of freedom (df) are 20.
So, t-value at 95% confidence and df = 20 is ±2.093.
Substituting the given values in the above formula we get,
Confidence Interval = ($9916 - (2.093*1223.8), $9916 + (2.093*1223.8))
Confidence Interval = ($6986.4, $12845.6)
Hence, the 95% confidence interval for the mean of all such costs is $6986.4 to $12845.6.
Know more about 95% confidence interval here:
https://brainly.com/question/15712887
#SPJ11
Suppose their is a 1.6 f drop in temperature for every thousand feet that an airplane climbs into the sky. if the temperature on the ground is 55.2 f what will be the temperature when the plane reaches an altitude of 5000 ft
Answers
Answer:
Step-by-step explanation:
The temperature when the plane reaches an altitude of 5000 ft will be 47.2 F.
Temperature Drop per 1000 ft : 1.6 F
Temperature Drop for 5000 ft : 1.6 x (5000/1000)
: 1.6 x 5 = 8.0
Temperature at 5000 ft : 55.2 – 8 = 47.2 F
#1234
The temperature when the plane reaches an altitude of 5000 feet will be 47.2 Fahrenheit.
In the given case, there is a drop of 1.6 Fahrenheit in temperature for every thousand feet that an airplane climbs into the sky.
The temperature on the ground is 55.2 Fahrenheit.
Temperature Drop per 1000 feet = 1.6 Fahrenheit
Temperature Drop for 5000 feet = 1.6 x (5000/1000)
= 1.6 x 5
= 8.0 Fahrenheit
To get the temperature when the plane reaches an altitude of 5000 feet,
The temperature at 5000 feet = 55.2 – 8 = 47.2 Fahrenheit
To learn more about Fahrenheit click here:
brainly.com/question/516840
#SPJ4
I NEED HELP ASAPPPPP graph the image of the figure after a dilation with a scale factor of 1/2 centered at (-1,3)
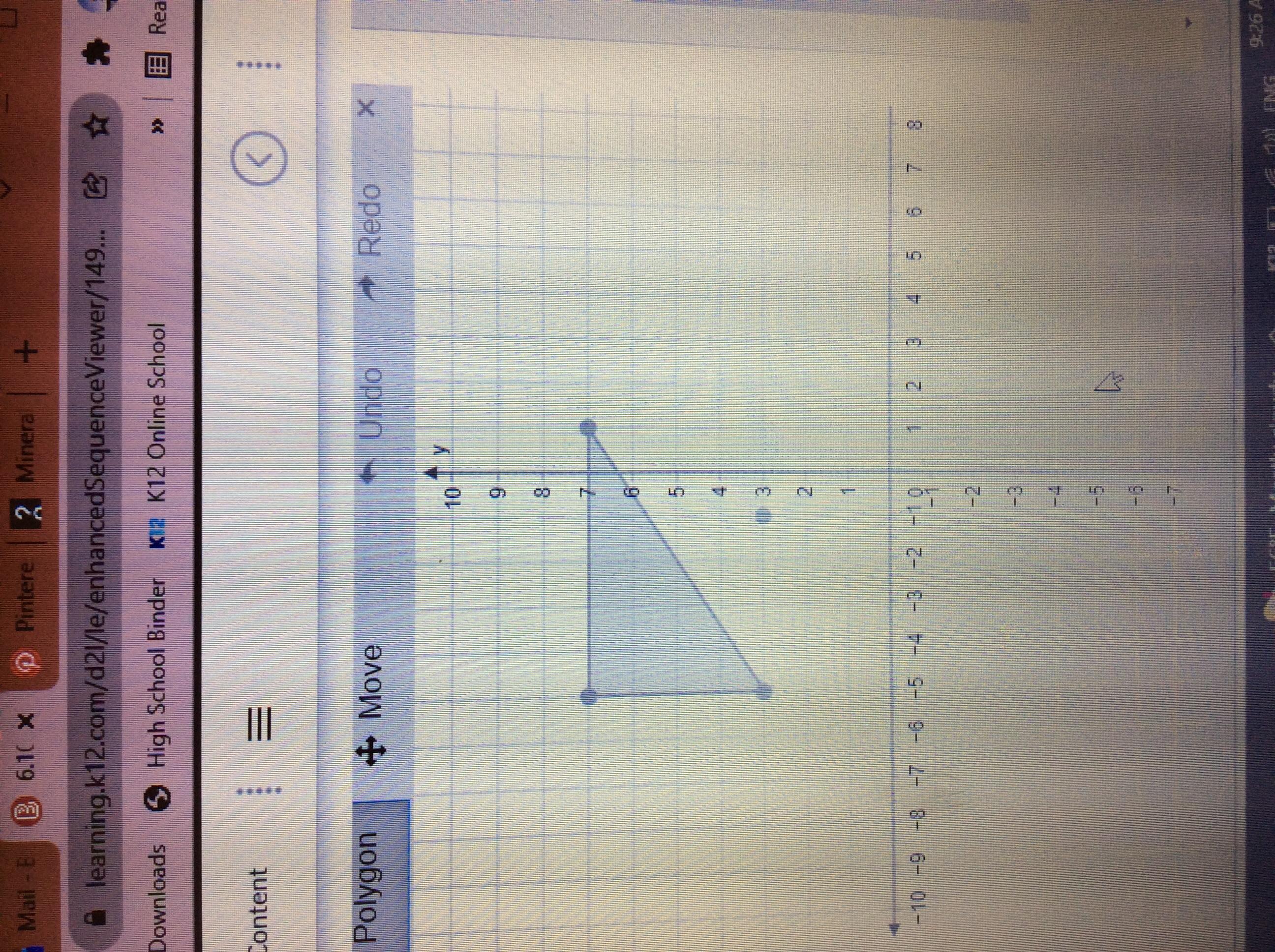
Answers
Answer:
so it would be 1/2 /1/3 = 1 1/2
Step-by-step explanation:
Dividing two fractions is the same as multiplying the first fraction by the reciprocal (inverse) of the second fraction.
Take the reciprocal of the second fraction by flipping the numerator and denominator and changing the operation to multiplication. Then the equation becomes
12×31=?
For fraction multiplication, multiply the numerators and then multiply the denominators to get
1×32×1=32
This fraction cannot be reduced.
The fraction
32
is the same as
3÷2
Convert to a mixed number using
long division for 3 ÷ 2 = 1R1, so
32=112
Therefore:
12÷13=112
What is the measure of an exterior angle of an equilateral triangle?
Answers
Answer:
120
Step-by-step explanation:
An equilateral triangle has 3 sides. The exterior angle = 360 / 3 = 120
A square has 4 sides. Each exterior angle = 360 / 4 = 90
A regular n gon has n sides. The exterior angles will be 360/n
a fraction has a denominator of 20. the numerator has the value of “x less than the denominator” if the fraction is equivalent to 1/4, what i’d the value of x?

Answers
Answer:
First what you want to do is find what fraction is equal to 1/4 and has a denominator of 20.
The way you can find this is by taking 1/4 and seeing how many times the denominator or 4 will go into 20.
4 * 5 = 20
Since 4 times 5 is 20, we will multiply 5 to the numerator of the fraction to.
1 * 5 = 5
So 5/20 is = to 1/4
x = 5
Now the question says, " x less thsn the denominator" so we just need to find how much less is 5 compared to 20.
20 - 5 = 15
The numerator has a value, "15 less than the denominator."
Step-by-step explanation:
Hope this helps! =D
A pizza lover wants to compare the average delivery times for four local pizza restaurants. Over the course of a few weeks, he orders a number of pizzas from each restaurant, and he records the time it takes for each pizza to be delivered.
a) When performing an ANOVA with this data, what is the alternative hypothesis?
- All of the restaurants have different mean delivery times
- At least two of the restaurants have different mean delivery times
- Two of the restaurants have different mean delivery times
- One of the restaurants has a different mean delivery time than the others
b) A partial ANOVA table for his data is shown below. What is the value of B?
Source DF SS MS F P-value
Treatment B 19.31 D F G
Error C 15.667 E
Total 18 34.977
What is the value of C in the ANOVA table?
d) What is the value of D in the ANOVA table? Give your answer to three decimal places.
e) What is the value of E in the ANOVA table? Give your answer to three decimal places.
f) What is the value of F in the ANOVA table? Give your answer to two decimal places.
g) What is the value of G in the ANOVA table? Give your answer to four decimal places.
h) Using a 0.1 level of significance, what should his conclusion be in this case?
- He should conclude that at least two of the restaurants have different mean delivery times because the P-value is less than 0.1.
- He should fail to reject the claim that at all of the restaurants have the same mean delivery times because the P-value is greater than 0.1.
- He should conclude that at least two of the restaurants have different mean delivery times because the P-value is greater than 0.1.
- He should conclude that at all of the restaurants have the same mean delivery times because the P- value is less than 0.1.
Answers
(a) When performing an ANOVA with the data the alternative hypothesis is at least two of the restaurants have different mean delivery times.
(b)75.8
Analysis of variance. or ANOVA, is a statistical method that separate observed variance data into different components to use for additional tests. A one way ANOVA is used for three or more groups of data, to gain information about the relationship between the dependent and independent variables.
The ANOVA table shows how the sum of squares are distributed according to source of variation, and hence the mean sum of squares.
It is given that a pizza lover wants to compare the average delivery times.
Therefore the null hypothesis and alternate hypothesis implies that,
H₀ = all restaurants have equal mean delivery time
Hₐ = at least two restaurants have different two deliveries
Hence the alternate hypothesis for performing an ANOVA with the data is at least two of the restaurants have different mean delivery times.
The alternate hypothesis (Hₐ) defines that there is a statistically important relationship between two variables. Whereas null hypothesis states that is no statistical relationship between the two variables.
To know more about hypothesis here
https://brainly.com/question/14517618
#SPJ4
What is the slope and y-intercept of the given equation?
y = 2/3x + 5
Answers
Answer:
The slope is 2/3x and the y-intercept is 5.
6. Simplify:
√900+ √0.09+√0.000009
Answers
The simplified value of the expression √900 + √0.09 + √0.000009 is 30.303.
To simplify the given expression, let's evaluate the square roots individually and then perform the addition.
√900 = 30, since the square root of 900 is 30.
√0.09 = 0.3, as the square root of 0.09 is 0.3.
√0.000009 = 0.003, since the square root of 0.000009 is 0.003.
Now, we can add these simplified values together
√900 + √0.09 + √0.000009 = 30 + 0.3 + 0.003 = 30.303
Therefore, the simplified value of the expression √900 + √0.09 + √0.000009 is 30.303.
for such more question on expression
https://brainly.com/question/4344214
#SPJ8