sin²A-cos²A=2sin²A-1
Answers
\(\sin^2\alpha-\cos^2\alpha=2\sin^2\alpha-1\\\sin^2\alpha+\cos^2\alpha=1\)
This is the Pythagorean identity, therefore \(\alpha\in\mathbb{R}\).
Step-by-step explanation:
please mark me as brainlest

Related Questions
x(6-x) in standard form
Answers
Do you think the line on the graph in problem 1 is a good one for this scatter plot? Explain your answer.
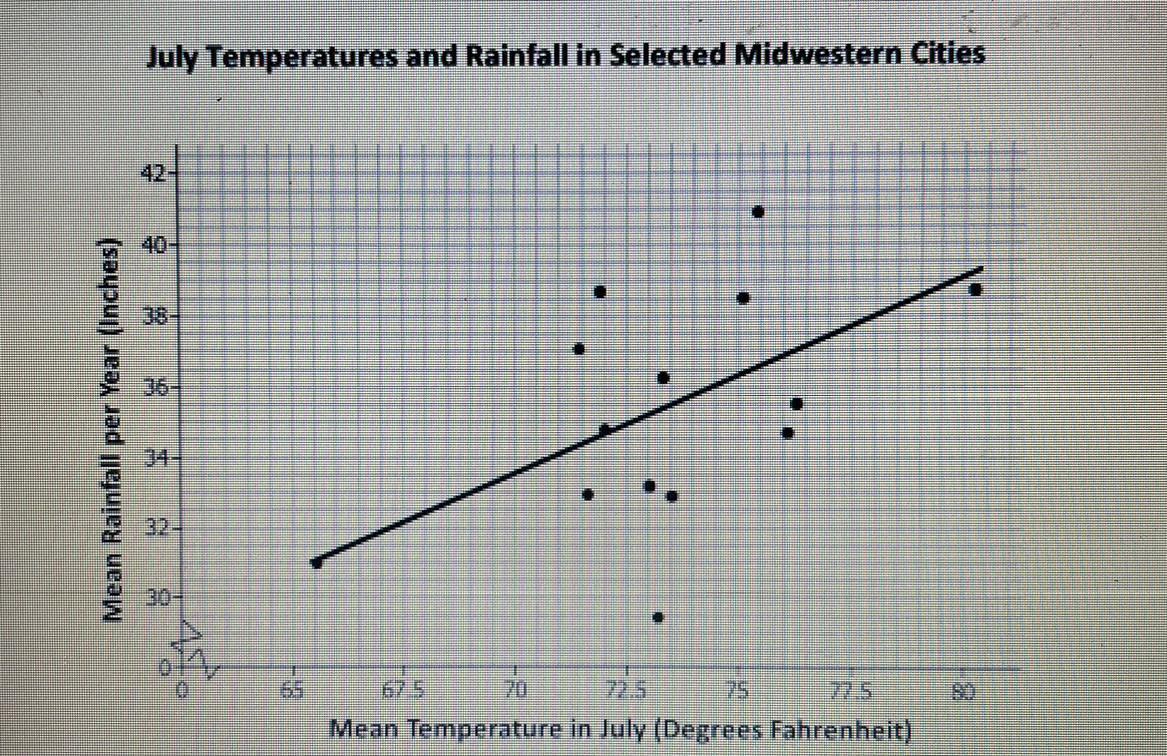
Answers
The line created is a good representation of a line of best fit
How to determine the true statementFrom the question, we have the following parameters that can be used in our computation:
The graph
On the graph, we can see that the line divides the points on the line evenly
A good line of best fit would have approximately equal number of points on either sides
Hence, the line is a good representation
Read more about line of best fit at
brainly.com/question/1441182
#SPJ1
Use the appropriate expression for the differential surface area ds to determine the area of each of the following surfaces:
a. 2 ≤ r ≤ 5, φ - π/4, -2 ≤ z ≤ 2
b. R = 2, 0 ≤ θ ≤ π/3, 0 ≤ φ ≤ π
Answers
a)The surface area of the given surface, we use the expression ds = r dφ dz dr and substitute the limits of integration. b)The surface area of the given surface, we use the expression ds = R^2 sin(θ) dθ dφ and substitute the limits of integration.
a. The surface described in part a can be defined in cylindrical coordinates as follows: 2 ≤ r ≤ 5 (radius), φ - π/4 (azimuthal angle), -2 ≤ z ≤ 2 (height). To determine the surface area, we can use the expression for the differential surface area in cylindrical coordinates, which is given by ds = r dφ dz dr.
1. We start by integrating with respect to r. The limits for r are 2 and 5. So, the integral becomes ∫[2,5] r dφ dz.
2. Next, we integrate with respect to φ. The limits for φ are -π/4 and π/4. The integral now becomes ∫[-π/4,π/4] ∫[2,5] r dz dφ.
3. Finally, we integrate with respect to z. The limits for z are -2 and 2. The integral becomes ∫[-π/4,π/4] ∫[2,5] ∫[-2,2] r dz dφ.
4. Evaluating the integral, we obtain the surface area of the given surface.
b. The surface described in part b can be defined in spherical coordinates as follows: R = 2 (radius), 0 ≤ θ ≤ π/3 (polar angle), 0 ≤ φ ≤ π (azimuthal angle). To determine the surface area, we can use the expression for the differential surface area in spherical coordinates, which is given by ds = R^2 sin(θ) dθ dφ.
1. We start by integrating with respect to φ. The limits for φ are 0 and π. So, the integral becomes ∫[0,π] R^2 sin(θ) dθ dφ.
2. Next, we integrate with respect to θ. The limits for θ are 0 and π/3. The integral now becomes ∫[0,π] ∫[0,π/3] R^2 sin(θ) dθ dφ.
3. Evaluating the integral, we obtain the surface area of the given surface.
Learn more about area : brainly.com/question/1631786
#SPJ11
Express the situation as an integer in the space provided. A gain of 56 points in a game
Answers
Evaluate the following: 3 to the power 2 ÷ (2 + 1). 2 3 4 5
Answers
Answer:
3
Step-by-step explanation:
The sales of a particular brand of children's athletic shoes rose from $4,500,000 to $5,400,000. Find the percent of increase in sales. Round to the nearest tenth of a percent, if necessary
1. 0.2%
2. 20%
3. 16.7%
4. 83.3%
Answers
explanation: divide the difference between the two amounts by the original amount.
900,000 / 4,500,500 = .2
next you multiply by 100 to make it into a percentage instead of a decimal.
.2 x 100 = 20
20%
Compute the Taylor polynomial T5(x) and use the Error Bound to find the maximum possible size of the error. f(x) cos(x), a = 0, x = 0.1
Answers
The Taylor polynomial T₅(x) is 0.99500416 and by use the Error Bound the maximum possible size of the error is 49943.1 × 10⁻⁷.
What is Taylor Series?
The Taylor series or Taylor expansion of a function in mathematics is the infinite sum of terms represented in terms of the function's derivatives at one particular point. The function and the sum of its Taylor series are roughly equivalent for the majority of typical functions at this point.
Taylor series or Taylor expansion:
Infinity ∑ (n = 0) fⁿ(a)/n! (x - a)ⁿ
Where,
n! = factorial of n
a = real or complex number
fⁿ(a) = nth derivative of function f evaluated at the point a.
As given function is,
f(x) = cosx, a = 0, x = 0.1
Taylor polynomial of degree 'n' for f(x) center a,
Tₙ(x) = f(a) + f'(a)(x - a) + f''(a)/2 (x - a)² + f'''(a)/3 (x - a)³ + ......+ fⁿ⁻¹(a)/(n - 1)! (x - a)ⁿ⁻¹ + fⁿ(a)/n! (x - a)ⁿ
Evaluate values as follows:
f(x) = cosx ⇒ f(0) = 1
f'(x) = -sinx ⇒ f'(0) = 0
f''(x) = -cosx ⇒ f''(0) = -1
f'''(x) = sinx ⇒ f'''(0) = 0
f⁴(x) = cosx ⇒ f⁴(0) = 1
f⁵(x) = -sinx ⇒ f⁵(0) = 0
Substitute obtained values in Taylor series,
T₅(x) = 1 + (0) (x - 0) + (-1)/2 (x - 0)² + 0 + 1/24(x - 0)⁴ + 0
T₅(x) = 1 -1/2x² + 1/24x⁴
At x = 0.1
T₅(0.1) = 1 -1/2(0.1)² + 1/24(0.1)⁴
T₅(0.1) = 1 - 0.005 + 4.16 × 10⁻⁶
T₅(0.1) = 0.99500416
Hence, the Taylor polynomial T₅(x) is 0.99500416.
Evaluate the maximum possible size of the error:
cos(0.1) = 0.99999847
T₅(0.1) = 0.99500416
Icos(0.1) - T₅(0.1)I = 0.99999847 - 0.99500416
Icos(0.1) - T₅(0.1)I = 0.00499431
Icos(0.1) - T₅(0.1)I = 49943.1 × 10⁻⁷.
Hence, the Error Bound the maximum possible size of the error is 49943.1 × 10⁻⁷.
To learn more about Taylor polynomial from the given link.
https://brainly.com/question/2533683
#SPJ4
PLEASE HELP WILL GIVE BRAINLIEST!!!

Answers
Answer: Choice B) Investment decreases by 3% each month
=====================================================
Explanation:
We won't use the value 2500 at all.
The base of the exponential is 0.97
Set this equal to 1+r and solve for r
1+r = 0.97
r = 0.97-1
r = -0.03
The negative r value indicates we have exponential decay, so the value of the investment decreases by 3% each month.
Let's say you had $100 to start off. This would mean the investment would be worth $97 after one month is up.
The circumference of the Earth is approximately 40,000 km. If you made a circle of wire around the globe, that is only 10 meters (0.01 km) longer than the circumference of the globe, select ALL the creatures that could creep under the wire.
Group of answer choices
a. a flea
b. a mouse
c. a person
d. none of the above
Answers
A manufacturer has a steady annual demand for 15,000 cases of sugar. It costs $10 to store 1 case for 1 year, $30 in set up cost to produce each batch, and $16 to produce each case. Find the number of cases per batch that should be produced to minimize cost.

Answers
The number of cases per batch that should be produced to minimize cost is: 300 units
How to find the economic order quantity?The number of cases per batch that should be produced to minimize cost can be found by using the Economic Order Quantity.
The Economic Order Quantity (EOQ) is a calculation performed by a business that represents the ideal order size that allows the business to meet demand without overspending. The inventory manager calculates her EOQ to minimize storage costs and excess inventory.
Thus:
Number of cases per batch = √((2 * Setup costs * annual demand)/ holding costs for the year)
Solving gives:
√((2 * 30 * 15000)/10)
= √90000
= 300 units
Read more about Economic Order Quantity at: https://brainly.com/question/26814787
#SPJ1
During a storm, an apartment building lost power for 26 hours. For how many
seconds was the power out?
A 3744 seconds
B. 156 seconds
C. 6400 seconds
D. 9360 seconds
Answers
Answer:
d.9360
Step-by-step explanation:
if it was c the hours wouldve probably been 23 hr or 24hr
Find the 49th term.
-15, -10, -5, O, 5, ...
49th term = [?]
1st term + common difference(desired term - 1)
Enter
Answers
Answer:
49th term = 225
Step-by-step explanation:
The following sequence: -15, -10, -5, 0, -5... is an example of an arithmetic progression.
An arithmetic progression or AP for short, is a sequence in which the difference between successive terms is constant. This difference is known as the common difference, and can be found by subtracting a term by its preceding term.
The general formula, for the nth term of an arithmetic progression, is thus:
Tn = a + (n - 1)d, where a = first term, and d = common difference.
In the sequence: -15, -10, -5, 0, 5...,
a = -15, and d = -10--15 = 5
T49 = -15 + (49 - 1)5 = 225
∴ 49th term = 225
a. find the solution of the given initial value problem. g b. plot a graph of the solution. y′′ 4y = ( t − ) − ( t − 2 ) ; y(0) = 0, y′(0) = 0
Answers
The particular solution satisfying the initial conditions is y(t) = (1/2)*cos(2t) - (1/8)*sin(2t) + (1/4)t - 1/2 and the graph has been plotted.
The given differential equation is y′′ + 4y = (t − ) − (t − 2). To solve this equation, we will first find the general solution to the homogeneous part, y′′ + 4y = 0, and then find a particular solution to the non-homogeneous part, (t − ) − (t − 2).
The characteristic equation for the homogeneous part is obtained by assuming the solution is of the form. Substituting this into the equation, we get r² + 4 = 0. Solving this quadratic equation, we find two complex roots: r = ±2i. Therefore, the general solution to the homogeneous part is y_h(t) = c₁cos(2t) + c₂sin(2t), where c₁ and c₂ are arbitrary constants.
To find a particular solution to the non-homogeneous part, we will use the method of undetermined coefficients. Since the non-homogeneous part contains terms (t − ) and (t − 2), we assume a particular solution of the form y_p(t) = At + B, where A and B are constants to be determined.
Taking the derivatives, we have y′_p(t) = A and y′′_p(t) = 0. Substituting these into the differential equation, we get 0 + 4(At + B) = (t − ) − (t − 2). Equating the coefficients of the like terms on both sides, we get 4A = 1 and 4B = -2.
Solving these equations, we find A = 1/4 and B = -1/2. Thus, the particular solution is y_p(t) = (1/4)t - 1/2.
The general solution to the original differential equation is given by the sum of the homogeneous and particular solutions: y(t) = y_h(t) + y_p(t).
y(t) = c₁cos(2t) + c₂sin(2t) + (1/4)t - 1/2.
We are given the initial conditions y(0) = 0 and y′(0) = 0.
Substituting these values into the general solution, we get:
y(0) = c₁cos(0) + c₂sin(0) + (1/4)*0 - 1/2 = 0.
This equation simplifies to c₁ - 1/2 = 0, which gives c₁ = 1/2.
Differentiating the general solution with respect to t, we get:
y′(t) = -2c₁sin(2t) + 2c₂cos(2t) + 1/4.
Substituting t = 0 and y′(0) = 0 into the above equation, we have:
y′(0) = -2c₁sin(0) + 2c₂cos(0) + 1/4 = 0.
This equation simplifies to 2c₂ + 1/4 = 0, which gives c₂ = -1/8.
Therefore, the particular solution satisfying the initial conditions is:
y(t) = (1/2)*cos(2t) - (1/8)*sin(2t) + (1/4)t - 1/2.
The graph will show how the solution varies with the input value t. It will illustrate the oscillatory nature of the cosine and sine functions, along with the linear term (1/4)t, which represents a gradual increase. The initial condition y(0) = 0 ensures that the graph passes through the origin, and y′(0) = 0 implies the absence of an initial velocity.
To know more about graph here
https://brainly.com/question/17267403
#SPJ4

21) One and two-tenths squared = ?
Answers
\(1+(0.2)^2=1+0.04=\boxed{1.04}\)
Answer:
1.44
Step-by-step explanation:
1 2/10 squared = 1.44
Suggest regular languages L1 and L2 over {0,1} such that 1. L1⊈L2, 2. L2L1, and 3. (L1∪L2)∗=L1∗∪L2∗ (b) Prove or disprove whether condition 3 above holds for any regular languages, L1 and L2.
Answers
a). We have proved all the given conditions.
b). It is true that condition 3 holds for all regular languages L1 and L2.
(a) Regular languages L1 and L2 can be suggested as follows:
Let \(L_1={0^{(n+1)} | n\geq 0}\)
and
\(L_2={1^{(n+1)} | n\geq 0}\)
We have to prove three conditions:1. L1 ⊈ L2:
The given languages L1 and L2 both are regular but L1 does not contain any string that starts with 1.
Therefore, L1 and L2 are distinct.2. L2 L1:
The given languages L1 and L2 both are regular but L2 does not contain any string that starts with 0.
Therefore, L2 and L1 are distinct.3. (L1 ∪ L2)* = L1* ∪ L2*:
For proving this condition, we need to prove two things:
First, we need to prove that (L1 ∪ L2)* ⊆ L1* ∪ L2*.
It is clear that every string in L1* or L2* belongs to (L1 ∪ L2)*.
Thus, we have L1* ⊆ (L1 ∪ L2)* and L2* ⊆ (L1 ∪ L2)*.
Therefore, L1* ∪ L2* ⊆ (L1 ∪ L2)*.
Second, we need to prove that L1* ∪ L2* ⊆ (L1 ∪ L2)*.
Every string that belongs to L1* or L2* also belongs to (L1 ∪ L2)*.
Thus, we have L1* ∪ L2* ⊆ (L1 ∪ L2)*.
Therefore, (L1 ∪ L2)* = L1* ∪ L2*.
Therefore, we have proved all the given conditions.
(b)It is true that condition 3 holds for all regular languages L1 and L2.
This can be proved by using the fact that the union of regular languages is also a regular language and the Kleene star of a regular language is also a regular language.
To know more about string, visit:
https://brainly.com/question/30099412
#SPJ11
56 x 1/8 tell me please
Answers
cancel out the common factor of 8
Answer:
7
Step-by-step explanation:
its 7 hope this helps!!!!
if U={1,2,3,4,5,6,7,8},A={1,2,3,4},B={3,4,5,6,7}.find(AUB)'
Answers
Answer:
12345678910
iya lina beb
The Math Club at Foothill College is planning a fundraiser for ë day. They plan to sell pieces of apple pie for a price of $4.00 each. They estimate that the cost to make x servings of apple pie is given by, C(x) = 300+ 0.1x +0.003x². Use this information to answer the questions below: (A) What is the revenue function, R(x)? (B) What is the associated profit function, P(x). Show work and simplify your function algebraically. (C) What is the marginal profit function? (D) What is the marginal profit if you sell 150 pieces of pie? Show work and include units with your answer. (E) Interpret your answer to part (D).
Answers
The marginal profit if you sell 150 pieces of pie is $1.20 per piece.E. The marginal profit if you sell 150 pieces of pie is the additional profit made by selling one more unit of a good.
Given,The cost to make x servings of apple pie is C(x) = 300+ 0.1x +0.003x².
The price to sell one piece of pie is $4.00.So, the revenue function, R(x) can be written asR(x) = price per unit × number of units soldR(x) = 4x.
The profit function, P(x) is given by the difference between the revenue function and cost function i.e.,P(x) = R(x) - C(x)
Substituting R(x) = 4x and C(x) = 300 + 0.1x + 0.003x² in P(x), we haveP(x) = 4x - (300 + 0.1x + 0.003x²)
P(x) = 4x - 300 - 0.1x - 0.003x²
P(x) = - 0.003x² + 3.9x - 300.
The marginal profit function is given by P'(x) = R'(x) - C'(x).Let's find R'(x) and C'(x).Differentiating R(x) = 4x with respect to x, we getR'(x) = 4Differentiating C(x) = 300 + 0.1x + 0.003x² with respect to x, we getC'(x) = 0.1 + 0.006x.
Substituting R'(x) = 4 and C'(x) = 0.1 + 0.006x in P'(x), we getP'(x) = 4 - (0.1 + 0.006x)P'(x) = 3.9 - 0.006x.
Now, let's find the marginal profit if we sell 150 pieces of pie.
Substituting x = 150 in P'(x), we getP'(150) = 3.9 - 0.006 × 150P'(150) = $1.20 per piece.
The marginal profit if we sell 150 pieces of pie is $1.20 per piece.
The marginal profit is the additional profit made by selling one more unit of a good.So, if we sell one more piece of pie, the profit will increase by $1.20.
To know more about profit function visit :-
https://brainly.com/question/16458378
#SPJ11
Frank bought 5 hot dogs and 9 bottles of apple juice for his brother's birthday party what is the ratio of hot dogs two bottles of apple juice
Answers
Answer:
5 : 9
Step-by-step explanation:
You combine the two values that you have been given (5 and 9) to get the ratio of hot togs to apple juice.
hope this helpsss :)
Normal probability distribution is applied to: A. a subjective random variable B. a discrete random variable C. any random variable D. a continuous random variable
Answers
Normal probability distribution is applied to a continuous random variable. The correct option is D.
The normal probability distribution, also known as the Gaussian distribution, is a probability distribution that is commonly used in statistics and probability theory. It is a continuous probability distribution that is often used to model the behavior of a wide range of variables, such as physical measurements like height, weight, and temperature.
The normal distribution is characterized by two parameters: the mean (μ) and the standard deviation (σ). It is a bell-shaped curve that is symmetrical around the mean, with the highest point of the curve being located at the mean. The standard deviation determines the width of the curve, and 68% of the data falls within one standard deviation of the mean, while 95% falls within two standard deviations.
The normal distribution is widely used in statistical inference and hypothesis testing, as many test statistics are approximately normally distributed under certain conditions. It is also used in modeling various phenomena, including financial markets, population growth, and natural phenomena like earthquakes and weather patterns.
Overall, the normal probability distribution is a powerful tool for modeling and analyzing a wide range of continuous random variables in a variety of fields.
To learn more about continuous random variable refer here:
https://brainly.com/question/17238189
#SPJ11
∠VTW≅∠UTW and ∠U≅∠V. Complete the proof that
VW
≅
UW
.
T
U
V
W
Answers
Answer: did you make that up ??
Step-by-step explanation:
Answer:
A. Alternate interior
B. Transitive property
C. Converse alternate interior angles theorem.
A factory produced a batch of 0.07 m³ of
apple juice.
2000 cm³ of apple juice was removed from
the batch for quality testing.
Calculate how much apple juice was left in
the batch.
3
Give your answer in cm³

Answers
The initial batch size is given as 0.07 m³, which is equivalent to 70,000 cm³ (since 1 m³ = 1,000,000 cm³).
The quantity removed for quality testing is given as 2000 cm³.
Therefore, to find the remaining apple juice, we'll subtract 2000 cm³ from 70,000 cm³:
70,000 cm³ - 2000 cm³ = 68,000 cm³
So, there are 68,000 cm³ of apple juice left in the batch.
if you triple a number and add 2, the result is 8 more than the number.
Answers
Answer:
3x+2=8
X=2
Step-by-step explanation:
3x+2=8
3x=6
X=2
Hopes this help please mark brainliest
Write as a verbal expression

Answers
The verbal expression for equation 10+y is "10 is added to variable y"
Verbal expression:Standardized terms for verbal expressions in mathematics help translate mathematical expressions into written form.
To solve the given word problems, we need to translate the given verbal expression into a mathematical expression using Mathematical operations like adding, subtracting, multiplication and division.
Here we have
Mathematical expression 10 + y
Here 10 is the numerical value and y is a variable combined with the symbol Plus (+) which indicates 10 and y are added together
Therefore,
The verbal expression for equation 10+y is "10 is added to variable y"
Learn more about Verbal expression at
https://brainly.com/question/10047973
#SPJ1
What is the circumference of the circle? Use 3.14 pi
Answers
Answer: multiply the diameter of the circle with π (pi). The circumference can also be calculated by multiplying 2×radius with pi (π=3.14)
Step-by-step explanation:
becaue... multiply the diameter of the circle with π (pi). The circumference can also be calculated by multiplying 2×radius with pi (π=3.14)
helppp i’ll give brainliest

Answers
Answer:
6 x 10^-4 (B)
Step-by-step explanation:
It is the greater number.
if a fair die is rolled 5 times, what is the probability, rounded to the nearest thousandth, of getting at least 2 fours?
Answers
So the probability, rounded to the nearest thousandth, of getting at least 2 fours in 5 rolls of a fair die is 0.194.
What is the simple definition of probability?A probability is a number that expresses the possibility or likelihood that a specific event will take place. Probabilities can be stated as proportions with a range of 0 to 1, or as percentages with a range of 0% to 100%.
According to the given information:The probability of getting at least 2 fours is the sum of the probabilities of getting exactly 2, 3, 4, or 5 fours:
P(X ≥ 2) = P(X=2) + P(X=3) + P(X=4) + P(X=5)
Using the binomial formula, we can calculate each of these probabilities:
P(X=k) = (n choose k) p^k (1-p)^(n-k)
where (n choose k) is the binomial coefficient, which represents the number of ways to choose k items from n distinct items.
P(X=2) = (5 choose 2) (1/6)² (5/6)³ = 0.1608
P(X=3) = (5 choose 3) (1/6)³ (5/6)² = 0.0322
P(X=4) = (5 choose 4) (1/6)⁴ (5/6)¹ = 0.0013
P(X=5) = (5 choose 5) (1/6)⁵ (5/6)⁰ = 0.00003
Therefore,
P(X ≥ 2) = 0.1608 + 0.0322 + 0.0013 + 0.00003 = 0.1943
So the probability, rounded to the nearest thousandth, of getting at least 2 fours in 5 rolls of a fair die is 0.194.
To know more about probability visit:
https://brainly.com/question/12431044
#SPJ1
Given that Tris has a pKa of 8.07, for how many of the experiments would Tris have been an acceptable buffer?
Answers
Tris would be an acceptable buffer for 1 experiment out of every 10⁹ experiments at pH 8.07, assuming a required buffer capacity of 10⁻⁵M.
To determine if Tris would be an acceptable buffer for an experiment, we need to calculate the buffer capacity (β) of Tris at the desired pH range of the experiment. The buffer capacity is given by:
β = βmax x [Tris]/([Tris] + K)
where βmax is the maximum buffer capacity, [Tris] is the concentration of Tris, K is the acid dissociation constant (Ka), and [] denotes the concentration of the species in solution.
At the pH range where Tris is an effective buffer, the pH should be close to the pKa value.
Let's assume that we want to use Tris to buffer a solution at pH 8.07. At this pH, the concentration of the protonated form of Tris ([HTris]) should be equal to the concentration of the deprotonated form ([Tris-]).
So, the acid and conjugate base forms of Tris are present in equal amounts:
[HTris] = [Tris-]
We can also express the equilibrium constant for the reaction as:
K = [H+][Tris-]/[HTris]
Substituting [HTris] = [Tris-], we get:
K = [H+]
At pH 8.07, the concentration of H+ is:
[H+] = \(10^{(-pH)\) = \(10^{(-8.07)\)= 7.08 x 10⁻⁹ M
Now we can calculate the buffer capacity of Tris at this pH. The maximum buffer capacity of Tris occurs when [Tris] = K, which is:
βmax = [Tris]/4
β = (K/4) x [Tris-]/([Tris-] + K)
β = (K/4) x (0.5) = K/8
β =\(10^{(-8.07)\)/8 = 1.72 x 10⁻⁹ M
Comparing this value to the buffer capacity of Tris calculated above, we can see that Tris would be an effective buffer for pH 8.07 in the following experiments:
1.72 x 10⁻⁹ M x 10⁹
= 1.72
Therefore, Tris would be an acceptable buffer for 1 experiment out of every 10⁹ experiments at pH 8.07, assuming a required buffer capacity of 10⁻⁵M.
Learn more about Buffer capacity here:
https://brainly.com/question/491693
#SPJ1
Plz help with this problem

Answers
Answer:
A = 222 in²
Step-by-step explanation:
A = 2(wl+hl+hw) Use this equation to find the surface area of the rectangular prism
A = 2(5*12 + 3*12 + 3*5) Multiply
A = 2(60 + 36 + 15) Add in the parentheses
A = 2(111) Multiply
A = 222 in²
If this answer is correct, please make me Brainliest!
YEAR 9 MATHS PLEASE HELP ME
The pictures are in order - first being dwayne's and second being ivor's Dwayne Pipes uses this formula to work out the cost of a plumbing job in pounds.
Ivor Wrench uses this formula to work out the cost of a plumbing job in pounds. A job of x hours costs the same with Dwayne and Ivor.
Set up and solve an equation to work out x .
X=.........


Answers
The solution is: x = 10/3 hours
What is the equations with one variable?
An equation with one variable is a mathematical statement that involves an unknown quantity represented by a letter, usually x, and an equal sign, where the expressions on both sides of the equal sign have the same value.
We need to set up an equation using the given information to solve for x.
Let's start with Dwayne's formula:
Cost = 30x + 50
And Ivor's formula:
Cost = 45x
Since a job of x hours costs the same for both Dwayne and Ivor, we can set their formulas equal to each other:
30x + 50 = 45x
Simplifying and solving for x:
50 = 15x
x = 50/15
x = 10/3 hours
Therefore, the solution is: x = 10/3 hours
To learn more about equations with one variable, Visit
https://brainly.com/question/85774
#SPJ1