sin^-1(1/2)
Please help I don't know how to do inverse or arcs
Thanks
Answers
Answer:
pi/6
Step-by-step explanation:
An inverse sin is asking which point on the unit circle has that value as its sin
Which in this case, is pi/6
\((\frac{\sqrt{3} }{2} ,\frac{1}{2}) \)
Hope this helps
Answer:
pi/6
Step-by-step explanation:
Arcsin of 1/2 is pi/6
Give me brainliest
Related Questions
consider a two-factor factorial design with three levels for facts a, three levels for factor b, and four replicates in each of the nine cells
a. how many degrees of freedom are there in determining the A variation and the factor B variation
b. how many degrees of freedom are there in dreaming the interaction variation
c. how many degrees of freedom are there in determining the random variation
d. how many degrees of freedom are there in determining the total variation
Answers
In calculating the factor A variation, there are two degrees of freedom. In determining the variation of factor B, there are two degrees of freedom.
What is a two-factorial design?A two-factor factorial design is an experiment that collects data for all potential values of the two factors of the study. The design is a balanced two-factor factorial design if equivalent sample sizes are used for every of the possible factor combinations.
Suppose we have two components, A and B, each of which has a high number of levels of interest. We will select a random level of component A and a random level of factor B, and n observations will be taken for each experimental combination.
From the data given:
a.
In calculating the factor A variation, there are two degrees of freedom.
In determining the variation of factor B, there are two degrees of freedom.
b.
Finding the degree of freedom using the interaction variation, there are four degrees of freedom.
c.
In finding the random variable, there are 9(4-1) = 27 degrees of freedom.
d.
In calculating the total variable, there are 9*4-1 =35 degrees of freedom.
Learn more about using a two-factor factorial design for determining the degree of freedom here:
https://brainly.com/question/14292694
#SPJ1
Which of the following are solutions to the equation below? Check all that apply. x2 + 10x + 25 = 2
Answers
Answer:
-5+√2 and -5-√2
Step-by-step explanation:
With the quadratic formula:
\(\displaystyle x^2 + 10x + 25 = 2\\\\x^2+10x+23=0\\\\x=\frac{-10\pm\sqrt{10^2-4(1)(23)}}{2(1)}=\frac{-10\pm\sqrt{100-92}}{2}=\frac{-10\pm\sqrt{8}}{2}=\frac{-10\pm2\sqrt{2}}{2}=-5\pm\sqrt{2}\)
We can also complete the square (which is faster):
\(x^2+10x+25=2\\(x+5)^2=2\\x+5=\pm\sqrt{2}\\x=-5\pm\sqrt{2}\)
c) If you invest $5800 in a bank that gives you 13% interest compounded quarterly, how much do you
have at the end of the year?
Answers
Answer:
$8,062
Step-by-step explanation:
you open the bank account with $5,800. since the interest is calculated by quarter which is 3 months, you take the interest on the $5,800 and multiply the interest rate times 3. so it would be, $5,800 + $754 + 754 + 754 = 8,062. the $754 amount is calculated by multiplying 5,800 dollars * 13% or .13
Solve for x round to the nearest tenth of a degree if necessary. HURRYYYY TY

Answers
The value of x is 58.51 degree.
We have,
Perpendicular= 8
Base = 4.9
Using trigonometry
tan x = Perpendicular/ Base
tan x = 8/4.9
tan x= 1.63265306122449
x = 58.51253064
Thus, the value of x is 58.51 degree.
Learn more about Trigonometry here:
https://brainly.com/question/12068045
#SPJ1
What is the equation of the line in slope intercept form?

Answers
Answer:
y = x + 60
Step-by-step explanation:
the equation of a line in slope- intercept form is
y = mx + c ( m is the slope and c the y- intercept )
calculate m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (20, 80) and (x₂, y₂ ) = (40, 100) ← 2 points on the line
m = \(\frac{100-80}{40-20}\) = \(\frac{20}{20}\) = 1
the line crosses the y- axis at (0, 60 ) ⇒ c = 60
y = x + 60 ← equation of line
The sum of the measures of the angles of any triangle is 180 degrees in triangle ABC angles A and B have the same measure while the measure of angle c is 63 degrees larger than each of A and B
Answers
Answer:
m∠A = 39°
m∠B = 39°
m∠C = 102°
Step-by-step explanation:
m∠A + m∠B + m∠C = 180°
x + x + (x + 63) = 180
3x + 63 = 180
3x = 117
x = 39°
m∠A = 39°
m∠B = 39°
m∠C = m∠A + 63 = 39 + 63 = 102°
Answer:
39 39 102
Step-by-step explanation:
Lydia made some cookies, of which 1/3 were chocolate chip, ¾ of the remainder were gingersnaps and the rest were peanut butter. If Lydia made 4 dozen cookies altogether, how many peanut butter cookies did she make?
I mark brainliest by today
Answers
Answer:
8 peanut cookies
Step-by-step explanation:
4 x 12 = 48
48 x 1/3 = 2/3 left (16 chocolate chip)
48-16= 2/3 = 32 left
32 x 3/4 = 24 (24 gingersnaps)
32-24 = 8 ( 8 peanut cookies)
Graph a line that is parallel to the line x=4 that goes through the point (−2,3)
Answers
{REPOST: FORGOT TO INCLUDE PICTURE FOR QUESTION 10}
{Question 10} Please help, need this by tonight! Thanks so much :) {Click on picture}

Answers
Answer:
X-intercept: (6, 0)
Y-intercept: (0, -9)
Step-by-step explanation:
Required: Find the X and Y intercept of the standard from equation:
-3x + 2y = -18.
We shall write equation in the form \(\frac{x}{a} +\frac{y}{b} =1\) and find the intercepts on X and Y axis:
-3x + 2y = -18
∴ -3x + 2y = -18
∴ -3x/-18 + 2y/-18 = 1
∴ x/6 + y/-9 = 1
Comparing this equation with \(\frac{x}{a} +\frac{y}{b} =1\), we get:
intercept of X-axis = a = 6
intercept of Y-axis = b = -9
Thanks.
Answer:
The y-intercept for the line is ( 0, -9 ).
Hope this helps!
Step-by-step explanation:
The y-intercept is where the graph intercepts the y-axis and is the y-value of the point, ( x, y ).

4. Katy has 6 times as many nickels as
Shaun. Shaun has 18 nickels. How many
nickels, n, does Katy have?
n is 6
18.
n=
Answers
Answer:
\(\huge\boxed{n = 108\ nickels}\)
Step-by-step explanation:
Let the nickels with Katy be n
So, the condition is
n = 6 (Shaun nickels)
While Nickels of Shaun = 18 , So
n = 6 (18)
n = 108 nickels
Write each parabola in the form y−k=a(x−h)^2 and determine its vertex: y=−4x^2+16x−19
Answers
-16/2(-4) = 2
Substitute 2 into the equation
Y = -4(2)^2 + 16(2) - 19
Y = -16 + 32 - 19 = -3
Vertex = (2, -3)
Vertex form y+3=-4(x-2)^2
What is the answer of this triangle congruence question.

Answers
The value of x in the triangles are 9.
What is a quadratic equation?For variable x : ax² + bx + c = 0, where a≠0 is a standard quadratic equation, which is a second-order polynomial equation in a single variable. It has at least one solution since it is a second-order polynomial equation, which is guaranteed by the algebraic basic theorem.
Given:
The triangles are congruent.
That means, their corresponding angles are also congruent.
In ΔJKL,
the sum of all the angles of the triangle is 180°.
So,
x²-2x + x + 29 + 3x + 52 = 180
x² + 2x - 99 = 0
Solving the quadratic equation,
x² +11x - 9x - 99 = 0.
x (x + 11) -9 (x + 11) = 0
x = 9 and x = -11
Here, we take x = 9.
Therefore, the value of x is 9.
To learn more about the quadratic equation;
https://brainly.com/question/17177510
#SPJ1
Use the formula P = 2l + 2w to find the length l of a rectangular lot if the width w is 55 feet and the perimeter P is 260 feet.l = ? feet
Answers
In order to determine the length of the given rectangle, Solve the equation for the perimeter of the rectangle for l and replace w=55ft and P=260ft, and simplify:
\(\begin{gathered} P=2l+2w \\ 2l=P-2w \\ l=\frac{P-2w}{2} \\ l=\frac{260ft-2(55ft)}{2} \\ l=\frac{260ft-110ft}{2} \\ l=\frac{150ft}{2}=75ft \end{gathered}\)Hence, the length of the rectangle is 75ft
You pick a card at random. 5 6 7 What is P(odd or greater than 6)?
Answers
The answer to the question is 1/3.
There are three possible outcomes: 5, 6, or 7.
Out of these three outcomes, only two satisfy the condition of being odd or greater than 6: 7.
Therefore, the probability of picking a card that is odd or greater than 6 is 1/3, or approximately 0.333 or 33.3%.
To solve more on probability :
https://brainly.com/question/12594357?referrer=searchResults
12.
The ratio of boys to girls in a class is 3:7. Write down the fraction of the class who are boys.
Answers
Answer:
let tle number of boys and girls be 2x and3x
Step-by-step explanation:
like this solve the question
For the point P(6,8) and Q(11,11), find the distance d(P,Q) and the coordinates of the
midpoint M of the segment PO.
What is the distance?
(Simplify your answer. Type an exact answer, using radicals as need.)
Answers
Answer:
The distance of PQ = \(\sqrt{34}\)
Step-by-step explanation:
Explanation:-
Given that the points are P(6,8) and Q(11,11)
Distance formula
PQ = \(\sqrt{x_{2}-x_{1} )^{2} +(y_{2} - y_{1})^{2} }\)
= \(\sqrt{11-6)^{2} +(11-8)^{2} }\)
= \(\sqrt{(5)^{2}+(3)^{2}} }\)
= \(\sqrt{25+9}\)
= \(\sqrt{34}\)
1. Global warming creates local problems. Projections forecast that even a moderate air temperature increase of only 1.8 °F could cause brook trout distributions to decrease dramatically. For example, such a temperature increase would take Washburn county's 19 ponds that support brook trout down to 10 ponds. What would be the percent decrease in the number of ponds that support brook trout?
Answers
The percent decrease in the number of ponds that support brook trout would be approximately 47.37%.
To calculate the percent decrease in the number of ponds that support brook trout, we need to determine the difference between the initial number of ponds and the final number of ponds, and then express that difference as a percentage of the initial number of ponds.
Initial number of ponds: 19
Final number of ponds: 10
To calculate the percent decrease, we can use the following formula:
Percent Decrease = (Difference / Initial Value) * 100
Let's apply this formula to the given data:
Difference = Initial number of ponds - Final number of ponds
Difference = 19 - 10
Difference = 9
Percent Decrease = (9 / 19) * 100
Now, let's calculate the percent decrease:
Percent Decrease = (9 / 19) * 100
Percent Decrease ≈ 47.37%
For such more question on number:
https://brainly.com/question/30752681
#SPJ8
Multiple choice: Select the best answer for Exercises 49 to 52. Most people can roll their tongues, but many can’t. The ability to roll the tongue is genetically determined. Suppose we are interested in determining what proportion of students can roll their tongues. We test a simple random sample of 400 students and find that 317 can roll their tongues. The margin of error for a 95% confidence interval for the true proportion of tongue rollers among students is closest to (a) 0.008. (b) 0.02. (c) 0.03. (d) 0.04. (e) 0.208.
Answers
The margin of error for a 95% confidence interval for the true proportion of tongue rollers among students is closest to (d) 0.04
The margin of error is a statistic that describes how much random sampling error there is in survey results.
Given in question,
n = 400
p = 317/400
= 0.7925
Confidence Level = 95%
= 0.95
Formula for margin error, E = \(z\sqrt{\frac{p(1-p)}{n} }\)
Confidence level corresponding to 95 % confidence interval, z = 1.96
Therefore,
Margin Error, E = \(1.96\sqrt{\frac{0.7925(1-0.7625)}{400} }\)
= 0.0397
≈ 0.04
Hence, The margin of error for a 95% confidence interval for the true proportion of tongue rollers among students is 0.0397 which is closest to 0.04.
To learn more about margin of error here:
https://brainly.com/question/10501147
#SPJ4
Determine the value of x.
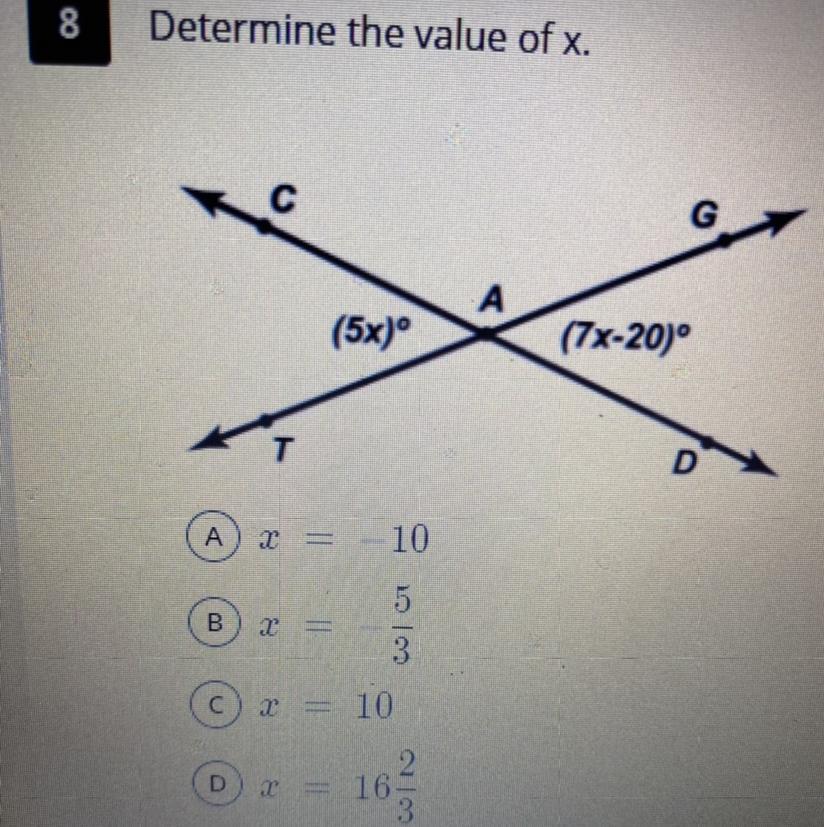
Answers
Answer:
x=10
Giving brainiest would be appreciated! :D
What is the following sum?
5(³3√x)+9(³√x)
0 14 (√x)
14 (2√x²)
0 14 (3√x)
0
X
Answers
The solution for the given expression is 14∛x. The correct option is (C).
What is an Algebraic expression?An algebraic expression can be obtained by doing mathematical operations on the variable and constant terms.
The variable part of an algebraic expression can never be added or subtracted from the constant part.
The given expression is as below,
5∛x + 9∛x
The given expression can be simplified as follows,
5∛x + 9∛x
Here, both the terms have equivalent variables. So, both are like terms.
As per the rules like terms can be added or subtracted keeping the variable as the same.
Thus, 5∛x + 9∛x = 14∛x
Hence, the given expression can be evaluated as 5∛x + 9∛x = 14∛x.
To know more about algebraic expression click on,
brainly.com/question/953809
#SPJ1
A wire that is 76 feet long needs to be divided into lengths using the ratio 1 to 13. What is the longer length? Round your answer to two decimal places if necessary.
Answers
Answer:
70.59 feet
Step-by-step explanation:
There are a total of 14 parts when the wire is divided into a ratio of 1 to 13.
1. Divide 76 by 14
76 ÷ 14 = 5.43
2. Multiply the longer length of 13 parts
5.43 · 13 = 70.59
The longer length of the wire 70.59 feet
There are a total of 14 parts when the wire is divided into a ratio of 1 to 13.
1. Divide 76 by 14
76 ÷ 14 = 5.43
2. Multiply the longer length of 13 parts
5.43 · 13 = 70.59
What is a decimal in numbers?In algebra, a decimal number can be defined as a range whose entire number part and the fractional element are separated by means of a decimal point. The dot in a decimal range is referred to as a decimal point. The digits following the decimal factor show a price smaller than one.
Learn more about Algebra here https://brainly.com/question/723406
#SPJ2
2a+c=162.97
how do you use the elimination method for this
Answers
When 'a' is 10, 'c' is approximately 142.97. You can repeat this process for different values of 'a' to find corresponding values of 'c'. Keep in mind that there are infinitely many solutions to this equation
To use the elimination method to solve the equation 2a + c = 162.97, we need another equation with the same variables. However, as there is only one equation given, we cannot apply the elimination method directly.
The elimination method typically involves adding or subtracting equations to eliminate one of the variables, resulting in a new equation with only one variable. Since we have only one equation, we don't have the opportunity to eliminate variables using another equation.
In this case, we can solve the given equation directly by isolating one variable in terms of the other. Let's solve for 'c':
2a + c = 162.97
Rearrange the equation to isolate 'c':
c = 162.97 - 2a
Now, we have an expression for 'c' in terms of 'a'. This equation represents a line in the 'a-c' coordinate plane. We can choose any value for 'a', substitute it into the equation, and calculate the corresponding 'c' value.
For example, let's say we choose 'a' = 10:
c = 162.97 - 2(10)
c = 162.97 - 20
c = 142.97
So, when 'a' is 10, 'c' is approximately 142.97.
You can repeat this process for different values of 'a' to find corresponding values of 'c'. Keep in mind that there are infinitely many solutions to this equation since we have one equation and two variables.
for more such question on corresponding visit
https://brainly.com/question/11853802
#SPJ8
c) If f(3x + 4)=5x + 8, find f '(x) and f(3)
Answers
Answer:
f(3x + 4) = 5x + 8
⇔ f(3x + 4) = \(\frac{5}{3}(3x+\frac{24}{5})\)
⇔ f(3x + 4) = \(\frac{5}{3}(3x+4+\frac{4}{5})\)
⇒ f'(x) = \(\frac{5}{3}(x+\frac{4}{5})\)
=> f(3) = \(\frac{5}{3}(3+\frac{4}{5})= \frac{19}{3}\)
Step-by-step explanation:
An oil tank has to be drained for maintenance. The tank is shaped like a cylinder that is 3 ft long with a diameter of 1.8 ft. Suppose oil is drained at a rate of 1.7 ft³ per minute. If the tank starts completely full, how many minutes will it take to empty the tank? Use the value 3.14 for pi, and round your answer to the nearest minute. Do not round any intermediate computations.
Answers
Answer:
4 minutes
Step-by-step explanation:
You want to know how long it takes to drain a cylindrical tank 1.8 ft in diameter and 3 ft long at the rate of 1.7 ft³/minute. (π = 3.14)
VolumeThe volume of a cylinder can be found using the formula ...
V = (π/4)d²h . . . . . . . diameter d, height h
Then the volume of the oil tank is ...
V = 3.14/4(1.8 ft)²(3 fft) = 7.6302 ft³
TimeThe time it takes to empty the tank is found by dividing the volume by the rate:
(7.6302 ft³)/(1.7 ft³/min) ≈ 4.49 min ≈ 4 min
It will take about 4 minutes to empty the tank.
<95141404393>

❗️❗️❗️Find the length of side x in simplest radical form with a rational denominator.❗️❗️❗️
Plzzz helppp meeee

Answers
Answer:
\(x=\frac{\sqrt{14} }{2}\)
Step-by-step explanation:
Notice that you are given an isosceles right-angle triangle to solve, since each of its two acute angles measures \(45^o\). Then such means that the sides opposite to these acute angles (the so called "legs" of this right angle triangle) must also be of the same length (x).
We can then use the Pythagorean theorem that relates the square of the hypotenuse to the addition of the squares of the triangles legs:
\((\sqrt{7})^2=x^2+x^2\\7=2\,x^2\\x^2=\frac{7}{2} \\x=+/-\sqrt{\frac{7}{2}} \\x=+/-\frac{\sqrt{14} }{2}\)
We use just the positive root, since we are looking for an actual length. then, the requested side is:
\(x=\frac{\sqrt{14} }{2}\)
Where is the velocity positive?
x
C D
E
B
t
A А
A. B-E
B. C-D
C. A-C
D. B & E

Answers
Answer: C
Step-by-step explanation:
Given
Displacement vs time graph is shown with Point from A to G
from A to C displacement increases with time such that the slope of the x-t graph is positive
from C to D it is almost zero; from D to F it is negative
Also, slope of x-t graph is velocity
Thus, the positive velocity is seen in A to C
Evaluate
(y + z)^2when y = -8, z =19
Answers
Answer:
Substitute the value of the variable into the expression and simplify.
121
Step-by-step explanation:
Step-by-step explanation:
(y + z)^2
substitute in the given
y = -8, z = 19
(-8 + 19)^2
(11)^2
121
Hope this helps :)
Max delivers 9,360 pieces of mail in one year. About how many pieces of mail does he deliver in 4 months?
Answers
Answer:
3,120 in 4 months
Step-by-step explanation:
9,360 divided by 12 = 780
780 x 4 = 3,120
can someone help me with this

Answers
The sine equation for the object's height is given as follows:
d = -5sin(0.24t).
How to define the sine function?The standard definition of the sine function is given as follows:
y = Asin(Bx) + C.
The parameters are given as follows:
A: amplitude.B: the period is 2π/B.C: vertical shift.The amplitude for this problem is of 5 inches, hence:
A = 5.
The period is of 1.5 seconds, hence the coefficient B is given as follows:
2π/B = 1.5
B = 1.5/2π
B = 0.24.
The function starts moving down, hence it is negative, so:
d = -5sin(0.24t).
More can be learned about trigonometric functions at brainly.com/question/21558626
#SPJ1
You are playing in the NBA Playoffs and attempt a 3-point shot as the buzzer sounds for the end of the
game, if you make the shot your team wins! Your basketball is is traveling on a path described by the
following function: b(x) = -x2 +1.36x + 2. The net is on a level described by the following function:
n(x) = 3 between (8 < x < 8.5). Will you make the shot and win the playoffs?
You may work alone or in a group of up to 3 students total.
BONUS: How high in the air will the basketball be at its highest point?
UNITS: x is in meters, y is in meters

Answers
Since we do not know the value of u, we cannot find the time taken by the basketball to travel a distance of 8.5 meters. We cannot find the height of the basketball at its highest point.
Given that n(x) = 3 for 8 < x < 8.5.It is impossible to determine whether the shot will be made or not based solely on this information. Winning the playoffs depends on various factors, such as the score, time remaining, and the overall performance of the team.
Therefore, additional information is required to determine the outcome of the playoffs.However, to find the height of the basketball at its highest point, we need to know the equation of the trajectory of the basketball.
Assuming that the basketball follows a parabolic path, we can use the formula:
y = ax² + bx + c,
where y is the height of the basketball, and x is the horizontal distance traveled by the basketball.
To find the values of a, b, and c, we need to know three points on the trajectory of the basketball. Let's assume that the basketball is thrown from a height of 1.5 meters and lands on the floor after traveling a horizontal distance of 8.5 meters.
Therefore, the points on the trajectory of the basketball are:
(0, 1.5), (8.5/2, h), and (8.5, 0),
where h is the height of the basketball at its highest point.Substituting these values in the equation of the trajectory,
we get:
1.5 = a(0)² + b(0) + c...(1)0 = a(8.5)² + b(8.5) + c...(2)h = a(8.5/2)² + b(8.5/2) + c...(3)
Simplifying equations (1) and (2),
we get:
c = 1.5...(4)b = -a(8.5)²/8.5...(5)
Substituting equation (4) in equation (3), we get:
h = a(8.5/2)² + b(8.5/2) + 1.5h = a(8.5/2)² - a(8.5)²/8.5 + 1.5h = -29.375a + 1.5
Substituting the value of a from equation (5) in the above equation,
we get:
h = -29.375(-a(8.5)²/8.5) + 1.5h = 0.5a(8.5)² + 1.5
Therefore, to find the height of the basketball at its highest point, we need to find the value of a. Since we know that the basketball lands on the floor after traveling a horizontal distance of 8.5 meters,
we can use the formula:
x = ut + 0.5at²,
where u is the initial horizontal velocity of the basketball, and t is the time taken by the basketball to travel a distance of 8.5 meters.
To learn more about : time
https://brainly.com/question/26862717
#SPJ8